基于梯度下降优化的LSTM对空气质量预测研究

曹 通， 白艳萍

(中北大学 理学院, 山西 太原 030051)

0 引言

目前，深度学习是人工智能应用方面较为活跃的一个研究分支，也是一类更加广泛的机器学习方法，它是用很多交互层构成的求解器来训练兼具多个具象级的相关统计数据，宗旨在于研究其媒介特性，同时可用于发掘模型并实现预测[1,2].针对空气质量易受气候因素、大气污染物的影响，同时具有显著的不确定性和非线性的特征[3]，以人工神经网络为代表的深度学习是目前国内外空气质量预测领域最为流行的研究方法.

早在20世纪90年代，人工神经网络理论就被一些专家学者应用到空气污染物浓度预测中，空气质量预测研究开始踏入一段新的历程.随即在1997年，Horchreater和Schmidhuber首次提出了长短期循环时间网络.现如今也已经被运用到了空气质量预测中，因为它建立预测模型的方式是数据驱动，无需繁琐的逻辑推演，只需要收集到以往的污染物浓度相关数据即可.

目前，这些系统的一个主要研究问题是通过优化算法的训练来提高此模型的预测精度.本文尝试着结合随机梯度下降算法内存需求小、不易陷入局部最优解、更新频率快的优点，提出了基于Adagrad、AdaDelta、Adam三种随机梯度下降算法优化的LSTM预测模型.通过对网络结构层中的权重参数和偏差项进行修正[4]，从而提升LSTM模型的预测精度.最后以太原市真实空气质量数据进行仿真实验，对比实验结果验证了Adam优化算法的优越性.

1 LSTM循环神经网络

LSTM循环神经网络(Long Short Term Memory)[5]是一种特殊的RNNs，它针对RNN在深度学习中易陷入梯度消失和爆炸的问题，在隐含层各神经单元处理层中增添了存储单元和门控制机制，此外也更加易于训练，适用于预测和处理间隔和延迟比较长的相关事件.它是由一序列循环连接的记忆模块所构成，其中每个里面都有一个或多个自连接的神经元和三个控制各类信息传播门限系统单元，分别为：输入门、输出门和遗忘门[6-8]，具体如图1所示.

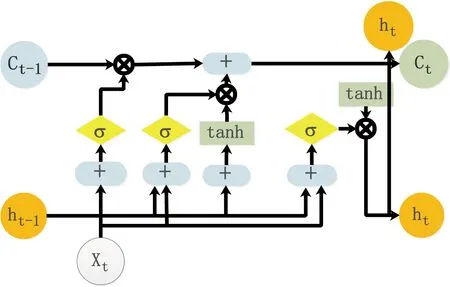
图1 LSTM流程图

在LSTM网络结构层中，其运行步骤如下：

(1)遗忘门：主要用于计算信息的保留和丢弃程度，通过sigmoid处理后为0-1的值，1代表上级信息全部保留，0代表全部丢弃，公式如下：

f(t)=σ(Wfh(t-1)+Ufx(t)+bf)

(1)

式(1)中：Wf,Uf则是遗忘门的训练参数，输入为：当前时刻的x(t)和上一时刻隐含层的输出h(t-1)，σ为sigmoid函数.

(2)输入门：用来计算哪些信息保留到下一个状态单元中，主要包括两部分信息，一部分是可以看成当前输入有多少信息需要存储到单元状态，另一部分是通过把当前输入产生的新的信息添加到下一个状态中，而形成新的记忆信息，公式如下：

i(t)=σ(Wix(t)+Uih(t-1))

(2)

(3)

此外，“细胞状态”通道：用来计算Ct-1到Ct，该通道贯穿了整个时间序列，公式如下：

(4)

(3)输出门：用于计算当前时刻信息被输出的程度，公式如下：

o(t)=σ(Wox(t)+Uoh(t-1))

h(t)=o(t)·tanh(c(t))

(5)

2 自适应调节学习率的随机梯度下降算法

梯度下降[9-11]有着三种不同的形式：批量梯度下降(Batch Gradient Descent),随机梯度下降(Stochastic Gradient Descent),小批量梯度下降(Mini-Batch Gradient Descent).其中随机梯度下降与批量下降不同，它是每次通过使用一个样本迭代来对参数进行更新，进而加快训练速率，在本文中主要研究自适应调节学习率的随机梯度下降优化LSTM神经网络算法.

学习率[12]控制着基于损失函数梯度来调整神经网络的权值参数的速度，如图2所示，是机器学习和深度学习中一个极其重要的超参数.当学习率设置的过小，将会减慢模型的收敛速度；而当学习率设置的过大时，导致梯度可能会在最小值的附近波动，最后无法收敛，如参数更新公式所示：

(6)

在模型训练过程中，通过多轮迭代后，便需要替换一个较小的学习率，目的是减弱波动，进而使优化速率提升，而手动调节学习率不仅消耗人力资源和时间资源，并且快速找出此刻模型环境中的最优值也非常困难.因此，一些学者针对此问题提出了如下几种自适应调节学习率的随机梯度下降算法，且这几种算法在深度神经网络中也表现出了良好的性能，本文选择其中三种算法进行阐述及优化训练，分别为：Adagrad、AdaDelta、Adam.

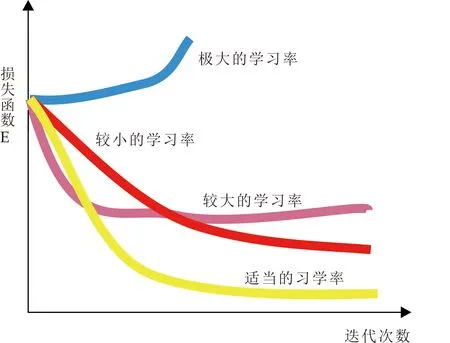
图2 学习率优化影响程度图

为了更加清晰方便地描述三种随机梯度下降算法的核心定理，首先进行符号定义：gt,i=J(θt,i)，gt,i表示θt,i对应的梯度分量；表示的对应的所有梯度分量平方之和；θt,i是在t步之前相应参数分量；ε取值为10-8,目的是避免分母为0.

2.1 Adagrad

Adagrad[13,14]是通过对不同的参数分量进行拆分同时分配不同的学习率，即学习率适应参数变化，可以快速识别出那些低频或者高频、极具预测价值但容易被忽视的特征.

Adagrad算法的更新公式如下：

θt+i=θt+Δθt

(7)

(8)

该算法的提出虽摆脱了手动调节学习率的困扰，但历史梯度平方和无限制的累加，学习率会连续不断地下降，导致模型训练后期的收敛速度会越来越慢.

2.2 AdaDelta

针对Adagrad低效率地对历史梯度平方和累积求和而致使收敛越来越慢的问题，AdaDelta运用了动量因子的平均算法，引入了一个新的概念——“滑动平均”[15]，即用梯度的滑动平均值代替平均值，每轮的梯度的滑动平均值仅依赖于当前时刻梯度的平均值和上一时刻梯度的滑动平均值，并且对累加界限作了约束，AdaDelta算法的更新公式如下：

(9)

(10)

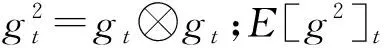
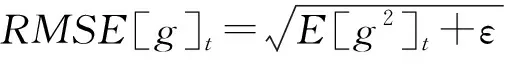
(11)

(12)

式(12)中：RMSE[Δθ]t-1/RMSE[g]t为自适应调节学习率.

2.3 Adam

Adam[16,17]也是一种不同的参数自适应不同的学习速率的方法，它融入了矩估计的思想，并通过计算和校正每轮梯度的一阶矩、二阶矩来实时地调整超参数——学习率，其衰减方式类似动量，如下：

(13)

式(13)中：这些参数取值通常为β1=0.9,β2=0.999,β1，β2∈[0,1)为衰减常数.偏差修正公式为：

(14)

Adam算法的更新公式如下:

(15)

3 实验仿真分析

3.1 模型建立

模型优化思想：众所周知训练神经网络是一种基于称为反向传播的技术，而梯度下降是机器学习中较常使用的优化算法，也是优化神经网络最流行的算法，它主要是通过更新调整神经网络模型的权重来对此进行优化.在训练模型过程中，本文利用反向传播网络的误差，基于梯度下降来更新权重值，也就是说，计算误差函数(E)在权重(W)也就是参数上的梯度，再以损失函数梯度的相反方向来更新权重，如图3所示，U型曲线代表梯度.可得，若权重W值过大或过小，都会产生较大的误差，因此若想要通过更新和优化权重使其既不过小又不过大，可以沿着梯度的反方向下降，直至找到局部极小值.

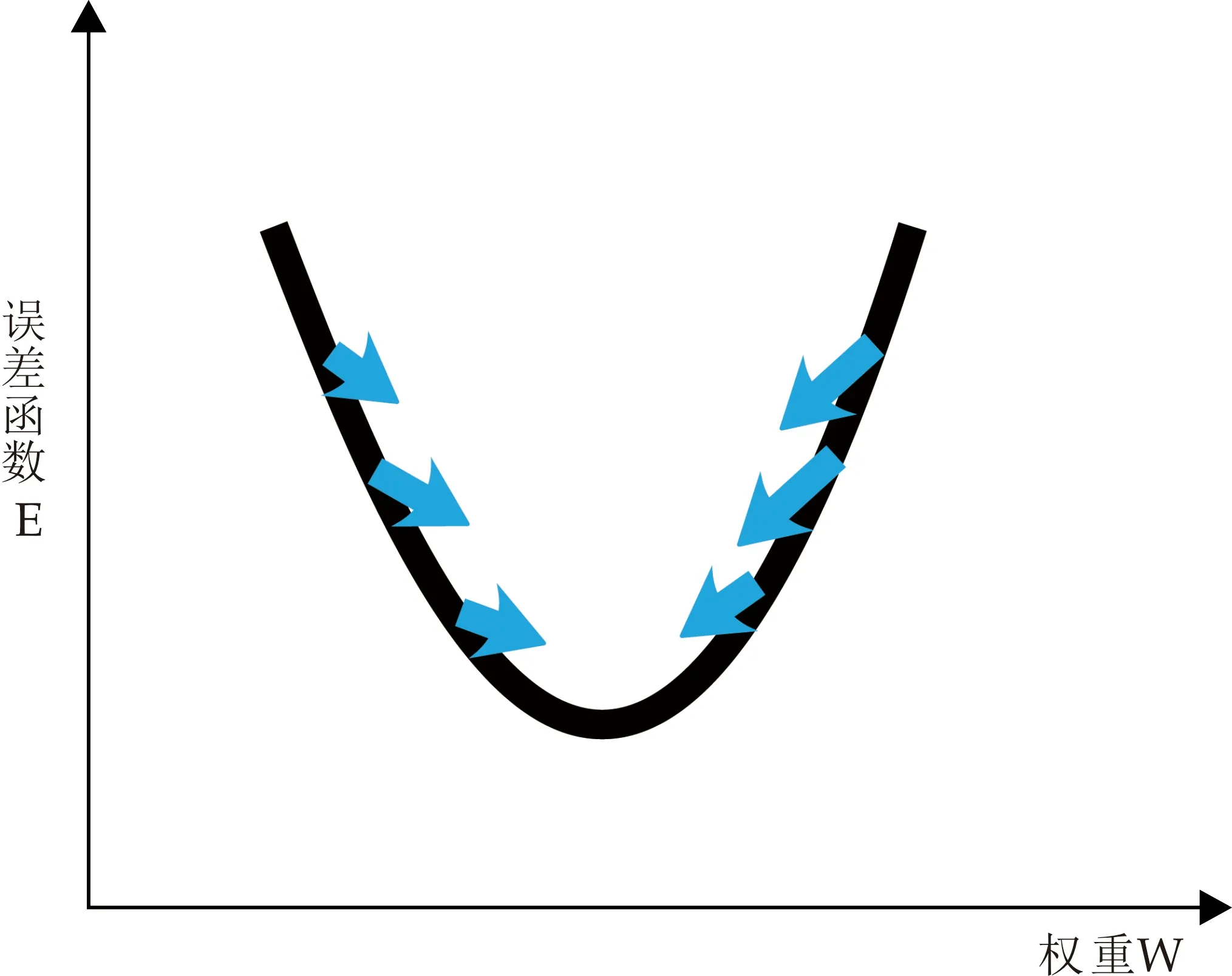
图3 权重与误差函数关系图

在此思路的基础上，经过以下几个步骤设计预测模型，具体如图4所示.

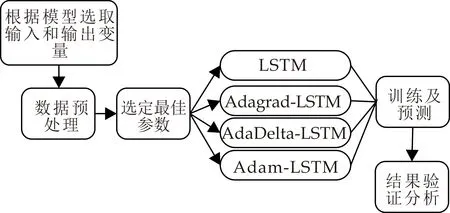
图4 模型建立流程图

3.2 MATLAB实现

本文利用matlab R2014a编程语言来建立太原市LSTM空气质量预测模型，对自适应学习率的随机梯度下降算法在深度学习LSTM神经网络中的性能进行对比.

3.2.1 根据模型选定输入变量和输出变量

此次测试使用的样本数据来源于中国空气质量在线监测分析平台历史数据网(https://www.aqistudy.cn/historydata/)发布的太原市空气质量历史数据，选取的样本数据为太原市2018-01-01～2019-12-31空气污染物数据，共计730组数据，本文将样本分为训练和预测样本，即前620个为测试样本，后110个为预测样本；选取每天的PM2.5、PM10、SO2、CO、NO2、O3、AQI作为输入变量，AQI作为输出变量.

图5为太原市空气质量指数折线图，从图5可以看出AQI数据具有季节性和周期性的特点：冬季12月至次年的3月AQI达到最高；夏季6月至9月AQI值最低.且通过比较AQI和6种污染物指标的变化趋势可知：AQI与PM2.5、PM10、SO2、CO、NO2变化趋势大致相同，而与O3的变化趋势相反.

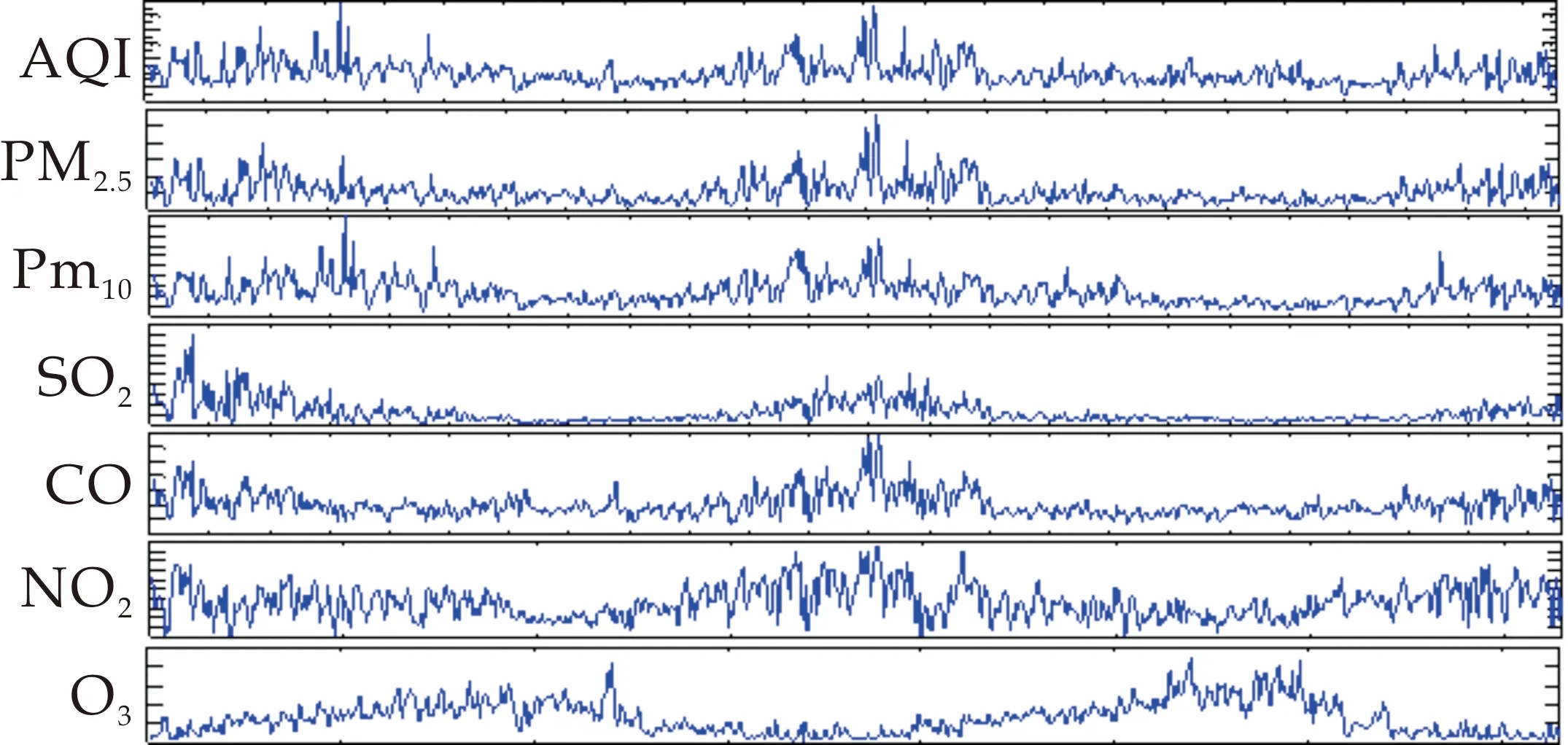
图5 指标变化趋势

3.2.2 数据预处理

通过matlab中的mapminmax函数来完成数据归一化预处理，经过数次仿真实验，预处理效果最好的是以[0,1]区间归一化方式，在此需要阐明的是在本节中不仅要对输出变量(AQI)做归一化处理，对于输入变量也要做相同的预处理.对于每日的AQI数据归一化的结果如图6所示.

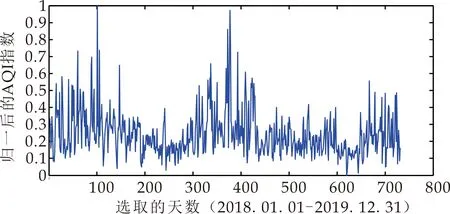
图6 原始空气质量指数归一化的结果图

3.2.3 参数选择

根据相关文献中推荐的三种优化算法的参数，具体如表1所示.

表1 优化算法参数表

3.2.4 训练及预测

利用上面预处理后的数据和选取的最佳参数，通过自适应调节学习率的随机梯度下降优化算法(Adagrad、AdaDelta、Adam)训练LSTM循环神经网络进行预测，再分别用三种预测结果和测试集数据对比，得出用来评估模型精确度的相对误差.最终预测结果和相对误差如图7所示.

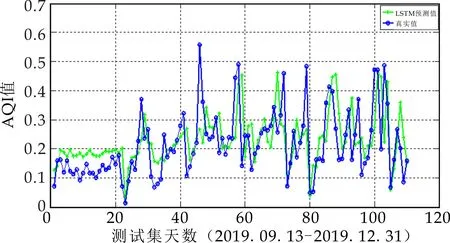
(a)LSTM

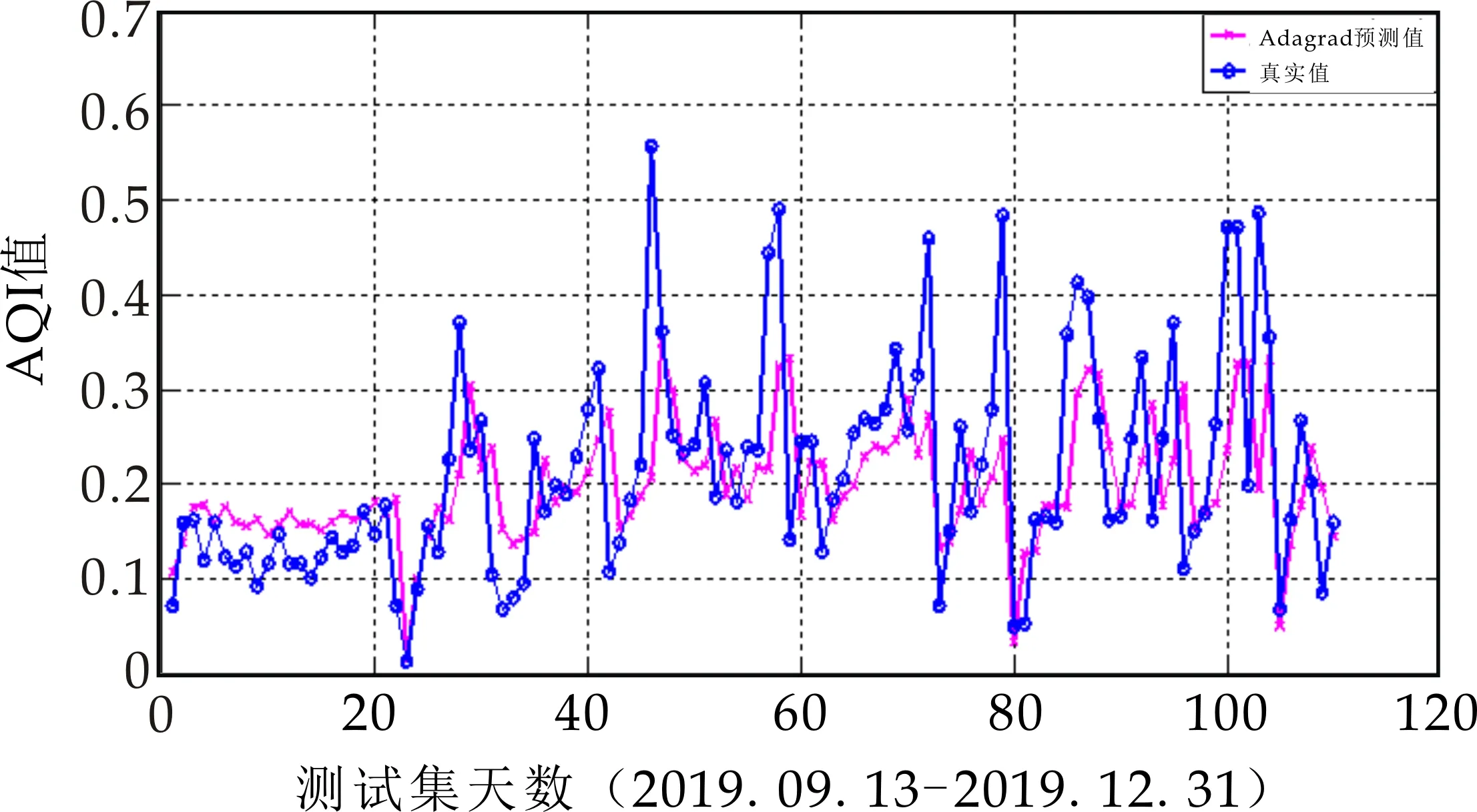
(b)Adagrad

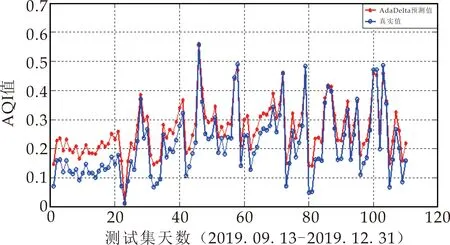
(c)AdaDelta

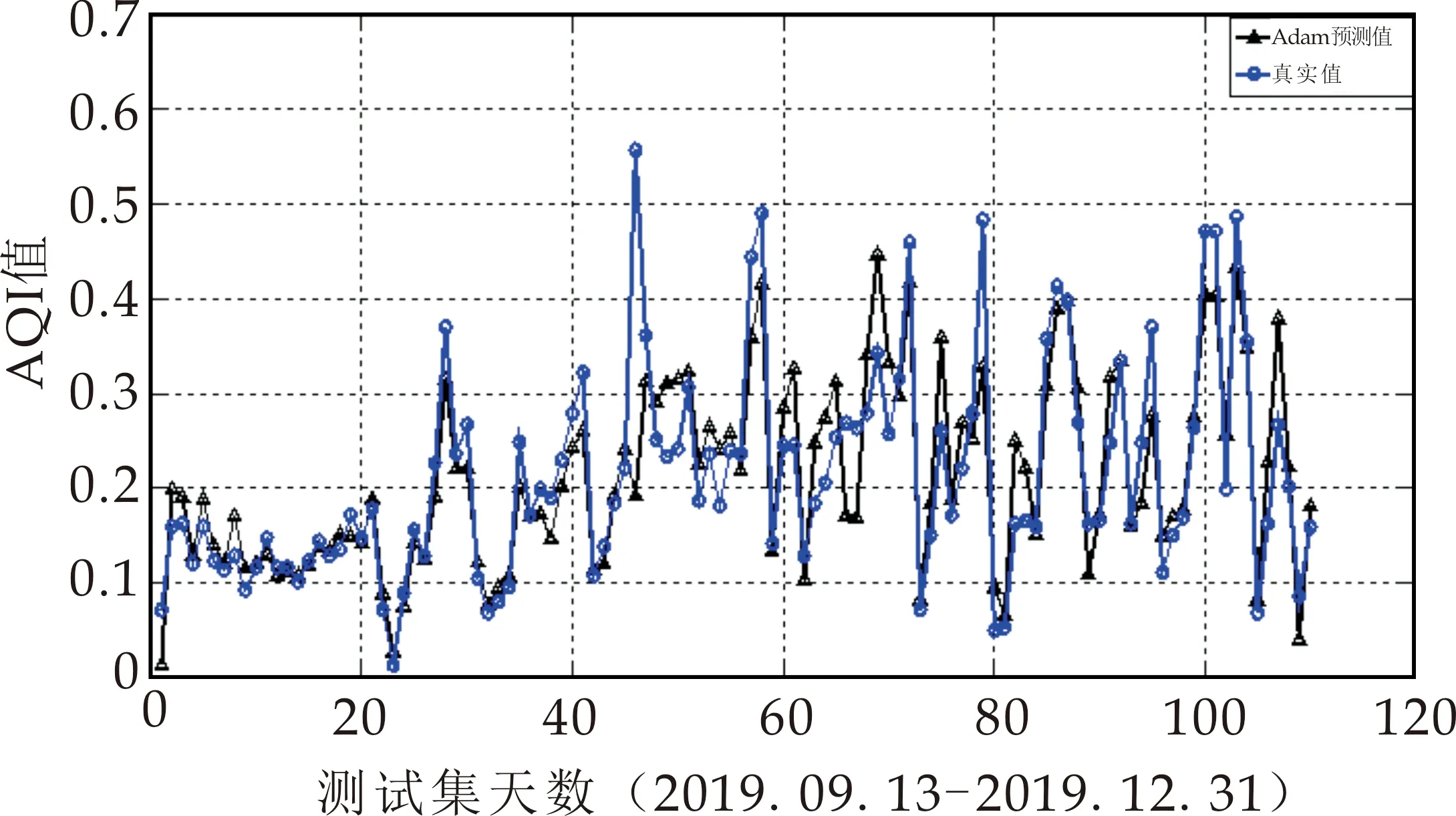
(d)Adam图7 四种模型预测结果图

在图8比较了4种自适应学习率的梯度下降算法优化的LSTM的预测结果，其中：横坐标表示测试集天数，纵坐标表示AQI数值；图9是四种预测结果的相对误差对比图，横坐标为测试集天数，纵坐标为相对误差量.从图8和图9可以看出，Adagrad虽然摆脱了手动调节学习率的困扰，但优化性能最差，导致最差的原因可能为该算法在训练过程中对历史梯度平方和的无节制的累加，学习率持续不断地下降，导致模型的收敛速度也越来越慢，无法突破局部最优点；而AdaDelta优化性能优于Adagrad算法，说明针对Adagrad低效率的问题，AdaDelta引入新的统计量“衰减平均”，对累加范围作限制，其改进效果显著；Adam优化性能最佳，也说明了该算法中的矩估计思想和动量衰减方式，对随机梯度下降算法性能有非常好的改进作用.

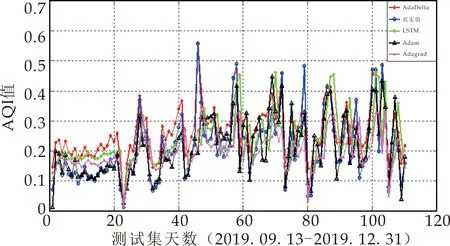
图8 预测结果对比图

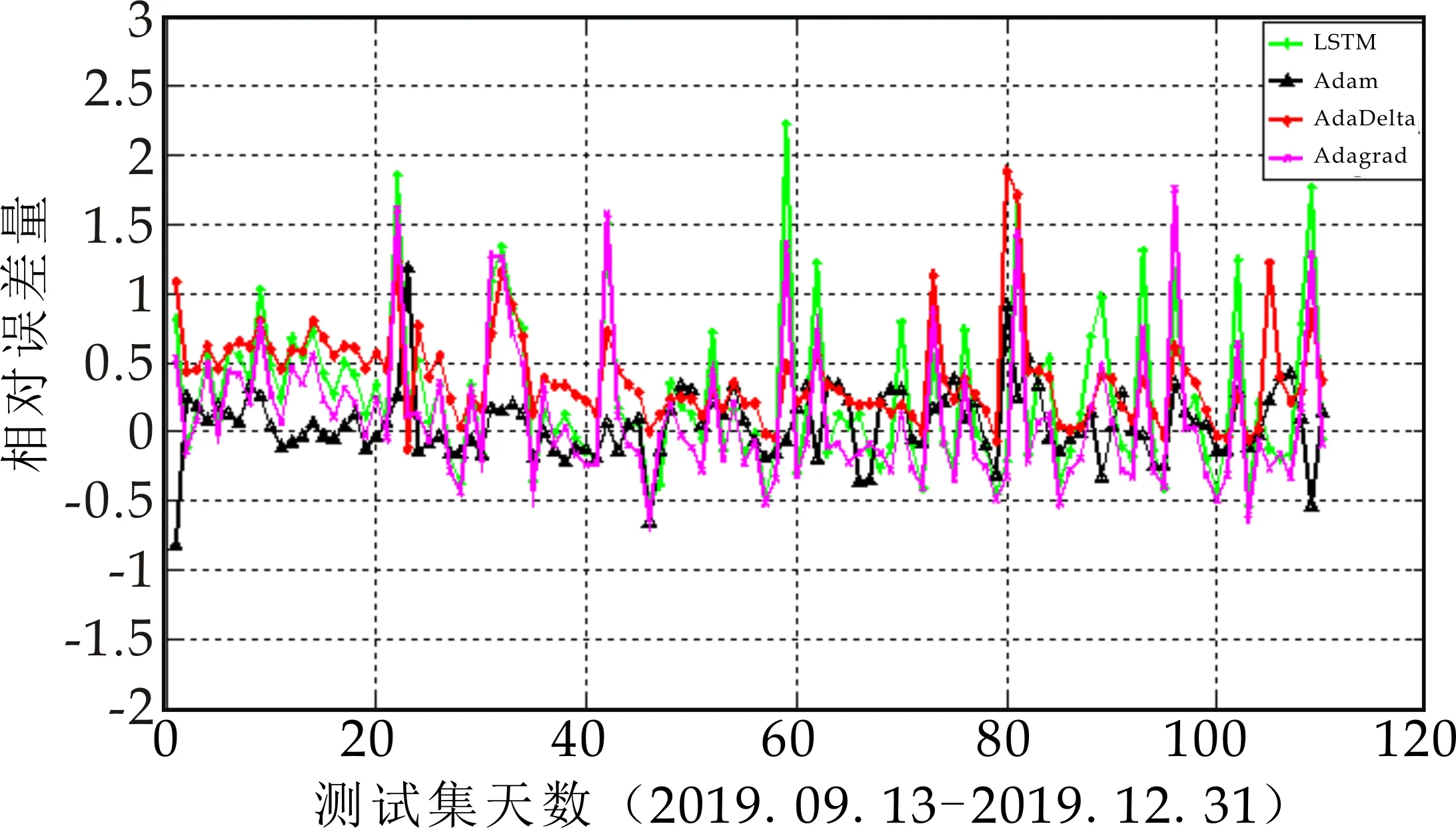
图9 相对误差对比图

表2列出了4种模型的预测误差.平均相对误差MAPE和均方根误差RMSE是国际上两种通用的误差评价指标，前者表示样本数据离散程度，后者表示预测的精度值.通过4种算法的MAPE和RMSE对比，可以验证其算法模型实际性能的优劣程度：单个的LSTM模型的MAPE(13.224 2%)和RMSE(0.240 7)的值都是最高的，表明其预测性能最差；而Adam的MAPE(3.79%)和RMSE(0.004 8)都低于AdaDelta-LSTM的MAPE(4.007 8%)和RMSE(0.005 6)和Adagrad-LSTM的MAPE(7.102 7%)和RMSE(0.055 2)，说明其预测精度最高.可证得：三种随机梯度下降算法都提高了LSTM神经网络模型的预测精度，且Adam优化算法下的深度神经网络LSTM预测模型性能优于其它两种方法.

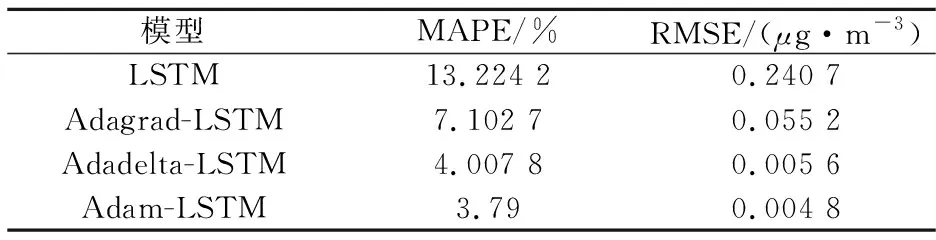
表2 预测误差指标

4 结论

本文在深度学习的LSTM神经网络预测空气质量运用基础上，提出了基于自适应调节学习率的随机梯度下降算法优化的LSTM神经网络模型，即：Adagrad-LSTM、AdaDelta-LSTM、Adam-LSTM.通过使用太原市的空气质量数据对四个模型进行模拟仿真，证明了本文使用的三种优化算法都能够有效地提高LSTM神经网络的预测精度和收敛速度，同时经过误差指标MAPE和RMSE的对比，可以看出Adam-LSTM模型的预测性能要比Adagrad-LSTM、AdaDelta-LSTM以及单一的深度学习模型要好，也充分表明了本文使用的模型在空气质量预测方面具有重要的价值意义.