带时间延迟工业最优控制问题扩展控制变量参数化算法

刘 航,仇国庆,刘 平,杨金凤,周 慧

(1.重庆邮电大学 自动化学院 工业物联网与网络化控制教育部重点实验室,重庆400065;2.重庆建筑工程职业学院 轨道与机电工程系,重庆400072;3.重庆机床(集团)有限责任公司,重庆401336)

1 前 言

带时间延迟最优控制问题(time-delay optimal control problem，TDOCP)的求解是实现时滞工业过程对象最优控制的一个核心[1-2]。在当前最优控制问题数值求解算法中，控制变量参数化(control variable parameterization，CVP)方法因具有求解精度高、离散化后非线性规划(nonlinear programming，NLP)问题规模较小等优点，在工业过程控制领域得到了众多学者的青睐[3-5]。近年来，国内外学者提出了诸多改进方法用于TDOCP 问题的求解。比如，Gui等[6]基于CVP 方法推导了带时间延迟系统的协态方法，并在锌冶炼过程TDOCP 问题中进行仿真试验，结果显示优化计算后锌粉原料可以有效减少；Yu 等[7]研究了混合时间尺度变换(hybrid time-scaling，HTS)HTS-CVP 方法进行时间延迟尺度转化，从而实现了TDOCP问题的有效求解；Lin 等[8]提出了2 种用于计算TDOCP 问题目标函数梯度信息的方法，实现了时滞非线性系统的参数预估。此外，Jajarmi 等[9]基于庞特里亚金极大值原理将TDOCP 问题转换为耦合两点边值问题，并推导了有限差分求解方法；文献[10]和文献[11]分别提出了单时间转化和终值时间转换算法用于终值时间不固定TDOCP 问题的求解。

对于传统CVP 方法，动态系统时间延迟的存在让状态变量和梯度信息的求解变得困难，进而影响到TDOCP 问题的高效求解，因此状态变量转化与梯度信息计算一直是研究的热点。然而，以传统CVP 方法为基础的目标函数和约束条件梯度求取方法[6-8]在算法复杂性和效率方面存在一定的不足，比如，协态方法通过构造Hamilton 函数得到协态系统进行梯度求取，但迟滞系统和协态系统因为初始值不同并不能同时求解，需要引入插值方法进行近似；时间尺度转化方法引入时间尺度变换可以实现时间节点的精确控制，但也增加了系统梯度信息求解的复杂度。因此，本文提出了一种求解TDOCP 问题的扩展控制向量参数化方法。首先，采用控制变量参数化技术和光滑化罚函数法将TDOCP 问题近似转化为不含路径约束的有限维NLP 问题；进一步，引入扩展变分系统通过辅助状态变量分析时间延迟状态变量扩展变分系统求解方法，以此实现迟滞系统与变分系统在统一初始时刻下求解；同时，针对扩展变分系统直接推导出目标函数和约束函数对于控制参数的梯度信息求解公式，为基于梯度信息的NLP 求解器提供高效梯度信息求取方法；最后，在两个典型工业过程TDOCP 问题上进行测试以验证所提方法的正确性和有效性。

2 问题描述

3 算法描述

3.1 控制变量参数化

3.2 时间延迟状态变量扩展变分系统

分析可知，由于时间延迟微分方程组的存在，问题(P2)中目标函数和约束函数对于控制参数σ的梯度

将式(10)入式(15)，即可得到定理4 式(14)，证毕。

3.3 算法步骤

结合3.1节和3.2节算法推导，给出时间延迟最优控制问题扩展控制变量参数化算法(extended control variable parameterization,Extended-CVP)实现过程，其算法流程如图1所示，主要步骤为：

步骤1.输入带时间延迟最优控制问题(P1)，设置控制时域分段数N，给定初始控制参数0σ；

步骤2.在分段数N下，采用PCF 函数对控制变量进行离散化，得到参数化后非线性优化问题(P2)；

步骤3.求解时间延迟状态变量扩展变分系统，得到辅助状态变量 ( )tΓ的值；

步骤4.采用式(14)得到g～l(σ) ,l∈ {0}∪E函数关于控制参数σ的扩展梯度信息；

步骤5.选择NLP 求解器求解问题(P2)，得到优化后最优控制参数σ*和目标函数g0(σ*)，输出优化结果。

图1 扩展控制变量参数化算法流程图Fig.1 Flow chart of extended control variable parameterization approach

4 仿真测试

图2 Soliman 和Ray 连续搅拌釜反应器生产过程Fig.2 Continuous stirred tank reactor of Soliman and Ray process

4.1 闭环连续搅拌釜反应器最优控制

表1 连续搅拌釜反应器最优控制问题结果对比Table 1 Result comparison of continuous stirred tank reactor optimal control problem

图3 连续搅拌釜反应器最优控制曲线Fig.3 Optimal control curvesof continuous stirred tank reactor

图4 连续搅拌釜反应器最优状态曲线Fig.4 Optimal state curves of continuous stirred tank reactor

4.2 状态延迟LQR 最优控制

本例以Jajarmi 等[20]研究的带状态延迟线性二次型调节器(linear quadratic regulator，LQR)为对象进行测试，其TDOCP 问题模型如下所示，模型中所采用的参数数值见表2。表中a、c为状态变量x(t)输入矩阵的取值参数，b为延迟状态变量x(t-h)输入矩阵的取值参数，h为时间延迟量，tf为最优控制终值时间，S为终值状态加权矩阵，Q为状态变量加权矩阵，R为控制变量加权矩阵。

测试中，控制时域采用等间隔方式划分，分段数设置为21、40和150，初始控制参数取σ0=1，NLP 求解器优化精度设置为10-4。对于上述LQR 最优控制问题，文献[20]以CVP 方法为基础推导了循环单射(recursive shooting，RS)RS-CVP 方法，通过8次循环迭代得到了18.110 3的当前文献最优目标函数值；文献[9]提出了改进的有限差分(finite difference，FD)方法，在21个优化参数下得到了18.450 2 的优化结果；文献[21]推导了迭代对偶谱方法(iterative symplectic pseudospectral method，ISPM)，在双重配点下计算得到的目标函数值为18.347 6。表3列出了文献方法和本文方法的求解结果，比较可知，在21个优化参数下，本文方法求得的优化结果为18.446 4，优于FD方法在相同优化参数下的结果，虽然本文方法的优化结果相比于RS-CVP 方法存在0.336 1的差距，但是本文方法只需要一次参数化迭代；同时，与文献[21]所求得结果进行对比发现，本文方法与ISPM方法的目标函数、系统状态曲线一致，显示出本文方法的实用性和正确性。图5、6分别给出了40分段数下Extended-CVP 方法求得的LQR 问题最优控制曲线和状态曲线，与文献结果一致，同时也很好地满足了控制要求，进一步表明了本文方法的效果。

表2 状态延迟LQR 问题参数值Table 2 Parametersof state time-delay LQR optimal control problem

表3 状态延迟LQR 问题结果对比Table 3 Result comparison of state time-delay LQR optimal control problem

图5 状态延迟LQR 问题最优控制曲线Fig.5 Optimal control curve of state time-delay LQR optimal control problem

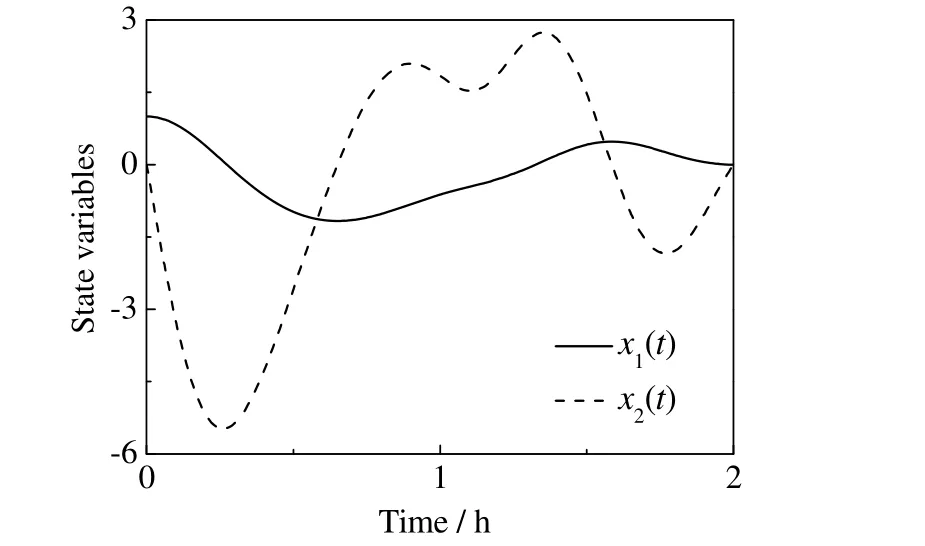
图6 状态延迟LQR 问题最优状态曲线Fig.6 Optimal state curvesof state time-delay LQR optimal control problem

5 结 论

本文提出了一种用于求解工业过程TDOCP 问题的扩展控制变量参数化算法。该方法通过引入辅助状态变量推导了时间延迟状态变量扩展变分系统，拓展了传统CVP 方法对于带时间延迟最优控制问题的求解能力；同时，给出了目标函数和约束函数对控制参数梯度信息的求解方法，为基于梯度信息的NLP求解器高效求解提供了支撑，保证了优化求解的精度和效率。所提出的方法针对连续搅拌釜反应器和LQR控制器两个典型TDOCP 问题进行了测试，结果显示提出方法能在较少优化参数下取得与文献结果相近甚至更优的结果，表明了本文方法的有效性和正确性。考虑非均匀时间间隔控制变量参数化和不确定参数进一步提升本文方法对TDOCP 问题的适用性是下一步工作计划开展的课题。