125I粒子源剂量计算参数模拟研究

刘川凤，宋明哲，王红玉，倪 宁，魏可新，刘蕴韬

(中国原子能科学研究院 计量测试部，北京 102413)

近距离治疗125I粒子源是一种低能量X射线放射源，剂量随距离增加而迅速减少，在治疗过程中对周围正常器官的损害较小，已成为永久性植入治疗放射源[1]，通常用于前列腺癌、肺癌和脑癌[2]的治疗。癌症治疗的关键在于对靶区剂量分布的精确掌握，靶区剂量分布与粒子源的几何结构有着很大的联系[3]。美国医学物理学家协会(AAPM)建议在临床实施前对粒子源剂量计算参数至少进行一套完整的实验测量和一套完整的蒙特卡罗计算[4]，采用蒙特卡罗模拟法，对粒子源的剂量计算参数初步研究，再利用实验方法进行验证。本文在曹振等[5]、孙亮等[6]研究基础上利用MCNP5程序对国产125I粒子源的源结构作更加细致的模型建立，得到TG43-U1[7]中的剂量计算参数，同时验证蒙特卡罗程序的正确性。

1 粒子源结构

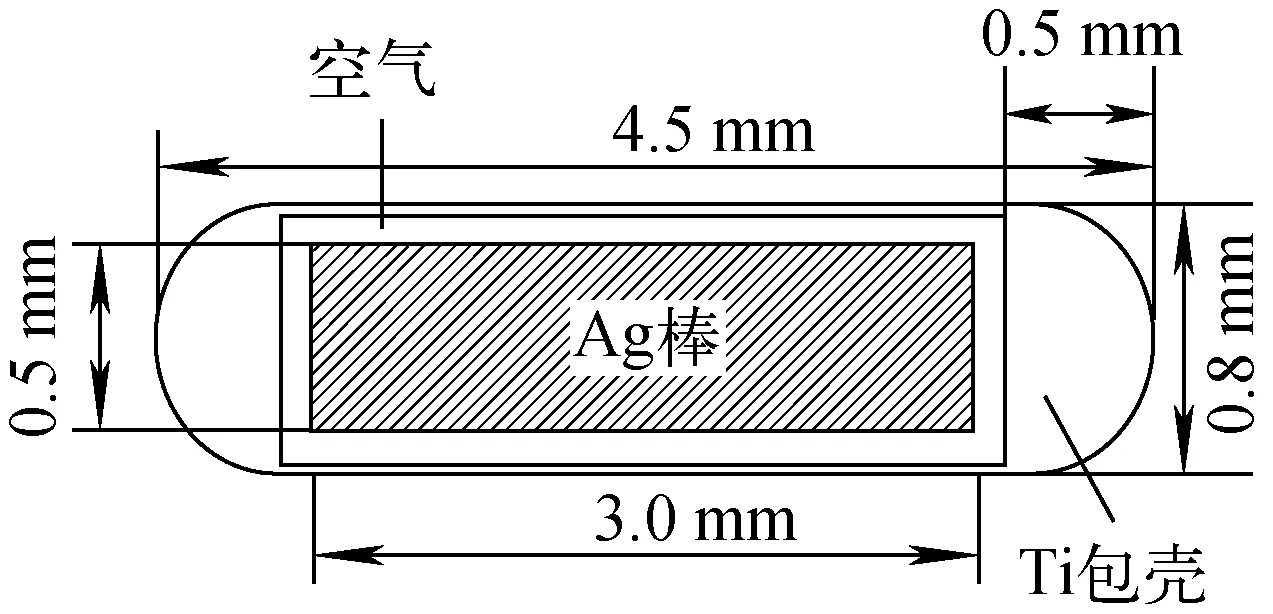
图1 125I粒子源结构示意图Fig.1Structure schematic of 125I brachytherapy source

125I粒子源结构如图1所示。外部包壳由Ti管构成，侧壁厚为0.05 mm，密度为4.54 g/cm3，两端通过激光焊接密封，近似认为厚度为0.5 mm的椭球形；Ti包壳内部是直径为0.5 mm、长为3.0 mm、密度为10.49 g/cm3的圆柱形银棒，银棒作为不透射X射线的成像标记点，用来鉴别粒子源类型；银棒表面均匀覆盖密度为6.245 g/cm3、厚度为1 μm的Br5125I2[8]，因此放射性活度区长度为3.0 mm。Ti包壳和银棒之间充满密度为0.001 205 g/cm3的空气，粒子源结构尺寸和材料组分由原子高科股份有限公司提供。125I粒子源发射能量[9]为：27.202 keV(0.259 5)、27.472 keV(0.498 1)、30.98 keV(0.155 6)、31.71 keV(0.034 7)和35.492 keV(0.052 1)，其中括号内为每次发射的光子数。

2 剂量计算参数和蒙特卡罗模拟

2.1 剂量计算参数

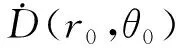
(1)

径向剂量函数g(r)计算公式为：

(2)

其中，GL(r,θ)为结构因子，与粒子源几何尺寸有关，计算公式为：

GL(r,θ)=(r2-L2/4)-1θ=0°

(3)

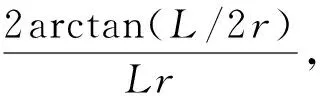
二维各向异性函数F(r,θ)计算公式为：

(4)

其中：r为测量点与粒子源中心的距离；β为测量点与粒子源活性区两端连线所成夹角；θ为测量点与中心点连线与粒子源长轴所成夹角，θ0=90°；L为粒子源活度区有效长度，本文L取值为3.0 mm。参考坐标系如图2所示。

2.2 蒙特卡罗模拟的理论模型和方法

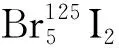
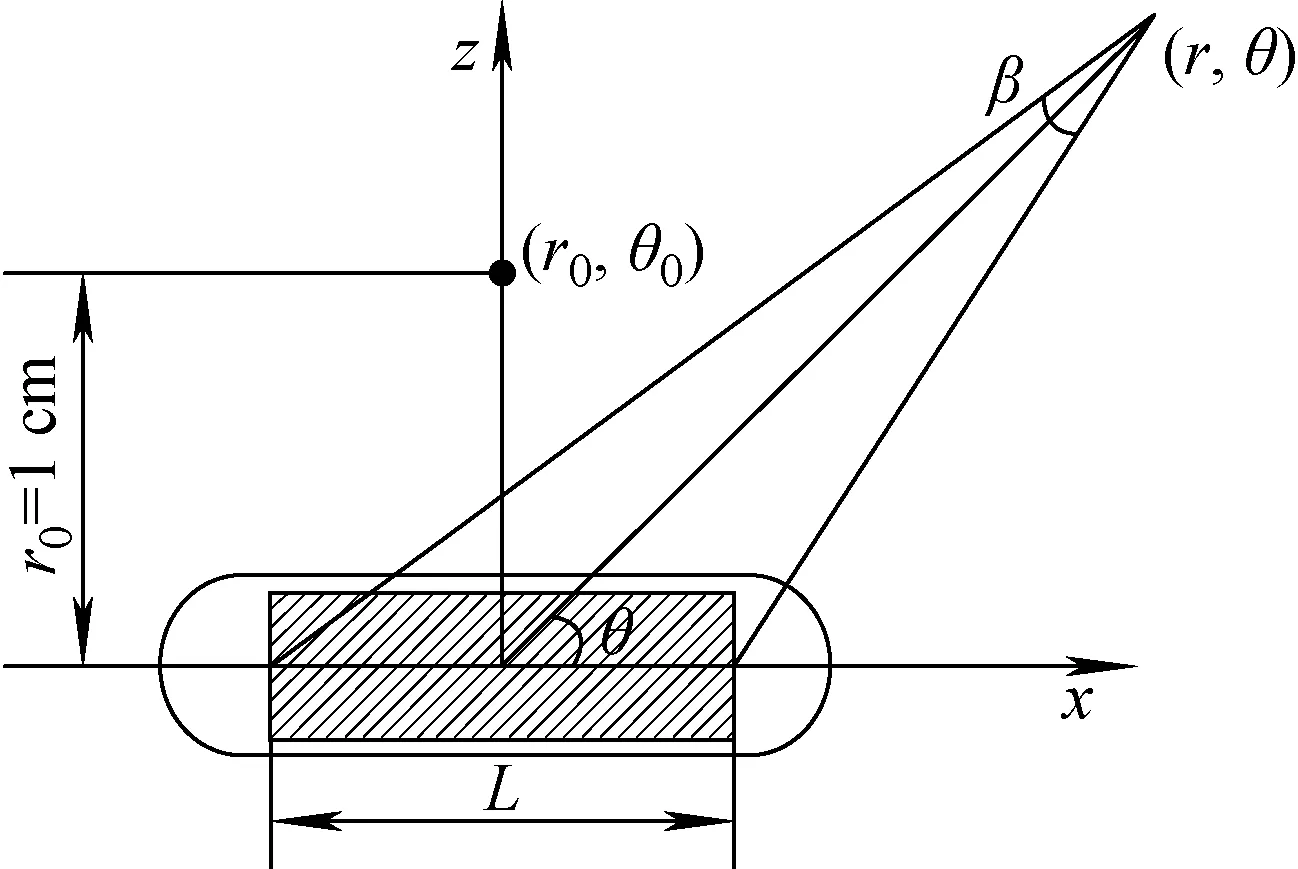
图2 剂量计算参数的参考坐标系Fig.2 Reference coordinate system of dose calculation parameter

计算水吸收剂量的方法为：将粒子源放置在充满液体水(ρ=0.998 g/cm3)、半径为15 cm的球模型中，可近似认为粒子源周围水组织内存在带电粒子平衡，碰撞比释动能等于水吸收剂量。利用点探测器F5计数卡，结合DE DF卡记录不同位置水吸收剂量，邻域半径设为0，为降低统计不确定度，粒子个数设为1.8×108，光子截止能量设为1 keV。由于本文放射性核发射的光子与介质相互作用产生的次级电子射程很短，因此不考虑电子输运，运行过程采用并行计算，运行1次约需300 min，模拟结果相对误差均小于0.05。

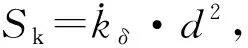
3 蒙特卡罗模拟结果

3.1 剂量率常数Λ

3.2 径向剂量函数g(r)

本文研究了近源处径向剂量函数g(r)的变化规律，模拟结果列于表1。当r<0.5 cm时，蒙特卡罗模拟结果相对误差小于0.6%；r>0.5 cm时，最大相对误差为2.72%。

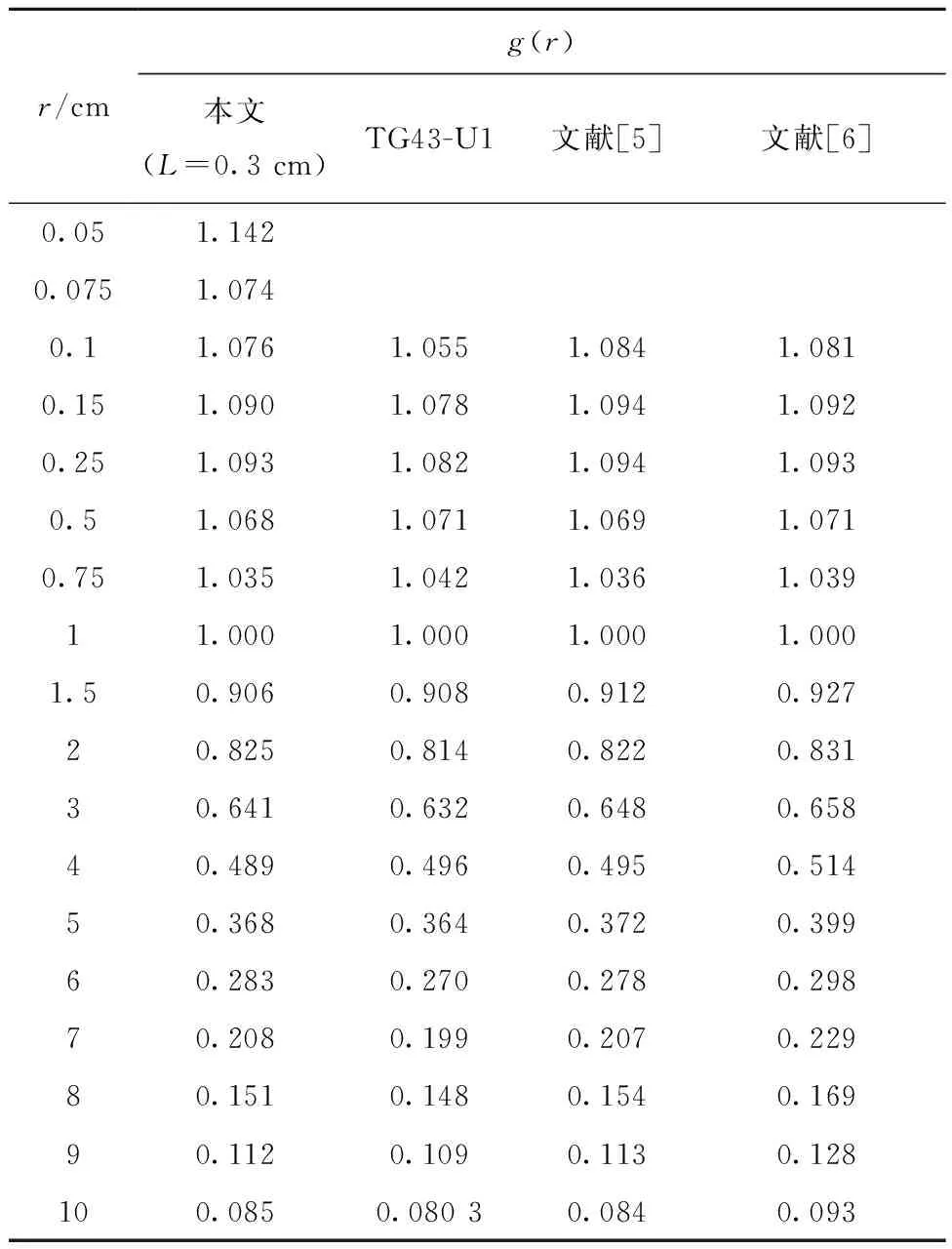
表1 径向剂量函数g(r)Table 1 Radial dose function g(r)

通过对比分析可看出：模拟结果的整体变化趋势与其他相关文献的变化趋势相同，结果也符合较好。与TG43-U1中的推荐值相比，比值变化范围为0.986～1.059；与文献[5]模拟结果相比，比值变化范围为0.990～1.020；与文献[6]模拟结果相比，比值变化范围为0.873～1.000，结果均很接近。

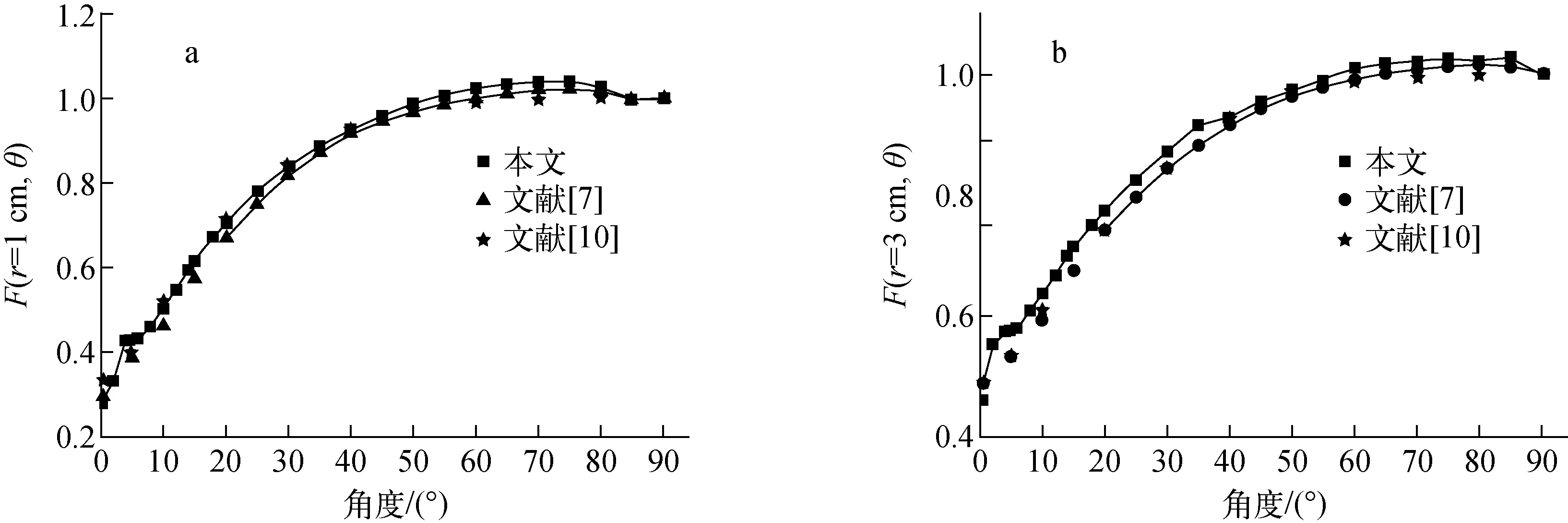
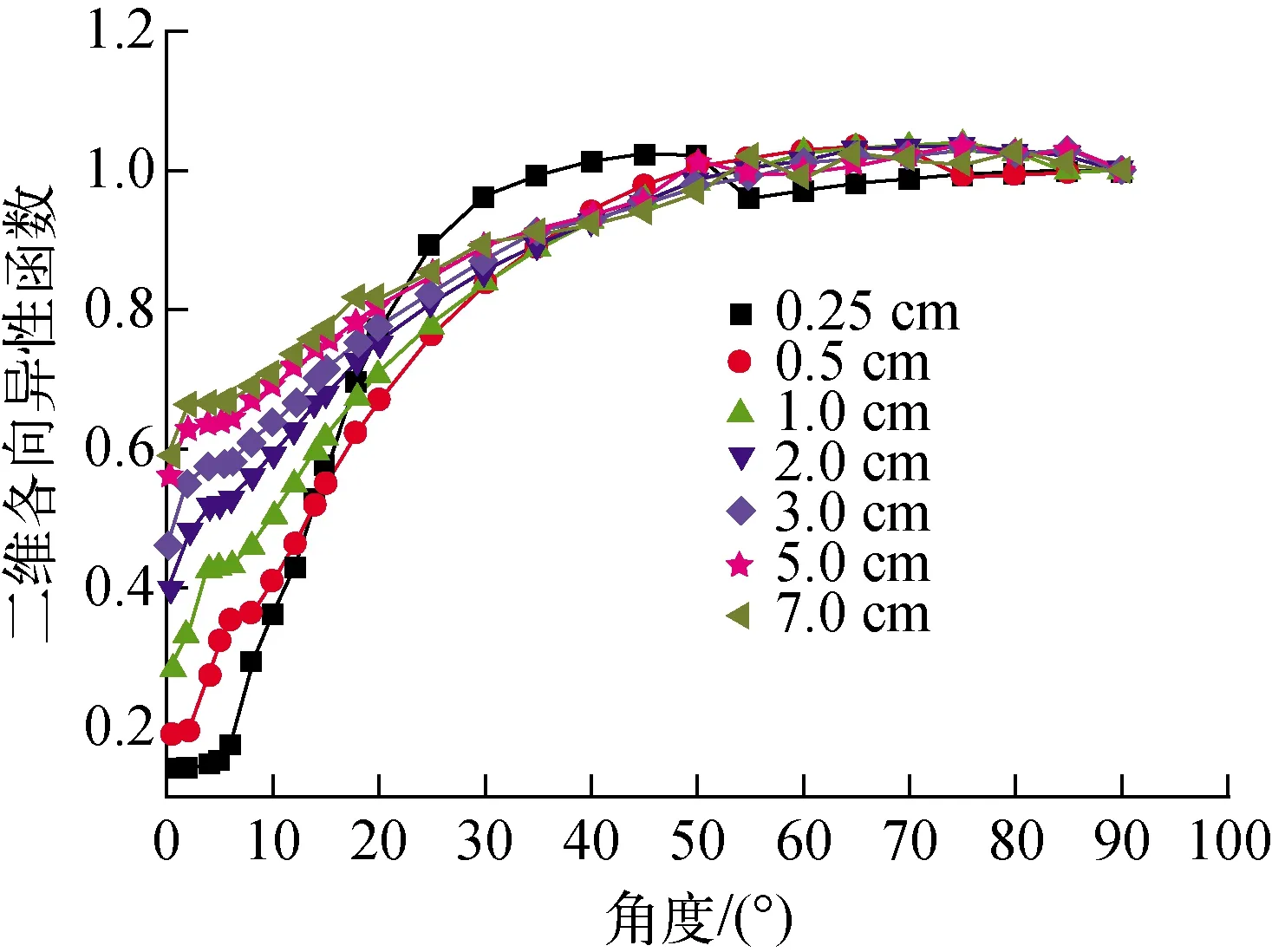
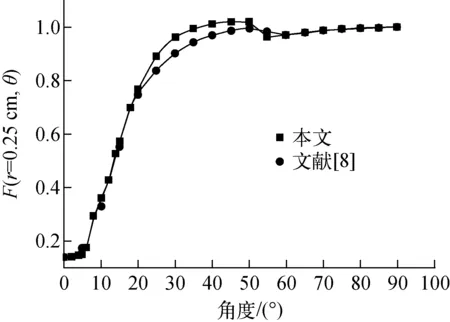
当0.05 cm

对0.1 cm

3.3 二维各向异性函数F(r,θ)

图3 二维各向异性函数Fig.3 2D anisotropy function

本文模拟了距离r为0.25、0.5、1.0、2.0、3.0、5.0和7.0 cm时的二维各向异性函数F(r,θ)，模拟结果如图3所示。可看出，曲线呈非单调性，当θ<45°时，不同的非单调行为是由于银标记边缘结构和钛包壳不同造成的。接近于源中心轴70°～85°的非单调行为主要是银标记末端发射光子受到屏蔽而引起的[12]。

为比较近源处(r=0.25 cm)二维各向异性函数的变化规律，与文献[8]的模拟结果进行比较，如图4所示。当θ<35°或θ>45°时，曲线变化趋势相同，而当θ处于35°～45°范围时二维各向异性函数产生驼峰，这一现象与文献[8]模拟的具有直角型末端银棒的Ag X100型125I粒子源的变化趋势相同。文献[8]中模拟的6711型银棒末端是45°斜切方向，造成这一现象的原因是由于当角度θ从35°到45°时，银棒的结构不同，源末端的银衰减变成空气和Ti包壳的衰减[16]。

图4 r=0.25 cm时二维各向异性函数对比Fig.4 Comparison of 2D anisotropy function with r=0.25 cm

为更好地观察银棒末端对二维各向异性函数的影响，对比了r=1 cm和3 cm时的二维各向异性函数，如图5所示，可看出，本文的模拟结果整体大于文献[7，10]的结果，这与文献[17]的结论一致，即银棒末端为直角型结构的粒子源的二维各向异性函数大于银棒末尾为斜切方向的二维各向异性函数，同时也说明本文模拟结果的可靠性。

4 结论

本文利用蒙特卡罗方法对银棒末端为直角型的国产125I粒子源的剂量计算参数进行模拟研究，采用复合源描述方法，建立更为精细的粒子源模型。模拟得到r为0.05～10 cm范围内的径向剂量函数，对r为0.1～10 cm范围内径向剂量函数进行五阶多项式拟合，此拟合公式可为治疗计划系统计算粒子源剂量分布提供参考。当r=0.25 cm时，直角型银棒结构会使二维各向异性函数在35°<θ<45°范围内产生1个驼峰，这与银棒末端为斜切方向时的结果不同，因此在计算粒子源剂量分布时需额外注意这一点。模拟结果表明银棒末端为直角型结构时125I粒子源的二维各向异性函数比银棒末端为斜切方向的二维各向异性函数大。

a——r=1 cm；b——r=3 cm 图5 r=1、3 cm时二维各向异性函数对比Fig.5 Comparison of 2D anisotropy function with r=1 cm and r=3 cm

蒙特卡罗模拟计算方法无法对粒子源内部动态流动性进行模拟，但在一定合理范围内近似建立粒子源内部结构和放射性核素的分布，得出的模拟结果对实践应用具有一定的指导性。