棒状氢化锆慢化钍基熔盐堆燃料组件稳态核热耦合程序开发

朱 帆，伍建辉，余呈刚，马玉雯,*，陈金根,*，蔡翔舟

(1.中国科学院 上海应用物理研究所，上海 201800；2.中国科学院 先进核能创新研究院，上海 201800；3.中国科学院大学，北京 100049)

考虑到材料的工作温度、慢化吸收比、化学稳定性和价格等因素，熔盐堆一般采用石墨作为慢化剂，堆芯由六边形或四边形通道式石墨组件排布而成，但石墨的慢化能力较弱且辐照后需定期更换[1-4]。氢化锆作为另一种较好的慢化剂材料，其慢化能力优于石墨且具有较好的热稳定性和耐高温抗辐照等特点，不过因其物理和材料特性，氢化锆一般被制成棒状插入熔盐中[5-7]。因此，棒状氢化锆慢化钍基熔盐堆(ZrH-MSR)在中子学和热工水力学方面与传统压水反应堆和石墨慢化熔盐堆均有较大不同。与传统压水反应堆相比，熔盐既是裂变热源也是冷却剂，需依靠燃料盐流动带走热量。而与石墨慢化熔盐堆相比，ZrH-MSR为开式通道，相邻通道间熔盐存在横向的质量、动量和能量交换(横向交混)，各熔盐通道内质量流密度沿轴向可能不断发生变化，使通道内熔盐温度也产生相对应的变化。

ZrH-MSR作为一种新型熔盐堆，在核热耦合模拟方面尚缺少适用的分析工具。本文基于蒙特卡罗粒子输运程序MCNP与自主开发的子通道热工水力程序SubTH，进行核热耦合程序MCNP-SubTH的开发，可为ZrH-MSR堆芯设计提供分析和优化手段。

1 MCNP-SubTH耦合程序计算方法

MCNP-SubTH的中子学程序由MCNP5计算程序、NJOY99截面加工程序和ENDF/B-Ⅶ核数据库构成，利用NJOY99生成不同温度点下的截面数据并采用伪材料法插值，可得到较高的MCNP计算精度。为实现高精度的核热耦合计算，需针对ZrH-MSR流动传热特性开发适用的热工水力学程序。本文基于子通道模型开发了热工水力学程序SubTH，该程序不仅充分考虑了ZrH-MSR相邻通道间熔盐存在的横向交混问题，也考虑了燃料盐既是内热源也是冷却剂的特点。

MCNP-SubTH采用交错网格的映射方式实现物理-热工网格匹配，物理模型与热工模型中慢化棒与慢化棒相互对应，物理模型中熔盐网格是由热工模型中每个慢化棒周围的4个熔盐通道所组成，解决了稳态核热耦合程序因网格类型不同难以耦合的问题，可为ZrH-MSR提供更准确的堆芯核热耦合计算。

1.1 中子学模型

MCNP是一款基于蒙特卡罗方法的粒子输运计算程序，已广泛运用于反应堆临界计算、辐射屏蔽设计等领域，其计算精度得到了国际认可[8]。因此采用MCNP对ZrH-MSR复杂的堆芯结构建模是一合理选择，它能为热工程序提供准确的三维内热源分布。

此外，由于ZrH-MSR堆芯同时存在热反馈和反应性反馈，其熔盐温度和密度、慢化剂温度、中子截面等会产生相互耦合变化。材料密度变化会影响各栅元材料的密度设定，而温度变化则影响计算所需的中子截面数据，从而迭代计算时需更新对应的密度和截面数据供MCNP使用。目前，针对中子截面数据更新提出了3种方法：NJOY在线加工法、多普勒展宽法和伪材料法[8]。与伪材料法相比，NJOY在线加工法需在每次迭代过程中对所有温度点运行NJOY计算所对应的中子截面，这种方法计算结果最为精确但所需计算时间也最多。多普勒展宽法涉及中子截面数据的高精度拟合，其拟合参数取决于中子能量和材料温度，但该方法尚未应用于MNCP5中。因此，综合考虑中子截面数据精度与程序计算效率，本文选择伪材料法，用于与温度相关截面数据的更新。

伪材料法认为，由于共振能量附近温度所对应的截面近似服从平方根规律，则核素在某一温度下的截面可用相邻的较低温度和较高温度所对应截面的加权平均值近似：

Σ(T)=wlowΣ(Tlow)+whighΣ(Thigh)

wlow=1-whigh

(1)

式中：T为目标温度；Σ(T)为核素在温度T下所对应的宏观截面；Tlow和Thigh分别为温度T所在区间的较低和较高温度，其对应的宏观截面分别为Σ(Tlow)和Σ(Thigh)；wlow和whigh分别为温度Tlow和Thigh处的权重系数。

1.2 热工水力学模型

针对ZrH-MSR堆芯中燃料盐既是内热源也是冷却剂，且相邻通道间熔盐存在横向交混的特点，本文基于子通道模型[9]编写了热工水力分析程序SubTH，其计算流程如图1所示。首先，读入堆芯功率分布、子通道几何参数等文件，并假设各子通道内初始轴向压降损失相同，计算轴向动量守恒方程得到燃料盐轴向流动速度，同时修正各子通道内轴向压降，直至总质量流量收敛。其次，进行燃料盐质量守恒方程和横向动量守恒方程计算，得出各子通道内燃料盐的横向流速和压降。然后，进行能量守恒方程计算，得出每个网格内的温度分布。最后，完成所有轴向网格计算并判断燃料盐温度收敛后，输出燃料盐轴向速度、密度和温度分布等参数。

燃料盐质量守恒方程为：

(2)

式中：ρi为子通道i内燃料盐的密度；z为轴向高度；ui为子通道i内燃料盐的流速；Ai为子通道i的流通面积；ρ′为子通道i与j内燃料盐的平均密度；vij为子通道i的燃料盐向相邻子通道j的横流速度；Sij为子通道i与j间的连接长度。式(2)左边第1项为子通道i内轴向质量流量的变化，第2项为子通道i内流出和流进的横向流量的变化。

图1 SubTH计算流程Fig.1 Calculation flow chart of SubTH

燃料盐能量守恒方程为：

(3)

式中：hi、hj分别为子通道i与j内燃料盐的焓值；Ti、Tj分别为子通道i与j内燃料盐的温度；h′为子通道i与j内燃料盐的平均焓值；qfuel-salt为燃料盐线功率；k为导热系数；lij为子通道i与j间的质心距；wij为湍流交混量，wij=β·G·Sij，其中湍流交混系数β=a·Reb，系数a、b均由经验关系式给出[10-11]。式(3)左边第1项为子通道i内轴向能量的变化，左边第2项为子通道i内横向能量的变化；右边第1项为燃料盐的裂变功率，第2～4项分别为轴向热传导带走的热量、熔盐由于横向温差引起的横流带走的热量、相邻通道间熔盐湍流交混带走的热量。

燃料盐轴向动量守恒方程为：

(4)

式中：u′为子通道i与j内燃料盐的平均流速；pi为子通道i的轴向压力；f为摩擦阻力系数；Dh为当量水力直径；K为形阻系数；Δz为子通道i的轴向高度；g为重力加速度；θ为子通道i的轴线与水平面间的夹角；CT为燃料盐横向交混因子；w′为有效湍流交混量。式(4)左边第1、2项之和为子通道i内轴向压降的变化；右边第1项为子通道i的轴向压力变化，第2～5项分别为子通道i的摩擦压降、形阻压降、提升压降及子通道i与子通道j内耦合引起的流阻压降。

燃料盐横向动量守恒方程为：

(5)

式中：vk为子通道i的燃料盐向相邻的第k个子通道的横流速度；βk为子通道i与k之间的夹角；pj为子通道j的轴向压力；kg为横向阻力系数。式(5)左边第1、2项之和为子通道i内横向压降的变化，右边第1项为相邻通道间的横向压力变化，右边第2项为通道间耦合引起的横向摩擦压降。

1.3 耦合方案

MCNP-SubTH采用外耦合的方式，实现MCNP与SubTH之间功率、密度和温度等数据的交换，其计算流程如图2所示。

MCNP-SubTH的计算步骤如下：1) 利用NJOY程序借助ENDF/B-Ⅶ数据库产生不同温度点的截面数据库；2) 耦合计算前划分MCNP输入卡中熔盐和慢化剂区域与SubTH程序中控制体相对应，并将每个熔盐和慢化棒的控制体进行编号，其网格映射关系如图3所示，迭代过程中可根据中子或热工程序的模拟需求，提供各网格节点对应的数据(包括功率、密度和温度等)；3) 给定一初始温度和密度的MCNP输入文件，调用MCNP进行计算，将F7卡统计的堆芯裂变沉积能量分布存入指定文件；4) 根据物理-热工网格对应关系，将存入的裂变沉积能量分布数据进行处理，并传递给子通道程序输入文件以更新输入参数，随后调用SubTH程序执行计算，计算结束后将各节点的温度及密度等参数分别存储；5) 根据网格间的映射关系，将SubTH计算得到的热工数据进行处理，以更新MCNP输入卡；6) 将熔盐温度是否收敛作为耦合程序结束判定标准，如式(6)所示。

max(ern)≤0.001n∈(1,N)

(6)

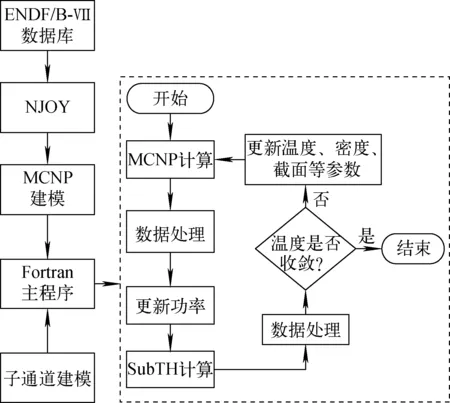
图2 MCNP-SubTH耦合程序计算流程Fig.2 Calculation flow chart of MCNP-SubTH coupling code

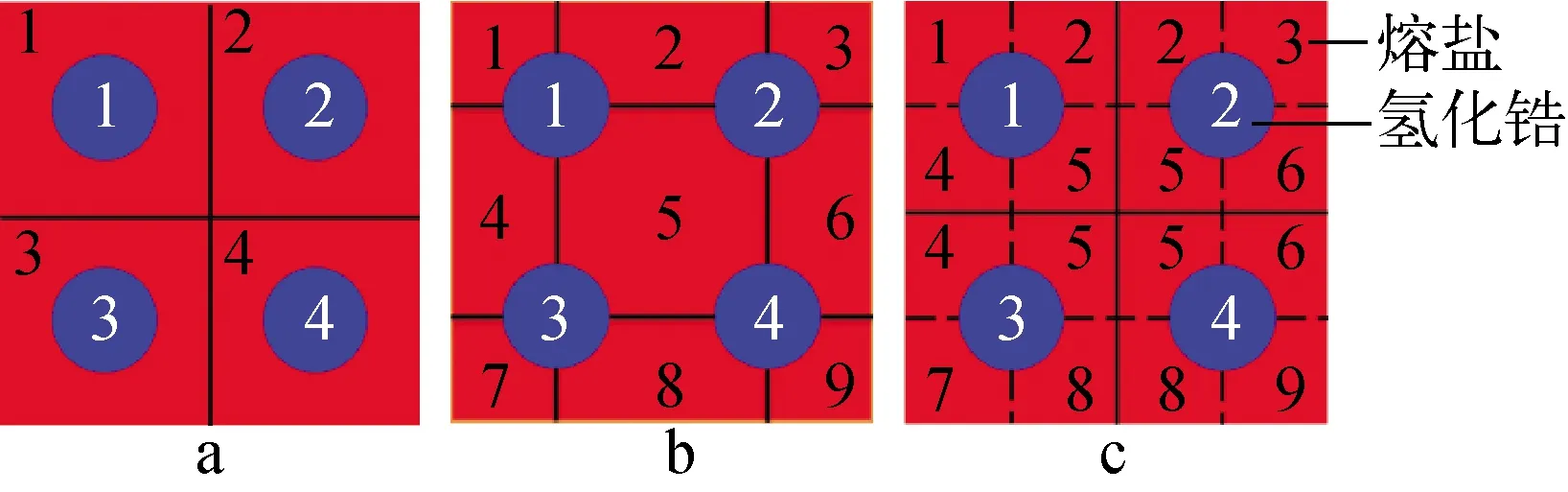
a——物理模型；b——热工模型；c——耦合模型图3 MCNP-SubTH网格映射关系Fig.3 Mesh mapping relationship in MCNP-SubTH

2 MCNP-SubTH耦合程序验证

目前还没有可用的ZrH-MSR耦合基准题或是已经验证过的ZrH-MSR稳态核热耦合程序，因此采用分模块验证方式，分别对MCNP-SubTH耦合程序的物理模块、热工模块和数据交换模块的准确性进行校验。

2.1 物理模块

MCNP计算偏差主要来源为伪材料法产生的截面数据的精确度。因此，本文选取了ZrH-MSR六边形单栅元模型(慢化棒直径为2.63 cm，栅元边长为2.31 cm，燃料盐为77.5 mol%LiF-22.5 mol%(HM)F4)来进行伪材料法的精确性验证，分别对比了采用NJOY在线加工法和伪材料法在800、900、1 000和1 100 K温度下的计算结果。表1列出有效增殖因数、裂变反应率和俘获反应率计算结果的对比。表1中，CASE A为采用NJOY直接加工得到某一温度点的截面数据(基准值)，CASE B为采用伪材料法以50 K为间隔进行插值得到某一温度点的截面数据。结果表明，两种方法得到的计算结果符合较好。

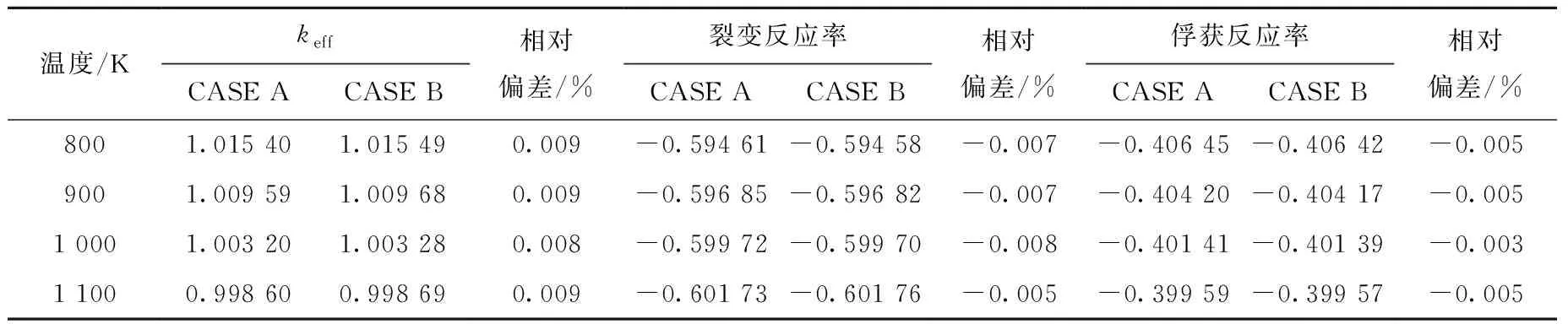
表1 有效增殖因数、裂变反应率和俘获反应率计算结果的对比Table 1 Comparison of calculation result of keff, fission reaction rate and capture reaction rate

此外，为验证伪材料法对于功率分布的影响，本文分别对比了采用NJOY在线加工法和伪材料法在800、900、1 000和1 100 K温度下各网格内的功率(轴向划分200个控制体，每个控制体轴向高度为0.5 cm)。结果表明，在不同温度下，伪材料法与NJOY在线加工法计算得到的各网格功率数据吻合较好，最大相对偏差为0.01%，证明了伪材料法可适用于ZrH-MSR核热耦合计算。

2.2 热工模块

热工模块采用Fluent计算结果作为验证基准。选取了3种典型的堆芯子通道划分方案(4棒束矩形通道、7棒束六边形通道和7棒束圆形通道)进行SubTH程序准确性验证。使用Gambit软件建模，并进行网格划分。将Gambit划分完成的网格文件导入Fluent中，设定进、出口等边界条件，加载熔盐(77.5 mol%LiF-22.5 mol%(HM)F4)、慢化剂(ZrH1.6)等物性参数，最后进行模拟计算。由于ZrH-MSR中熔盐的雷诺数较高，Fluent计算中采用标准k-ε湍流模型，使用Simple算法，收敛残差设为10-6。

矩形通道的子通道划分方案如图4a所示，横向划分了9个子通道，轴向划分了60个控制体。其中，矩形通道边长为8 cm，高为150 cm，慢化棒直径为2.63 cm，入口流速为0.5 m/s，入口质量流量为8.7 kg/s，入口温度为923.15 K，功率均匀分布，功率密度为120 MW/m3。网格划分方案如图4b所示，整个模型网格数量达到72万。

图4 矩形通道的子通道(a)和网格(b)划分方案Fig.4 Division scheme of sub-channel (a) and mesh (b) for rectangle channel

图5示出Fluent计算的矩形通道温度及熔盐轴向温度分布。从图5b可见，SubTH与Fluent计算结果吻合较好，最大相对偏差为0.45%。

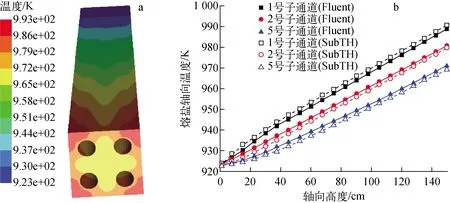
图5 矩形通道温度(a)及熔盐轴向温度(b)分布Fig.5 Distribution of rectangle channel temperature (a) and axial temperature of molten salt (b)

2) 7棒束六边形通道

六边形通道的子通道划分方案如图6a所示，横向划分18个子通道，轴向划分60个控制体。其中，六边形通道边长为6 cm，高为150 cm，慢化棒直径为2.63 cm，入口流速为0.5 m/s，入口质量流量为11.4 kg/s，堆芯入口温度为923.15 K，功率均匀分布，功率密度为120 MW/m3。网格划分方案如图6b所示，整个模型网格数量达到216万。

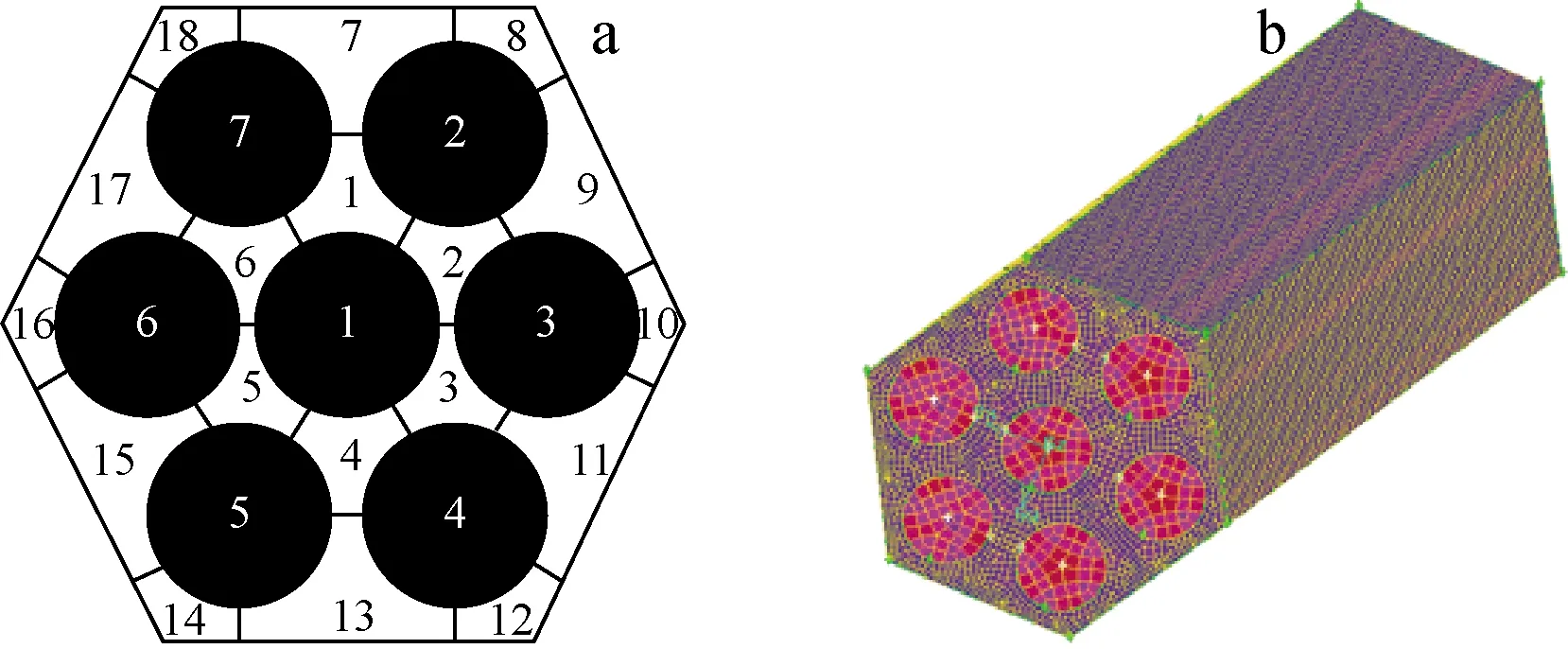
图6 六边形通道的子通道(a)和网格(b)划分方案Fig.6 Division scheme of sub-channel (a) and mesh (b) for hexagon channel

图7示出Fluent计算的六边形通道温度及熔盐轴向温度分布。由图7b可见，1号子通道的温度最低，8号子通道的温度最高，SubTH与Fluent计算结果吻合较好，最大相对偏差为0.40%。

3) 7棒束圆形通道

圆形通道的子通道划分方案如图8a所示，横向划分12个子通道，轴向划分60个控制体。其中，圆形通道直径为12 cm、高为150 cm，慢化棒直径为2.63 cm，入口流速为0.5 m/s，入口质量流量为15.4 kg/s，堆芯入口温度为923.15 K，功率均匀分布，功率密度为120 MW/m3。网格划分方案如图8b所示，整个模型网格数量达到223万。

(3)课后巩固。课后巩固环节很重要。在这一环节要求学生进行知识点的自我总结，完成相应的测试，进行自我检查。开展师生交流，学生可以通过发帖提出自己的疑惑，学生之间的交流不但解决了问题，还开拓了视野。通过这些环节的实施，将课程的学习融入整个过程中，强化了过程学习，培养学生终生学习的品质。

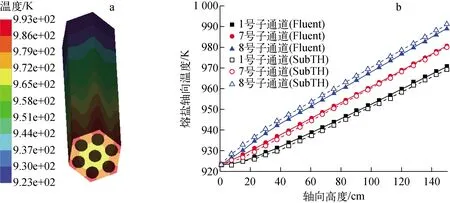
图7 六边形通道温度(a)及熔盐轴向温度(b)分布Fig.7 Distribution of hexagon channel temperature (a) and axial temperature of molten salt (b)

图8 圆形通道子通道(a)及网格(b)划分方案Fig.8 Division scheme of sub-channel (a) and mesh (b) for circle channel

图9示出Fluent计算的圆形通道熔盐温度及熔盐轴向温度分布。圆形通道的子通道只有内、外两层，对应的熔盐轴向温度曲线也为两条。从图9b可见，SubTH与Fluent计算结果吻合较好，最大相对偏差为0.42%。

基于Fluent对SubTH计算的不同棒束结构模型结果进行了验证，熔盐温度相对偏差小于0.45%，证明了SubTH在ZrH-MSR热工水力分析中的正确性和可靠性。

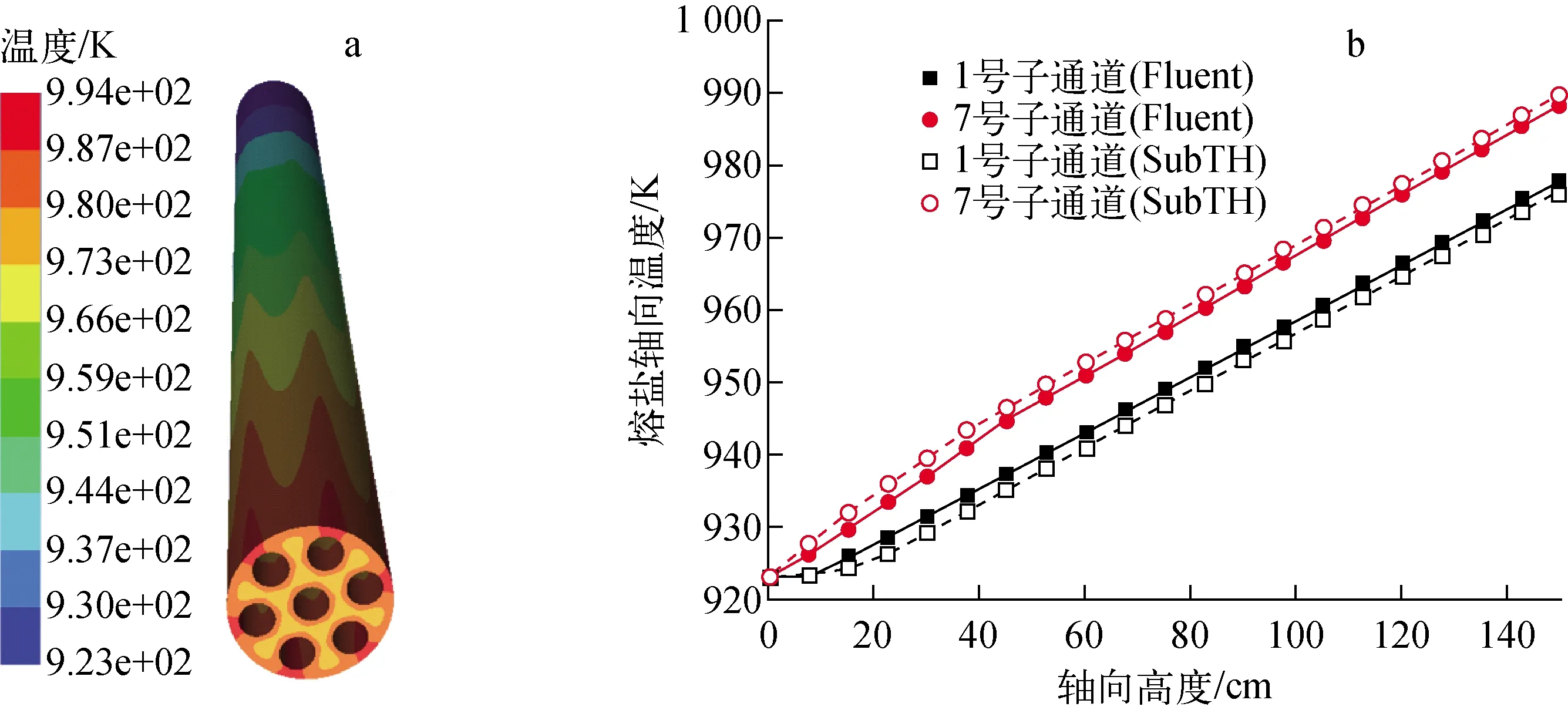
图9 圆形通道温度(a)及熔盐轴向温度(b)分布Fig.9 Distribution of circle channel temperature (a) and axial temperature of molten salt (b)

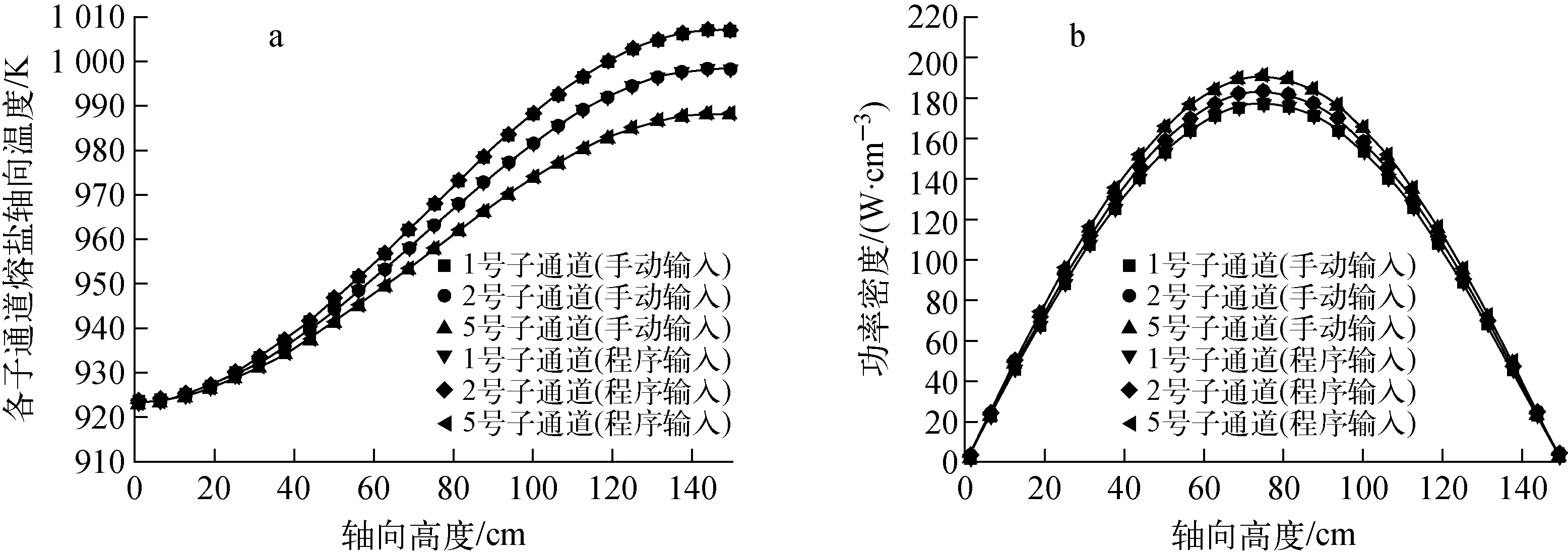
图10 不同子通道熔盐轴向温度和功率的分布Fig.10 Distribution of axial temperature and power of molten salt in different sub-channels

2.3 数据交换模块

由于耦合程序采用外耦合方式，因此需验证迭代计算时物理与热工模块间数据处理及传递的正确性，从而确保耦合程序的可靠性。本文分别采用手动输入和程序输入两种方式对上述3种典型的堆芯子通道模型进行计算。计算流程如下：首先将MCNP计算得到的功率分布手动输入到SubTH中，计算燃料盐温度和密度场分布；其次将计算得到的燃料盐温度和密度场分布再手动输入到MCNP中，重新计算功率分布；最后将采用手动输入方式迭代计算后的熔盐温度和功率分布与直接使用耦合程序的计算结果进行对比，来验证耦合程序的可靠性。以4棒束矩形通道为例(热功率为1 MW，功率余弦分布)，图10示出不同子通道熔盐温度和功率的分布。结果表明，两者的计算结果符合较好，证明了耦合程序的准确性和可靠性。

3 ZrH-MSR堆芯燃料组件稳态核热耦合分析

基于优化完成的ZrH-MSR堆芯模型[12]，选取六边形燃料组件作为算例，其子通道划分方案如图11所示，横向划分78个子通道。此外，考虑到熔盐堆在线添料会造成熔盐轴向分布不均匀效应，将轴向划分640个控制体，近似认为熔盐成分在每个细网格内不变。该组件边长为12.68 cm，高为320 cm，由37根直径为2.63 cm ZrH1.6慢化棒组成，棒与棒之间区域为77.5 mol%LiF-22.5 mol%(HM)F4的燃料盐，入口流速为1.5 m/s，入口质量流量为141.0 kg/s，入口温度为923.15 K，热功率为20 MW。此外，基于ORNL针对TAP反应堆的研究结果，本文假定ZrH慢化棒中存在1.25%的裂变沉积能量[13]。

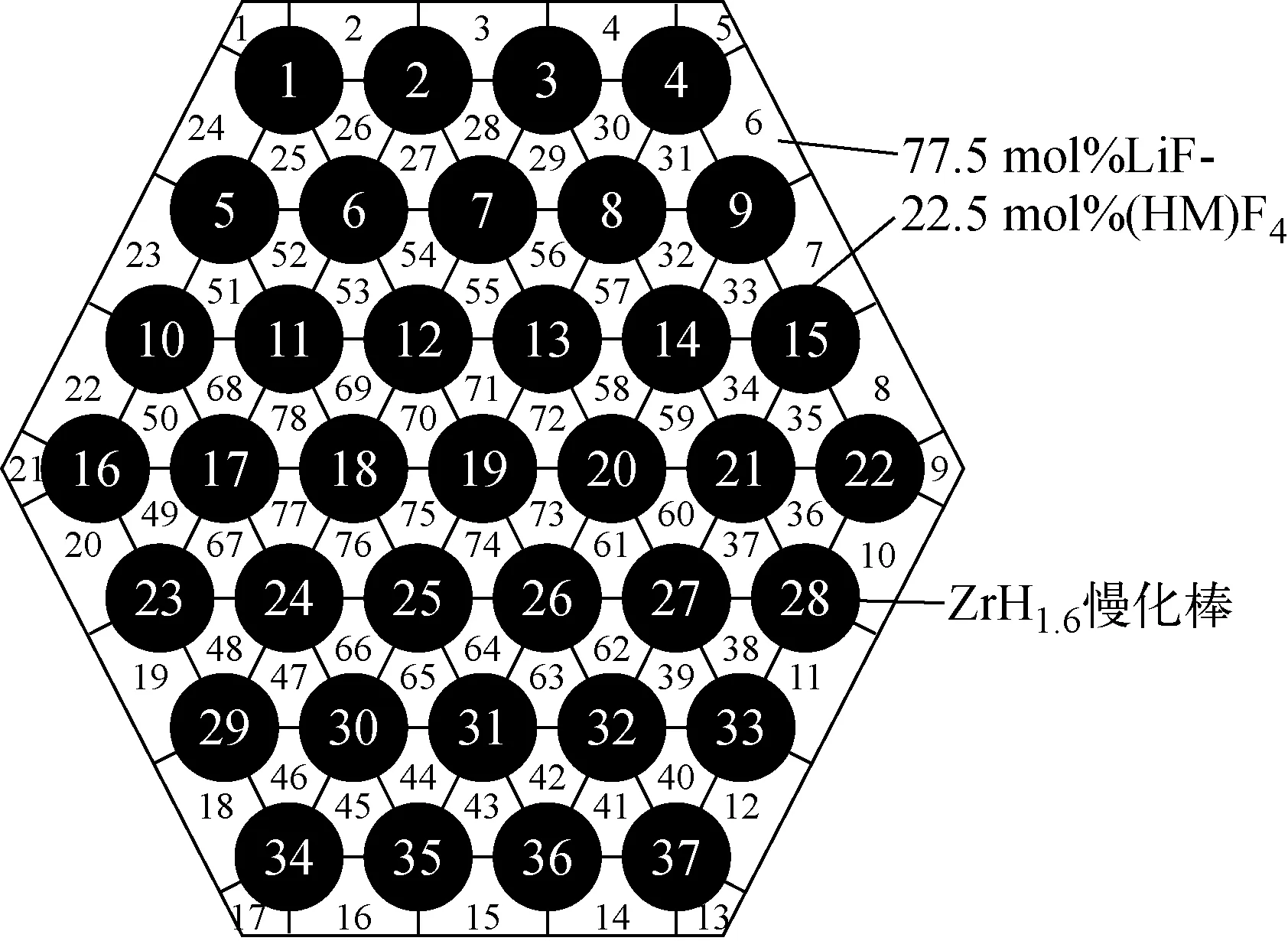
图11 ZrH-MSR燃料组件子通道划分方案Fig.11 Sub-channel division scheme of ZrH-MSR fuel assembly

3.1 初始温度无关性验证

采用800、923.15和1 100 K的初始温度对MCNP-SubTH的初始无关性进行了验证，如图12所示。由图12可见，虽然初始设定温度值不同导致计算得到的初始keff差别较大，但是经过1次耦合迭代后，它们的keff基本达到重合，且随迭代次数的增加，keff趋近于同一值。因此，耦合程序具有初始无关性。

3.2 温度分布

图13示出稳态情况下不同子通道熔盐轴向温度分布。由图13可见，随轴向高度的增加，各子通道内熔盐温度均不断增大，但在进出口附近熔盐温度增加缓慢。这是由于随轴向高度的增加，轴向功率不断增大，从而熔盐温度也逐渐增加，但因组件轴向功率呈余弦分布，导致进出口处附近功率增加缓慢，从而进出口处熔盐温度变化缓慢。

图12 keff随耦合迭代次数的变化Fig.12 Change of keff with iteration

图13 不同子通道熔盐轴向温度分布Fig.13 Axial temperature distribution of molten salt in different sub-channels

此外，在相同轴向高度下不同子通道间熔盐温度差距较大。这主要是由于组件内功率分布不均匀效应造成的，以1号子通道和71号子通道为例，尽管1号子通道的流通面积和湿润周长等参数较小应不利于传热，但71号子通道位于组件中心区域功率较高，而1号子通道位于组件角落功率较低(图14)，与流通面积和湿润周长等热工参数相比，此时功率分布不均匀效应占主导地位，从而导致越靠近组件中心区域的熔盐温度越高。同时，计算可得该六边形燃料组件径向、轴向功率峰因子分别为1.43和1.25，总功率峰因子为1.79，高于传统的压水反应堆总功率峰因子(约1.40)。当进行ZrH-MSR堆芯详细设计时，需进一步优化组件大小、慢化棒数目及布置位置等展平堆芯功率分布，以减小各通道出口温差。

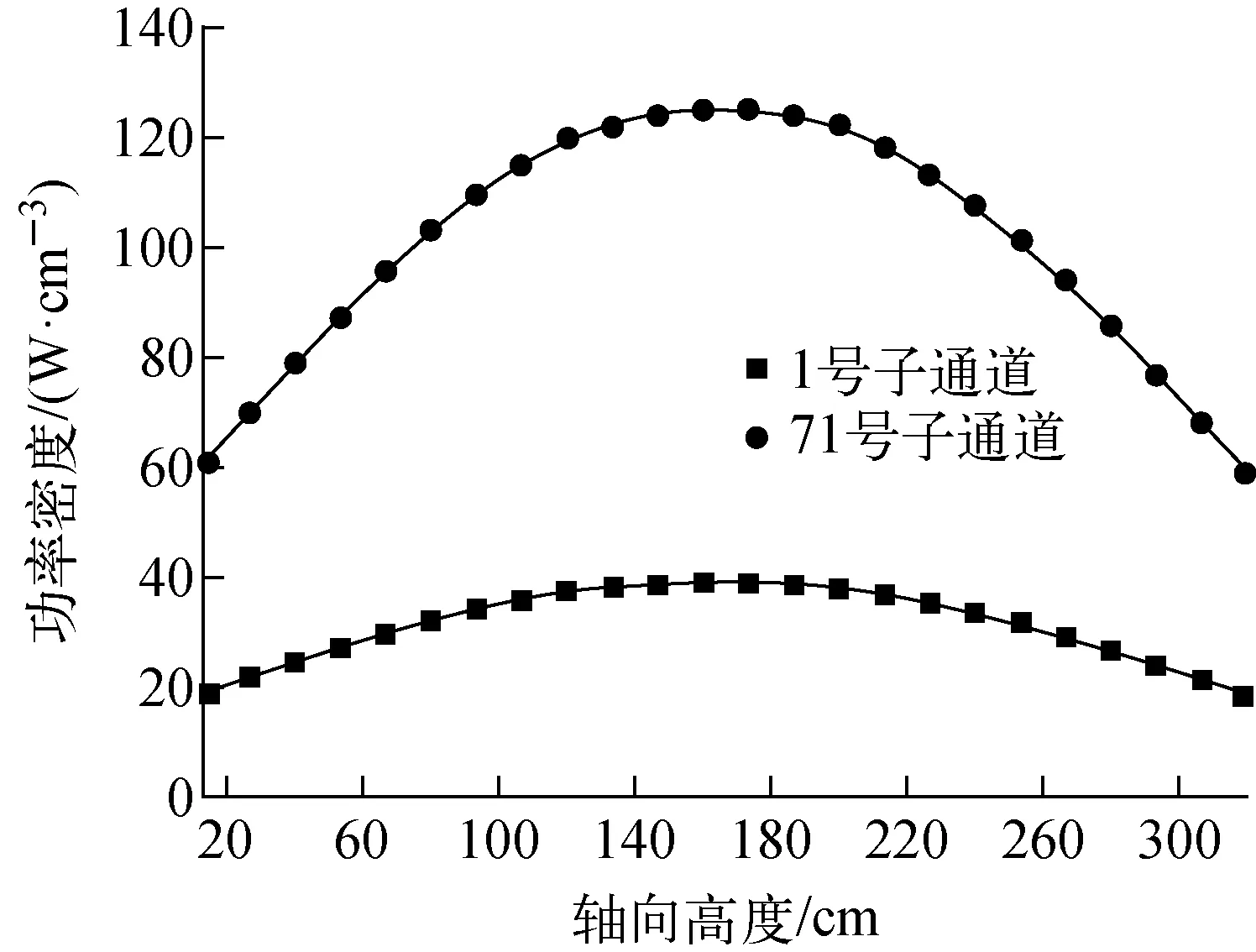
图14 不同子通道熔盐轴向功率分布Fig.14 Axial power distribution of molten salt in different sub-channels

图15示出稳态情况下最热熔盐通道(71号子通道)、ZrH慢化棒外表面(19号慢化棒)轴向温度分布和ZrH慢化棒径向温度分布(19号慢化棒，轴向高度为236 cm)。由图15可见，ZrH慢化棒轴向温度比熔盐温度高，这是由于一定比例的裂变能量沉积在ZrH慢化棒内，造成ZrH慢化棒温度会高于熔盐温度，通道内流动的熔盐对ZrH慢化棒起到冷却作用。此外，ZrH慢化棒轴向、径向最高温度分别为1 077.98 K和1 078.51 K，均低于ZrH最高破坏温度1 200 K[5]。

图15 熔盐、ZrH慢化棒轴向温度分布和ZrH慢化棒径向温度分布Fig.15 Axial temperature distribution of molten salt and radial temperature distribution of ZrH moderator

4 结论

本文针对ZrH-MSR中熔盐既是裂变热源也是冷却剂，和相邻通道间熔盐存在横向交混的问题，基于子通道方法的热工程序SubTH，耦合粒子输运程序MCNP开发了一套用于ZrH-MSR稳态核热耦合分析程序MCNP-SubTH，并与Fluent计算结果进行对比，验证了耦合程序的准确性。使用该程序对六边形ZrH-MSR燃料组件进行模拟，计算其功率分布、熔盐和ZrH慢化棒温度分布等数据，验证了MCNP-SubTH耦合程序的可行性及有效性。关于材料的相容性问题，需进一步实验研究。