基于桥梁健康监测的支座纵向位移时滞效应的研究
李 宁,朱晨辉
(1.山东高速股份有限公司,山东 济南 250014;2.山东高速工程检测有限公司,山东 济南 250002;3.桥梁结构大数据与性能诊治提升交通运输行业重点实验室,山东 济南 250002)
引言
健康监测系统是一种利用智能传感器在线监测结构“健康”状态的技术,借助埋入或表面粘贴的传感器感知结构整体和局部的变形、刚度、应力应变、阻尼、振动频率和环境荷载变化,推断结构内部的缺陷和损伤,是一种对结构进行实时无损评估的系统。由于结构是一个整体的系统,数据间存在诸多关联,根据数据的关联性对数据进行处理,可为数据异常诊断提供判定依据。
温度效应是影响桥梁健康监测数据的重要因素之一。在处理温度效应时,通常通过小波分解、小波重构将低频的温度效应进行剥离,对剥离后的作用效应进行深入分析,而剥离的温度效应作为冗杂数据不做处理。桥梁的纵向变形(支座顺桥向)受活载影响极为微小,其纵向位移响应主要受桥梁温度作用的影响。由于温度作用和作用效应(纵向位移)之间有显著的非线性关系,当前健康监测变形测量预警仅仅是设置最大值最小值进行预警,而单一的极值并不能准确反映桥梁伸缩缝和支座工作状态是否正常,作用和效应的非线性关系又使得二者间联系难以准确表达。
1 纵向变形与温度统计分析
桥梁健康监测系统中,各个响应都是外界作用(环境、荷载等)激励所产生的,各个监测要素具有普遍的联系性。把握好数据的关联性,能更好地识别数据异常,了解桥梁内部变化,对桥梁进行科学地评估,对预警设置进行合理地优化。
1.1 相关性分析
相关分析是在分析两个变量之间关系的密切程度时常用的统计分析方法。简单来说,相关性可以分为正相关(变化一致)、负相关(变化相反)、无相关(没有明显依存关系)三种。两个变量的相关性可以用相关系数表示,相关系数的绝对值越接近1,说明两个变量之间的相关性越强。
青银线济南黄河大桥是独塔双索面扁平钢箱梁斜拉桥跨径布置为60 m+60 m+160 m+386 m,以大桥2 月份崔寨侧支座位移数据对环境温度数据进行关联系分析。通常认为结构的温度和温度变形间存在线性关系,选择崔寨侧(56 号墩)上下游两个纵向位移计(DSP-Y-17-1~2)进行分析,见图1。通过线性回归分析可知,支座位移和环境温度有较显著的相关关系,见图2、图3。两个位移计和温度间的相关系数(R)均在0.95 以上,其数据间相关性较强,左右两侧回归系数和相关性也较为接近。
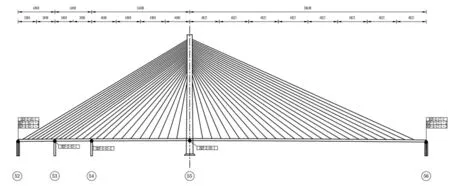
图1 结构位移监测系统
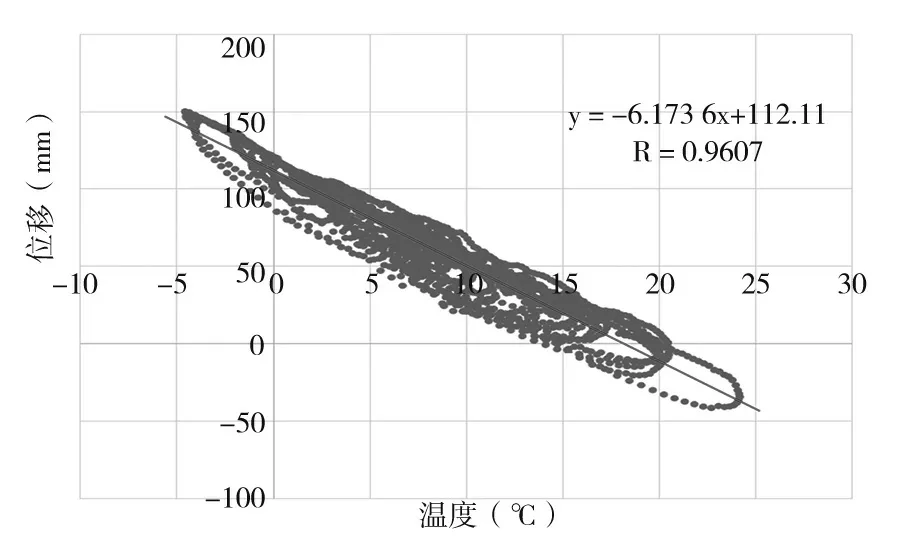
图2 DSP-Y-17-1 位移计随时间变化
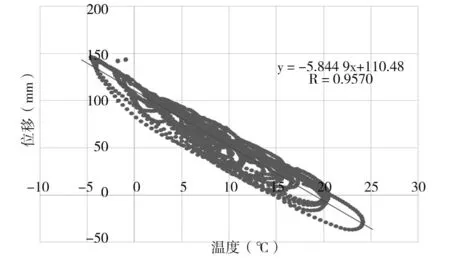
图3 DSP-Y-17-2 位移计随时间变化
1.2 周期性分析
分析可知气温和位移间具有较强的线性关系,此外,气温的日变化与年变化是与太阳辐射相联系的一种周期性变化。气温一天中有一个最高值和最低值。日出后,随着太阳辐射增强,温度升高,由于地面热量传递给空气需要一定时间,所以气温的最高值通常出现在14 ∶00 左右,随后气温逐渐下降,在日出前的4 ∶00—5 ∶00 达到最低温度。与气温线性相关的位移值变化也应具有相似的关系,选取温度变化平稳的5 d 进行分析,见图4、图5。
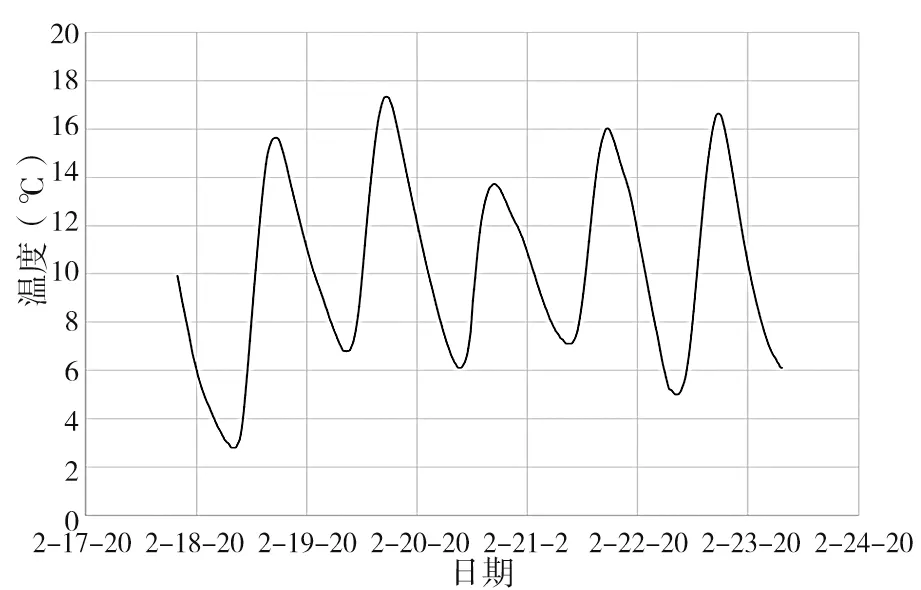
图4 温度随时间变化(5 d)
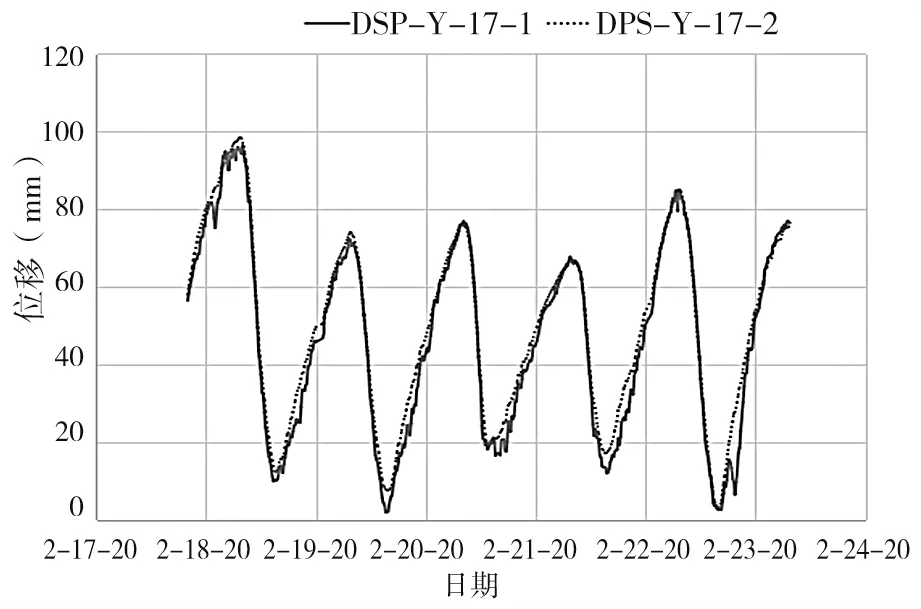
图5 位移随时间变化(5 d)
图4、图5 均为采样频率为15 min 采集一次,形成有限长度的序列。可以看出温度、位移随时间变化的序列均具有一定的周期性,但又非严格的周期性序列。周期性信号x(n)通过离散傅里叶变换可以得到频谱密度x(k)。通过离散傅里叶变换可将上述温度和位移的信号由时域转换为频域,进而分析温度和位移的周期特点。

式中:x(k)—离散傅里叶变换后的数;x(n)—采样的信号,温度或位移;n—采样所得数据序号,n=;Ts—采样间隔;t—采样时间,s;N—总采样数量;k—频率,Hz。
对温度、位移曲线分别进行离散傅里叶变化,得出功率谱密度见图6 ~图8。 温度位移变化频率和周期见表1。
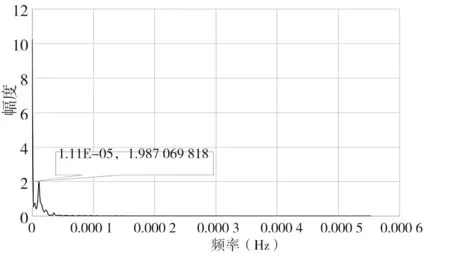
图6 气温变化频域
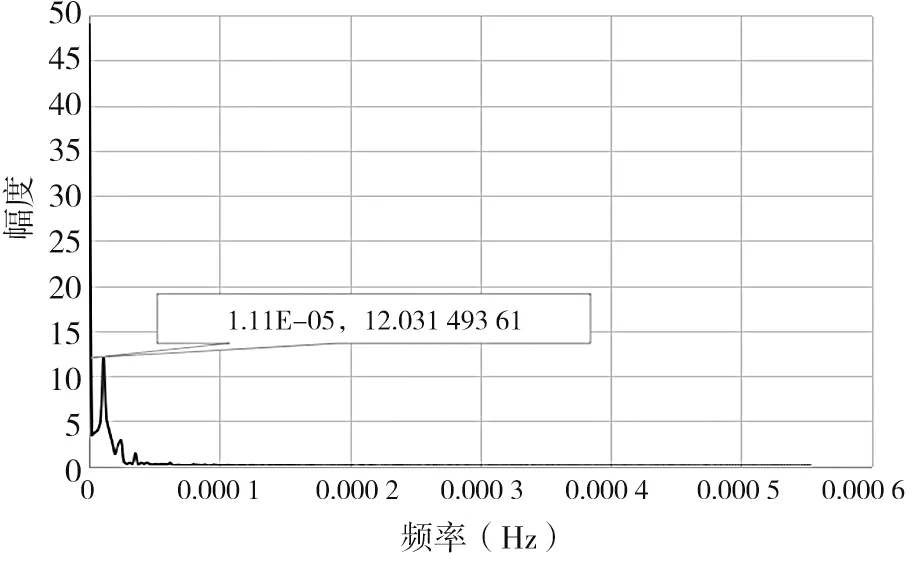
图7 DSP-Y-17-1 支座位移变化频域
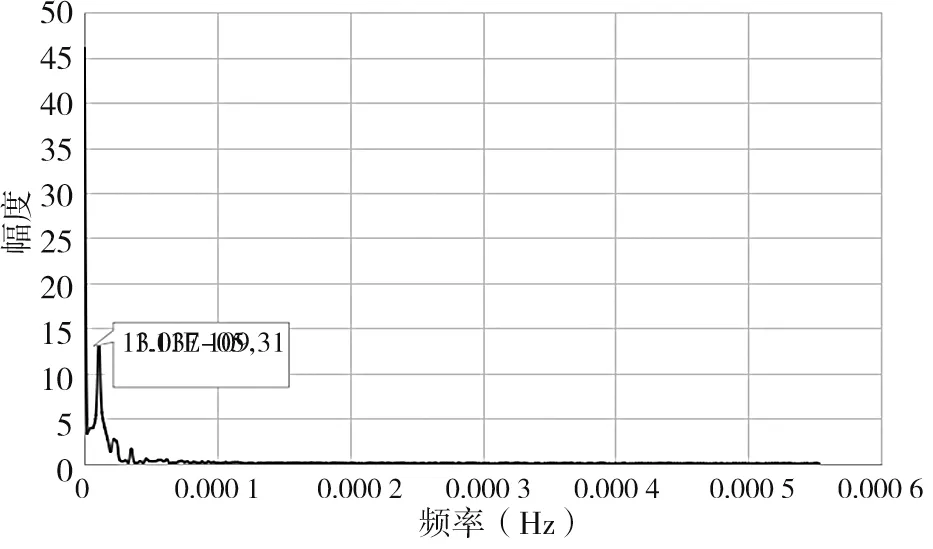
图8 DSP-Y-17-2 位移变化频域

表1 温度位移变化频率和周期
由表1 可知,环境温度具有较强的周期性变化趋势,周期约为1.04 d。受温度影响,两个位移计采集的数值也呈周期性变化,变化周期与温度变化周期相同,约为1.04 d。
2 温度作用时滞效应
2.1 时滞效应
由分析可知,温度与支座位移间有较强的相关性。用回归曲线分析判断其余时段数据时,发现回归曲线拟合所得位移与实测数据相差很大,无法用于判断支座位移是否正常。见图9,取5 d 数据,根据线性回归方程进行比较,二者最大偏差约33.49 mm,而当天位移计测得最大温差所产生的位移约为80 mm,无法用于判断桥梁支座处位移是否发生异常。
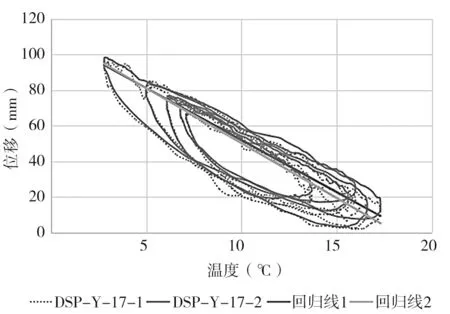
图9 位移温度线性回归拟合比对(5 d)
分析可知,温度、位移变化具有一定的周期性,而对于一般的周期函数均用公式(2)进行表述,对于正弦波振幅Y,角速度ω,初始相位θ 缺一不可,不同相位决定了波的起始位置不同。由图9 可得温度和位移的变化呈椭圆形变化,说明位移变化相较于温度变化相对滞后,即温度和位移间存在时滞效应。时滞效应的本质是由两个关联参数的弦信号间的相位差造成的,相位是指一个波某个特定的时刻在循环中的位置,是判别信号在波峰、波谷或它们之间的某点的标度。相位差会使得类弦曲线信号成椭圆形变化。

式中:t—时间,s;ω—角速度;A—最大振幅;Y—振幅;θ—初始相位。
2.2 相位谱
通过离散时间傅里叶变化获取温度和位移的频率-相位图谱,进而分析其相位差和时滞效应。

式中:Im[X(k)]—傅里叶变换后实部;Re[X(k)]—傅里叶变换后虚部; (k)—相位谱函数。
根据式(3)求得温度、DSP-Y-17-1~2 的相位谱函数曲线,见图10 ~图12,分析两者间的相位差并消除,可提高温度和位移间的相关性。
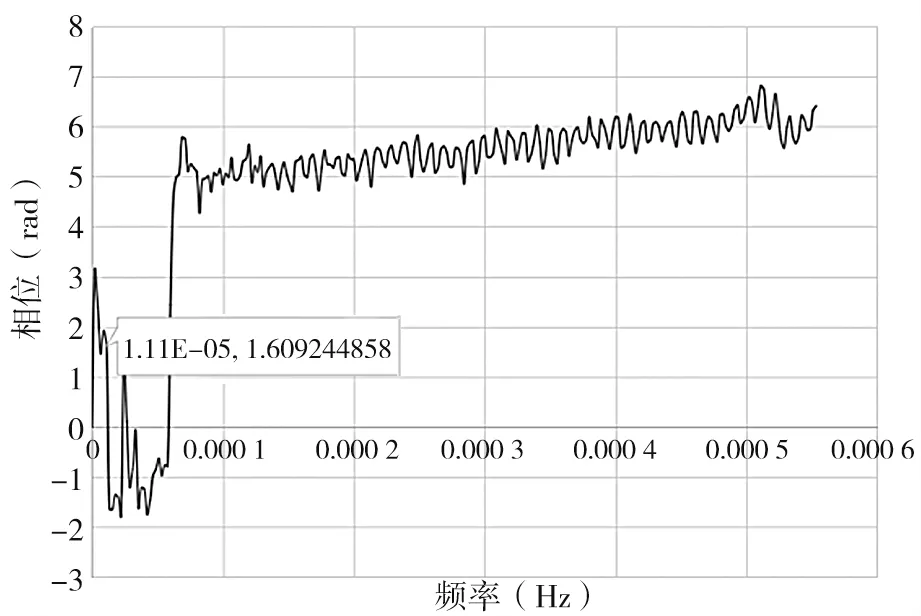
图10 温度相位谱曲线
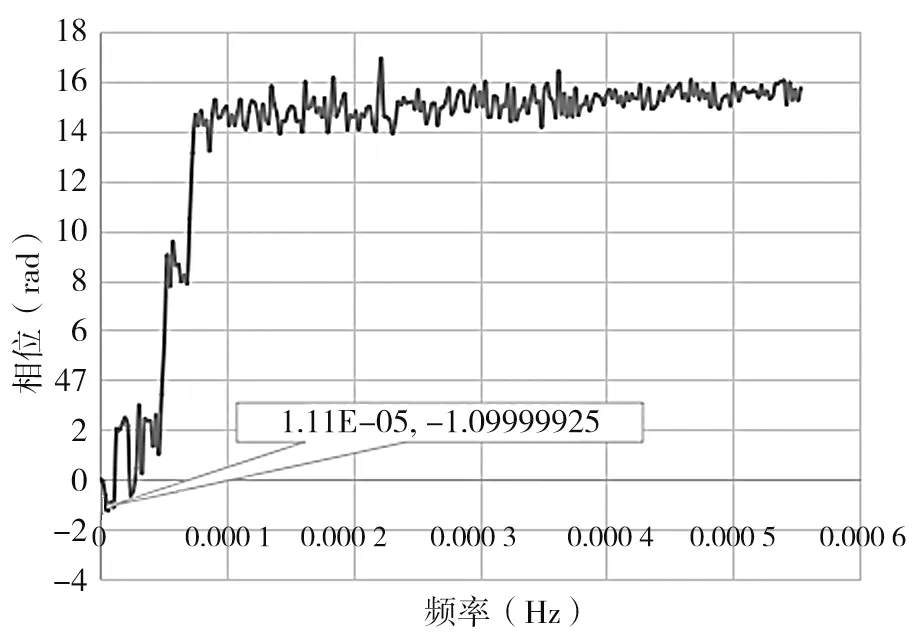
图11 DSP-Y-17-1 位移计相位谱曲线
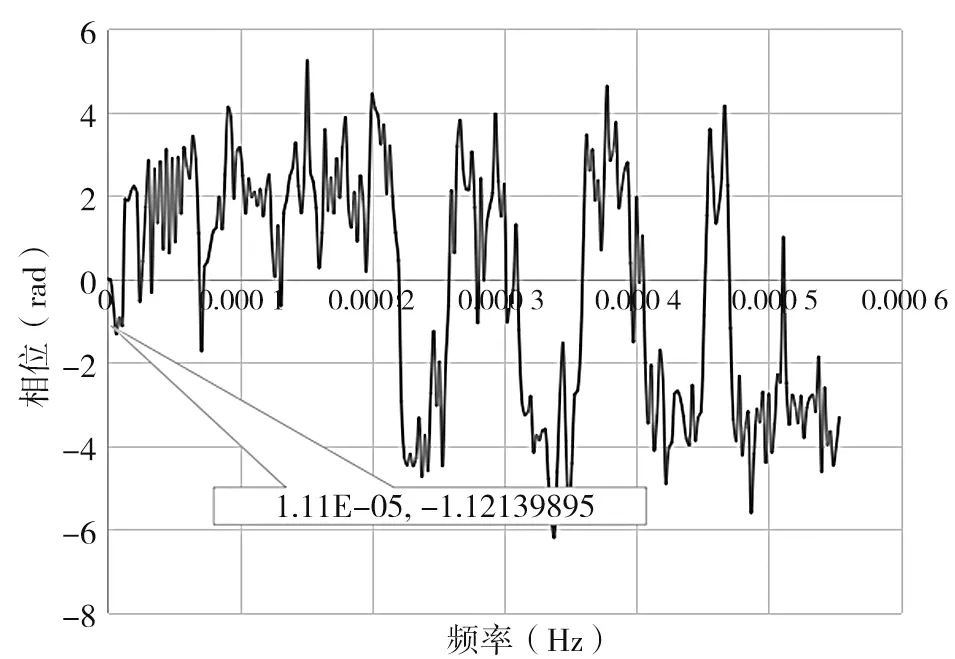
图12 DSP-Y-17-2 位移相位谱曲线
经计算,当频率为1.111 1×10-5Hz 即周期为1.041 7 d 时,温度初始位移为1.609 2,DSP-Y-17-1位移计为-1.100 0,DSP-Y-17-2 位移计为-1.121 4。

表2 温度和位移的初始相位
分析可知该桥温度和位移成负相关,结合初始相位换算成时间可得,纵向位移和温度滞后关系,DSP-Y-17-1 位移计滞后1.65 h,DSP-Y-17-2 位移滞后1.57 h。
2.3 相关性修正
对数据进行相位修正,可以消除时滞效应对健康监测数据的影响,使得离散数据得以收敛,提高数据间的关联性。对位移数据平移修正后结果见图13、图14。

图13 DSP-Y-17-1 位移温度随时间变化(修正后)

图14 DSP-Y-17-2 位移温度随时间变化(修正后)
由表3 回归分析结果可知,进行平移后温度和位移的线性关系更加明显,相关性得到显著提高,两侧数据回归系数更相近,数据更加收敛。由于该桥中间跨支座未装纵向位移计,无法准确推算出其线膨胀系数,无法进一步验证该修正方法。

表3 温度位移线性回归分析结果
3 结语
(1)通过傅里叶变换对支座位移和温度作用进行分析,得到其周期、相位、幅值的特点。(2)通过对青银线济南黄河大桥支座位移和环境温度数据进行分析,得到桥梁的支座位移和温度变化间具有极强的相关性,其位移变化周期和日气温变化周期一致。环境温度和支座位移间存在时滞效应,支座位移较环境温度滞后1.5 h。(3)通过数据相位平移,修正后的位移数据和环境温度呈线性相关,相关性极大提高,数据间关系也更加收敛。

