新型电子变极式五相永磁电机的优化设计

朱敬民，张玉峰

(佳木斯大学 信息电子技术学院，佳木斯 154007)

0 引 言

多相电机以其转矩密度高、功率密度高和容错能力强等优点，在电动汽车领域得到了越来越广泛的关注和研究[1]。

基于矢量解耦控制，通过注入非正弦波电流，多相永磁电机可以获得与三相直流无刷电机相同的转矩密度，而且转矩脉动更低[2-3]。由于具有更多相冗余设计，多相电机的另一个重要特点是容错能力强[4]。在开路故障时，相比于传统的星形连接的三相电机，多相电机不需要改变硬件连接，仅需改变控制算法，就可以维持一定的输出能力[5]。此外，通过注入高次谐波电流，可以获得电子变极的效果[6-7]。例如，注入基极电流时对应p对极工作模式，而注入三次谐波电流时对应3p对极工作模式，从而可以通过控制一次和三次谐波电流的注入比改变电机的输出性能。这样，当逆变器输出电压饱和时，为进一步扩展电机的运行范围，弱磁不再是唯一的解决方案。传统变极调速是通过改变定子绕组线圈的连接方式使电机工作在不同的极对数模式下，以满足低速大转矩和拓宽恒功率运行范围要求，但这种方法的缺点是需要停电切换，切换过程中不输出转矩，且切换过程不连续、不平滑，会产生冲击电流和冲击转矩[6]。传统多相永磁电机三次谐波反电动势含量较低，只是利用高次谐波电流的注入增加输出转矩，不能真正实现电子变极的效果。本文的新型五相电子变极式永磁电机的基波和三次谐波反电动势所含比例同样重要，可以实现真正的多控制自由度，达到变极的效果。该原理也在文献[8-9]中得到了验证。与传统变极方法相比，无需绕组切换技术[10]和辅助转换器即可改变工作极性，因此新型电子变极式电机扩展运行速度范围的方式更为高效。

本文首先研究了新型电子变极式类电机分数槽绕组的设计方法；其次，对表贴式永磁体的形状进行优化，以适应所选择的绕组结构；然后，通过最大转矩电流比控制策略研究了整个转速范围的速度-转矩特性，并与经典的三相正弦波表贴式电机进行了比较。

1 绕组结构选择

分数槽集中绕组具有制作简单、绕组端部短的优势，在工业应用中应用广泛，特别适用于对使用空间要求较高的混合动力汽车用电机。在这一部分中，我们使用了两个标准来选择分数槽集中绕组的结构：(1) 基波和三次谐波的绕组因数；(2) 磁动势的空间谐波分布。

1.1 绕组因数计算

根据绕组函数理论，每个谐波绕组因数可以由绕组的分布矩阵计算得到，如式(1)所示[7]。根据分布矩阵的一列即可计算出所有电流谐波的绕组因数。

(1)

式中：m为相数；Qs为槽数；p为极对数；di,n为分布矩阵中第i行和第n列的值。对于任意的m/Qs/p组合，无需画出对应的槽电动势星形图，即可快速、简便地计算绕组因数。

本文用式(1)计算了五相电机绕组不同槽/极数组合时的绕组因数，如表1所示。表1中下划线数值对应三次谐波的绕组因数。关于分数槽集中绕组槽/极数组合的研究也可以在文献[7，11]中找到。为了设计双极性五相电机，在选择槽/极数组合时必须同时考虑到基波和三次谐波的绕组因数。五相绕组组态选择20槽8极，其基本绕组因数k1=0.588，三次谐波绕组因数k3=0.958。根据绕组因数的数值，15槽14极和20槽18极的组合似乎更合理，但由于这些组合的磁动势空间谐波含量丰富，因此不会选择。

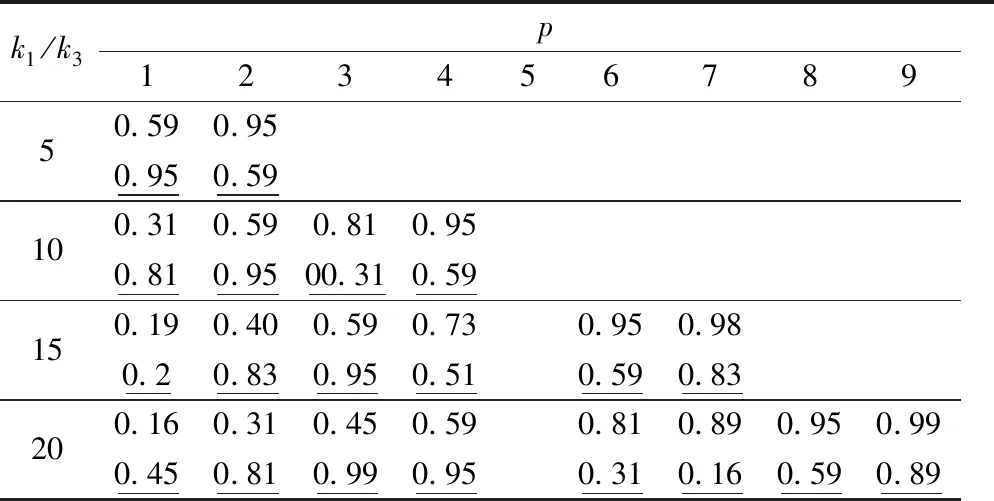
表1 五相电机的绕组因数

1.2 磁动势分析

某相的绕组函数对应于该绕组注入1 A恒流时的绕组磁动势[12]。它表征了绕组空间磁动势的分布，而时间分布是由通入电流随时间的变化决定。通过计算各相的绕组函数和定子电流的输入，可以计算出合成磁动势。它等于绕组函数与电流的乘积，即：

(2)

式中：Nn(θs)是第n相的绕组函数，是空间位置角θs的函数；in(t)是第n相注入的电流。

考虑所有电流谐波h(如五相电机的基波和三次谐波)，则前式：

(3)

式中：Ih是h次谐波的电流幅值；ω是角频率。

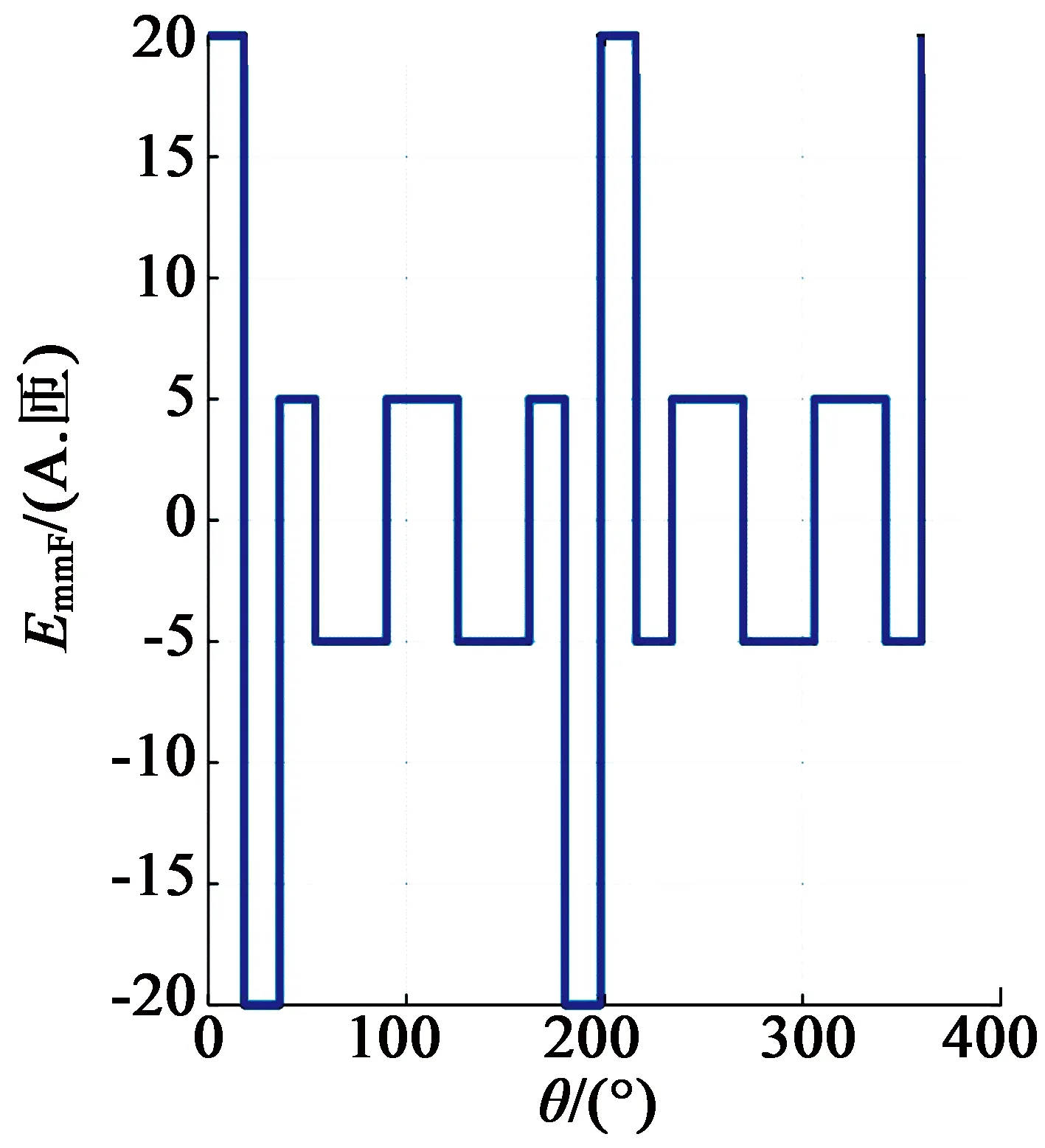
然后，以表1中具有较大的绕组因数值的两种组合为例，通过注入基波电流和三次谐波电流来分析其磁动势分布及其空间谐波频谱。图1显示了五相20槽18极组合的分析结果。尽管该组合的基波和三次谐波均具有较大的绕组因数，但也富含磁动势非工作谐波，从而会导致转子铁心及永磁体中产生涡流损耗，严重时会造成永磁体退磁，降低电机的性能。

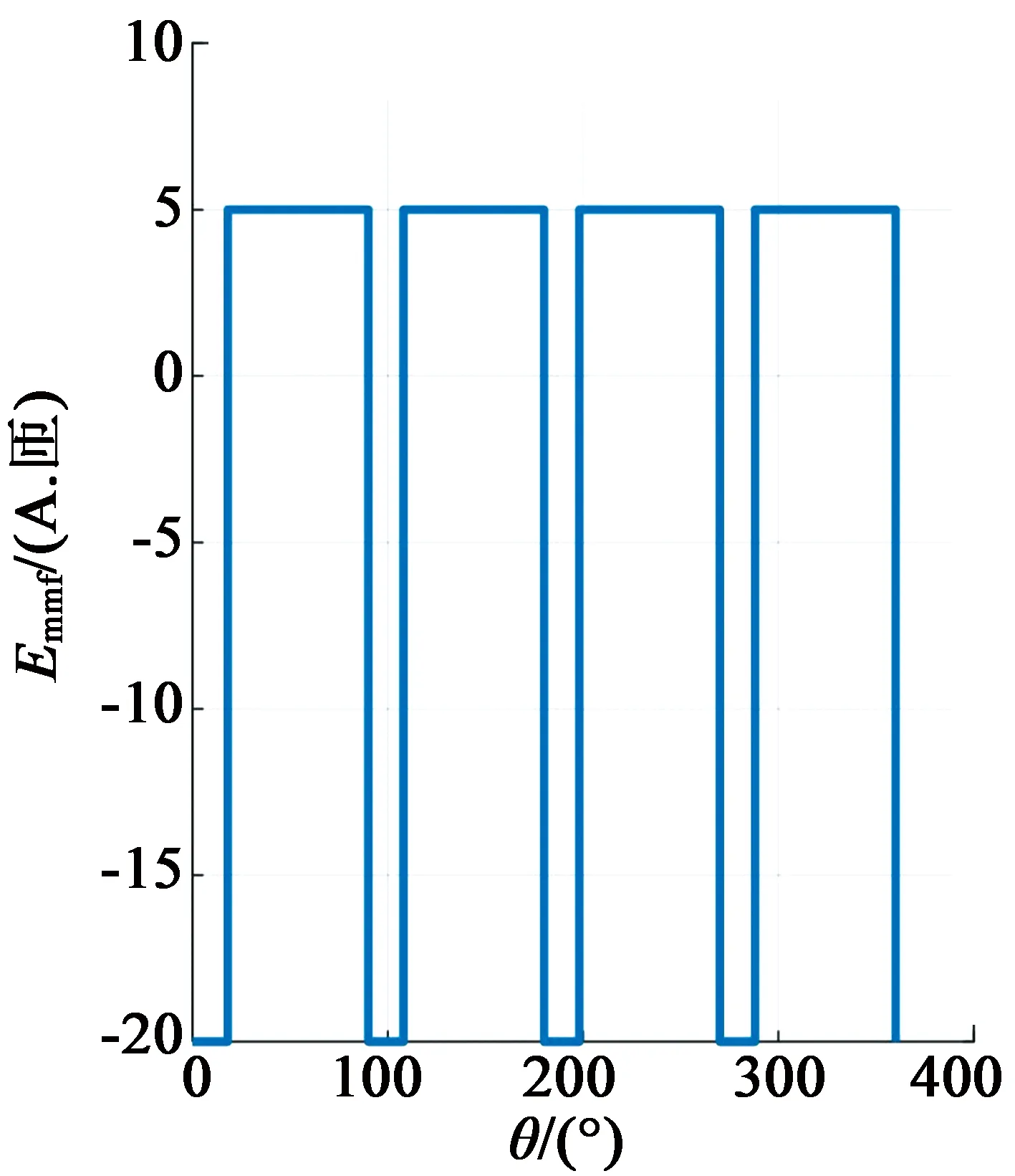
图2显示了五相20槽8极的磁动势分布，其每极每相槽数(Spp)为0.5。由图2可知，通入基波电流时，工作谐波为4，对应4对极工作模式，磁动势谐波含量较低，因此涡流损耗较低[13]。当注入三次谐波电流时，工作谐波为12，即电机工作在12对极模式下。需要指出的是，注入基波电流和三次谐波电流，在五相电机中形成的旋转磁场的转速是相同的，因此当同时注入基波和三次谐波电流时，电机的输出转矩是二者之和。电动汽车用电机要求低速时具有大转矩，高速时恒功率运行范围广，因此，该新型电机在低速运行时，主要工作在3×4对极模式，高速运行时工作在4对极模式。这种工作效果可以通过控制注入基波和三次谐波电流的比例获得，即达到电子变极的效果。

上述对磁动势分析可以通过有限元分析方法验证。图3描述了有限元模型中气隙磁通密度的波形及其谐波分析。在有限元模型中删除了永磁体。由图3可知，与磁动势分析结果一致，验证了该方法在磁动势计算的有效性。

2 转子结构设计

对于给定的绕组槽极数组合，注入三次谐波电流提高输出转矩的效果与Brotor3/Brotor1的值有关[7]。该比值主要取决于转子永磁体的几何形状设计。本部分的研究目的是根据选定的绕组槽极数组合，设计合适的转子永磁体形状，获得最大输出转矩。为了简化分析，做出以下假设：(1) 忽略饱和效应；(2) 无齿槽效应；(3) 永磁体之间无漏磁。

2.1 永磁体形状设计

双极性电机的特殊性是注入基波电流或三次谐波电流能够产生数值大小相当的转矩值。因此需要设计永磁体形状，使得基波E1和三次谐波E3电动势的数值大小相当。对于任意谐波h，其反电动势的表达式可由式(4)给出：

eh=2lNphRrotorωrkhBmh·sin(hpωrt)

(4)

式中：h为谐波阶数；l为电机轴向有效长度；Nph为每相匝数；Rrotor为转子半径；ωr为转子的机械角速率；kh为第h次谐波的绕组因数；Bmh为剩磁。

因此，对于给定几何形状的电机，电动势与绕组因数以及永磁体形状有关。假设气隙磁通密度仅包含基波和三次谐波分量。

Bg(θs)=Bm1sin(pθs)+Bm3sin(3pθs)

(5)

为了提高三次谐波的反电动势值，使得E1=E3，可通过式(4)、式(5)获得以下关系。

(6)

理想情况下，永磁体厚度与气隙通量密度之间的关系可以表示：

(7)

式中：le为永磁体与气隙的总长度；Br为剩磁。

根据上述分析，可以确定图4(a)的特定梯形磁体形状，达到增强三次谐波磁通密度的效果，从而提高输出转矩。图4(b)和图4(c)给出了新型5相20槽8极双极性电机的空载电动势及其谐波分析，该结果通过有限元分析进行了验证。

(a)

(a)

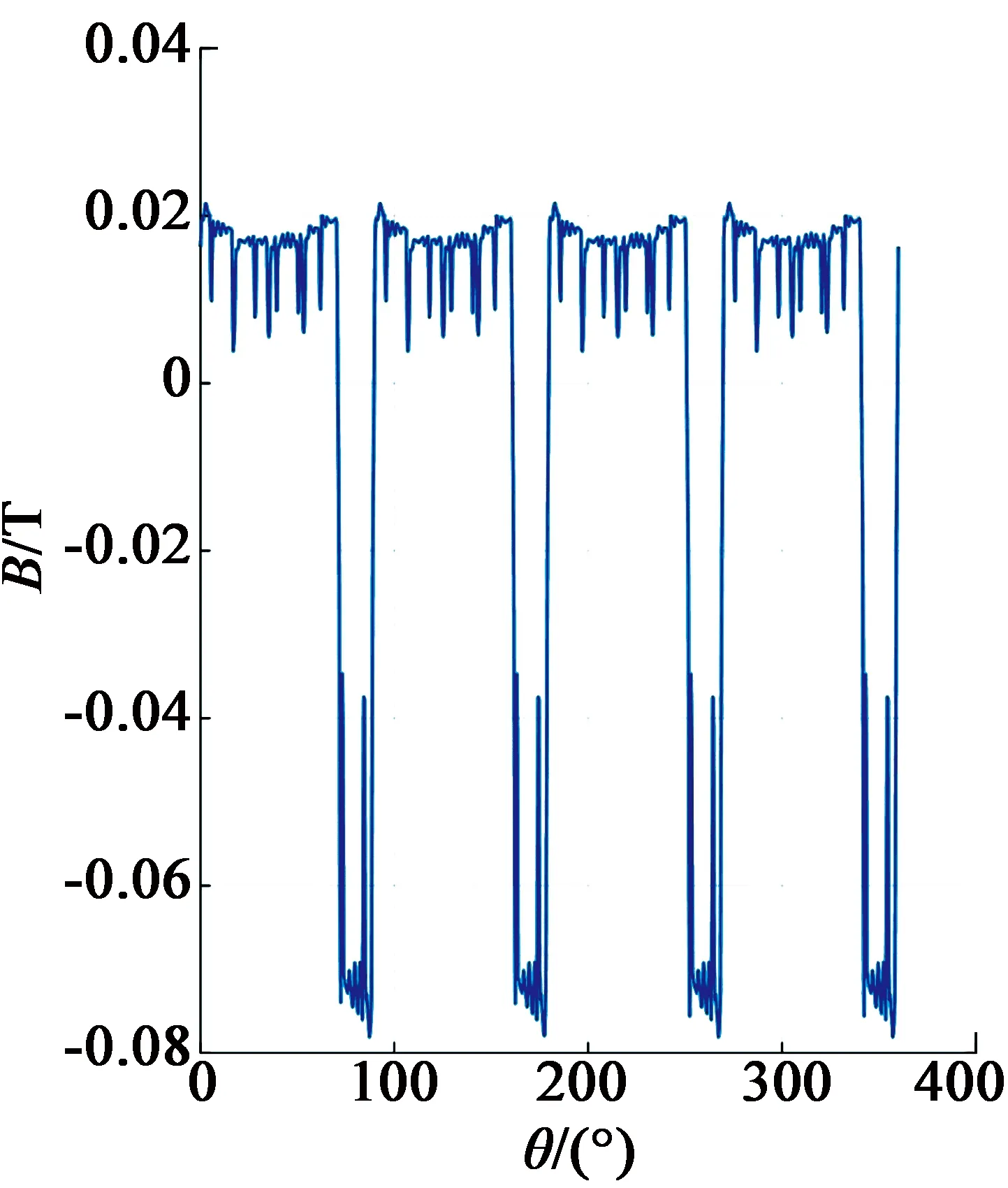
(a) 气隙磁通密度的波形

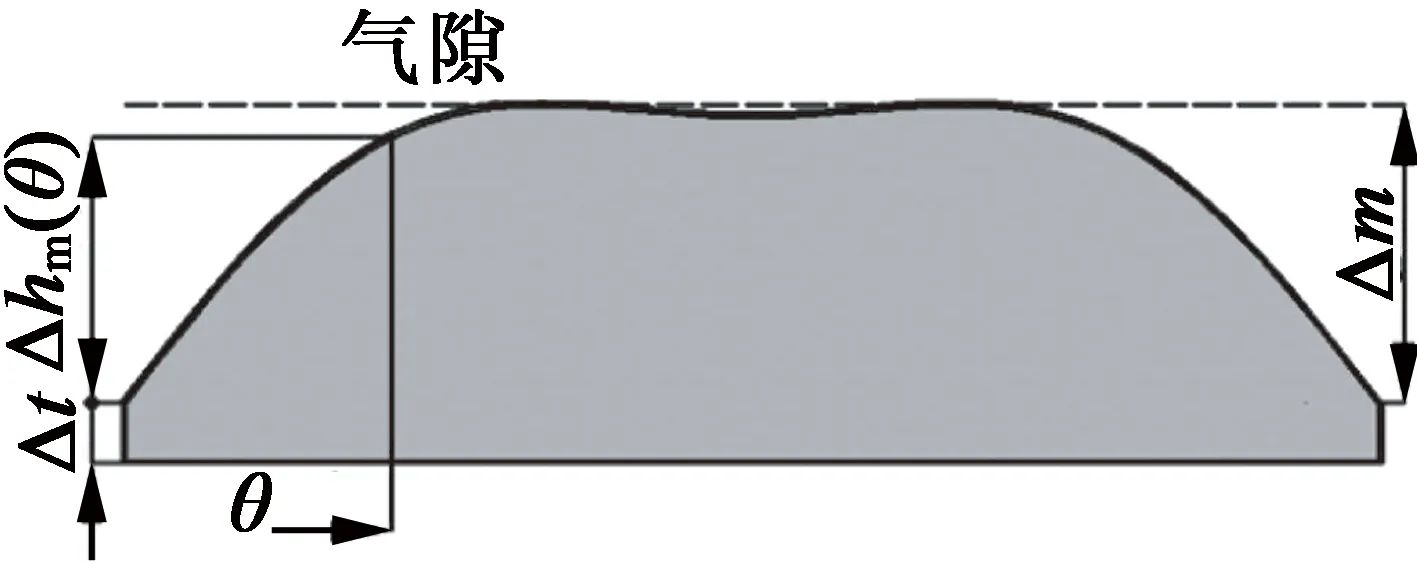
(a) 磁体形状

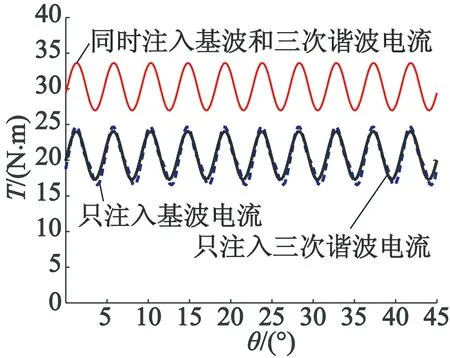
图5 采用有限元法的三种电流下的转矩输出

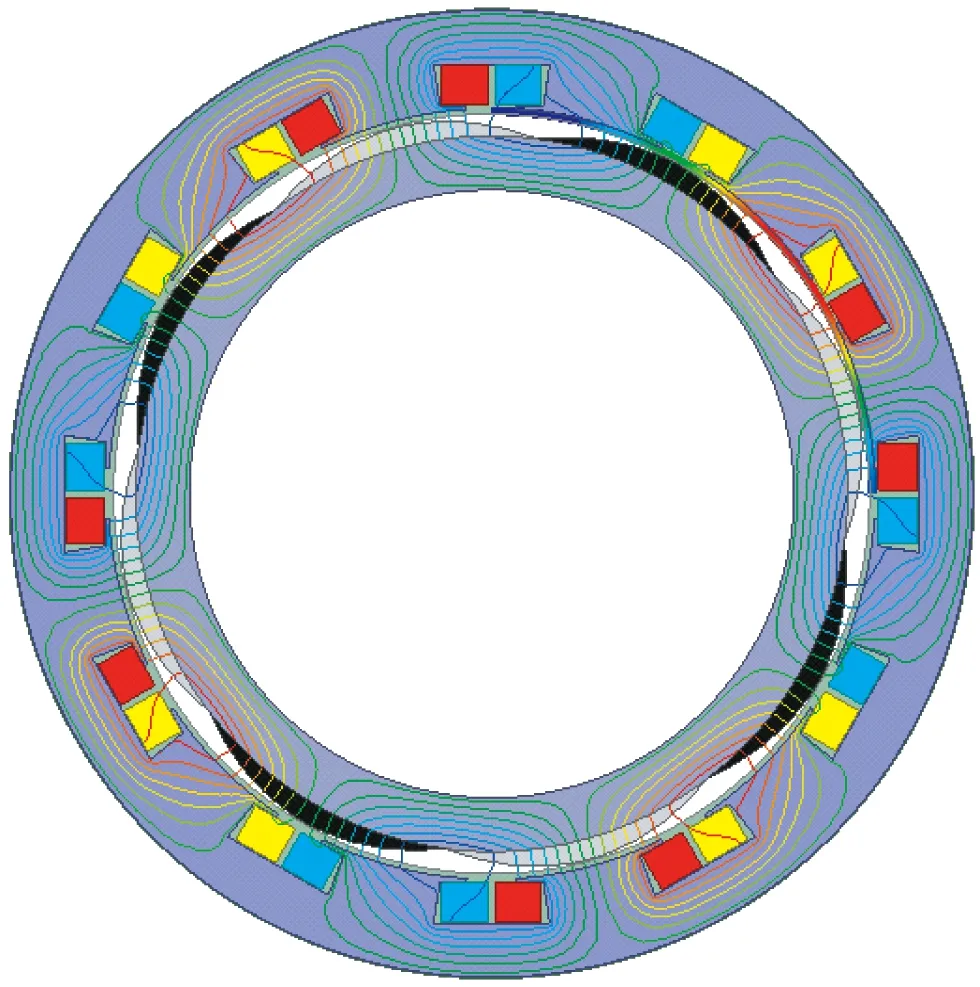
(a) 等效三相电机

2.2 边缘厚度选择

图4(d)显示了不同磁体边缘厚度Δt时，有限元模型得到的气隙磁通密度分布。可以看出，在保持磁体的总高度恒定的前提下，磁通密度的基波增加而三次谐波减少。另外，在Δt=0.5 mm时，磁通密度的畸变具有最小值。因此，选择了具有最小总谐波失真(THD)的边缘厚度Δt，即0.5 mm进行进一步研究。

2.3 使用最大转矩电流比控制加强扭矩

在五相电机中，由基极电流和三次谐波电流产生的电磁转矩可表示：

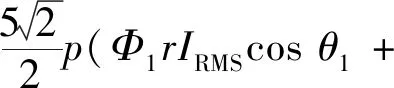
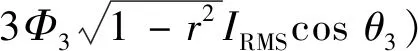
(8)

式中：I1,I3为基极电流和三次谐波电流的峰值；Φ1,Φ3是基波和三次谐波磁通量的峰值；IRMS是注入定子中电流的有效值。

(9)

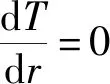
(10)

对于给定的电流有效值，图5给出了最大转矩电流比控制策略在三种电流注入下的输出转矩，只注入基波电流，只注入三次谐波电流，同时注入基波和三次谐波电流。事实证明，注入三次谐波电流不仅可以提高输出转矩，还可以改变电机的极性，从而扩大了转速范围。因此，设计的有效性得到了验证。

3 与等效三相电机的比较

3.1 等效三相电机的结构

为了进一步证明双谐波电机电子变极的效果，对五相20槽8极双谐波电机和等效的三相12槽8极电机的性能进行了比较。为了等效地比较两台电机，在设计等效的三相电机时要考虑如下因素：(1) 三相电机的极数与五相的极数相同；(2) 修改三相电机的槽数，使之与三相电机绕组保持一致，并保持与五相电机相同的Spp=0.5；(3) 在两个电机中，气隙通量密度幅度保持相等。图6给出了三相电机和五相电机磁力线分布图。

3.2 性能比较

根据控制策略评估两台电机的性能，其目标是找出在电压和电流限制下电机所传递的最大扭矩[8]。图7为三相和五相电机的转矩-速度曲线的对比。低速时，三相电机的输出转矩较高，这是因为五相电机气隙磁密较小导致的。但是，五相电机最大运行速度要高很多，与三相电机相比较，双极性五相电机适合于高速运行的场合。

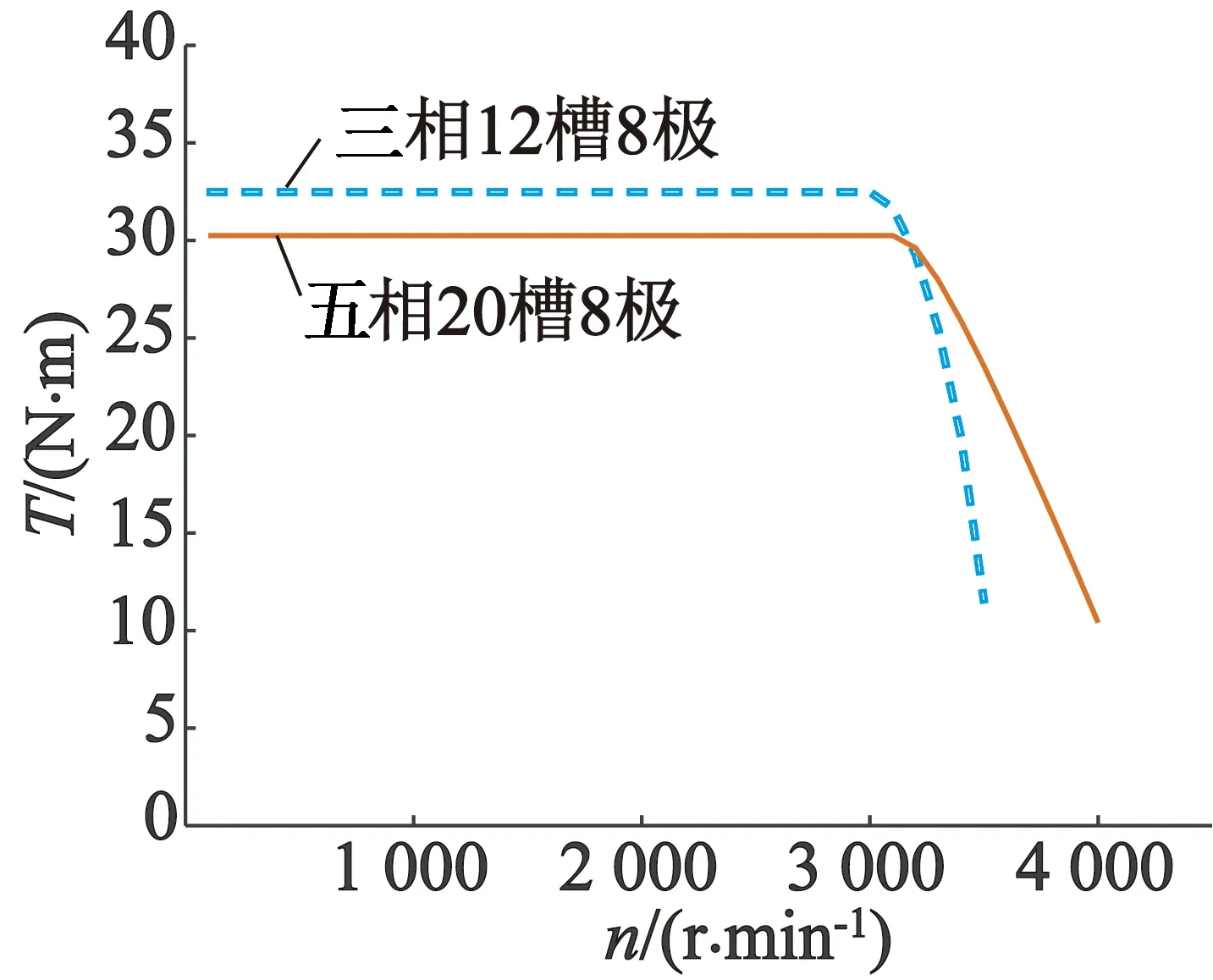
图7 三相和五相电机的输出转矩对比

4 结 语

本文研究了一种新型电子变极式五相永磁同步电机，给出了此类电机的设计考虑因素，包括定子绕组和转子永磁体形状的设计。然后在最大转矩电流比控制策略下通过三种供应的输出扭矩来验证所提出电机的特殊性。所有分析结果都通过有限元分析进行了验证。