基于GPU的拉格朗日乘子优化动态经济调度

李 源，初 壮

(1.云南电网有限责任公司大理供电局，云南 大理 671000；2.东北电力大学，吉林 吉林 132012)

近年来，风力削减相关的问题[1-2]在电力系统中已备受关注。为了减少缩减风电[3]，调度方案需要进行相应的调整。调整后的计算必须具有更高的效率，并且成本很少。调度方案的调整针对整个调度和调度周期的各个部分。调度周期的各个部分需要在满足系统的约束条件下进行机组的微调，调整将在一些连续的时间间隔内进行，并且不会启/停发电机，它可以被制定为大规模，连续和非线性的优化模型，这与传统的动态经济调度(DED)相同。

非线性编程方法，如二次规划[4]、班德斯分解[5]和内部方法[6-7]，常用于求解类似DED典型的非线性优化问题；同时，随机优化方法，如遗传算法[7]、进化规划和粒子群优化[8-9]，也被用于求解DED模型。这些方法的实现都为串行计算，它们适用于当时的硬件和软件环境。并行计算技术近年来发展迅速。计算机统一设备架构(CUDA)、基于图形处理单元(GPU)是一种高效、低成本的并行计算技术，使用CPU的“中央处理”向CPU和GPU并用的“协处理”发展，已应用于电力系统[10-11]。在文献[10-12]中，用于求解功率流问题的牛顿-拉普森方法在GPU上实现，雅可比矩阵、LU分解和前车回代在GPU上实现；文献[12]提出了一种GPU加速解决方案，它在分批处理ACPF(alternating current power flow,交流潮流)之间创建了一个额外的并行层，从而实现了更高水平的整体并行性。

本文基于GPU的拉格朗日乘子优化建立了DED模型，引入并行计算加速求证过程，下面逐一进行论述。

1 研究问题模型

考虑风电入网的电力系统调度模型，与常规经济调度不同点在于：电力系统经济成本的目标函数；风电出力的上下限约束；电力系统的功率平衡约束。

1.1 目标函数

在常规能源达到限值时，风电的引入能增加系统韧性，从而减少弃风量。风电入网后[9]，电力系统的经济目标函数如下：

minZ=E1+E2

(1)

式中：E1表示常规火电机组的费用，包括运行成本、开启停成本；E2表示风电机组的发电成本。

火电发电成本包括：燃料成本和开启停成本，具体表达形式如下:

(2)

(3)

式中：T代表T个调度周期；PWt为在第t时段风电出力；F(Pit)为第i台机组第t个调度周期的运行成本；SUit、SDit分别为常规机组i在t时段的开启停成本；CW为风功率的成本系数。

常规机组的开启停成本为:

SUit=CU×Iit×(1-Iit-1)

(4)

SDit=CD×Iit-1×(1-Iit)

(5)

式中:CU、CD分别为常规机组开机和关机成本系数;Iit为第i台机组在第t个调度周期的机组状态，取“1”时表示机组开机，取“0”时表示机组关机。

1.2 约束条件

a.负荷平衡约束。在考虑风电的并入和不计网络损耗的情况下，机组的发电量并入风电量后PWt和负荷Pbt相等：

(6)

Pother=PLianluo+PHedian+PGuangfu+PShuidian

(7)

式中:Pbt为电力系统在t时刻段内的负荷值;Phdit为第i台火电机组在第t时段的功率；PLianluo为电力系统的联络线功率;Pother为其他功率，包括核电功率PHedian;光伏功率PGuangfu;水电功率PShuidian。

b. 系统旋转备用约束。为保证电力系统的安全运行，在风电入网后，电网需要使所有常规机组和其他并网能源之和满足一定的限制，具体如下：

(8)

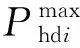
c.机组功率限制约束。对于常规火电机组，需要在每个时刻都得满足最小、最大出力约束；对于电网并入风电后，风电入网功率也应小于等于此时的风电集群总容量qwt，具体表达为：

0≤PWt≤qwt

(9)

(10)

2 基于GPU的拉格朗日乘子优化

2.1 GPU并行计算架构

单指令多线程(SIMT)是基于GPU的CUDA提供的计算的显著特征，其与多指令多数据(MIMD)明显不同。 在GPU内部，八个或更多流处理器(SP)连接到流多处理器(SM)，每个GPU由许多SM组成，通常情况下，每个SM中包含32(或48)个流处理器(SP)。SP是GPU上数据处理的最基本单元。GPU计算平台架构含有两台2.40 GHz的英特尔 Core i7-4700HQ处理器，每台处理器的CPU含有6个核心(core)。GPU和CPU通过外围部件互联(PCI)总线相连。GPU的型号为NVIDIA GeForce GT 745M。

一个程序的并行实现包含两部分：CPU执行(host)端和GPU执行(device)端，见图1的CUDA计算模式，其中kernel为在GPU上执行的程序，GPU执行端可使用信息多点传递接口(MPI)等技术并行。

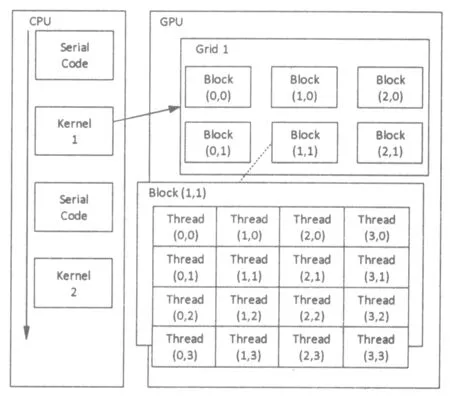
图1 CUDA计算模式

在SIMT中，每32个线程被调度为线程warp并同时工作，其中warp表示NVIDIA的线程粒度，为线程的集合。如果可以将问题划分为可以独立解决的粗略子问题，则可以通过GPU内任何可用多处理器上的线程块并行地求解。当子问题的数量巨大时，基于GPU的并行计算比传统的基于CPU的串行计算花费更少的时间。例如，在雅可比矩阵和海申矩阵的每个元素最优求解中，可以采用GPU并行计算。

2.2 算法实现

本文中的拉格朗日乘子法包含了大量的向量运算，例如有关前后两个时刻的功率的变化关系为例，P(k+1)=P(k)+ΔP，这里的P为n维矢量。在CPU上，传统的实现方法如下：

(11)

当循环变量i从0增加到n，功率向量的对应元素按照顺序进行加运算。但是在此过程中，每一组元素的计算过程是独立的，只有在计算完PW时才会计算PW+1，彼此没有相互的依存。GPU中，上述的循环运算可以在一条流水线Block中同时完成对P1,P2,…,PG的求解。

(12)

采用基于GPU的并行计算来加速优化。式(12)可以以向量P的每个元素的形式重写如下：

(13)

由于这里需求解的机组功率为N×T的二维矩阵，其中N表示机组总数量。要实现并行运算，可将上式先转为单台机组，化简为：

(14)

其中，sum1代表机组1等式约束的数量，sum2代表了机组1不等式约束的数量。

相对于机组的单个求解，由于每个机组的参数是固定的，所以在时间不同的时候，式(13)的表达形式是一样的，假设系统总周期为T。为了对这T个未知量迭代求解，可以取T个Block作为一条流水线。再扩展到G台机组，便为G条流水线。将式(15)展开，可得出具体的迭代表达式如下，同样式(16)也为P1流水线所执行的指令过程。

(15)

(16)

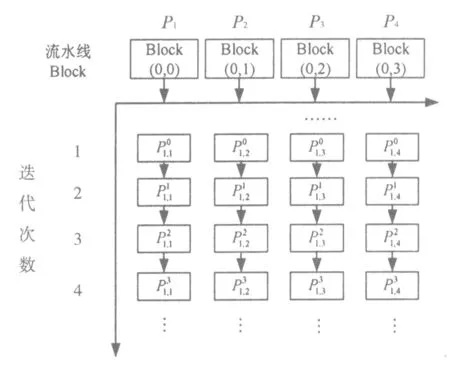
图2 流水线迭代序列

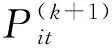
2.3 更新不等式约束乘子的过程

至于不等式约束，它对于方程(8)-(9)具有不同形式来讲有些复杂。SIMT并行计算只能处理具有相同形式的约束，因此，更新μ(k)的过程应该分成几个单独的子程序，每个子程序对应一种形式的约束。

机组的上下限约束，即方程式(9)，不需要通过拉格朗日乘子来处理。如果某个变量的值超出了它们自身的范围，则应将其值固定在超出的上限/下限边界上。它可以通过简单的Kernel函数来完成。

方程式(8)和(9)分别是斜坡约束和旋转储备约束。它们具有相似的形式，每个表达式都包含两个约束。例如，如果i和t是已知的，则式(8)可以等效为：

(17)

(18)

但是，两个约束及其乘子应该在相同的Kernel函数中计算。并且在函数中，两个约束和乘子是串联计算的。不等式约束多出现一个，在实现中也会多出一个线程执行。

3 算例分析

3.1 方案制定

本文以拉格朗日乘子法为理论基础，并考虑风电并网的经济调度方案。在GPU的操作平台上实现了并行算法。算法实现流程框图见图3。

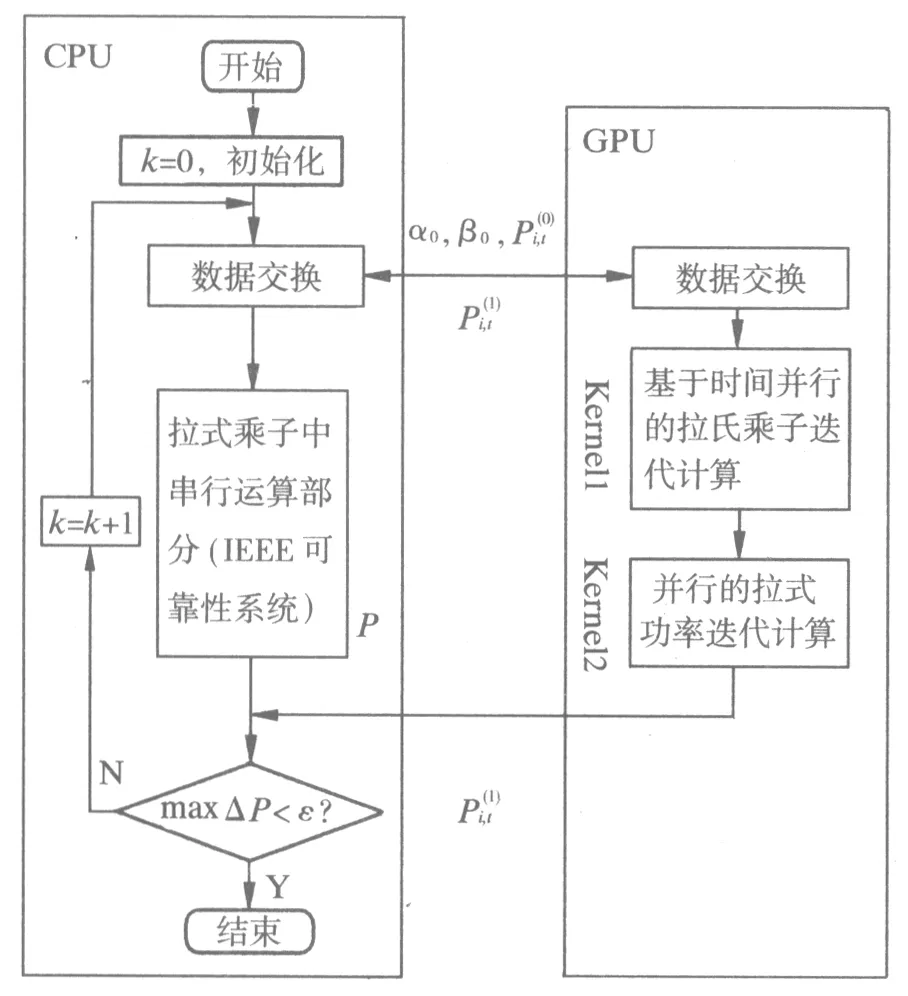
图3 算法实现流程框图

由图3得，一次变量迭代的计算步骤如下。

b. 以拉格朗日乘子法为整体框架，调整相应的并行算法公式，在CPU上处理数据输入接口和IEEE可靠性系统的串行部分。GPU通过流水线的形式处理具有相同表达公式的数据迭代部分，即功率变量迭代和乘子迭代, 其中功率变量迭代部分包括等式约束和不等式约束，其数量与机组的数量相关；

c. 当算法一轮迭代后，其功率变量的变化值不满足给定误差时，k=k+1进行下一轮迭代。先进行寄存器中数据的传导，传入新值给GPU中，迭代完后将又一轮新值重新传回CPU中，进行串行部分的数据可靠性检验和误差检验，直到满足为止。

3.2 算例验证

为了展示基于GPU的拉格朗日乘数算法的有效性和效率，IEEE可靠性系统分别在CPU上进行串行计算并在GPU和CPU上进行并行计算。CPU是英特尔核心i5 4690，计算机内存为16 GB，GPU为NIVIDIA 960，带有4 GB图形内存。

由于拉格朗日乘数优化已多年来成功应用于解决DED问题，因此证明了它的有效性和收敛性。 因此，只有基于GPU的异构和并行计算与传统的串行计算之间的差异才值得分析和讨论。

表1列出了GPU和CPU以及CPU在4种不同计算规模上所花费的时间。由表1可以看出，在计算规模较小的情况下，CPU上的串行计算速度比GPU和CPU上的异构计算速度快。只有当规模扩大到一定程度时，并行计算的优越性才能体现出来。

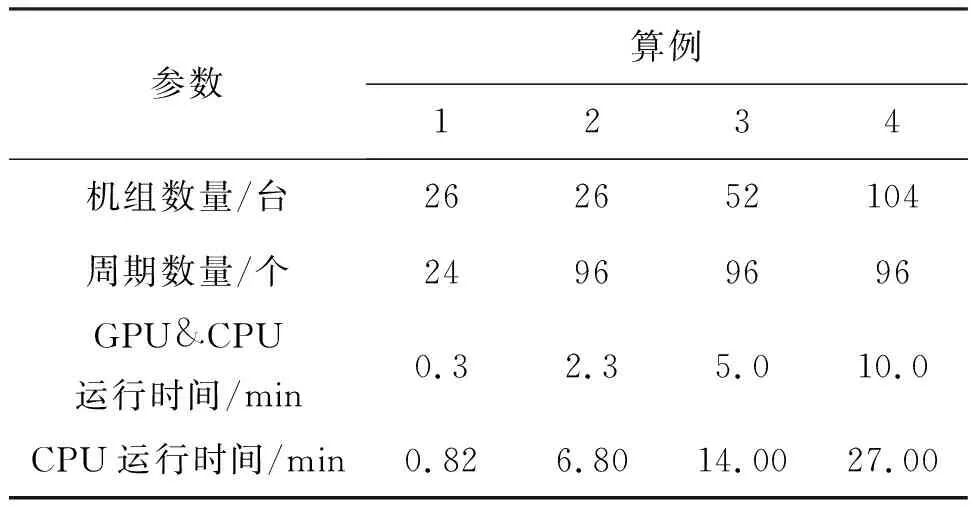
表1 并行与串行运算时间对比

从表1中还可以看出，在算例2中具有96个周期的CPU的时间是具有24个周期的算例1的7倍。 花费时间的增加趋势可以见图4。 曲线1是GPU和CPU上的异构并行计算，曲线2是CPU上的串行计算。可以看出，曲线2的增长速度快于曲线1。

图5中分别给出了3台机组在跌过程中，由全程CPU进行功率求解数值变化过程和由CPU&GPU协同进行功率求解数值变化过程，两类曲线在最后基本吻合。

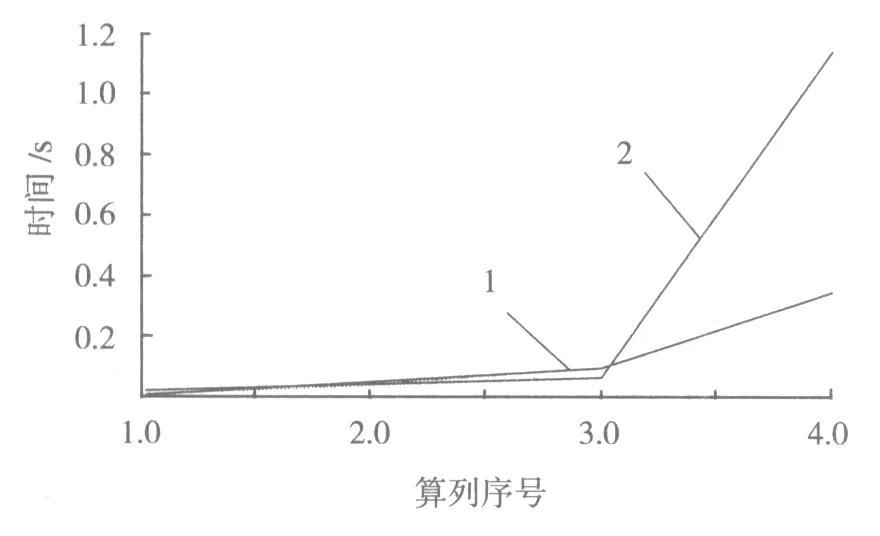
图4 并行与串行运算时间对比

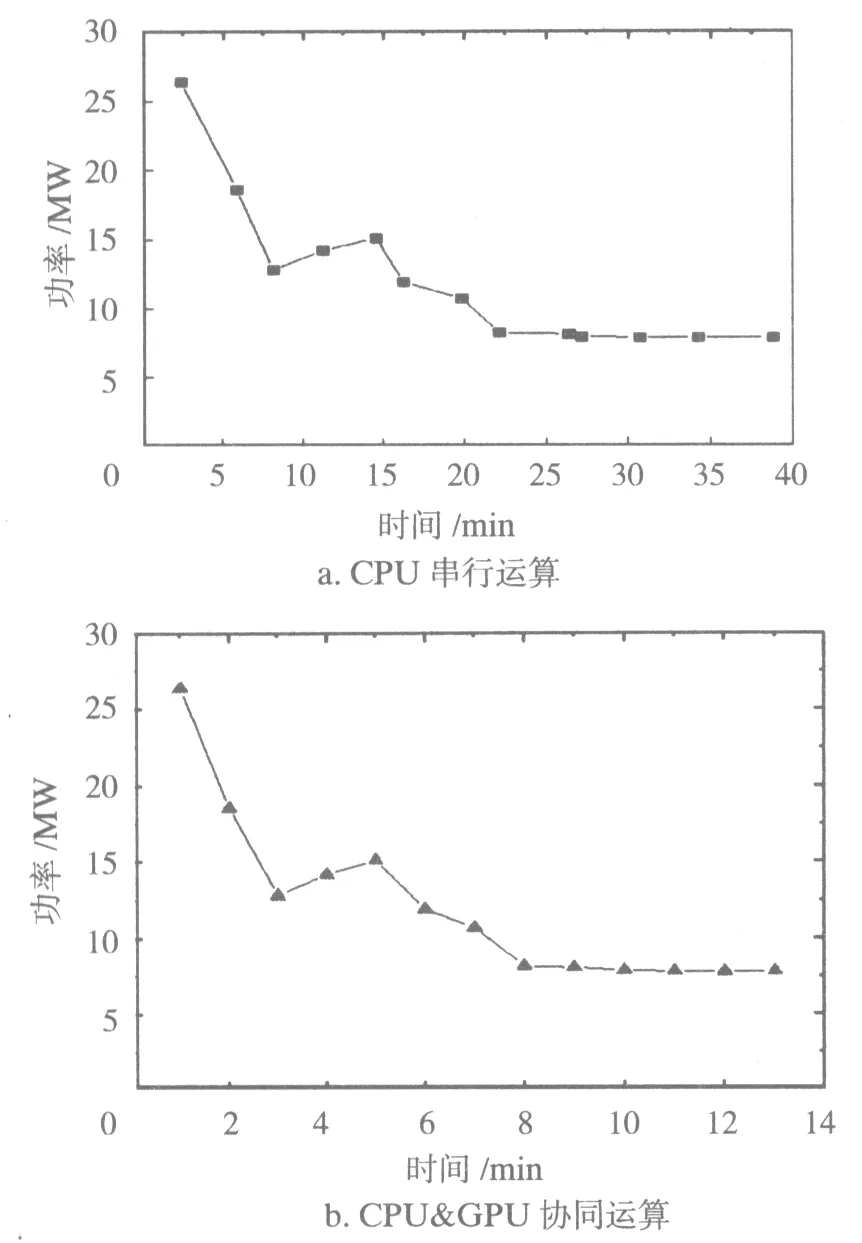
图5 全程CPU和CPU&GPU协同运算对比曲线

图5给出了4种算例的CPU与并行运算的时间对比，可以看出，GPU的并行协处理在运算规模越大的情况下，其优势明显会展现出来。

计算规模越大，异构计算可以节省更多时间。在大规模风电渗透增加DED复杂性情况，需要更多计算资源的情况下，基于GPU和CPU的异构计算在电力系统发电调度计算中起着重要作用。

4 结论

由于大规模集成和风电的高度不确定性，本文建立了一个新的模型，以减少不时出现的弃风， 并且基于GPU和CPU的异构并行计算拉格朗日乘子优化已被应用于求解所提出的模型。可以看出，在满足相同效果的前提下，基于GPU的并行具有更高的效率，并且适用于电力系统的优化计算。