基于近场零陷权的出砂监测干扰抑制方法

刘升虎，安 岑，党 博，王炳友，汪 伟

（西安石油大学，陕西西安 710065）

油气井在开采过程中[1，2]，有时候由于地质疏松、在流体的冲刷下，在油气管道传输时会夹杂着大量砂粒，随着时间的流逝，会导致管道腐蚀，更加严重的时候会导致管道破洞。但在出砂监测中，会受到来自现场的各种各样的干扰，尤其是来自于管道方向上的，为了获得准确的出砂监测信号，则需要对干扰进行抑制。波束成形[3]广泛应用于雷达的定位与目标识别和抗干扰等方面的研究,在远场模型下，利用阵列信号处理技术实现对目标的识别和干扰抑制。还有一部分应用于声呐、麦克风下的近场模型，比如[4-9]水下舰艇的识别和麦克风的声波聚焦成形来对声音进行识别并经过信号处理得到想要的声音类型[10]。有一类在对水中噪声源的识别过程中，对来波信号进行波束聚焦而对干扰方向形成零陷来达到抑制干扰的目的。远场下波的传播类型为平面波，而在近场模型下，声波的传播类型应按球面波来处理。在砂粒撞击管道过程中，会在管壁上产生振动信号，根据振动信号的传播类型，以及出砂监测的环境，在声波信号的分析中，声波向四周传播，类似于球面波，来对砂粒撞击产生的声波信号进行分析。通过构建出砂监测近场模型来实现对出砂信号的监测，在对干扰的抑制上，本文采用在信号的来波方向使输出功率最大化，在干扰方向在近场下形成零陷，来达到对干扰的抑制，通过对零陷最优权的计算，并对近场常规波束成形以及“零陷”下的波束成形进行仿真，结果表明，该方法能使信号输出功率最大的前提下，并在干扰的方向上形成零陷，能实现对干扰的抑制。

1 出砂监测模型的构建

油气井的出砂现象是比较常见的，砂粒会伴随着油气传输的过程中，在遇到弯管的时候对管壁造成冲击，产生振动信号，产生的超声信号被超声传感器所接收。所以，在进行出砂监测的时候，选择对产生的振动信号来进行分析。砂粒撞击管壁的情况以及阵列传感器的安装位置（见图1）。

图1 出砂监测模型

箭头所指方向为油气夹杂着砂粒的流动方向，传感器的安装位置为弯管下方2 倍管道直径处，图中黑点代表砂粒。

阵列传感器在接收砂粒撞击信号时，还会受到其他的干扰。主要干扰为管道振动所引起的，以及周围机器工作产生的噪声和管内液体流动的干扰，另外，周围环境也会存在着高斯白噪声。主要考虑油气井开采现场管道的内径大约为55 mm，外径为65 mm，考虑到传感器尺寸的大小及管壁的厚度，砂粒撞击管壁产生的超声高频信号，将会在1 μs～2 μs 被阵列传感器接收到，这将大大增加实时监测的困难性。同样，这也会影响到对于干扰信号的抑制。

根据出砂监测模型，砂粒撞击管壁产生的信号会透过管道被阵列传感器接收到，根据近场与远场模型划分的标准：

其中：λ-砂粒撞击管壁产生信号的中心频率所对应的波长；D-阵列传感器的孔径。

考虑到以上因素，本文选择构建近场模型，利用接收信号的延迟差，通过近场波束成形方法以及在干扰方向形成零陷达到对干扰的抑制。

常规波束成形技术一般是基于远场模型下来进行计算的，此时波的传播类型为平面波，时延差只与目标的方向有关，与距离无关，所以常规波束形成被称为空间方位滤波器。而近场下波的传播类型为球面波，不仅与方向有关，还和目标与阵列传感器的位置有关，根据目标点的不同分别需要进行距离差和时延差进行补偿。由于出砂现场环境的复杂性，传感器的安装位置以及管壁的厚度，阵列传感器接收到的信号将会有很强的相关性，给后续波束聚焦成形及在实现对干扰的抑制上带来极大的困难。假设阵列传感器由M 个参数一致的传感器组成，它们之间的间距都为d，假设声波的波长为λ，则间距一般设置λ/2，近场模型（见图2）。

图2 阵列传感器近场模型

均匀排列为一维线阵，信号和干扰源分别从不同的方向传播过来，假设信号源S1、S2…SP，它们的角度及方位分别为Si（θi，Ri），（θ2，R2）…（θp，Rp）。其中，Si（θi，Ri）为信号源到阵列的参考点（阵列中心也即是坐标零点）之间的连线与传感器阵列所在直线的夹角、和到参考点之间的距离，i 的取值范围为1：q。

由所建立的极坐标系可以得出，第i 个信号源Si到第m 个阵列的距离为:

式中：dm-第m 个传感器与参考阵元之间的距离，且：

由式（2）、式（3）可得第i 个信号源到第m 个传感器的距离与到参考点的距离之差：

由路程差则可以通过计算得到信号到达各传感器的时间差为：

这里取v=5 900 m/s。

2 基于近场零陷权的干扰抑制方法

通过上文对近场模型的构建以及出砂监测接收信号的复杂性和各个通道信号之间的相关性，为了实现对干扰的抑制，本文采用基于近场零陷权的干扰抑制方法来解决这个问题。

近场下得一维阵列传感器，M 个阵元接收到的信号为：

其中：X（t）=[X1（t），X2（t）…XM（t） ]为一维阵列接收到的信号；为波束成形权矢量，θ 为波束的指向角，每一个权矢量都是一个复数，它的模表示对幅度的加权，相位角表示信号的输出延迟。波束形成输出的平均功率为：

其中：X（t）=a（r，θ）S（t）+N（t），R 是接收信号的自相关矩阵。

近场模型，波的传波类型为球面波，时延性不仅与方位有关还与信号源到阵列传感器的距离有关，在极坐标系中，近场下的常规波束成形的权向量可以表示为：

其中：a（r，θ）=φe-jωτmi。

当波束扫描到信号点时，当r=Ri、θ=θi时，因为权系数对时延差和幅度的衰减进行了补偿，则会在信号源点处功率最大，形成“冒尖”现象，而干扰源也会产生这样的现象，为了达到对干扰的抑制，该文在干扰源形成零陷，在信号处使输出功率最大，而干扰处形成零陷。

考虑到砂粒撞击信号为窄带信号，最大功率可以表示为：

其中：max（P）-波束相对信号最大输出值；σ2-白噪声的方差，为一常数。假设干扰位置为（R1，θ1），约束条件为：

式（11）表示在干扰处形成零陷；由矩阵的广义逆求解可得：

其中：aH=A；ω-新的N 维向量；I-单位向量，求满足式（10）和式（12）条件的ω 即可获得满足全部条件方差的特解形式，于是，式（10）可简化为：

约束条件变为ωHAHAω=ωHAω=1。

最优权向量利用拉格朗日来构造函数求解，构造函数为：

将式（16）代入式（13），得到波束聚焦成形于零陷下的最优权向量：

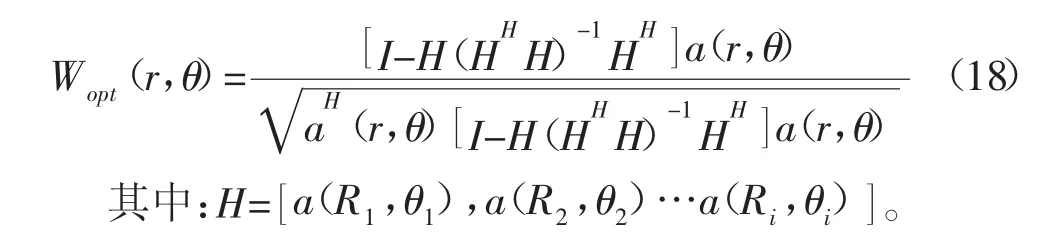
通过对零陷的最优权向量的推导计算，在近场模型下对信号的幅值和时延差进行补偿，在信号位置使输出功率达到最大，而在干扰处形成零陷来达到对干扰的抑制。

3 仿真分析

本文主要研究的管道振动所带来的干扰，在进行干扰抑制时，主要考虑沿着管壁的两个方向，结合传感器安装的位置，干扰方向为0°，180°。砂粒撞击管壁的方向主要为45°和60°方向，分别对上述情况进行仿真分析。相比于远场模型，近场模型不仅要考虑来波方向还要考虑焦距的长短，这里，设阵列传感器为等间距的一维线形阵列，焦点设置在阵列传感器的中心，假设阵元个数为5 个，阵元间距d=0.1 cm，阵元焦距为5 cm。信号的来波方向为45°，干扰方向为0°和180°。分别将常规波束成形与形成零陷的波束成形进行对比，比较两者的区别，判断对干扰的抑制效果。近场下的常规波束成形的仿真结果（见图3）。

图3 近场常规波束成形

常规波束成形只能大概确定接收信号的到来方向，而不能在干扰方向上形成一定的抑制。

下面在保持上述条件不变的前提下，通过将计算后形成零陷的最优权向量代入，得到形成零陷的近场波束聚焦成形（见图4）。

通过将两图进行比较，图4 在干扰方向上，也就是图中的0°和180°方向，较好的形成了“零陷”，达到了对干扰的抑制，并且在信号的来波方向上形成较大的功率输出。在不改变其他条件的情况下，信号方向为60°方向，得到的结果（见图5）。信号方向为60°时，在信号来波方向依然能良好的“冒尖”，并且在干扰处形成零陷，来达到对干扰的抑制。

图4 形成零陷的近场波束聚焦成形

图5 形成零陷的近场波束聚焦成形

仿真结果表明，此方法能够有效的抑制管道振动带来的干扰，也就是沿着管壁的两个方向0°和180°，并且能够使砂粒撞击方向输出信号功率达到最大，提高出砂监测的准确性。

4 结语

本文在通过出砂监测模型的构建，对砂粒撞击管壁所产生的振动信号进行简要的分析，并在近场模型的基础上，采用近场波束成形的方法，通过计算形成零陷的最优权向量，在干扰方向形成零陷来达到对干扰的抑制。在干扰源的角度已知的情况下，在来波方向输出功率最大的前提下，通过形成零陷来实现对干扰源的抑制，仿真结果表明，能较好的达到要求。在油气井出砂监测中，通过对干扰的抑制，来更好的体现出砂信号的真实性，更好的指导油气的开采，提高效率。