部分充填裂隙网络岩体的渗透特性分析

郑 双，张 斌，符文熹

(1. 四川大学水利水电学院，成都 610065；2. 四川大学水力学与山区河流保护国家重点实验室，成都 610065; 3. 四川省公路规划勘察设计研究院有限公司，成都 610041)

0 引 言

西南地区是我国水利能源开发的主要地区，目前已修建和在建大量的水利工程，大坝特别是高坝多位于基岩上，基岩的渗透性往往决定了整个坝基的渗漏[1]。然而，西南地区地质条件十分复杂，岩体在长期内外动力地质作用下，岩体内部常常发育大量的裂隙，形成裂隙网络岩体[2]。因此，研究裂隙岩体的渗透特性具有重大工程意义。

对于裂隙岩体，可采用裂隙网络方法进行渗流分析。Wittke[3]不考虑岩块的渗流，以真实的裂隙网络为基础，利用线单元法，创建了线素法，最早提出了岩体裂隙网络渗流模型。Wilson和Witherspoon[4]将有限单元法引入到线素法，计算了坝下理想裂隙网络岩体的渗流特性。王恩志[5]利用图论的思想对岩体裂隙网络进行了数学描述，给出了描述裂隙网络连通关系的数学方法，提出了一个新的地下水渗流数值模型。莫海鸿[6]基于拓扑学的理论，提出了裂隙网络的离散模型。赵红亮[7]通过计算机模拟构筑了三维裂隙网络系统。经过不断的发展，岩体裂隙网络渗流模型逐步走向成熟，得到了广泛的应用。

对于裂隙网络岩体的渗透特性，通常基于立方定理计算单裂隙的渗流量，通过裂隙组合进行分析[8]。Zimmerman[9]通过研究单相流在粗糙岩石裂隙中的运动，基于立方定理给出了Navier-Stokes方程的解，从理论上说明了立方定理的适用条件(雷诺数Re<<1)。柴军瑞[10]研究了裂隙水流为紊流且不满足立方定理条件下的裂隙渗透特性，给出了岩体裂隙网络非稳定渗流的控制方程。朱红光[11]在立方定理的基础上，推导了交叉裂隙的渗流计算公式，并将其应用到岩体裂隙网络分析中。刘日成[12]为了研究裂隙网络的非线性渗流，建立了两种离散裂隙网络模型，根据相应边界条件，对Navier-Stokes方程进行求解，并且通过室内透水试验进行了验证，提出粗糙的裂隙表面会导致渗流量降低，但是误差可以忽略不计。

综上所述，岩体裂隙的粗糙度、开度、交叉情况以及裂隙流的稳态和非稳态问题都得到了广泛细致的研究，然而，由于风化和侵蚀作用，天然岩体裂隙中常常存在一定厚度的充填物，此时直接采用立方定理进行计算，将产生较大误差。为了研究含充填介质裂隙网络岩体的渗透特性，本文建立了部分充填条件下的单裂隙渗透模型，结合Navier-Stokes方程和Brinkman-extended Darcy方程，得到了单裂隙流场分布特征，推求出单裂隙渗流量的解析解；在无充填的情况下，该渗流量表达式可以简化为经典的立方定理。后基于裂隙网络渗流原理，构建了含充填介质裂隙岩体渗流网络的数学模型，可以得到裂隙网络节点水头。结合案例分析，探讨了充填介质对裂隙网络岩体渗透特性的影响。

1 含充填介质裂隙渗透模型

1.1 理论模型

本文为了研究充填物对裂隙岩体渗透特性的影响，建立如图1所示的概化模型，裂隙宽度为e，填充物厚度为b1，空裂隙的厚度为b2，模型长度为L。假设裂隙中渗流流速为u，充填介质中渗流流速为w。模型存在下述的假设，①流体不可压缩，为层流；②渗流只沿着x轴的流动；③裂隙中渗流u符合Navier-Stokes方程[13]，充填物中的渗流w符合Brinkman-extended Darcy方程[14]；④充填物与裂隙渗流的交界面符合流速相等和剪应力连续的边界条件[15]。

图1 岩体裂隙的概化模型Fig.1 Generalized model of rock mass fracture

根据假设③，裂隙中流速u和充填介质中渗透流速w分别满足Navier-Stokes方程和Brinkman-extended Darcy方程，同时它们还满足连续性方程。

(1)

(2)

式中：p为流体压强，M/(L·T2)；ρ为水流密度，M/L3；n为孔隙率；η为水的动力黏度，M/(L·T)；K为充填介质的渗透率，L2；▽为Hamilton算子。

又由模型假设b，可得：

(3)

分别代入式(1)、(2)，可得

(4)

求解式(4)中的微分方程，可得：

(5)

(6)

式中：ΔP分别为裂隙两端的压强差。

根据假设，式(5)和(6)满足下述边界条件：

(2)裂隙渗流与岩石交界面处流速为0，即y=b1+b2时，ux= 0。

(3)充填物中渗流与岩石交界面处流速为0，即y= 0时，wx= 0。

联立上述边界条件即可求出参数B1、B2、C1、C2。

(7)

根据流速分布，可以求得整个裂隙断面的流量为：

(8)

可以发现当填充比(β=b1/b2)为0，即b1= 0时，式(8)可以化简得到：

(9)

式(9)即为经典的立方定理计算的裂隙流量。式(8)更具有普遍性，立方定理是它的一种特殊情况。

1.2 模拟试验

本文为了验证理论模型的正确性，开展物理模型试验进行验证。试验装置设计图如图2所示，整个模型长为30 cm，宽为20 cm，高为20 cm。其中的不透水岩块利用亚克力版制作的长方体模拟，长为20 cm，宽为20 cm，高为9.5 cm，可以达到不透水的效果，充填物采用河砂模拟，经过试验测定，渗透率K为3.54×10-8cm2，孔隙率n为0.39。为了防止填充物发生侵蚀破坏，采用铁丝网进行固定。根据设计进行组装，装填完的试验装置如图3所示。

图2 试验装置设计图Fig.2 Design drawing of test device

图3 试验装置Fig.3 Test device

参照土工试验方法标准进行渗透试验，分别在填充比为25%、50%、75%，在不同水头差ΔH条件下进行试验。将试验结果记录在表1中。表1中试验值均为多次试验的平均值。

将试验值与理论值进行对比，如图4所示。从图4中可以发现，理论值与试验值较接近，误差相对较小(小于10%)。在一定程度上可以验证本文提出含充填介质的岩体裂隙的渗流模型。

图4 试验值与理论值对比Fig.4 comparison between experimental and theoretical values

2 岩体裂隙网络模型

裂隙网络渗流模型首先由Wittke提出，后经过Louis、Wilson和王恩志等人的发展，现可以用于二维稳定和非稳定裂隙流的计算[16]。裂隙网络模型如图5所示，以岩体裂隙的交点为节点，两个节点之间的裂隙为一个线元。假设渗流域内有n个节点，与第i个节点相连的线元有m个，在节点i处，根据水流均衡原理[17]，可得节点i处的水流控制方程为：

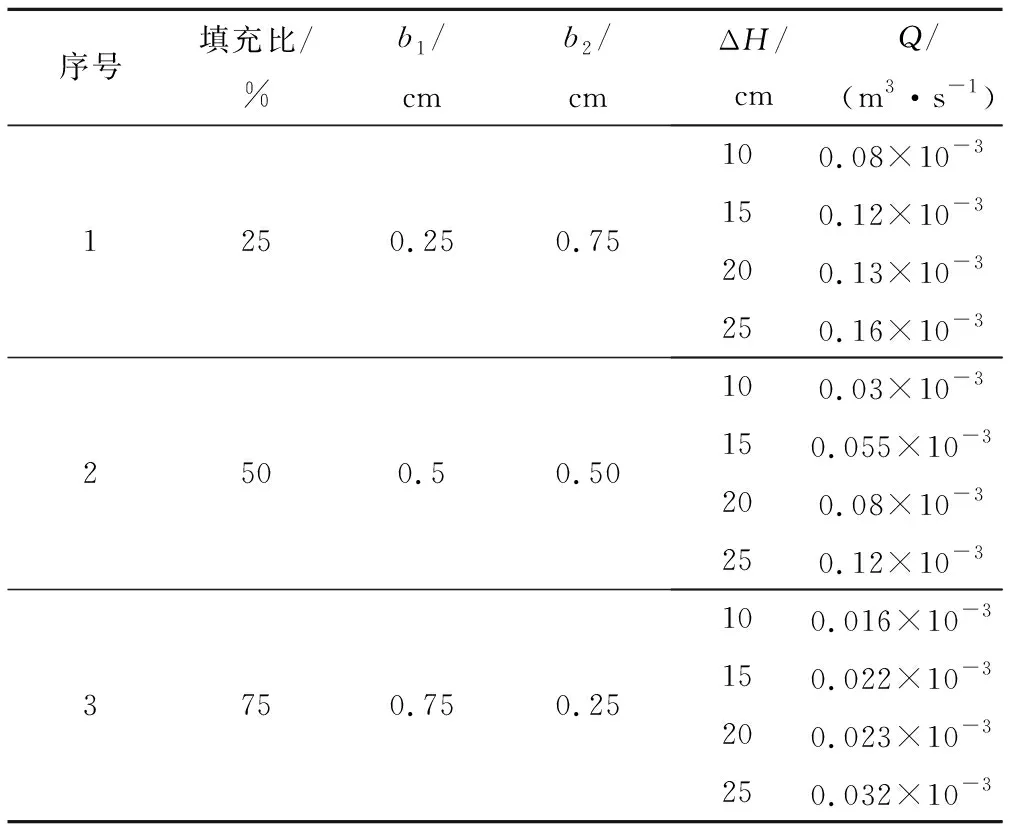
表1 试验记录表Tab.1 Test record table

图5 裂隙网络模型Fig.5 Fracture network model

(10)

式中：Qi为节点i的源项，i取值为：1，2，3,…,n。

若裂隙中存在充填物，则裂隙中的渗流量可按式(8)进行计算。将式(8)带入式(10)可得：

(11)

式中：bj-1为线元j中填充物的厚度；bj-2为线元j中空裂隙的厚度；wj-x为填充物中渗流的流速；uj-x为空裂隙中的渗流流速。

式(11)为裂隙中存在充填物条件下，节点i处的流量控制方程。由于整个渗流域内总共有n个节点，则整体的渗流控制方程为：

(12)

式中：A为裂隙网络的衔接矩阵，其为n×m阶矩阵。

它是用来描述渗流域中线元与节点的链接关系的矩阵，根据文献[5]可以求得。Q= {Q1,Q2, …，Qn}T。结合模型的边界条件，可以得到裂隙中存在填充物条件下，岩体裂隙网络渗流的数学模型为：

(13)

式中：Γ1和Γ2分别为已知水头边界；h1和h2分别为相应边界上的水头。

通过Matlab编程，求解式(13)，可以得到各个节点的水头。

3 算 例

如图6所示，大坝下的岩体中存在两组相互垂直的理想裂隙，岩块不透水，边界AC、BD、CD、EF分别为不透水边界。渗流沿着裂隙网络流动。边界AE的水头为100 m，边界BF的水头为20 m，AB长度为100 m，AC长度为40 m。裂隙的宽度为0.01 m，深度为0.1 m。水平向的裂隙含有厚度为0.005 m的充填介质，充填比β=50%，渗透率K=3.5×10-8m2。根据裂隙网络渗流原理，对节点进行编号，整个渗流域内共有51个节点，66个线元。

图6 模型与节点编号和节点详图Fig.6 Model node numbered and node detail

在裂隙分别为充填和不充填的条件下，根据本文的数学模型(含充填介质)进行计算，得到各节点的水头，如图7所示。根据节点编号，可以分为5个区间(1～9、10～20、21～31、32～42、43～51)，分别表示2条水平边界(AB、CD)和3条水平向裂隙上的节点水头。可以发现，在每个区间内，两种方式计算的水头变化趋势保持一致，都是逐渐减小，但是具有一定的差距，明显在裂隙含充填介质条件下，计算得到的水头变化幅度更大，具有更大的最大值和更小的最小值。

图7 各节点水头Fig.7 Water head of each node

图8为渗流域内的水头等值线图，可以发现，两种方式计算的结果具有明显的差别。在靠近渗流入口和溢出面的位置，裂隙含充填介质条件下，计算的水头等值线更加稀疏，水力比降较小，说明考虑充填介质会导致裂隙岩体的渗流量减小。另一方面，在渗流域的中部，含有充填介质裂隙岩体的等水头线较密，水力比降较大，渗流的流速增大，可能会导致局部的侵蚀破坏，影响裂隙岩体的强度。

在裂隙无充填的条件下，基于立方定理计算的渗流量为2.25 m3/s，在裂隙存在充填物的条件下，根据本文数学模型计算的渗流量为1.43 m3/s，相比下降了36.44%。可见，岩体裂隙填充物对裂隙岩体渗流特性的影响较大，不能忽略不计。

图8 渗流域内水头等值线图Fig.8 Isometric map of water head in seepage basin

为了研究充填介质的渗透率K对渗流量Q的影响，在不同填充比β的工况下，计算得到渗透率K与流域渗流量Q的关系，从图9中可以看出，随着渗透率下降，渗流量逐渐减小，当渗透率较大时，渗透率变化对流量的影响较大。当渗透率低于1×10-7cm2，渗流量随着渗透率的变化率将趋于0。填充度(β)越高，渗流量越小，当填充度为0时，计算的渗流量和文献基于立方定理计算的渗流量相等，这个也印证了式(9)的推导。

图9 不同填充度下渗透率与流量的关系Fig.9 Relationship between permeability and seepage volume with different filling degree

含填充介质裂隙岩体的渗透特性不仅与填充介质的渗透系数有关，还和裂隙的填充比β有关，在实际的工程中，它可以通过野外调查获得。为了研究填充比对含充填介质裂隙岩体渗透特性的影响，在充填介质具有不同渗透率的情况下，计算填充比与渗流量的关系，获得图10中的曲线，发现渗流量与填充比具有非线性的关系，曲线具有两个拐点。当填充比较小，低于30%时，曲线斜率较小，渗流量随填充比的变化率较小。当填充比较高，位于30%到70%之间时，曲线斜率较陡，渗透量随填充比的变化率较大。当填充比高于70%，曲线再次变缓，渗透量随填充比的变化率再次减小。

从不同渗透系数的关系曲线上看，填充比越高，充填介质渗透系数对渗流量的影响也越大，这是由于当填充比较低时(β<50%)，岩体裂隙的渗透量主要由空裂隙中的渗流量控制，渗流量受填充介质的影响较小；当填充比较高时(β>50%)，岩体裂隙的渗透量主要由填充介质中的渗流量控制，渗流量受填充介质的影响较大。

图10 不同渗透率下填充比与流量的关系Fig.10 relationship between filling ratio and seepage volume under different permeability

4 结 论

通过对部分充填条件下的单裂隙渗透模型的理论分析，推导出了含充填介质的岩体裂隙的流速分布，获得了单裂隙的流量公式。当填充度为0时，该渗流量公式可以化简到立方定理，室内渗流试验的结果验证了理论分析的正确性。后结合裂隙网络的渗流原理，建立了含充填介质的裂隙网络的数学模型，可以求解裂隙岩体的渗流场。

在算例中，以填充比和填充介质的渗透 系数为指标，讨论了填充介质性质对裂隙岩体渗透性质的影响。充填介质渗透率越小、填充比越高，裂隙岩体的渗流量越低。充填介质的存在会还导致裂隙两端的水力比降增加，提高裂隙的渗流流速，增加局部发生冲刷侵蚀破坏的可能性，进而影响裂隙岩体的整体强度。