基于模糊PID 控制策略的精密光学斩波器改进与仿真
翟保尊
(黄河水利职业技术学院,河南 开封 475004)
0 引言
精密光学斩波器用于对微弱光信号的检测,其工作原理是,通过直流电机带动斩波轮旋转,将光源发出的光辐射信号调制成交变光信号, 并通过光电转换,得到一定频率的电压信号,该信号与斩波器输出的参考频率信号一起被输入到后续的锁相放大器中,实现对微弱光谱信号的相关检测[1]。 锁相放大器采用互相关的检测原理,测量与参考信号同频率信号的幅度。 因此,将微弱光信号调制成与参考信号相同频率至关重要。如果待测信号频率和参考信号频率存在一定量值的偏差,就会对测量结果造成严重影响。因此,光学斩波轮的转速控制精度及稳定度至关重要[1]。
现有的光学斩波器主要采用传统的PID 控制方法, 被控对象必须具有准确的数学模型才能达到较好的控制效果。而在实际工程中,被控对象不可能是一个理想模型,因而难以有具体准确的数学模型,这就导致传统PID 在精密光学斩波器上的控制效果有限[2]。鉴于此,笔者将模糊控制和PID 控制结合起来,对精密光学斩波器控制算法进行改进,使其既具有模糊控制适应性强、 快速性好的优点, 又具备PID 控制稳态精度高的特点。
1 精密光学斩波器控制系统的数学模型
1.1 精密光学斩波器控制系统的组成
精密光学斩波器控制系统主要由STM32 微控制器、L298N 功率驱动电路、斩波装置以及光耦测速反馈装置组成,如图1 所示。该系统通过将转速设定模块设定的转速与实际测得的转速进行比较, 将偏差传递给STM32 控制器进行处理, 输出PWM 方波,经驱动电路后,对斩波装置中的直流电机进行速度调节[3]。
1.2 主控电机等效模型
PWM 调节的实质是通过对电机两端电压的调节,控制电机的转速。 在控制系统中,主控电机的等效电路模型如图2 所示。
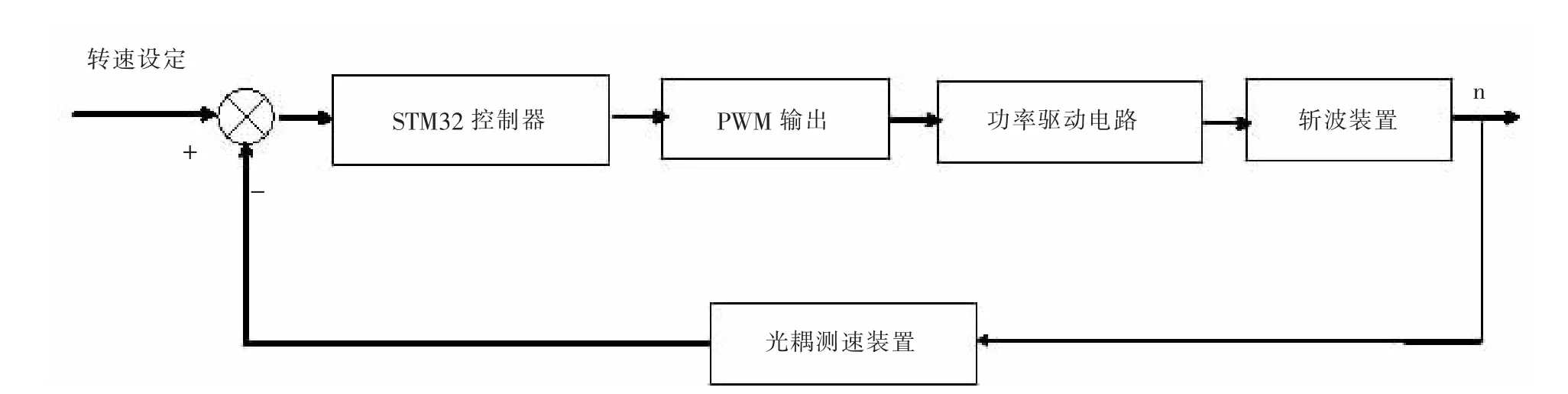
图1 精密光学斩波器控制系统结构图Fig.1 Control system structure of precision optical chopper

图2 直流电机等效电路模型Fig.2 Equivalent circuit model of DC motor
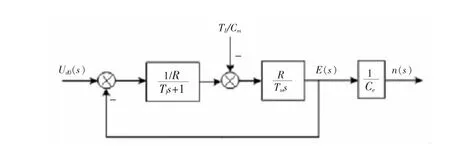
图3 主控电机拉氏变换后动态结构图Fig.3 Dynamic structure after Laplace transform of master motor
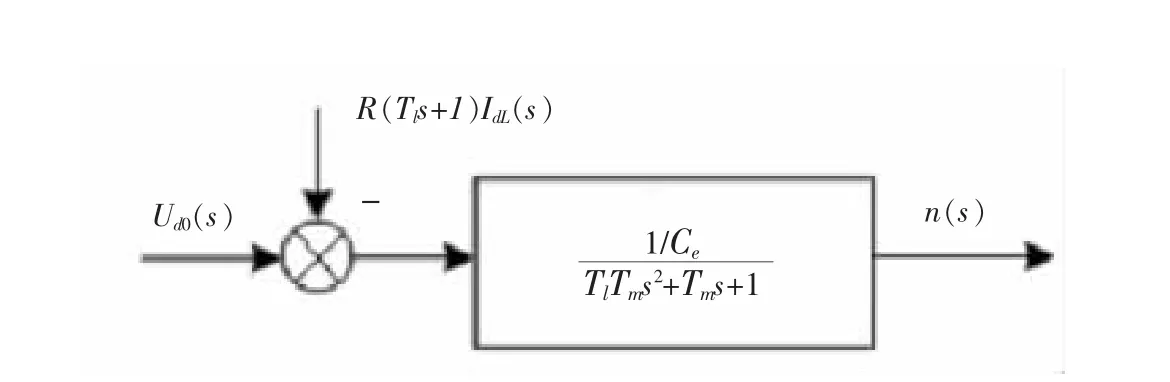
图4 简化动态结构图Fig.4 Simplified dynamic structure

图5 负载电流为零时动态结构图Fig.5 Dynamic structure of zero load current
2 模糊PID 控制算法研究与仿真
2.1 原理分析
市售光学斩波器的控制器程序通常采用可靠性较高、技术较为成熟的PID 算法。PID 算法主要用于被控对象参数稳定、非线性不很严重的系统。而光学斩波器中的主控电机是一个典型的非线性系统,由于干扰因素的突然扰动、 温度变化以及器件用久的磨损, 要想获得满意的控制效果, 就要对PID 的3个控制参数进行不断调整。 而模糊控制器不需要被控对象精确的数学模型,只需根据PID 参数整定的工程经验,制定模糊规则,确定控制决策。因此,将模糊控制器和PID 控制器进行结合, 将是一种实用、简便、可行的方案[4]。
模糊PID 控制器是把输入PID 调节器的偏差及偏差变化率同时输入到模糊控制器中, 经过模糊化、 近似推理和反模糊化处理后, 得出调节因子△KP、△KI、△KD, 从而实现对PID 调节器中3 个参数实时更新和调整,其基本原理如图6 所示[5]。

图6 模糊PID 原理图Fig.6 Fuzzy PID principle
2.2 模糊控制器的构建
打开MATLAB 模糊工具箱,选择二阶控制结构,设置为两输入三输出类型,如图7 所示。其中,模糊控制器的输入为误差e 和误差变化率ec,输出量为参数调整量△KP、△KI、△KD,对应的模糊子集表述为:{负大,负中,负小,零,正小,正中,正大},也即{NB,NM,NS,Z,PS,PM,PB}, 量化论域均设为 {-3,-2,-1,0,1,2,3}。 e 和ec的基本论域取[-10,10],量化因子为0.3。 △KP的基本论域取[-15,15],量化因子为5。△KI的基本论域为[-3,3],量化因子为1。 △KD的基本论域为[-0.6,0.6],量化因子为0.2。 在隶属度函数编辑器中,选择输入、输出量的隶属度函数均为三角形(trimf),输入偏差e 的隶属度函数如图8 所示。

图7 MATLAB 模糊工具箱Fig.7 MATLAB fuzzy toolbox

图8 变量e 的隶属度函数Fig.8 Membership function of variable e
为使控制系统的性能达到最佳状态, 结合精密光学斩波器参数整定的工程经验, 制订如表1 所示的模糊规则[6]。根据表1,在MATLAB 模糊控制器中建立49 条模糊规则。
2.3 Simulink 仿真
将斩波器电机参数(Tl=0.000 043 s、Tm=0.039 s、ce=0.8)代入图5 结构图公式,可大致计算出系统理想状态下的传递函数,如式(9)所示。

在MATLAB 软件中,打开SIMULINK,建立模糊PID 控制仿真模型,如图9 所示。 在Fuzzy Logic Controller 模块中, 导入Chopper_fuzzPID.fis 文件。PID 控制器的控制参数初始值取为:KP=150,KI=79,KD=1.3。 模糊控制器根据偏差e 和偏差的变化率ec,输出修正值△KP、△KI、△KD给PID 控制器的3 个参数,实现PID 参数的实时调整[7-8]。
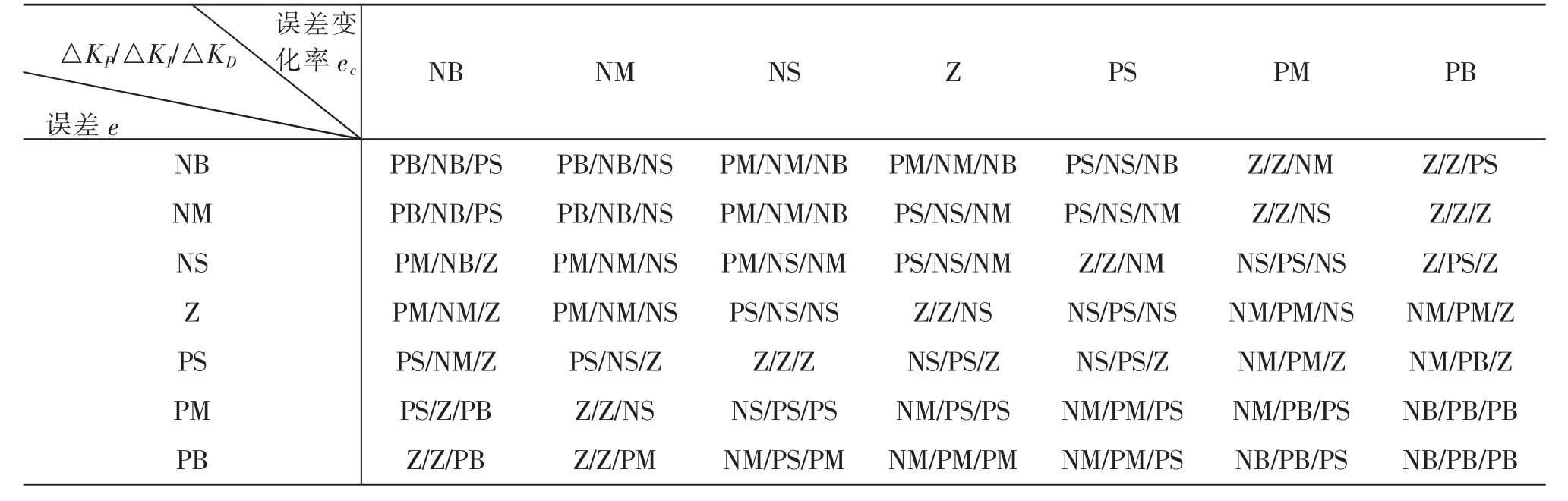
表1 模糊PID 控制规则表Tab.1 Rules of fuzzy PID control

图9 模糊PID 控制仿真模型Fig.9 Simulation model of fuzzy PID control
2.4 仿真结果分析
对系统而言,单位阶跃信号是比较苛刻的。如果系统对单位阶跃信号的响应较好, 则对其他信号的响应也会比较满意。 图10 为采用模糊PID 控制策略后,对系统施加单位阶跃信号的仿真曲线。从图10中可以看出,响应信号能够平稳快速、无超调地实现无差跟踪,控制效果令人满意。 图11 为同等条件下仅采用传统PID 控制的仿真结果。 从图11 中可以看出,系统响应时间较长,且会产生超调。由此可见,精密光学斩波器调速系统采用模糊PID 的控制策略后,可以有效避免传统PID 控制方法容易出现的超调和轻微震荡,调速的稳定性和快速性更佳。

图10 模糊PID 控制仿真结果Fig.10 Simulation results of fuzzy PID control
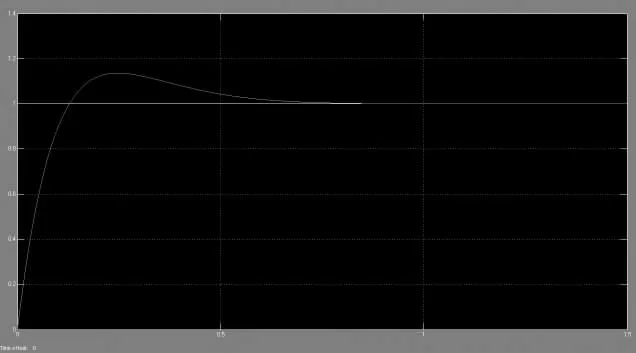
图11 传统PID 控制仿真结果Fig.11 Simulation results of traditional PID control
3 结语
综上所述, 以精密光学斩波器的控制系统为研究对象,从市面上现有斩波控制器所采用的PID 控制算法入手, 分析了其优缺点和局限性。 在此基础上,采用模糊PID 控制策略对精密斩波器控制系统进行改进, 并通过MATLAB 软件进行了仿真。Simulink 仿真结果表明, 采用模糊PID 控制策略改进后的精密光学斩波器较传统光学斩波器的调速稳定性和快速性更好。

