基于SVM 法的大坝安全稳定预测模型分析及应用

徐海峰，朱 晶，王艳波

（南京市水利规划设计院股份有限公司，江苏 南京210022）

0 引言

大坝失事不但工程毁坏， 而且会对下游地区的经济建设和人民生命财产造成毁灭性灾害。 国内外不同程度的溃坝教训使人们对大坝的安全隐患越来越重视， 从而使大坝安全管理中的安全监测及预测也愈显重要［1-2］。 在大坝变形预测方面，国内外学者采用的模型主要有统计模型和BP 神经网络预测模型［3-4］。这些模型的预测精度均需依托于大量的统计数据， 而样本因素的选择对所建模型的预测精度影响较大，并易陷入局部极值。近几年发展起来的支持向量机算法（Support Vector Machine，简称SVM）能科学有效地规避以上问题。支持向量机算法是一种基于统计学理论的机器学习新方法［5］。 它是20 世纪70年代末AT＆Bell 实验室的Vapnik 等根据统计学习理论中的结构风险最小化提出的一种针对小样本训练和分类的机器学习理论， 其重要参数有松弛系数、惩罚因子及核函数［6-7］。 前两个参数是用来处理样本数据的误差问题， 通常采用大量对比实验的方法取定。核函数则是将高维非线性问题降为低维问题的参数。笔者试以白羊山水库工程为例，通过分析坝型及布置条件，确定大坝安全稳定预测模型的样本因素，以大坝安全系数为预测目标，建立SVM 大坝安全稳定预测模型， 并采用遗传算法对模型的重要参数进行优化分析， 以期为大坝安全监控提供一种新的解决思路。

1 工程概况

1.1 工程标准等级

白羊山水库工程库区地形呈“M”形，地势总体起伏不大，东、北、西三面地势相对较高，地面标高为17.00～22.00 m，南部靠龙河，地势较低，地面标高为5.00～10.00 m。 依据《防洪标准》（GB50201-2014）和《水利水电工程等级划分及洪水标准》（SL252-2000），白羊山水库属小（1）型水库，工程等别为IV等，其主要建筑物大坝、溢洪道的级别均为4 级，次要、临时建筑物级别为5 级。大坝的设计洪水标准采用30～50 年一遇， 校核洪水标准采用300～1 000 年一遇。白羊山水库下游为仪征市，其设计洪水标准采用30 年一遇，校核洪水标准采用300 年一遇。 根据《中国地震动参数区划图》（GB 18306-2015）， 区域地震动峰值加速度为0.15 g， 相应场地地震基本烈度为VII 度。

1.2 坝型选择

根据坝址地形条件， 白羊山水库工程可选坝型主要有土石坝和砌石重力坝两种。 不同坝型对坝基岩土体的要求不一样， 白羊山水库工程坝址处岩土体以粉质黏土为主， 难以满足重力坝对承载力及变形的要求， 宜选择对建基面岩土体要求相对较低的坝型，如心墙坝、斜墙坝、均质土坝和混凝土面板堆石坝等［8］。各种坝型比选统计情况如表1 所示。经综合比选，该工程选用碾压式均质土坝。

1.3 工程布置

白羊山水库工程大坝布置于两个高地之间，坝长1 800 m，最大坝高8 m。 大坝中部有一块高岗地将库区一分为二（宣家湾一级站和裴庄二级站分别位于这两片区域）。 为将两片水域连通，坝轴线选择东西向折线布置，大坝中部选择开沟连通，尽量避开高岗地。溢洪道布置在大坝右侧一垭口处，距离右侧坝肩470 m。 溢洪道由进口段、控制段、泄槽段、消力池和海漫段组成。放水涵洞布置在大坝左侧，距离左侧坝肩570 m。 补水涵洞位于原宣家湾一级站出水渠处，距离右侧坝肩197 m。 大坝具体布置如图1 所示。

表1 坝型比选统计表Tab.1 Statistics of dam type comparison

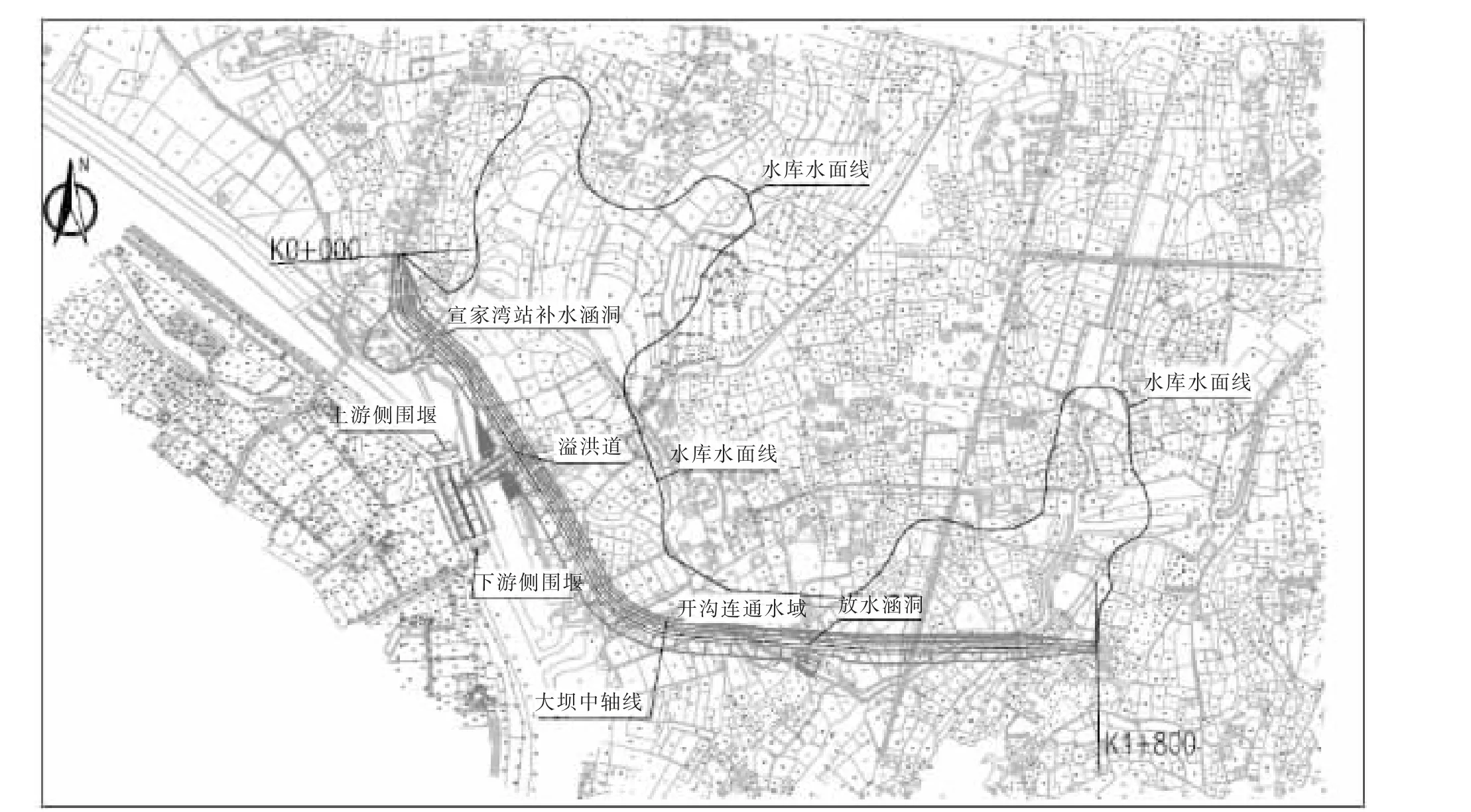
图1 大坝总体布置示意图Fig.1 Schematic diagram of dam overall layout

2 SVM 预测模型

2.1 计算断面及工况

依据测量资料和钻探断面，并综合考虑地形、地质及坝高等因素， 选取大坝K0＋280、K0＋780、K1＋080、K1＋380、K1＋580 断面作为计算断面，其中，K0＋780 断面为水库最大坝高断面， 其地质勘查剖面如图2 所示。限于篇幅，本文仅列举较为危险的水位降落期工况进行分析。

2.2 计算参数

渗透系数取地质勘查结果的平均值， 水位降落期采用总应力法确定， 土的抗剪强度应采用固快指标，大坝土层渗透系数见表2。

2.3 预测模型样本

上游坝坡水位降落范围为16.04～15.00 m，下游水位为9.50 m。采用Autobank 计算软件进行分析计算，得到5 个样本数据，如表3 所示。

3 参数优化及预测模型应用

3.1 松弛系数及惩罚因子优化

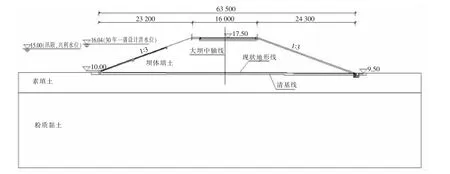
图2 大坝典型断面示意图（K0＋780）Fig.2 Schematic diagram of dam typical section （K0＋780）

表2 大坝渗流及稳定计算参数表Tab.2 Dam seepage and stability calculation parameters

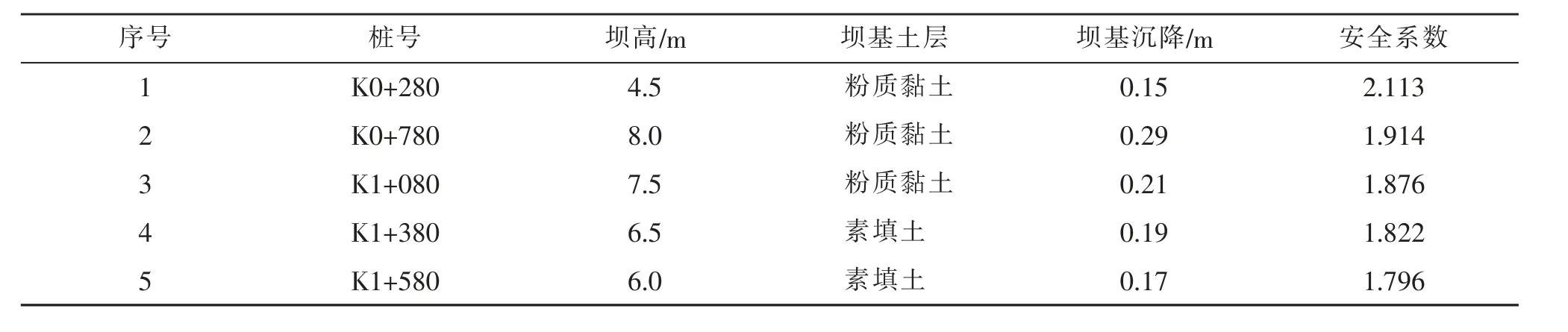
表3 大坝稳定预测模型样本数据统计表Tab.3 Statistics of sample data of dam stability prediction model

松弛系数ξ 和惩罚因子C 是用来解决样本数据误差问题的参数。本文采用遗传算法，搜索其最优参数， 并将搜索过程中出现过的所有参数变量与相应预测精度值都记录下来，绘成直观的等高线图（如图3 所示）和三维视图（如图4 所示）。 经分析，得到根据表3 中样本集所建SVM 预测模型的最佳惩罚因子C 为0.108 8，最佳松弛系数ξ 为0.574 3。

3.2 核函数比选

在SVM 方法中，核函数可以看作是样本之间定义的一种距离，它的选取会影响SVM 模型的拟合性能和预测性能。 这一特点为解决算法中的维数灾难问题提供了一个有效途径。 核函数的基本作用就是通过转换低维空间里的向量， 计算出在高维空间里经过相应变换的向量内积值。在回归分析中，多项式核函数为全局核函数，其处理外插值能力较好，但函数拟合能力较差（其处理内插值能力较差）。 径向基核函数是局域核函数，处理内插值能力较好，但处理外插值能力较差。 由于各样本集中的样本数量级接近，本次预测模型采用多项式核函数。

3.3 预测模型的建立及检验

利用表3 中的5 组样本集建立大坝安全稳定预测模型， 之后随机选取大坝沿线另外3 个断面的数据作为检验样本，对预测值与计算值进行比较，结果如表4 所示。 由表4 可知，利用本次所建SVM 预测模型可以较好地进行大坝安全稳定预测， 其预测误差绝对值最大仅为0.004。

图3 SVM 模型参数寻优等高线图Fig.3 Optimal contour of SVM model parameters

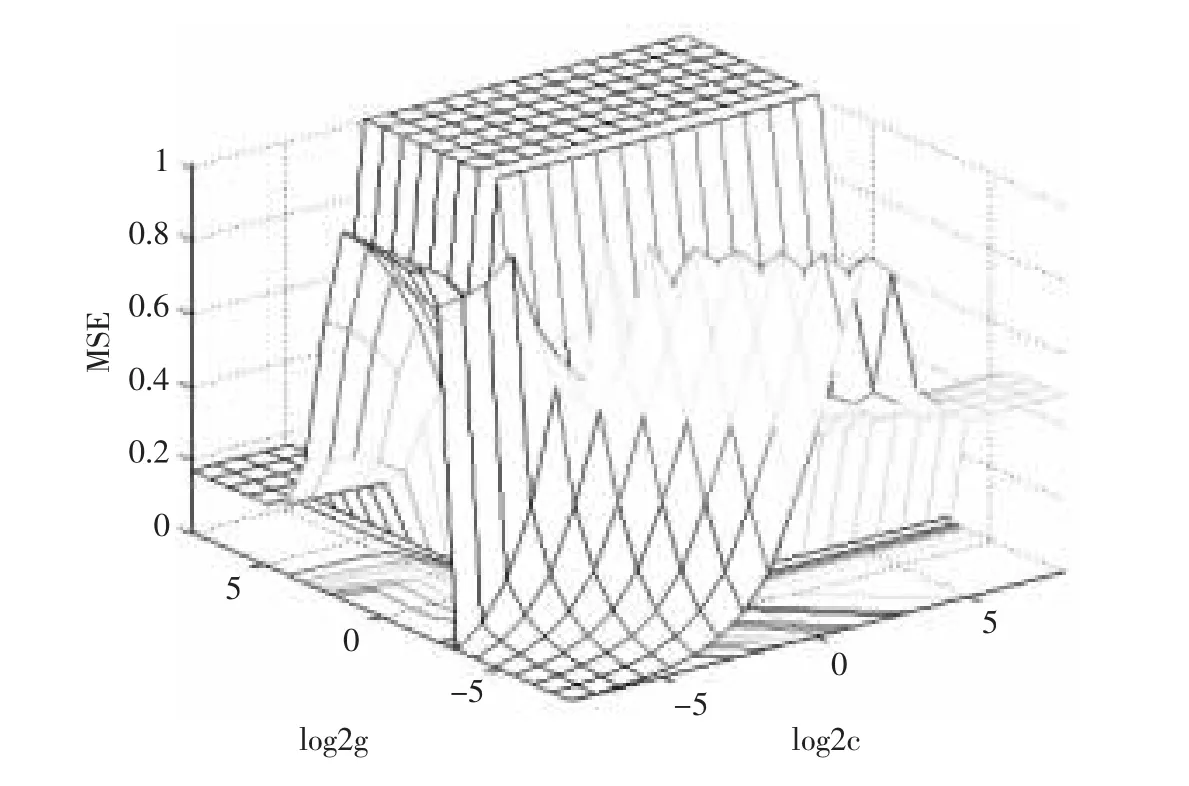
图4 SVM 预测模型参数寻优3D 视图Fig.4 Optimal 3D view of SVM prediction model parameters

表4 大坝稳定预测模型检验样本数据对比表Tab.4 Comparison of test sample data of dam stability prediction model

4 结语

本文应用遗传算法对模型参数松弛系数ξ 和惩罚因子C 进行快速优化搜索，根据样本因素非线性且数量级相近特点，选用的多项式核函数，采用5 组样本集建立了SVM 大坝安全稳定预测模型，并用该模型对大坝进行安全稳定预测， 预测结果的最大绝对误差仅为0.004，最大相对误差仅为0.24%，预测精度能够满足设计要求。该结论证明了SVM 预测模型具有小样本、非线性特点，也为提高大坝安全监控精度提供了新方法、新思路。