基于GM(1,1)模型的绕阳河流域丰水年预测
王 垠
(辽宁省阜新水文局,辽宁 阜新 123000)
1982 年我国控制论专家邓聚龙教授提出了灰色系统理论,该理论一经提出后便在国际上引起了极大的关注。其主要观点是把随机量看作在一定范围内变化的灰色量,尽管这些灰色量间存在着无规则的干扰因子,但经过处理后总能发现其规律性。它是一种独特的预测方法,一般表达方式为GM(1,1),即表示利用n 阶微分方程对x 个变量所建立的模型,在原始数据量较少时具有优势。目前,灰色理论已经广泛地应用于农业科学、经济管理、水利水电、生命科学等各学科,灰色预测是灰色系统应用的范畴之一。灰色预测是通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据数列,然后建立微分方程模型,从而预测事务未来发展趋势的状况。常见的灰色模型有GM(1,1)、GM(2,1)、DGM 和Verhulst,其中后三者适用于非单调的摆动序列或有饱和的S型序列,而GM(1,1)模型适用于具有较强指数规律的序列,因此,在灰色预测中,GM(1,1)灰色模型是最常用的模型[1]。目前,GM(1,1)模型广泛应用于水文数据预测方面的研究中,如杜小刚、原文林等人应用改进GM(1,1)模型对某站的径流量做出中长期预测[2];李东奎、冮行久应用灰色模型对柳河流域的干旱年进行模型建立及预测[3];李建峰,吴爱祥等人利用GM(1,1)模型对某边坡工程降雨量进行模型建立及预测[4]。
1 灰色系统的GM(1,1)预报模型
GM(1,1)主要形式是将离散的随机数经过依次累加成算子,削弱其随机性,得到较有规律的生成数,然后建立微分方程,解方程进而建立模型。其模型建立具体方法如下:
将X(0)设定为原始时间序列,则X(0)可生成序列X(0)=X(0)(k)(k=1,2,3……n),设X(1)为生成序列,则X(1)=X(1)(k)(k=1,2,3……n)。根据GM(1,1)模型概念将离散的随机数经过依次累加成算子,当增加滤掉信息时,X(0)和X(1)之间关系为由于上式为随机数据的累加形式满足指数分布,故可得关于X(1)的微分方程。本文将X(1)看为关于时刻t 的连续函数,X(1)=X(1)(t),建立GM(1,1)模型:

式中:α 和μ 为模型参数。
由(1)式可得X(1)的离散的预测数列:
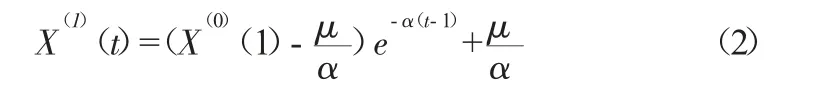
通过数列计算确定α 和μ 值后,按模型进行递推即可求得预测的累加数列,通过检测后,再进行累减,即可得到预测值。本文均为等时间,间隔Δt=1,因此,ΔX(1)(t)=μ+αX(1)(t),前差Δf 和后差Δb 分别为:

由(5)按最小二乘法原则可以求出(2)式的系数矩阵:
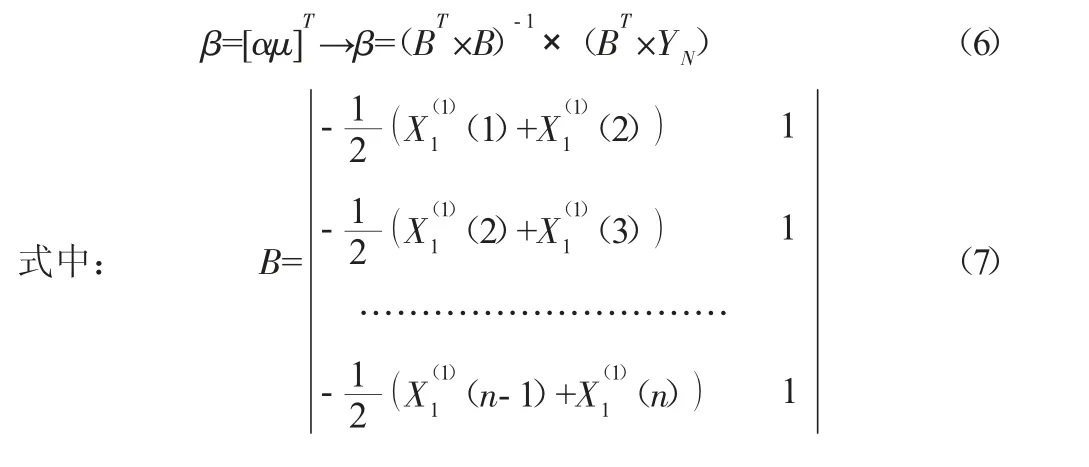

2 GM(1,1)模型的应用
2.1 绕阳河流域丰水年预测模型建立
绕阳河发源于辽宁省阜新市阜蒙县扎兰营子乡骆驼山,境内河长114 km,境内流域面积3669.1 km2,流域形状呈扇形。其主要支流有羊肠河、东沙河、二道河、苇塘河等。本流域地势多属丘陵,西高东低,植被稀疏,水土流失严重。该流域降雨时空分布不均,属暴涨暴落河流,多年平均降雨量为439.8 mm,多年平均蒸发量为1746 mm。该区域四季分明,雨热同季,日照丰富,干燥多风,因自然地理条件不同,气候差异显著。流域内有韩家杖子水文站,位于绕阳河上游,该断面以上流域内包括阜蒙县的鹜欢池镇、建设镇、塔营子乡、平安地镇,彰武县的哈尔套镇和四堡子镇部分地区。本文采用流域内韩家杖子水文站1951 年~2018 年降雨资料,利用GM(1,1)模型对本流域的丰水年进行预测。韩家杖子水文站历年降雨量见图1。
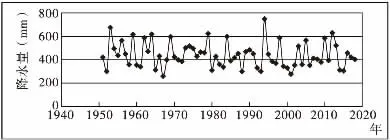
图1 韩家杖子站历年降水量过程线图
根据韩家杖子水文站降雨资料,本文以大于600 mm 的年份作为丰水年,建立表1。其中X(0)为洪水年份在时间序列中的排列位数,X(1)为其排列位数累加项。

表1 丰水年对象表
按式(7)、式(8)得:

2.2 模型精度检验
2.2.1 后验差检验
后验差检验,即对残差分布的统计特性进行检验。后验差检验是按照精度检验C(后验差)和P(小误差概率)两个指标进行检验。

其中e(0)(t)=x(0)(t)-x(0)(t),t=1,2,…,n 为残差数列。
3)计算后验差比值
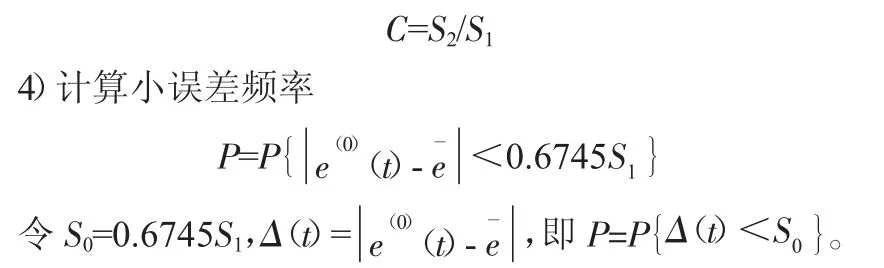
后验差检验要求指标C 越小越好,C 指标越小表示S1越大而S2越小;指标P 越大表明残差与残差平均值之差小于给定值0.6745S1的点越多。其精度等级可以根据表2 判断。

表2 GM(1,1)模型精度表

所有的Δ(t)均小于0.6745S1,因此可以判断,P=1>0.95,C=0.12<0.35,模型精度为好,计算模型合格。残差具体计算过程见表3。
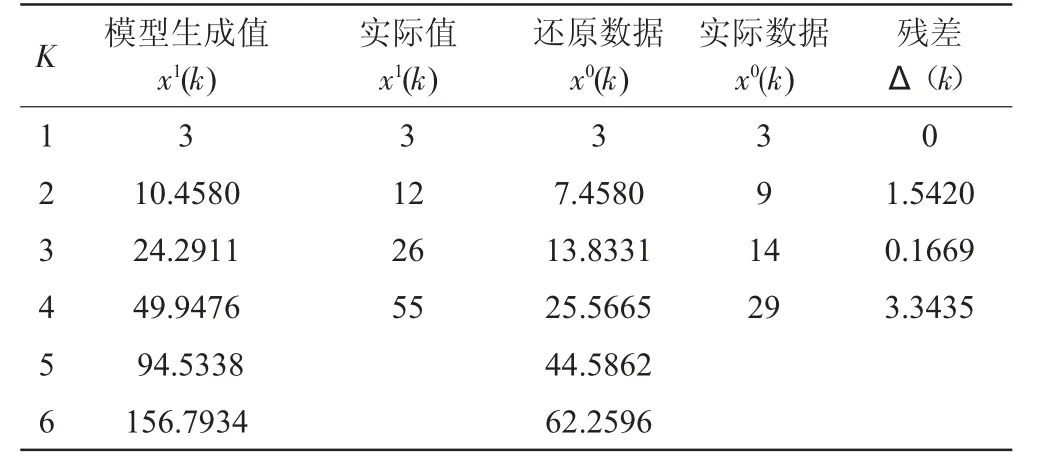
表3 残差检验表
2.2.2 关联度检验
关联度即是在预测值与累加值(或还原值与原始值)之间,计算其接近程度。关联度大,精度较高,反之则差。对GM(1,1)模型做关联度检验,可以以x0(k)作为参考系列,与x1(k)作关联度分析。关联系数计算利用如下公式:
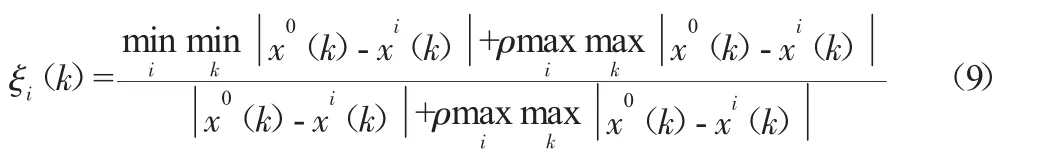
其中X0(k)为参考数列的第k 个取值,Xi(k)为比较数列第k 个取值,ρ∈[0,1]为分辨系数,一般取ρ=0.5。
根据表3 残差检验表,由于i=1,所以:
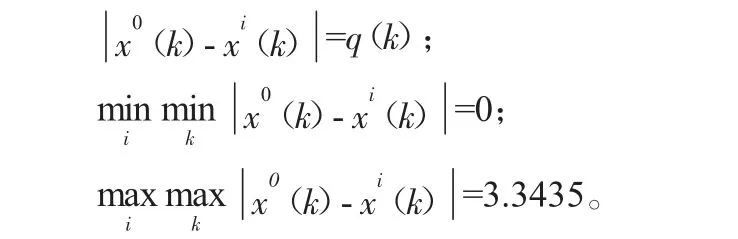
因此根据公式(9):ξ(1)=1;ξ(2)=0.5201;ξ(3)=0.9092;ξ(4)=0.3333。

3 绕阳河流域丰水年预测
根据模型计算,当k=5 时,x1(5)=94.5338,还原数据x0(5)=44.5862;还原数据减去原点年份数据,则第五次洪水发生年份为第四次丰水年份后的第15 年,即1994 年。根据韩家杖子雨量站历年降雨量数据,1994 年雨量为751 mm,降雨量大于600 mm,符合实际情况。
当k=6 时,x1(6)=156.7934,还原数据x0(6)=62.2596;还原数据减去原点年份数据,即预测第六次丰水发生年份为第4 次丰水年份后的第33 年,即2012 年。根据韩家杖子雨量站历年降雨量数据,2012 年雨量为632.1 mm,降雨量大于600 mm,符合实际情况。
4 结语
根据预测结果,预测数值与实际情况相符,可以看出对绕阳河流域洪水年模型的建立是合理的。这对该流域降雨特点的研究提供极大的便利条件,为今后该流域水文监测预警机制提供数据支撑。GM(1,1)模型在水文数据预测中的适用面十分广泛,本文主要是对韩家杖子流域洪水年进行模型建立并进行丰水年预测,同样可以适用于各区域干旱年、径流量等方面预测。但GM(1,1)模型的建立还存在一定局限性,有时会产生误差较大、数据选取不合理等方面问题,因此在应用中要注意数据处理、精度检验等方面问题。

