落实能量观 提升学科素养
——浅谈能量守恒定律在高中物理解题中的应用
云南 蒋金团
在高中阶段,解答物理学中动力学问题主要有三种方法,第一种方法是采用牛顿运动定律结合匀变速直线运动的规律求解;第二种方法是采用动量定理和动量守恒定律求解;第三种方法是采用功能关系求解。第一种方法与第三种方法的主要差别在于处理多过程问题时,牛顿运动定律只能根据不同阶段的运动性质逐段求解,而功能关系既可以分段求解,也可以全过程求解,采用功能关系处理多过程问题往往有独到之处。正因为如此,在高中物理教学中,教师应依托相关的物理模型,深度培养学生的能量观念,提升学生的物理学科核心素养。
一、常见的功能关系
功是能量转化的量度,做功的过程伴随着能量的转化,一个力对物体做了多少功,就有多少能量发生转化,因此使用能量观点解题时,首先,必须弄清楚各个力的做功情况。实际答题时,可按如下的步骤依次进行:(1)选取研究对象进行受力分析,先分析场力(重力、电场力、磁场力),接着分析弹力,最后分析摩擦力;(2)确定各个力的做功情况,若力与速度垂直则该力不做功,若力与速度同向或成锐角则该力做正功,若力与速度反向或成钝角则该力做负功;(3)根据各个力的做功情况确定对应能量的增减情况及数值;(4)利用功能关系列方程求解未知量。
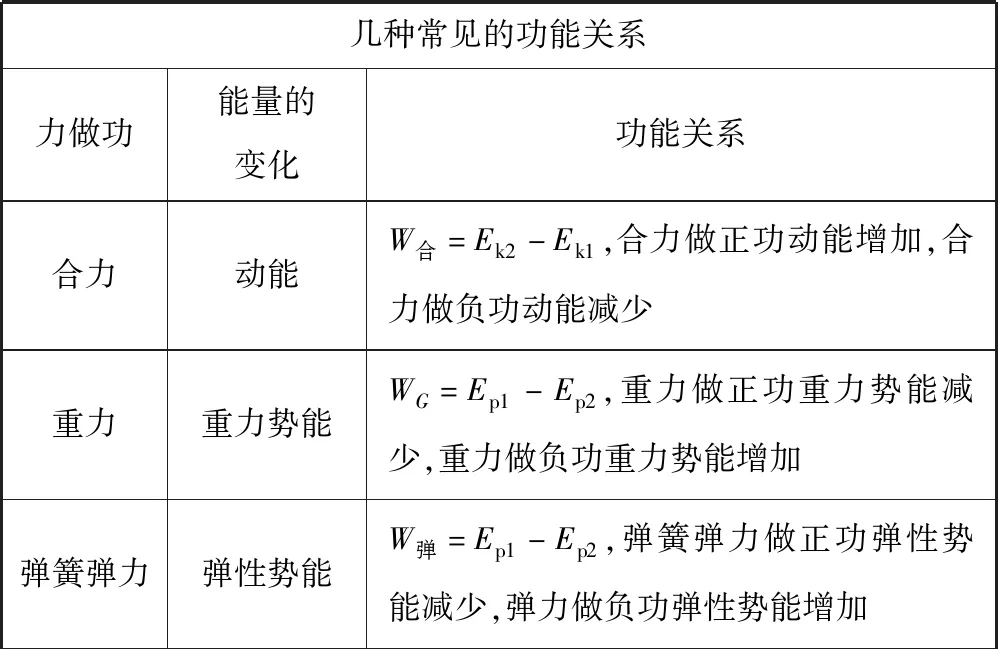
几种常见的功能关系力做功能量的变化功能关系合力动能W合=Ek2-Ek1,合力做正功动能增加,合力做负功动能减少重力重力势能WG=Ep1-Ep2,重力做正功重力势能减少,重力做负功重力势能增加弹簧弹力弹性势能W弹=Ep1-Ep2,弹簧弹力做正功弹性势能减少,弹力做负功弹性势能增加
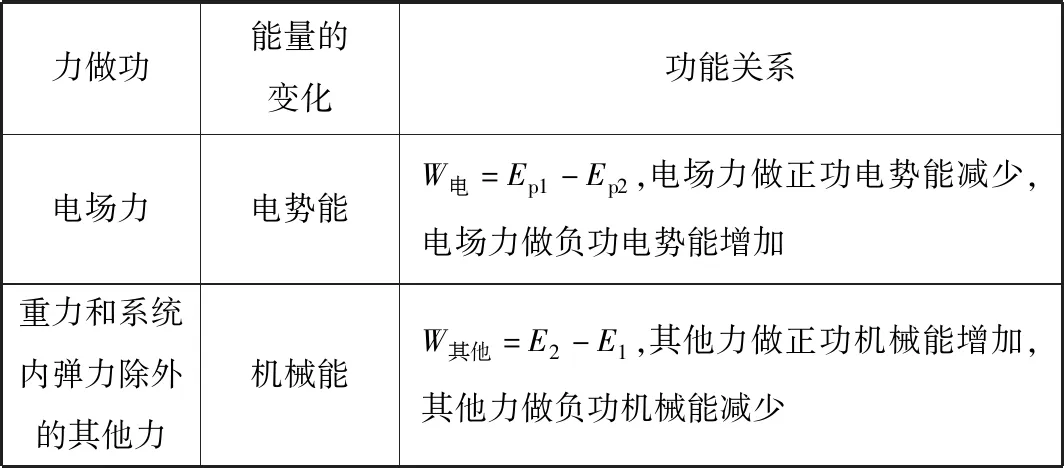
续表

( )
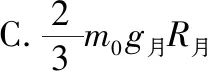

【解题总结】正确解答本题的关键点有三个:(1)准确地受力分析,弄清每个力的做功情况,进而确定合力做功属于恒力做功还是变力做功,若为变力做功,则优先考虑“动能定理”或“能量守恒定律”寻找解题突破口。本题中的探测器受到月球施加的万有引力,当探测器距离月球表面越来越高时,其所受的万有引力逐渐减小,因此本题属于变力做功问题,可选择动能定理作为解题的突破口;(2)要充分利用题目中给出的引力势能公式,根据功能关系算出万有引力所做的功,探测器升高时,探测器的引力势能增加,万有引力做负功,万有引力所做的功等于引力势能的增加量;(3)深刻理解黄金代换式的桥梁作用。
【例2】将一小球从地面上以一定的初速度竖直向上抛出,设小球的动能为Ek,小球距离地面的高度为h,小球在上升过程和下落过程中的部分Ek-h图像如图1所示,已知小球所受空气阻力大小恒定,当地重力加速度为g=10 m/s2,下列说法正确的是

图1
( )
A.从开始抛出到落回地面,小球损失的机械能为20 J
B.小球的质量为2 kg
C.小球受到的空气阻力为1 N
D.若以地面为零势能面,小球的最大重力势能为60 J

【解题总结】本题以图像为载体,考查学生对功能关系的理解及灵活应用。解答这类题,我们可按如下的步骤进行:(1)把图像中的每个点和运动过程中的每个位置一一对应,实现图像到运动模型的转化。例如,图像中的点(0 m,72 J)表示小球刚抛出时动能为72 J,而点(0 m,48 J)表示小球落回地面时的动能为48 J;(2)利用物理规律写出图像的表达式,把物理表达式和数学函数“y=kx+b”进行对照,找出斜率和截距的物理意义,难点便可突破。例如,上升过程的物理表达式为Ek=-(mg+F阻)h+72 J,该函数斜率的绝对值表示上升过程中小球受到的合力,纵轴截距表示抛出时的初动能,下落过程的物理表达式为Ek=-(mg-F阻)h+(mg-F阻)H,该函数斜率的绝对值表示下落过程中小球受到的合力,纵轴截距表示“(mg-F阻)H”。
二、滑动摩擦力做功与摩擦生热
滑动摩擦力做功(W=Ffs)和摩擦生热(Q=Ffs)是一对非常容易混淆的公式,学生之所以混淆在于他们没有区分两个公式中s的物理意义,事实上,只要准确把握好参照物,明确两个s的物理意义,这个点是不难突破的。
(1)计算滑动摩擦力做功时,分两种情况,若物体做单方向直线运动,公式W=Ffs中的s指的是物体的位移;若物体做的是往返型直线运动,公式W=Ffs中的s指的是物体的路程。
(2)计算摩擦生热时,分两种情况,若物体在运动的长木板上做单方向直线运动,公式Q=Ffs中的s指的是物体与长木板的相对位移;若物体在运动的长木板上做往返型直线运动,公式Q=Ffs中的s指的是物体与长木板的相对路程。
【例3】如图2所示,在光滑的水平地面上放置长木板B,在长木板的左侧放置滑块A,现用水平恒力将滑块A拉到长木板B的右侧,第一次将长木板B固定在地面上,此时滑块A克服摩擦力做的功为W1,两者间的摩擦生热为Q1;第二次长木板B未固定在地面上,此时滑块A克服摩擦力做的功为W2,两者间的摩擦生热为Q2,下列说法正确的是

图2
( )
A.W1
C.W1 【解析】长木板B固定时,滑块A的位移和相对B的位移大小都等于板长;长木板B未固定时,滑块A运动以后,长木板B在滑动摩擦力的作用下向右运动,此时滑块A的位移大小大于板长,而相对位移大小仍然等于板长。因为滑动摩擦力做功与位移有关,第二次过程的位移大小较大,则W1 【解题总结】解答本题的关键点是“两个区分”,首先,要区分“位移”和“相对位移”,计算滑块的位移时,以大地作为参考系,而计算滑块的相对位移时,以长木板作为参考系;其次,要区分“滑动摩擦力做功”与“摩擦生热”,滑动摩擦力做功与位移有关,而摩擦生热与相对位移有关。 【例4】如图3所示,在粗糙的水平地面上放置一质量为m=4 kg的长木板,在长木板的右端放置质量为mA=1 kg的滑块A,在长木板的左端放置质量为mB=5 kg的滑块B,两滑块与长木板之间的动摩擦因数均为μ1=0.5,长木板与地面之间的动摩擦因数为μ2=0.1。某时刻两滑块以相同速率v0=3 m/s相向运动,两滑块相遇时,A与长木板恰好相对静止,当地重力加速度取g=10 m/s2,最大静摩擦力等于滑动摩擦力,求: 图3 (1)滑块B开始运动到滑块B与长木板相对静止时,滑块B与长木板之间的摩擦生热; (2)滑块A、B开始运动时两者之间的距离。 【解析】(1)以水平向右为正方向,在滑块B开始运动到滑块B与长木板相对静止的过程中,由牛顿第二定律得 滑块A的加速度为aA=μ1g=5 m/s2 滑块B的加速度为aB=-μ1g=-5 m/s2 长木板的加速度为 以长木板作为参考系,对于滑块B,有 相对初速度为vB0相=v0=3 m/s 从滑块B开始运动到滑块B与长木板相对静止,所用的时间为 滑块B与长木板之间的摩擦生热为 Q=μ1mBg·xB相=15 J (2)在滑块B开始运动到滑块B与长木板相对静止的过程中,以长木板作为参考系,对于滑块A,有 相对初速度为vA0相=-v0=-3 m/s 此过程中,滑块A的相对末速度为 vA1相=vA0相+aA相t1=-2 m/s 此过程中,滑块A的相对位移为 滑块B和长木板共速之后,设两者组成整体的加速度为a′,由牛顿第二定律得 因为|a′|<μ1g,说明滑块B和长木板共速之后,两者将一直保持相对静止。 在滑块B和长木板相对静止到滑块A和长木板相对静止的过程中,以长木板为参考系,对于滑块A,有 两滑块开始运动时,两者间的距离为 【解题总结】本题以“滑块—长木板模型”为载体,考查学生对牛顿运动定律、匀变速直线运动规律、摩擦生热等核心知识点的综合应用能力。处理“板块模型”时,运用“相对运动”解题往往有独到之处。实际解答时,按如下的步骤进行:(1)分别对滑块和长木板进行受力分析,根据受力情况确定运动情况,需要说明的是当滑块和长木板共速时,一定要用最大静摩擦力来判断摩擦力的突变情况;(2)运用牛顿第二定律分别算出滑块和长木板的加速度;(3)以长木板作为参考系,利用公式“相对量=研究对象的量-参考系的量”计算滑块的相对初速度、相对末速度、相对加速度和相对位移等运动量,需要说明的是,计算相对运动量时,矢量的方向必须参与运算,此时规定矢量的正方向显得尤为重要;(4)将相对运动量代入运动学公式,以时间为桥梁,将滑块和长木板的运动学方程联系在一起,便可联立求解。 “弹簧模型”是考查学生物理学科核心素养的良好载体,从力的角度讲,弹簧的长度发生改变时,它对物体施加的是变力,力的变化往往涉及临界问题和极值问题,这就能很好地考查学生应用牛顿运动定律解决动力学问题的能力;从能的角度讲,弹簧的长度发生改变时,必然涉及弹性势能和其他形式的能量之间的转化,这就能很好地考查学生应用能量观点解决物理问题的能力。 【例5】如图4所示,竖直平面内固定着一个半径为R=1 m的半圆形轨道,该轨道与光滑水平面在B点平滑连接,水平面左侧的墙上固定着一个轻质弹簧,一质量为m=1 kg的滑块将弹簧的右端压缩到A点后由静止释放,滑块脱离弹簧后经过B点时对轨道的压力为自身重力的8倍,之后沿着轨道向上运动恰能通过最高点C,已知当地重力加速度为g=10 m/s2,求: 图4 (1)弹簧的右端位于A点时,弹簧的弹性势能Ep; (2)滑块从半圆形轨道的最低点B运动到最高点C的过程中,滑块与轨道之间的摩擦生热Q。 【解析】(1)设滑块经过B点时的速度为vB,此时受到的支持力为FN 由牛顿第三定律得FN=F压=8mg 联立各式得Ep=35 J 滑块从半圆形导轨的最低点B运动到最高点C的过程中,由能量守恒定律得 联立各式得Q=10 J 【解题总结】(1)弹簧将滑块推出时,滑块受到的合力是变力,匀变速直线运动规律并不适用,此时往往利用功能关系寻找突破口;(2)滑块在轨道上运动时,滑块做的是变速圆周运动,在圆周运动模型中,涉及某个位置的信息时,列向心力的来源方程,涉及研究对象从某个位置运动到另一个位置的过程问题时,列动能定理方程或能量守恒定律方程。 【例6】现有两个质量分布均匀的星球A和B,将两个完全相同的弹簧分别竖直固定在两个星球的水平桌面上,再将两物体P和Q分别轻轻放到星球A和B上弹簧的上端,两物体的加速度a与弹簧的压缩量x之间的函数关系分别如图5中的实线和虚线所示,已知星球A的半径是星球B的半径的3倍,下列说法正确的是 图5 ( ) A.星球A和星球B具有相同的密度 B.物体P和物体Q的质量之比为3∶1 C.下落过程中,物体P和物体Q的最大动能之比为1∶4 D.下落过程中,物体P和物体Q的最大位移之比为1∶4

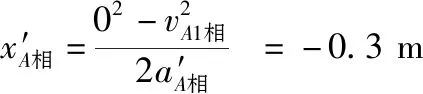
三、与弹簧有关的能量守恒问题







