Matlab应用于量子力学课程教学研究
钟志有,龙 浩,陈首部
(中南民族大学 电子信息工程学院,湖北 武汉 430074)
1 引言
量子力学是反映微观粒子运动规律的理论,已被广泛应用于宇宙学、材料学、生物学和化学等有关学科和许多近代技术中[1~7]。作为一门建立在公理体系上的科学,其理论抽象难懂、计算繁琐复杂、数学要求高,因此学习起来难度大、效果差[8,9]。Matlab是目前最为常用的科学计算软件之一,不仅使用简单、运算高效、便于扩展,而且其数值计算能力和可视化功能非常强大[10~19],因此被广泛应用于数据分析、数值计算、图像处理、模拟仿真等科学研究和教学实践中[20~25]。本文以超越方程和线性谐振子作为例子,阐述了Matlab在量子力学教学中的应用。
2 方程求解
在量子力学中,求解定态薛定谔方程时可能得到超越方程,一般采用图解法,不仅枯燥繁琐、工作量大,而且解的精度也难满足要求,这时如果利用Matlab软件处理就能迎刃而解、事半功倍。例如:由黑体辐射公式导出维恩位移定律―能量密度极大值所对应的波长λm与温度T成反比,即λmT=b(常数),并近似计算b的数值。
根据黑体辐射公式[1,5]:
ρ(v)dv=8πhv3c-3(ehv/kT-1)-1dv
(1)
利用ρ(v)dv=-ρ(λ)dλ,v=c/λ,易得ρ(λ)的表达式为:
ρ(λ)=8πhcλ-5(ehc/λkT-1)-1
(2)
令x=hc/λkT,由dρ(x)/dx=0可得:
xex-5ex+5=0
(3)
方程(3)为超越方程,利用Matlab软件求解只需在Command Window中输入如下指令即可(图1)。可见当x=hc/λkT=4.9651时ρ(λ)取得极大值,故得常数b=2.903×10-3m·K。Matlab求解超越方程,工作量明显减小。

图1 Command Window中输入的指令和运行结果
3 线性谐振子
取一维线性谐振子的平衡位置为坐标原点O,并选O点的势能为零[1],此时势能表达式为V(x)=mω2x2/2,对应的能量本征方程为:
(4)
通过无量纲变换[5],利用波函数标准条件,可得线性谐振子的能量为:
En=(n+1/2)ħω,n=0,1,2,……
(5)
相应的波函数和几率密度如下:
ψn(ζ)=Nnexp(-ζ2/2)Hn(ζ)
(6)
(7)
式(6)中,Nn为归一化常数,Hn(ζ)为厄密多项式。可见,线性谐振子的能量是分立的、均匀分布的,并且存在零点能E0=ħω/2。而对于经典的线性谐振子,ζ=asin(ωt+δ),其几率密度为:
w(ζ)=(a2-ζ2)-1/2/(2π)
(8)
为了直观分析量子数n对波函数和几率密度的影响,基于上述公式利用Matlab软件编程绘制了相关图像(图2),其中虚线为经典情况的几率密度。由图2可知,线性谐振子的波函数具有确定的宇称,n为奇数时为奇宇称,n为偶数时则为偶宇称。波函数的节点个数随量子数n增加而增加。另外,量子数n较小时几率密度与经典情况没有相似性,n增大时相似性随之增加。当n=15时,量子和经典的两种情况在平均上基本符合,差别在于|ψ(ζ)|2迅速振荡而已。Matalb模拟结果与理论分析完全一致[1,5]。
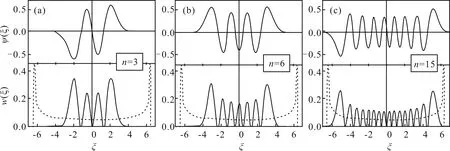
图2 量子数对波函数和概率密度的影响
4 结语
本文针对学生学习量子力学所遇到的实际问题,以超越方程和线性谐振子作为实例,利用Matlab软件进行求解分析和可视化处理,从而大大简化了繁琐的计算过程,将抽象难懂的理论知识变得形象直观,因此有利于强化物理实质讲解、优化课程体系、激发学生学习兴趣,对于提高量子力学教与学的效率都具有非常重要的作用。

