基坑支护结构深层水平位移监测最佳间距设置的研究
何 钦,丘北刘,张记峰
(广东省建设工程质量安全检测总站有限公司 广州510500)
0 引言
目前基坑工程中的桩体深层水平位移监测主要依靠测斜管和测斜仪完成。按照《城市轨道交通工程监测技术规范:GB 50911-2013》[1]的要求,深层水平位移监测自下而上以0.5 m 或1.0 m 的间距逐段量测。实际工程中一般采用0.5 m 的监测间距,而当桩身较长时,深层水平位移监测就会成为一项费时费力的工作。如果能够将监测设点的密集度降低,无疑可以节省较大的人工和时间成本。然而,桩体水平位移线形可有多种形式,不同形式的曲线危险点出现位置均不一致。因此,如何在扩大测试间距的同时保证测得数据不会漏掉关键的测试点成为一个重要难题。
为此,本文对相关研究进行了调研。其中,郑磊等人[2]认为,在测斜管足够深的前提下,适当增大测点间距对墙体位移的精度影响可以忽略不计;高峻合等人[3]和蔡干序[4]发现2 倍导轮距(1.0 m)的测斜数据与1 倍导轮距(0.5 m)的测斜数据部分存在偏差;胡均等人[5]和张园园[6]则发现在深基坑中测斜间距采用0.5 m 或是1.0 m 对数据分析的影响不大;郑晓栩[7]认为1.0 m 间距的测斜数据不可靠,需要利用0.5 m 测点数据进行部分修正;吴立成[8]在基坑围护结构深层水平位移监测及规律研究中提到,在测斜上半段和下半段的斜率一致的情况下,可以适当放大测段间距,但仍然需要辅以0.5 m 测段间距的数据作为修正及校核。以上学者均对测斜间距进行了研究,但却得出了大相径庭的结论,这可能是由于上述工作大部分仅基于测斜仪的工作原理,直接采用测试不同的测试间距数据进行对比,而没有根据不同的测斜线形进行分析,也没有对桩体的受力状态进行讨论。
为了弥补目前研究的不足,在上述研究的基础上,本文基于多组基坑桩体深层水平位移的监测数据进行了研究,对不同线形水平位移测试结果进行了隔点提取分析。利用不同间距的水平位移测试数据以Spline插值函数插值得到以0.5 m 为间距的测点结果,并与实际0.5 m 为间距的测试结果进行对比,对增加测点间距监测的可能性进行了讨论。
1 研究方法和数据处理
为了确定深层水平位移的最佳间距,本文选用了多个工程且测斜孔深度在21.5 m以上的深层水平位移实测数据,对不同形状的线型曲线数据进行研究。其中,曲线的连接方式采用Spline 插值来完成,通过Spline插值处理后且测试间距大于0.5 m 的曲线数据,与测试间距为0.5 m的曲线数据之间的差别进行对比。若测试间距大于0.5 m 的测试组的Spline 曲线数据与测试间距为0.5m测试组的曲线数据间差别较小,则说明在测斜管深度大于21.5 m 时该间距可以代替0.5 m的间距进行监测,从而达到减少时间成本和降低劳动强度的效果,扩大测试间距在经济上也更具优势。
1.1 Spline插值函数选用说明
桩体的水平位移主要因桩身水平方向受弯产生,而通过结构力学知识[9]我们可以了解到,均质线性材料由于受弯产生的位移,其计算公式与其杆长的三次方成正比。均质线性桩体某点处的水平位移一般计算公式可表示为:

式中:y为桩体某点处的水平位移;k为与桩体该点位置坐标等几何特征相关的无量纲系数;F为作用于桩身某点的外作用力大小;l为桩长;E为桩体变形模量(材料均质线性时E为定值);I为截面距。而Spline插值实际为三次方幂函数插值,并且插值通过曲线上的4个控制点实现。由于Spline插值函数与上述位移函数线性一致(均为坐标的3次函数且连续光滑),当散点间隔减小时,插值出来的数据点也越接近实际桩体水平位移分布曲线。换言之,如果桩体材料本身非均质线性,或存在非连续的非均质点或区域,则水平位移分布曲线本身会存在许多非光滑的点。此时,Spline函数便不一定能很好地插值出与真实情况一致的曲线。
1.2 分析数据说明
本文采用的水平位移监测数据根据形状的不同可定义为:蝶形、反S形、开口形、抛物线形以及激凸形5大类。分析时,对原有间隔为0.5 m 的测试数据进行隔点提取,分别将间距为1.0 m、1.5 m 和2.0 m 的数据提取出来进行Spline 插值;插值后的曲线用于与原曲线进行对比。
1.3 曲线处理结果对比
不同形状的测斜曲线在应用Spline插值方法补全数据的同时,可能存在不同程度的偏离情况。因此,对不同形状的测斜数据分别以不同间隔点进行插值处理,以便于分类讨论。插值得到的测斜曲线对比图按不同形状分类别给出如图1~图5所示。
通过观察上述不同类型测斜曲线的不同间距数据插值结果可以发现,1.5 m 和2.0 m 两种测点间距无论何种测斜曲线形,利用Spline 插值后的曲线数据与0.5 m 间距曲线数据对比偏差都过大,因此,以上两种测试间距在实际工程中都不具备实现的可能性。只有测点间距设置为1.0 m时,利用Spline插值得到的完整曲线与0.5 m 间距测得数据的Spline 插值曲线相符度较高。尤其是开口形和抛物线型两种,1.0 m 间距和0.5 m 间距的Spline 插值曲线几乎看不出偏差,如图3a和图4a所示。然而,在其他的包括蝶形、S形和激凸形曲线中,即使是1.0 m 与0.5 m 的曲线对比中也能发现较明显的偏差点,如图1a、图2a和图5a所示。因此,为更全面地考察扩大间距监测的合理性,需要对蝶形、S形和激凸形这3种线形的数据进行进一步的偏差分析。

图1 蝶形曲线Spline插值曲线对比Fig.1 Comparison of Butterfly Curve Spline Interpolation Curve


图2 反S形曲线Spline插值曲线对比Fig.2 Comparison of Spline Interpolation Curves of Inverse S-shaped Curve

图3 开口形曲线Spline插值曲线对比Fig.3 Comparison of Spline Interpolation Curves of Open Curve
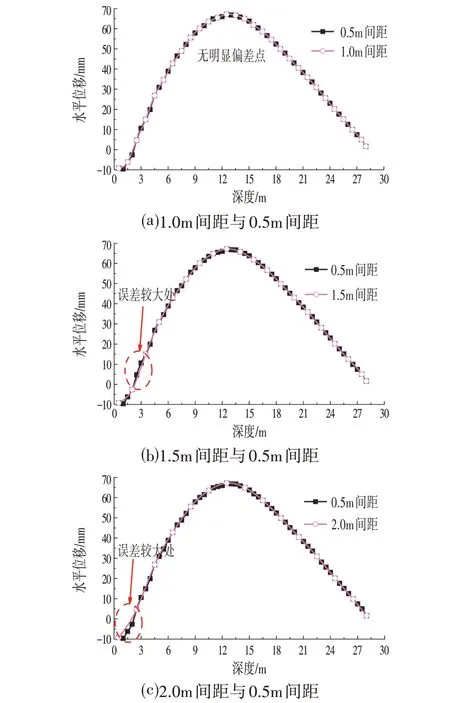
图4 抛物线形曲线Spline插值曲线对比Fig.4 Comparison of Parabolic Curve Spline Interpolation Curve
2 曲线偏差的应力反分析

图5 激凸形曲线Spline插值曲线对比Fig.5 Comparison of Spline Interpolation Curves of Convex Curve
对上述蝶形、S 形和激凸形3 种线形测点数据的插值进行偏差分析,利用Abaqus 的应力分析模块进行。首先,在1.0 m间距测点数据经Spline插值得到的完整曲线中提取出间距为0.5 m 的水平位移数据点;再参考位移法[10],利用提取得到的数据点和以0.5 m间距测得的原始数据点分别建立梁单元水平位移模型,利用数据点的水平位移作为位移边界条件施加在梁单元上,对其受力情况进行反分析。其中,考虑到监测数据为到达某一深度停止而并非全长,因此将梁单元相当于桩底位置处设立仅限制纵向位移(重力方向)的单向约束。梁单元的局部坐标在长度方向上选为与整体坐标的y轴正方向一致。以此方法建立模型计算得到的应力结果可以逼近桩体真实的受力情况,已知位移点数越多则计算结果越接近实际。以下对上述反分析方法得到的3 种不同类型数据点的模型计算结果分别进行分析和讨论。
蝶形大主应力计算结果如图6a、图6b所示,小主应力计算结果如图6c和图6d所示。

图6 蝶形大、小主应力计算结果Fig.6 Calculation Results of Butterfly Shaped Large and Small Principal Stresses
从计算结果的变形曲线来看,2 种数据分析得到的桩身变形曲线相符程度较高,看不出明显线形差别。就应力计算结果来看,无论时大主应力还是小主应力(分别代表着梁单元截面上的最大受拉和受压应力),1.0 m 间距得到的计算结果均小于0.5 m 间距结果。这说明,蝶形数据扩大间距测量得到的结果在应力分析中偏于危险。但就最危险点的分布位置来看,0.5 m 计算云图的大主应力最大区域为15.634 20~16.169 07 m(见图6a),而1.0 m 的计算结果则为14.732 95~16.307 09 m间(见图6b);0.5 m计算云图的小主应力最大区域为18.354 43~18.920 40 m(见图6c),而1.0 m 的计算结果则为18.389 81~18.981 98 m(见图6d)。这表明,蝶形组利用1.0 m 间距数据找到的桩体最不利位置范围基本可以包含0.5 m 数据求得的最不利位置。
反S 形大主应力计算结果如图7a、图7b 所示,小主应力计算结果如图7c、图7d所示。

图7 反S形大、小主应力计算结果Fig.7 Calculation Results of Inverse S-shaped Large and Small Principal Stresses
与蝶形组类似,从计算结果的变形曲线来看,反S形的2种间距数据分析得到的桩身变形曲线相符程度也很好,看不出明显线形差别。就应力计算结果来看,无论是大主应力还是小主应力(分别代表着梁单元截面上的最大受拉和受压应力),1.0 m 间距得到的计算结果均小于0.5 m间距结果。这说明,反S形数据扩大间距测量得到的结果在应力分析中也偏于危险。至于其最危险点的分布位置,0.5 m 计算云图的大主应力最大区域为14.457 85~14.679 16 m(见图7a),1.0 m的计算结果则为14.373 50~15.074 11 m(见图7b);0.5 m计算云图的小主应力最大区域为20.921 54~21.050 38 m(见图7c),而1.0 m 的计算结果则为20.437 35~20.630 62 m(见图7d)。这表明,反S 形组利用1.0 m 间距数据找到的桩体最不利位置范围也可以包含0.5 m 数据求得的最不利位置。
激凸形大主应力计算结果如图8a、图8b 所示,小主应力计算结果如图8c、图8d所示。

图8 激凸形大、小主应力计算结果Fig.8 Calculation Results of Large and Small Principal Stresses of Convex Shape
激凸组2种间距数据分析得到的桩身变形曲线相符程度也很好,看不出明显线形差别。就应力计算结果来看,1.0 m 间距得到的应力计算结果均小于0.5 m间距结果。可见,激凸形数据扩大间距测量得到的结果在应力分析中也偏于危险。0.5 m 计算云图的大主应力最大区域为10.212 44~10.377 98 m(见图8a),1.0 m的计算结果则为9.431 84~9.625 92 m(见图8b);0.5 m计算云图的小主应力最大区域为11.308 43~11.491 10m(见图8c),而1.0 m 的计算结果则为11.418 32~11.629 53 m(见图8d)。根据最危险点位置的分布情况可以看出,虽然激凸形组利用1.0 m 间距数据找到的桩体最小应力最不利位置与0.5 m 数据计算结果较为接近,但1.0 m 间距数据找到的桩体最大应力最不利位置则与0.5 m 数据计算结果产生了较大偏差(相差1 m左右)。
上述结果说明,利用Spline插值方法补全数据,可以使得到的数据与0.5 m 间距测斜数据保持一致的线形。此外,虽然反S 形和蝶形的0.5 m 间距和1.0 m 间距测斜数据Spline 曲线存在个别误差较大点,但对其用于预测桩体最不利位置的影响不十分明显;利用1.0 m 测斜数据Spline 插值得到的位移数据进行应力反分析找寻最不利位置的结果可以包含0.5 m 组分析得到的最不利位置。但是,扩大间距测试并利用Spline 插值补缺数据也存在一定的缺陷。例如,扩大间距的位移数据反分析得到的应力分析结果均小于原始数据的应力分析结果;当曲线存在较明显的激凸点时,根据扩大间距的位移数据反分析得到的最不利位置可能产生较大偏移(本文为大致为1 m)。如第二节所述,Spline插值方法线性与挠度曲线相一致,若桩体材料均质均匀则线性应多表现为开口形和抛物线形等较光滑的曲线。因此,本文蝶形和反S 形中扩大间距的Spline 曲线显示的数据偏差,可能是由于桩体制作时的初始缺陷引起的水平位移凸变点而导致的。
3 结论
为了在深基坑工程深层水平位移监测中适当增加监测间距,以达到降低时间成本、人工成本及劳动强度的目的。本文利用Spline 插值的方法分别对1.0 m、1.5 m、2.0 m 测试间距的多种测斜数据进行插值处理,然后将Spline插值完成的数据分别与0.5 m测试间距的实测水平位移数据进行对比。在数据对比过程中发现,只有开口形和抛物线形的1.0 m间距Spline插值曲线与其对应的0.5 m 测试间距水平位移实测曲线相符性较高,另外的蝶形、反S形和激凸形3种线形的插值曲线与0.5 m 测试间距的数据偏差较大。为了进一步验证数据的相符性,本文对蝶形、反S形和激凸形3种曲线采用Abaqus的应力分析模块进行了应力反分析验算;通过上述几种不同类型的插值数据与0.5 m测试间距的水平位移实测数据的对比分析结果得出以下主要结论:
⑴当测斜曲线不存在明显激凸点时,以1.0 m 间距的监测数据进行有限元应力反分析找出的桩身最危险点所在位置,与0.5 m 间距监测数据进行反分析得到的最危险点位置吻合度较高。因此,以1.0 m 为间距替代0.5 m 间距进行监测以控制工程的安全是具有一定可行性的。
⑵若扩大间距测得的测斜结果显示的位移变化曲线存在明显的激凸形状,即明显区别于三次幂函数线形的凸起点,则说明桩体可能存在明显的初始缺陷,应增加测点补充监测以全面监控桩体变形。
⑶利用扩大间距测得的测斜结果进行Spline 插值补充后,再进行有限元应力反分析得到的应力偏小于0.5 m间距数据的计算结果,应考虑乘以一定的扩大系数后再进行分析和设计计算,以保证工程安全。
⑷本文所用最短桩的测点长度为21.5 m,而1.0 m的测试间距大于最短桩总测试长度的4.5%,可见本文所用分析数据均为桩身较长的情况。因此,本文所得结论适用于测点深度在21.5 m 以上的长桩分析,在测点深度21.5 m 范围以内的水平位移监测数据应用本文方法进行处理的适用性仍待考察。

