质量阻尼比对圆柱体流致振动捕能效率的影响
白旭,韩传煜,孙海
(江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003; 2.哈尔滨工程大学 航天与建筑工程学院,黑龙江 哈尔滨 150001)
流致振动广泛地存在于许多工程领域中[1],作为储量巨大的清洁能源,海流能与风或海浪相比,具有季节性、周期性,其流动状况高度可预测。但近海岸洋流流速往往较低,导致难以利用传统方式获取海洋能量。流致振动捕能技术正在成为可再生能源发电的可行解决方案,需要开展重大的研究、开发和部署计划,才能在该领域取得真正的产业成功[2]。近年来,许多学者开始研究利用流致振动获取低流速下海洋动能的发电方式。
流致振动是指流体流经固体时会对固体表面施加交替相间的流体力,使得固体发生往复运动,而固体的往复运动又改变流体流态,进而改变作用于固体表面的流体力[3]。尽管有关流致振动发电的研究并未形成系统的研究体系[4],但仍取得了成果。Belloli等[5]比较了临界流动状态下涡激振动与亚临界振动的特征。Sun Hai等[5-7]研究具有端部弹性约束的刚性振子的流致振动,对幅度响应,频率响应,能量收集和效率的实验结果进行了介绍和讨论,并使用2个汽缸串联进行实验,给出了能量收集和效率的实验结果、推导出最优功率的包络。罗竹梅[8]提出了一种结合并列和串列构形的矩形布置四圆柱振动系统,并提出机械耦合的概念描述这种系统的动态特性,将由4个圆柱组成的振动系统整体视为一个质量-弹簧-阻尼系统。Kim等[9]证明了交替提升技术(ALT)转换器是一种能量吸收装置,可有效地在速度低至1.0~1.5 m/s的水流中工作,这是目前水车和涡轮机无法达到的速度范围。燕翔[10]分析了电机参数、机械参数及振子截面参数对三棱柱振动模式、能量利用的影响,明确了三棱柱在流致振动能量利用上的优势。练继建等[4]剖析了研究当中存在的各类问题,并对流致振动能量利用的研究方向提出了建议。这些研究集中在物理结构、流速等参数对振动的影响上,尚未存在对振动捕能效果的组合优化的研究。本文工作是研究在现有非理想条件下,所能达到的能量转化率最大值,即最优捕能效率值。
1 振动能量获取的数学物理模型
1.1 能量的获取过程
对于本文所建立的流致振动模型,其运动中产生的可利用能量经历了2次削弱的过程:1)振动系统获取流体动能时,有一部分流体动能耗散在振子尾流粒子的碰撞、摩擦中,还有一部分流体未参与做功;2)振动系统获取的能量会有一部分损失在振动系统机械部分的摩擦中,剩下的部分才是可以加以利用的机械能,也即输入发电机的能量。能量转化过程如图1所示。

图1 水流能量的利用流程Fig.1 Flow of water flow energy
1.2 振子物理模型及受力分析
计算采用的振子直径D=0.1 m,展向长度L=1 m,振子表面光滑,由2支拉压弹簧连接在支架上,弹簧刚度为K=500 N/m。模拟质量比m*取1.1、1.4、1.7、2.0这4个数值,阻尼比ξ从0.03~0.21每隔0.03取值一次,总计取7个值。对以上28种情况,约化速度从2~12,间隔0.1取值计算。
在流致振动过程中,振子在竖直方向受3个力:即弹簧拉压力Fspr、结构及水流的阻力Fdamp、流体动压力FFluid。
如图2所示,当振子处于平衡位置以下且运动方向向下时,其加速度方向向上。故可以得到等式:
mosca+Fspr+Fdamp=FFluid
(1)
整理得:
(mosc+ma)Y″+(cfluid+cstructure)Y′+KY=
(2)
式中:cFluid为流体附加阻尼;cstructure为振动结构的总阻尼;Γ为离散点涡强度;U为水流的来流速度;D、L为圆柱振子的直径、长度;ma为振子的附加质量;流体力FFluid根据文献[13]讨论得到。
1.3 振幅比A*、频率比f*计算
引入涡强方程Γcos(2πfstt)=βUDq、无量纲位移y=Y/D、无量纲时间τ=tωst,化简式(2)得到振子运动方程;引入范德波尔方程描述无量纲漩涡强度q,得到升力荷载变化方程。二式相互耦合,联立得[14]:
(3)
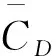
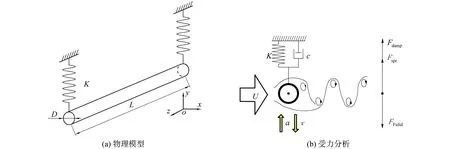
图2 单自由度振子物理模型及受力分析Fig.2 Physical model and force analysis of single degree of freedom oscillator
振幅比A*是无量纲位移y的极值,振幅比f*是振子振动频率与振子在水中的自振频率的比值。使用四阶龙格库塔法求解式(3),时间步长取0.1,得到不同约化速度下振子随周期振动的振幅比A*,对震荡的时历曲线进行傅里叶展开,求得频率比f*。
1.4 功率计算
1.4.1 流体功率计算
水流做功的功率可以根据水流对振子的压力乘以水流流速求得。根据伯努利方程,水流产生的动压强为(ρU2)/2。常见的水流功率的计算方式有2种,即水流压强作用面S取振子与流体直接接触面的投影D×L,或取振子振动过程扫过的面积(2A+D)×L。这两者并无本质区别,只是对流体动能利用的关注角度不同。本文采用后一种方案,且因连杆在水流方向的投影面积相比圆柱振子的投影面积可以忽略不计,忽略水流对连杆部分的作用力,取水流压强的作用面为S=(2A+D)×L。水流功率表示为:
(4)
1.4.2 振子捕能功率计算
将式(2)流体附加阻尼项移到等式右侧,得到:
(mosc+ma)y″+cstructurey′+Ky=
(5)
式(5)右侧即水流力与流体摩擦的差值,左右相等,故左侧部分积分即可得到振动系统捕获的能量,而后再除以周期时长,即得到流体的平均有效功率。振子捕能包含振动系统的机械能、振动系统机械摩擦损耗2部分。其数值上与与水流对振子做的功相等。对能量及功率的计算为:
cstructurey′+Ky)y′dt
(6)
根据简谐理论,振子运动位移y随时间呈简谐变化,即y=Asin(2πfosct),其中振子的振动主频为fosc,其值为Tosc=1/fosc。在稳定振动中,液体与振子发生共振,根据结构动力学共振的规律,此时的振动主频与升力主频相等,即fosc=fFluid。
根据三角函数的奇偶性、周期性,含有y、y″的项积分后为0,代入式y、y′、y″,化简为:
(7)
1.5 捕能效率计算
由于流量守恒,通过发电装置的流体速度不会发生突变,电机转换的能量仅由压强差提供,因此流体能量损失天然地存在一个上限,即贝茨极限。在桨叶式发电装置中贝茨极限取59.3%。此外,因为尾流粒子间、流体固体间的摩擦,振子不能充分利用水流本身的能量损失,因此振动系统对水流能量的利用率还要小于贝茨极限。定义振子捕能功率与流体损失功率的比值为捕能效率,表达式为:
(8)
式中:质量比m*、阻尼比ξ为结构参数;振幅比A*、频率比f*为流固耦合参数;约化速度Ur为流体参数。流固耦合参数与流体、固体参数均相关,无法直接获得,计算过程见2.3节。
2 捕能效率的影响分析
2.1 模型可靠性验证及计算方案
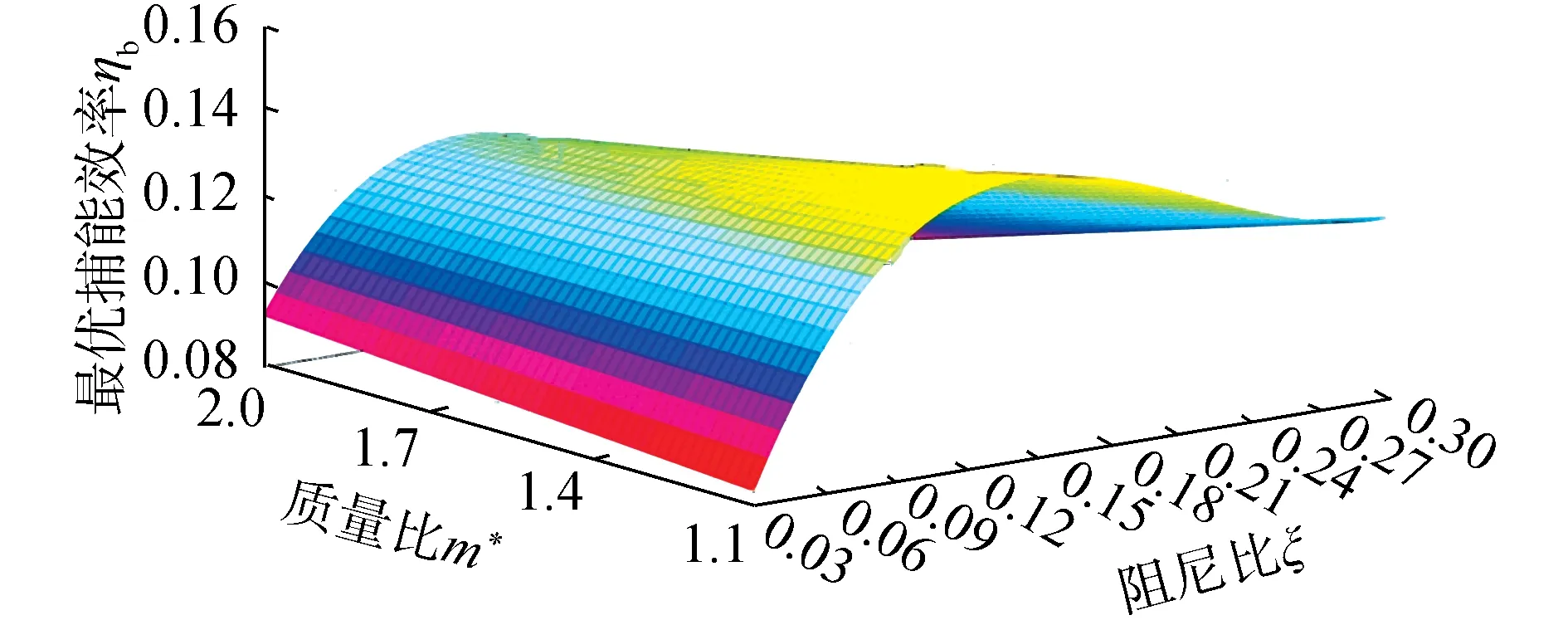
Khalak等[19]进行了m*=2.4、m*ξ=0.013的低质量比、低阻尼比物理实验;罗竹梅[8]采用SSTk-ω高雷诺数湍流模型在相同的质量比、阻尼比下进行数值模拟。本文在相同条件下,使用尾流振子模型计算约化速度2 振子在不同约化速度下的3种捕能效率曲线如图4所示。从图中可以看出,本文模拟的曲线走势与文献结果较好吻合,最大捕能效率介于文献[19]与文献[8]的实验、模拟结果,且极为接近。如表1所示,模拟的最大捕能效率与文献结果的误差分别是7.8%和23.3%,这说明了本文模拟方法的可靠性。模拟振动在Ur=4.5时获得最大捕能效率2.58%,而参考文献分别在Ur=4.5和Ur=4.6时对应取得最大捕能效率。相比下,模拟计算的整体捕能趋势均略微滞后,这可能是范德波尔经验参数取值偏小的缘故。 图3 m*=1.4,ξ=0.03,Ur=4时振子时历曲线及频谱Fig.3 Curve of time and spectrum of oscillator vibration at m*=1.4,ξ=0.03,Ur=4 表1 计算结果可靠性验证表Table 1 Reliability verification table of calculated results 图4 各约化速度下振子捕能效率Fig.4 Energy capture efficiency of oscillator at different reduction velocities 根据模拟结果,振子共振稳定后的横向振动响应近似正弦规律的谐波振动[8],取模拟计算的最后19个周期,以分析质量比、阻尼比对振子振幅比、频率比、捕能效率的影响,并总结其相互关系。 随约化速度的增加,不同质量比、阻尼比条件下的振子振幅比先增加后降低,质量比、阻尼比越低,振幅越大。记取最大振幅比的约化速度为最佳Ur,则振子的最佳Ur集中在6.3~6.9。最佳Ur值同阻尼比几乎没有关联性,但会随着质量比的增大稍稍提前。此外振幅比的变化率与质量比无关,但随着阻尼比的减小,振幅比增大得越来越快。 频率比同约化速度成正相关,其增大变化率经历了陡峭-平缓-陡峭的过程。平缓阶段4 由图5(a)知,平缓区间内的频率比与质量比无关。此外,不同阻尼比条件下频率比随约化速度的变化可以分成2个区间。区间一为3.3 图5 不同m*、ξ下振子A*、 f*随Ur变化变化图Fig.5 Variation diagram of oscillator A*, f* with Ur under different m*, ξ 不同质量比、阻尼比下振子捕能效率随约化速度的变化情况如图6所示。 图6 不同m*、 ξ下振子的捕能效率Fig.6 Energy capture efficiency of oscillator under different m*, ξ 1)总体而言,当约化速度处于4.5~6.4时,多数振子捕能效率η>10%,能量利用率较高。最大捕能效率见图6(a),m*=1.1、ξ=0.15时,捕能效率η=14.27%,此时Ur=5.1。 2)在趋势上,捕能效率η随约化速度的增加先增加再降低,在约化速度Ur=5.3附近取得最大值,定义η取最大值对应的Ur为最优约化速度,此刻捕能效率称为最优效率ηb。效率值η在远离取最优Ur处变化平缓,在最优Ur邻域也有较小变化率形成的缓和段,但在邻域外侧随Ur变化的程度尤为激烈。同图5的锁定区间比较,最优邻域恰好位于稳定共振区域,而位于进入、退出共振段区域的邻域外侧,捕能效率变化较大。 最优Ur的位置随阻尼比的增大微微增大,与质量比的取值无关。 3)最优效率ηb随质量比的变化见图7,阻尼比ξ较小时,ηb与m*正相关;ξ较大时,ηb与m*反相关。这是由于随着阻尼比的增大,振幅比迅速变小,同时频率比在Ur=5.1附近几乎没有变化。 图7 最优效率ηb随质量比、阻尼比变化Fig.7 Optimal efficiency ηb varies with mass ratio and damping ratio 4)振子阻尼比较大时,最优效率ηb随m*的变化越剧烈,从图7可看出,对于不同的m*,均存在ξ使ηb取极大值。如式(8)所示,这是因为阻尼比较小时,阻尼比本身对效率的影响较大;随着阻尼比增大,较大的阻尼比导致振幅比迅速减小,振幅比成为影响效率η的主导因子。不同质量比下取得最优效率的阻尼比数值可以由式(10)确定。 使捕能效率最大的阻尼比随质量比的变化而改变,为获取最优捕能效率,需要在模拟前估算最优阻尼比数值。用最小二乘法对ηb作关于m*、ξ的多项式曲面拟合,从而求解最优阻尼比,如图8所示。 图8 不同质量比、阻尼比变化下的最优效率ηbFig.8 Optimal efficiency ηbunder different mass ratio and damping ratio 曲面方程: ηb=0.707 6ξ2m*+13.54ξ3-0.419 2ξm*- (9) 拟合的复相关系数R-square=0.975 3,均方根误差RMSE=0.003 007,误差平方和SSE=0.000 298 4,故式(9)可以准确地描述质量比、阻尼比发生改变时,最优捕能效率ηb的变化趋势。 对式(9)右侧取关于ξ的偏导,并使其为零,得到关于m*、ξ的等式(10),即某一m*下取得最佳效率ηb的阻尼比ξ求解公式: (10) 分别代入m*=1.1到2,得ξ=0.148、0.138、0.128、0.117,符合对图6的预测。这也间接验证了式(9)的可靠性。 将m*=1.1、ξ=0.148代入式(9),得ηb=14.50%,即计算区域内的最大捕能效率。 1)振子的捕能效率峰值早于振幅比的峰值出现,这是由于振幅比、频率比的增长速率较约化速度的增长速率变化较小的缘故。 2)根据模拟结果,振子在Ur=5.1、m*=1.1、ξ=0.15时,捕能效率取最大值ηb=14.27%;根据经验公式,振子在m*=1.1、ξ=0.148时,捕能效率取最大值ηb=14.50%。 3)捕能效率随约化速度的变化曲线存在最大值,最佳捕能效率对应的约化速度Ur位于区间[5.0,5.3]。 4)在式(9)所处的低质量比区间上,最优捕能效率与质量比成反相关,质量比越小捕能效率越高;但阻尼比存在使捕能效率达到最大的极值,其值随着质量比的增大,由0.093降低至0.068。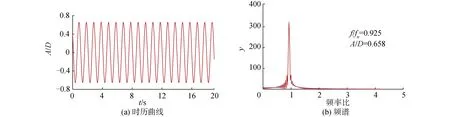


2.2 质量比、阻尼比对振子振幅比、频率比的影响

2.3 不同质量比、阻尼比下捕能效率的分析

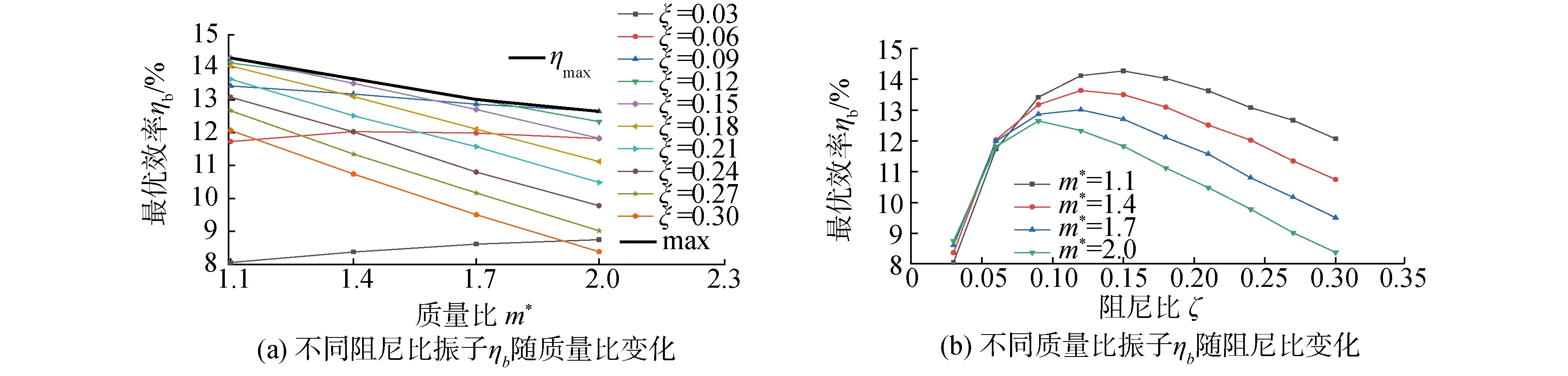
2.4 最优阻尼比分析
9.734ξ2+0.021 38m*+2.207ξ+0.015 35
(2≤Ur≤12;1.1≤m*≤2;0.03≤ξ≤0.3)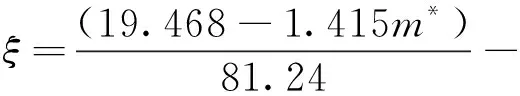
3 结论

