不同干密度压实黄土的非饱和渗透性曲线特征及其与孔隙分布的关系

李 华，李同录，张亚国，李 萍，范江文

（1.长安大学 地质工程与测绘学院，陕西 西安 710054；2.黄土高原水循环与地质环境教育部野外科学观测研究站，甘肃 正宁 745399；3.长安大学 建筑工程学院，陕西 西安 710054）

1 研究背景

黄土地区平山造城工程形成了大量的高填方场地。这些填方的压实黄土在水分入渗条件下容易产生湿陷、不均匀沉降等工程地质问题，因此有必要对压实黄土的非饱和渗流特性进行研究。

非饱和渗透系数是随吸力或含水率变化的一个参数，吸力或含水率与渗透系数的关系称为非饱和渗透性曲线。非饱和渗透性曲线可以用试验的方法直接测量或用其简单物理参数预测确定。常见的用于预测渗透性曲线的模型有许多，包括Gardner模型[1]、Chillds & Collis-George模型[2]和van Ge⁃nuchten模型[3]等，近年来孙大松等[4]、陶高粱等[5]建立了用孔隙分布特征预测非饱和土的渗透性曲线的模型。直接测量的方法有稳态法与瞬态法。稳态法保持流量、水力梯度、含水率不变，瞬态法上述参数均随时间变化。常见的稳态法包括常水头法、常流量法和离心法等。Klute[6]最早使用常水头稳态法，他通过控制试样的吸力，测量水量来得到渗透系数。梁爱民[7]、徐永福等[8]在此基础上设计了测量更为精准的新型的稳态渗流装置。李永乐等[9]用改进的非饱和三轴仪测量了非饱和土的渗透性曲线。但稳态法往往十分耗时，瞬态法则相对稳态法更快一些。瞬态剖面法是最常用的瞬态法，该方法将试样装在一圆筒中，使水流自土柱一端流向另一端，沿着土柱布置一系列探头，定期测量各个测量点的含水率和吸力，从而得到不同时刻含水率与水头剖面。通过含水率和水头剖面计算得到流速与水力梯度，最后用达西定律计算渗透系数。覃小华等[10]用垂直土柱入渗试验测得压实黄土0～100 kPa 的渗透系数，用水分传感器测得含水率与单独测得的土水特征曲线得到基质吸力。王红等[11]也用了垂直土柱入渗法，不同的是含水率是从土柱中取少量土烘干获得。Stormont 等[12]、Choo 等[13]用张力计传感器及含水率传感器分别测量吸力与含水率，从而获得渗透系数。李华等[14]提出了基于滤纸法的瞬态剖面法来测量非饱和渗透性曲线，该方法将滤纸法与瞬态剖面法结合，测得的吸力量程可以达到105kPa，远大于传统方法的量程，几乎可以测得完整的渗透性曲线，且得到完整的渗透性曲线只需一周左右，因此本文用该方法来测试压实黄土的渗透性曲线。

少数研究对不同干密度土壤的渗透系数进行了讨论。王铁行等[15]用水平土柱入渗法测得了不同干密度下黄土的非饱和渗透性曲线。认为含水率较大时，干密度对渗透系数影响显著，而含水率较小时干密度对渗透系数几乎无影响，但其未能直接测得用来计算水力梯度的吸力，而是用离心机测得的土水特征曲线间接计算获得。姚志华等[16]用水平和竖直土柱法测试了原状与压实黄土的渗透系数，其装置可直接测得吸力与含水率，压实黄土部分试验表明不同干密度的压实黄土干密度越大，渗透系数越小，但其装置未能测得大吸力范围（＞300 kPa）的渗透系数；另外认为低含水率区干密度对渗透系数的影响要大于高含水率区，这一结论与王铁行等[15]不同，可见不同学者对干密度与压实黄土渗透系数的关系认识仍未明确。马亚维等[17]用Chillds & Collis-George模型预测原状及压实黄土的渗透性曲线，认为黄土非饱和渗透系数减小趋势随着干密度增大而减小，但在残余含水率附近的渗透系数基本相同，但其渗透系数是模型预测所得，未能直接测得，且其测量范围仍较小（0～103kPa）。综上所述，以往对于不同干密度压实黄土渗透系数的研究较少，测量范围也有限（103kPa 以下），且未能从微观孔隙方面分析其渗透系数变化原因。

本文用李华等[14]提出的基于滤纸法的非饱和渗透试验实测了3种不同含水率压实黄土的渗透性曲线，该方法能够同时测得土壤的含水率与吸力，从而直接计算得到渗透性曲线，且能得到较大吸力范围（0～105kPa）的渗透性曲线。对所得3种压实黄土的非饱和渗透性曲线，分析了其形态特征及干密度对渗透性曲线的影响，并用各自的孔隙分布曲线解释了渗透性曲线的形态特征及差异的内在机理。

2 土样

试验土样取自延安新城某工程现场，为离石黄土下部顶层L6。通过室内常规试验测得该原状黄土样的基本物理参数如表1。

表1 延安L6原状黄土的基本物理参数

另外用激光粒度仪测得其粒径级配曲线如图1。从粒径级配累积曲线可以看出，该土样中黏粒成分（＜0.005 mm）占10.9%，粉粒成分（0.005～0.05 mm）占66.7%，砂粒成分（＞0.05 mm）占22.4%。为粉质黏土。不均匀系数Cu为7.4，曲率系数Cc为1.5。另外对土样进行了标准击实试验，测得其击实曲线如图2，可见土样的最大干密度为1.79 g/cm3，最优含水率为16%。

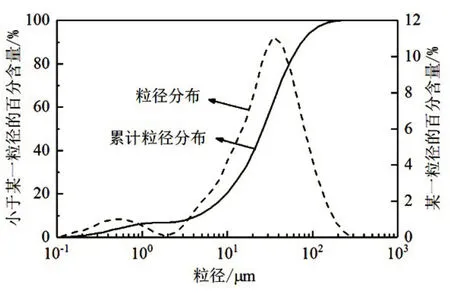
图1 粒径级配累积曲线

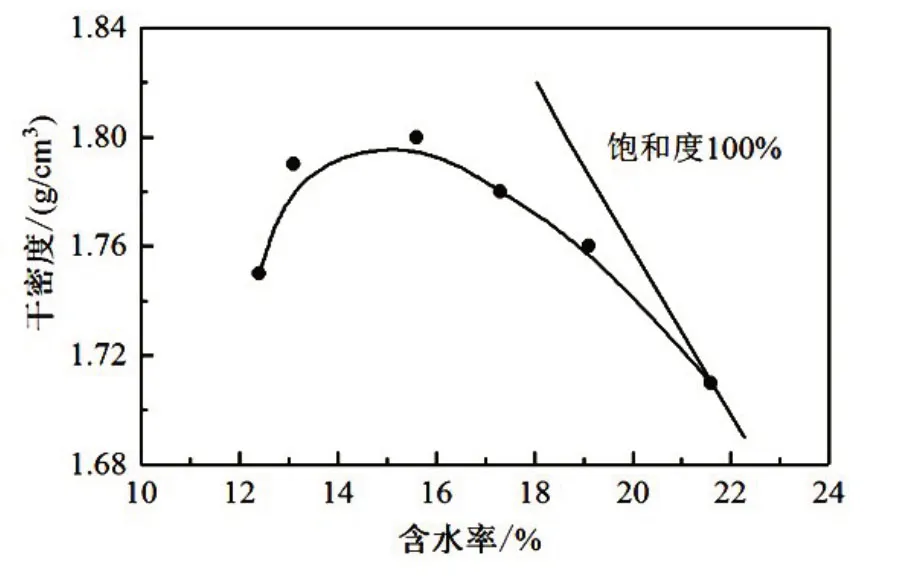
图2 试验黄土的击实曲线

将该土样制成3种干密度分别为1.6、1.7和1.8 g/cm3的压实土样。制样方法为：首先将一定量的原状土样风干、碾碎，平铺于盛土盘中，均匀喷洒水至10%含水率，用保鲜膜密封静置12 h 后搅拌均匀，装入保鲜袋密封置于保湿器48 h，使水分充分分布均匀。接着将定量土倒入提前放入带环刀的制样器中，再用千斤顶压实，即得到特定干密度的环刀样。所用环刀高20 mm，内径61.8 mm。试验制得3种干密度的土样，室内常规试验测得这3种压实土样的基本物理参数如表2。

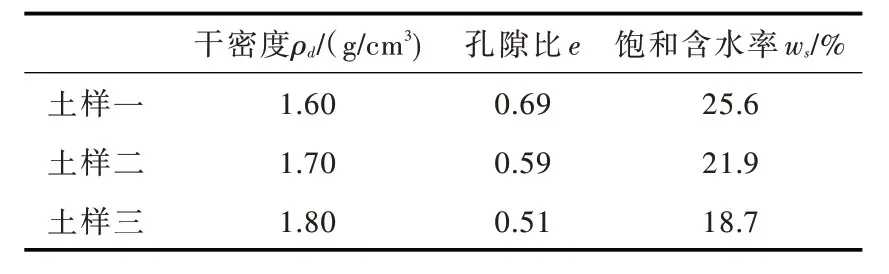
表2 3种压实土样的基本物理参数

3 试验方法

制样完成后，分别对这3种干密度的压实土样进行渗透试验及压汞试验测试其渗透性曲线及孔隙分布曲线。

3.1 渗透试验饱和渗透系数测试采用的是变水头法，所用仪器为TST-55 渗透仪。非饱和渗透系数的测试采用的是李华等[14]提出的基于滤纸的土柱法。该方法的试验装置如图3所示。整个装置包括上方的供水系统和下方的土柱。供水系统是由供水瓶及悬在其上方的马氏瓶组成，马氏瓶向供水瓶提供稳定水头，供水瓶通过底部的混凝土块向土柱提供匀速缓慢的流速。上部装置的给水速率（即土柱的上部入渗速率）影响渗透性曲线的测试结果。如果入渗速率过快，则吸力变化过快，导致数据缺失和离散；而入渗速率过慢，则会延长试验周期，费时费力[18-19]。本试验设定上部装置的给水速率为2 cm3/h 左右，这一速度下既能保证水分不从土柱上方溢出，又能得出较为完整的渗透性曲线。

下方的土柱是由6个带环刀的土样叠置而成，每两个环刀之间夹有一张Whatman No.42 滤纸以测量基质吸力，每个土样上下表面设置普通滤纸以防止中间的滤纸上沾上土。整个装置靠在一个半圆形的有机玻璃柱上，以保持土柱竖直和稳定。

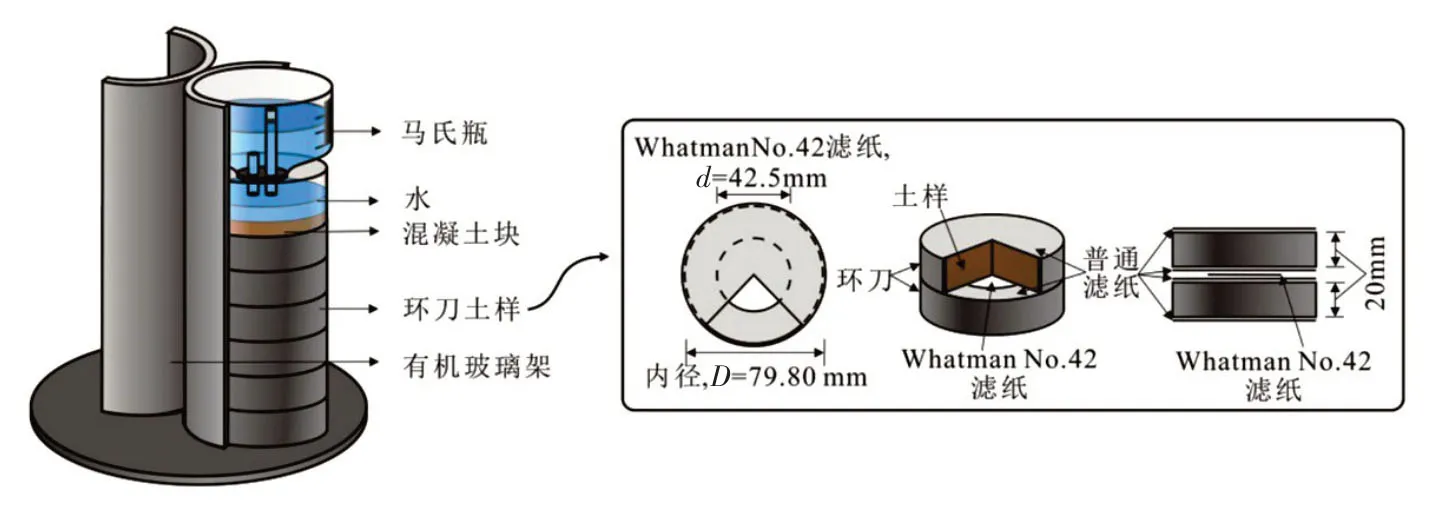
图3 非饱和渗透实验装置

试验时，先提前将6个土样在108 ℃下烘干8 h，5个滤纸108 ℃烘干16 h，用精度0.01 g 的电子天平与精度0.0001 g 的分析天平分别称量土样和滤纸的质量，然后叠置成土柱。在水分下渗过程中，每隔4 h 称量每个土样与滤纸的质量，以换算成土柱的含水率剖面与水头剖面。整个装置封闭在一个有机玻璃筒中，以防止蒸发。环境温度保持在20 ℃。

称得滤纸的质量后，根据事先称得的干滤纸质量计算滤纸的含水率。再根据ASTM 标准提供的Whatman NO.42 滤纸率定方程可以计算出其对应的基质吸力：

式中：ψ为土的基质吸力；wfp为测得的滤纸的含水率。

这两个率定方程分别对应高吸力段和低吸力段两部分。

将这些含水率及基质吸力数据绘成含水率剖面及水头剖面，然后用向后差分法计算水力梯度im，ave：

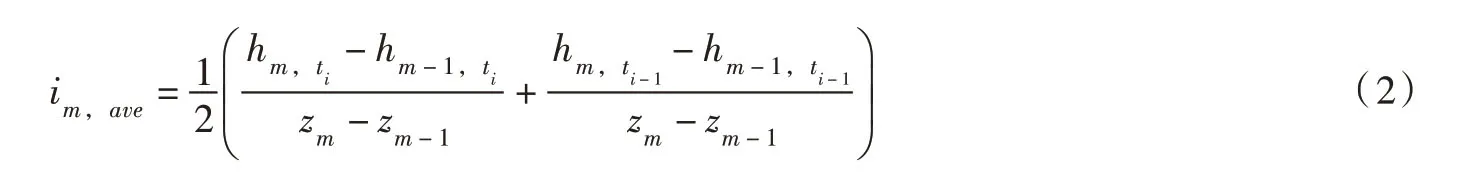
式中：hm，ti-1、hm，ti分别为m计算截面在ti-1和ti时刻的总水头；hm-1，ti-1、hm-1，ti分别为m-1 计算截面在ti-1和ti时刻的总水头；zm、zm-1为m与m-1 截面的位置（距离土柱顶面的距离）。

计算截面m的流量ΔVw等于截面m以下土柱部分的水分增量：

根据达西定律，m截面在计算时间间隔Δt内的渗透系数为：

画出基质吸力与渗透系数的点线图，即非饱和渗透曲线。这一测试方法简单快速，吸力量程可达到1～105kPa，可得到完整的全吸力范围的非饱和渗透曲线。

3.2 压汞试验用压汞试验测试3种土样的孔隙分布曲线。试验过程为将土样削成直径1 cm、高2 cm的圆柱体，冷冻干燥以保证在不改变土壤孔隙的条件下排出水分，然后将土样放入AutoPore IV 9500全自动压汞仪中进行压汞试验，该压汞仪可施加压力0～414 MPa，孔径测量范围0.003～1000 μm。

4 试验结果

变水头饱和渗透系数测试结果见图4，可见3种土样的饱和渗透系数在10-5～10-6m/s之间。随着干密度的增大，即孔隙率的降低，饱和渗透系数以指数趋势减小。将上部给水装置的累计供水量随时间的关系称作流量时程曲线，如图5所示。

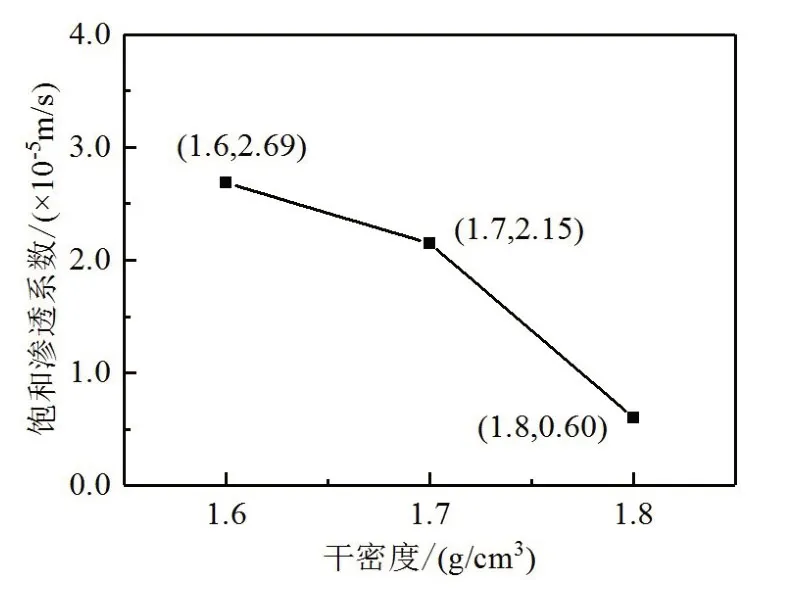
图4 3种压实土样的饱和渗透系数

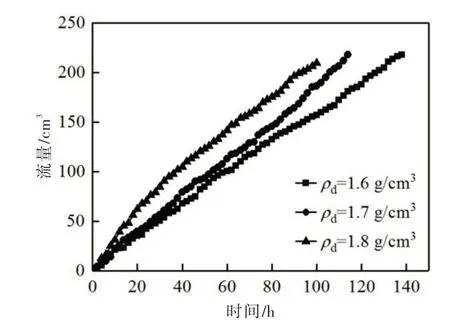
图5 3组实验给水装置的流量时程曲线

图5表明，同一时刻土样的入渗速率总是1.8 g/cm3＞1.7g/cm3＞1.6 g/cm3；而试验的总时间：1.8 g/cm3＜1.7 g/cm3＜1.6 g/cm3。由于本试验得到了大量时间点的测量数据，很难在一张图上画出每个时间点的含水率或基质吸力剖面，因此，将这些数据用时程曲线来表示，时程曲线记录了土柱不同位置z（cm）处含水率或基质吸力随时间变化的过程，z为测量点距离土柱顶面的距离（即式2、式3 中的z），也可以用来计算渗透系数。3种土样的含水率时程曲线及基质吸力时程曲线如图6所示，可以看出：（1）土柱各个位置含水率的增长分三个阶段，第①阶段缓慢增加，第②阶段急速增加，第③阶段缓慢增加，直至各个位置的含水率基本相等而后继续增加，此时整个土柱仍未达到饱和。（2）土柱各个位置的基质吸力的减小也分为相应的三个阶段，即缓慢减小、急速减小、缓慢减小至各个位置基本相等而后继续减小。

用图6数据计算出的渗透性曲线如图7所示，表示为基质吸力与渗透系数的关系。本实验为增湿过程，即基质吸力逐渐减小。基质吸力从105kPa 减小到0.1 kPa，渗透系数从10-14m/s 增加到10-6m/s。可见黄土从干燥到饱和，其渗透系数变化可以产生8个数量级的变化。渗透性曲线的形态从右到左可分为如图7中的a-b-c三段，a、b、c之间存在两个明显的转折点ψt与ψa。a段是从吸力最大点到转折点ψt的曲线，这一阶段在双对数坐标上呈从右到左上升的直线段，渗透系数随着吸力减小呈指数增大，将此段曲线称之为缓升段；b阶段是从转折点ψt到进气值ψa的曲线段，这一阶段随着吸力减小，渗透系数快速增加，在双对数坐标上呈现斜率较大的直线段，渗透系数随吸力减小呈指数增大，将此段曲线称为陡升段；c段是从进气值ψa点到吸力最小点ψ=0.1 kPa，这一阶段随着吸力的减小，渗透系数基本不变，土样饱和，渗透系数为饱和渗透系数，称之为饱和段。另外，干密度越小的土样，a、b两段斜率差异越明显，三段的分异越明显。

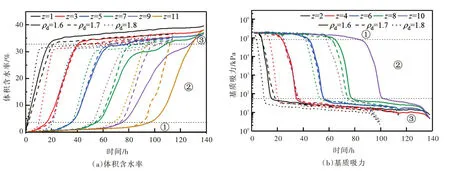
图6 3种土样的含水率与基质吸力时程曲线

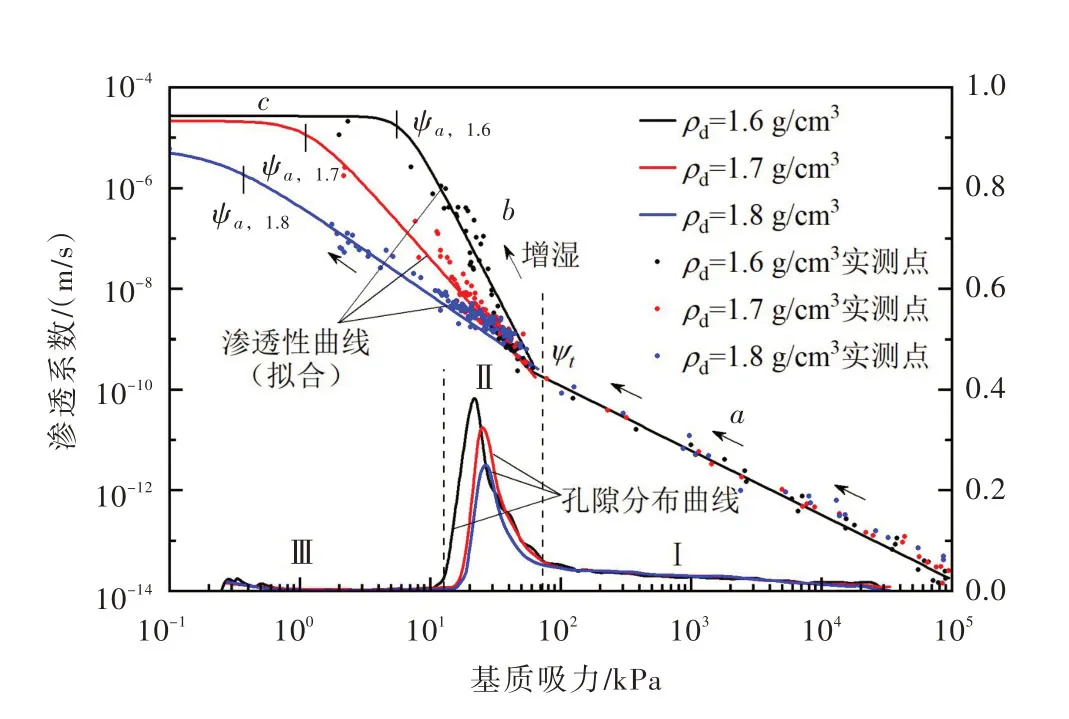
图7 渗透性曲线与孔隙分布的关系

Gardner[1]的双参数模型是描述渗透曲线形式的常见模型，但该模型的曲线只有一个饱和段及一个斜率不变的下降段，适用于颗粒粗且吸力处于进气值附近的土体（Lu 等[20]），如砂土，不足以用来描述存在三个阶段的黄土的渗透性曲线。因此以转折点ψt=60 kPa为界限，将曲线分为低吸力段（ψ≤60 kPa）与高吸力段（ψ≥60 kPa）两部分，用两个不同的函数模型分别拟合高吸力段与低吸力段的渗透性曲线。低吸力段用Gardner[1]的幂函数模型拟合，高吸力部分用简单幂函数拟合。函数表示为：

式中：k为渗透系数；ks为饱和渗透系数；a1、n1为低吸力段的拟合参数；a2、n2为高吸力段的拟合参数。

本试验中3种土样的拟合参数见表3，拟合曲线见图7。

表3 3种土样渗透性曲线的拟合参数

由图7的渗透性曲线可以看出3种不同干密度压实黄土的渗透性曲线具有以下特征：（1）在低吸力段（ψ≤60 kPa），即含水率较大的部分，3种干密度的土样渗透系数差别大。一方面，干密度越小的土样渗透性越大，k1.6＞k1.7＞k1.8，这与饱和渗透系数的规律一致。另一方面，干密度越小，进气值ψa越大，ψa，1.6＞ψa，1.7＞ψa，1.8。（2）高吸力段（ψ≥60 kPa），即含水率较小的部分，3种土样的渗透性曲线基本重合。这说明土样在含水率较小、基质吸力高时，干密度对其渗透性几乎没有影响。

为了解释渗透曲线的这些规律，用压汞试验测得了3种土样的孔隙分布曲线，如图8所示。

Li 等[21]基于雷祥义[22]对黄土孔隙的讨论，总结了现有文献对黄土孔隙的分类，孔径＜2 μm 的为微孔隙，为胶结物孔隙或称作集粒内孔隙；2～8μm 的为小孔隙，8～32 μm为中孔隙，小孔隙和中孔隙都是粒间孔隙，即骨架颗粒之间的孔隙；＞32 μm 的为大孔隙，这部分孔隙包括虫孔、根孔、节理裂隙之类的孔隙。

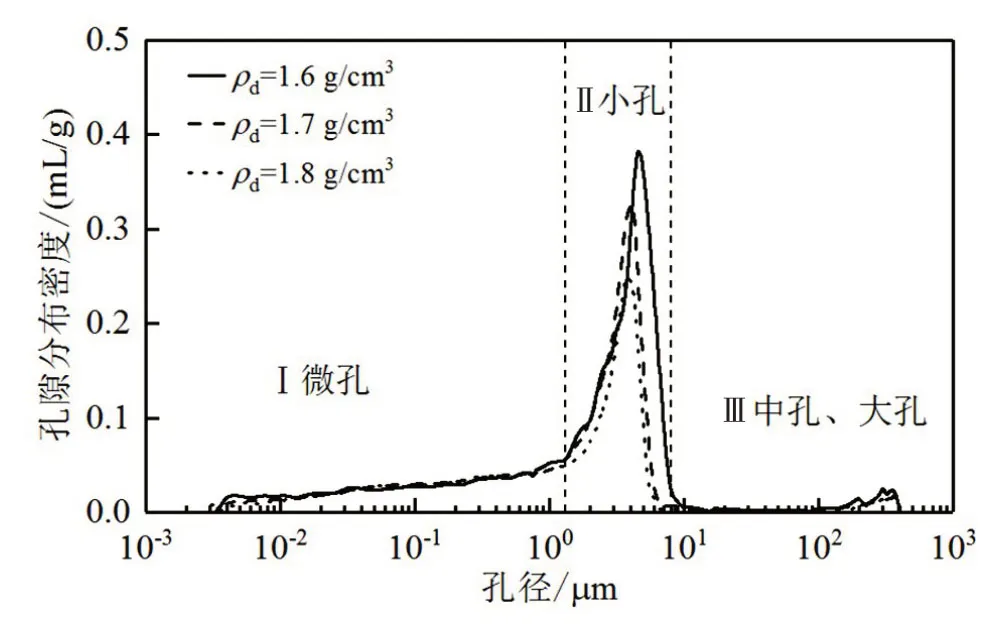
图8 3种压实土样的孔隙分布曲线

本文所测的孔隙分布曲线（图8）分为3个部分，将各部分对应上述孔隙类型，有以下特征：第Ⅰ部分：孔径d＜1.3 μm，对应微孔隙，即集粒内孔隙。3种土样这部分孔隙的数量及分布密度基本一致。第Ⅱ部分：1.3 μm＜d＜8 μm，对应小孔隙。该孔径范围在所有尺寸孔隙中的含量最多，因此也称作黄土中的优势孔隙。第Ⅲ部分：孔径d＞8 μm，对应8＜d＜32 中孔基本没有，只有少量d＞100 μm 的大孔，可能是压实过程中残留的大孔隙。可见本试验中干密度不同的3种压实黄土的孔隙主要区别于孔径1.3 μm＜d＜8 μm 的小孔含量。干密度越大，小孔含量越少，导致土样的总孔隙率减小。

根据杨-拉普拉斯方程，将孔隙分布曲线中的孔径换算为基质吸力：

式中：ua-uw为基质吸力；T为气-水交界面上的表面张力；α为固-液接触角；d为孔隙直径。

据此绘出孔隙分布密度随基质吸力的变化曲线，同时将图8中三部分孔隙对应在曲线上，如图7的孔隙分布曲线。曲线中从右到左随着基质吸力减小分别对应第Ⅰ部分微孔、第Ⅱ部分小孔、第Ⅲ部分中孔和大孔，即基质吸力越小对应越大的孔隙。这是因为基质吸力较大即土壤含水率较小时，这时水分优先进入较小的孔隙；随基质吸力减小，即含水率增大，小孔隙已饱和，水分逐渐进入更大的孔隙。

将孔隙分布曲线与渗透性曲线同时绘制在图7中进行对比。可以看出，孔隙较小时（孔隙分布曲线第Ⅰ部分），渗透系数较小；而当孔隙分布曲线进入峰值段时（第Ⅱ部分），渗透曲线进入陡升段。这是因为第Ⅱ部分孔隙比第Ⅰ部分孔隙尺寸大而且数量多，因此孔隙联通性更好，流动路径更短，渗透系数更大。

图7中，渗透性曲线的高吸力段（ψ ＞ψt）对应孔隙分布曲线的第Ⅰ部分微孔，低吸力段（ψ＜ψt）对应第Ⅱ部分小孔和第Ⅲ部分中孔、大孔。对比图7中不同干密度土的渗透性曲线与孔隙分布曲线，结果发现：在高吸力段（ψ ＞ψt）：3种土样孔隙分布曲线完全重合，即第Ⅰ部分微孔的各级孔隙含量相同，因此渗流路径的截面积也相同，渗透系数也相等，渗透曲线基本重合。也就是说，干密度不影响压实黄土的微孔数量，也不影响其对应的高吸力部分渗透系数；在低吸力段（ψ＜ψt）：不同土样的孔隙分布曲线与渗透性曲线均不再重合。此时由于吸力的减小，含水率增大，微孔隙已饱和，水分开始进入孔径更大的小孔（Ⅱ）。根据孔隙分布曲线，不同干密度的土这部分孔隙密度差异明显，因此渗透系数亦不再相同；干密度越小的孔隙，这部分孔隙含量越多，则渗流路径的截面积越大，因此渗透系数更大。这就解释了低吸力段渗透系数k1.6＞k1.7＞k1.8。渗透性越大，增湿过程中越快排出土中所有气体，达到饱和，因此进气值ψa，1.6＞ψa，1.7＞ψa，1.8。

第Ⅲ段中孔和大孔含量很少，其对土样的渗透性的影响甚微。饱和渗透系数只与孔隙度有关，孔隙度越大，饱和渗透系数越大。

本文的研究对象为延安地区L6压实黄土的渗透性曲线与孔隙特征，L6为离石黄土层。理论上由于黄土的孔隙结构相似，本文所述渗透性曲线的特征对于所有黄土均有参考价值，但对于黏粒含量较多且孔隙分布较均匀的古土壤，其规律或有不同。对于其他地区、深度的黄土其渗透性曲线的规律还需进一步研究。

5 结论

本文实测了3种不同干密度的压实黄土的渗透系数曲线和孔隙分布曲线，得出了不同干密度压实黄土的以下渗透性特征：（1）随基质吸力减小，压实黄土的渗透性曲线形态有三段，缓升段，陡升段和饱和段。这三个阶段的临界点分别是曲线斜率改变的拐点ψt和进气值ψa点，本试验中ψt=60 kPa。（2）不同干密度的压实黄土其渗透系数的差异主要在低吸力段，即渗透系数陡升段和饱和段，干密度越小，渗透系数越大；在高吸力段，即渗透系数缓升段，渗透系数基本相同。（3）土的渗透系数大小与其孔隙特征密切相关。对于不同干密度黄土，微孔数量基本相同，因此渗透系数也基本相同；孔径为1.3 μm ＜d＜8 μm 的小孔，数量差异明显，因此渗透系数也不同，小孔越多，相应的渗透系数越大；中孔、大孔含量很少，其对土样的渗透性的影响甚微。