基于断裂力学的起重机结构概率-非概率疲劳可靠性分析*

李建明, 丁 谦

(1.山西梅园永兴煤业有限公司，山西 太原 030024; 2.太原科技大学 机械工程学院，山西 太原 030024)

0 引 言

起重机械是现代工业生产中用于大型物料搬运的重要设备。同样在煤矿生产制造中也发挥着至关重要的作用。起重机工作时主梁承受着起升货物带来的交变载荷，随着使用年限的增加，其金属结构内部由于焊接及冶炼所造成的夹渣、气孔等微小损伤将不断积累，当损伤达到临界值的瞬间，会发生疲劳失效，给人们带来巨大伤害。因此，对起重机主梁进行疲劳可靠性分析具有重大意义。

在工程可靠性分析中常使用概率模型，这种随机概率可靠性分析方法的发展已非常成熟，并且在机械金属结构、桥梁、建筑等各个领域已经取得了一些成就。但概率模型也有一定的局限性，即需要知道变量的分布规律，然而在实际工程中有些不确定性变量的精确统计数据难以得到，在计算时往往都是通过经验假设，简化得到其分布函数，这可能使结果出现较大的误差。为描述这些无法获得分布规律的不确定性变量，出现了非概率可靠性分析方法。1994年Ben-Haim提出了基于凸集模型的非概率可靠性概念，随后这一理论在结构可靠性分析中的应用得到了广泛研究。针对某些只知道取值范围的不确定变量，1995年基于区间模型的非概率可靠性分析方法又被Ben-Haim和Elishakoff提出，该方法将不确定性参数定义为区间变量，通过区间四则运算进行可靠性分析。由于无法获知不确定参数的概率分布，杨淑伟等[9]等采用凸模型非概率方法对起重机臂架结构进行了可靠性分析。崔智勇等[10]基于微粒子群算法的区间模型的非概率可靠性分析方法计算了悬臂梁的可靠性指标。近年来，国内郭书祥[8]又提出了一种概率-非概率混合可靠性分析方法。目前，在起重机金属结构疲劳可靠性分析中主要采用概率可靠性分析方法。例如：徐格宁等[4]将初始裂纹作为随机变量应用概率的方法，对起重机焊接箱型梁疲劳寿命的可靠度进行了计算。史朝阳等[3]采用概率模型对桥式起重机主梁进行了疲劳可靠性分析。杜永恩等[5]采用基于区间非概率的方法计算了飞机机翼主梁螺栓孔的疲劳可靠性指标。

由于在起重机金属结构的疲劳可靠性分析中，不仅存在着能用概率分布描述的随机变量，还存在着难以用概率描述其分布类型的区间变量。鉴于此，笔者将概率和非概率分析理论相结合，并首次用于起重机主梁结构疲劳可靠性分析。即通过运用断裂力学法对起重机箱型主梁疲劳剩余扩展寿命进行估算，将初始裂纹尺寸a0、应力幅σ以及材料参数m作为随机变量，将临界裂纹尺寸ac、材料参数C以及形状参数F作为区间变量，根据Paris公式，建立概率—非概率疲劳可靠性分析的混合模型，并给出了求解疲劳混合概率可靠度的计算方法。经数值案例和起重机金属结构的工程案例计算表明，与传统的概率可靠性分析相比,这种分析方法更符合实际也更安全。

1 概率可靠性分析方法

可靠性分析的概率模型中，可靠度Pr可表示如下：

Pr=P(g(X)>0)

(1)

式中:P(.)表示概率;g(X)为功能函数，g(X)=0为极限状态方程，设向量X={x1,x2,…,xm}为与结构失效相关的随机变量，且相互独立，m为变量个数。一般通过一阶二次矩法或MonteCarlo方法求解。文中采用MonteCarlo方法求解。

2 基于区间分析的非概率可靠性

在区间分析的非概率可靠性模型中，设向量Y={y1,y2,…,yn}为与结构功能相关的区间变量集合，并且区间变量之间相互独立。于是可得功能函数如下：

M=g(Y)=g(y1,y2,...yn)

(2)

(3)

用标准化区间变量表示变量yi，可得如下功能函数:

g(Y)=g(y1,y2,…yn)=G(δ1,δ2,…δn)

(4)

式中:(δ1,δ2,…,δn)是标准化区间变量，通过非概率可靠性优化法，可得其下上限:

(5)

(6)

Mu,Ml分别为功能函数上下界，那么非概率可靠性指标可得：

(7)

3 概率-非概率混合可靠性分析

当影响结构功能的不确定性变量中，随机变量和区间变量同时存在时，那么其功能函数可以表示为：

M=g(X,Y)=g(x1,...,xm,y1,...,yn)

(8)

其中，X={x1,...,xm}为随机变量向量，Y={y1,...,yn}为区间变量向量。设向量X取常值，那么式中仅有区间变量，为非概率可靠性问题。当向量Y为常值时，式中仅有随机变量，为概率可靠性问题。基于这一思想，首先将随机变量X视为常值向量，应用非概率优化法进行可靠性分析，那么非概率可靠性指标η为：

(9)

M(2)=η(X)-1=0

(10)

上式只存在随机变量,可以通过概率可靠性分析方法求解。于是结构的可靠概率可表示为：

Pr=P(M(2)>0)=P(η(X)-1>0)

(11)

此时不可靠失效概率为：

Pf=1-P(η(X)-1>0)

(12)

4 基于断裂力学理论疲劳寿命估算及其参数的分析

4.1 疲劳扩展速率da/dN

根据断裂力学理论可以得到疲劳裂纹扩展速率da/dN与应力强度因子幅值ΔK之间的关系，如图1所示，可分为3个阶段。

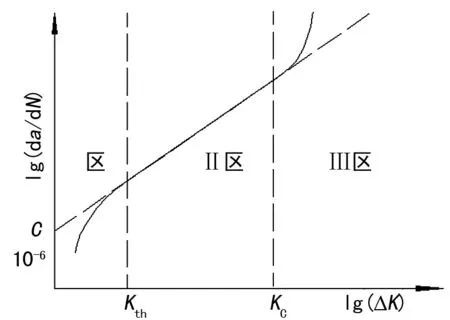
图1 双对数曲线

第Ⅰ阶段:这一阶段ΔK≤ΔKth，此时的应力强度因子幅值ΔK小于裂纹扩展门槛值ΔKth，疲劳裂纹不会发生扩展，称为裂纹不扩展阶段。

第Ⅱ阶段：这一阶段ΔKth<ΔK≤ΔKc，ΔKc裂纹扩展临界值，此时为裂纹稳定扩展阶段。这一阶段是疲劳寿命主要组成部分。文中采用Paris[2,4]公式来表示裂纹扩展率如下:

(13)

式中：a是裂纹长度;N是应力循环次数;da/dN是裂纹扩展速率;C,m是与材料、构件形状等有关的系数;ΔK是应力强度因子幅值，表示如下：

(14)

式中：F是修正系数;σ是应力幅值。

第Ⅲ阶段：这一阶段ΔK>ΔKc临界值，是裂纹迅速扩展阶段，称之为失稳扩展。这一阶段寿命很短，计算时根据实际情况可以不予考虑。

4.2 起重机主梁疲劳扩展寿命模型

起重机箱型主梁由于生产制造、材料缺陷以及焊接缺陷等原因，主梁金属结构内部存在许多的疲劳源，从而使得起重机箱型主梁的形成寿命较短，有时甚至没有萌生寿命。所以，起重机箱型主梁的疲劳寿命主要取决于稳定扩展阶段，由于Paris公式形式简单，应用广泛，最关键是它对第Ⅱ阶段的适用性较好，因此本文采用Paris公式来表示起机箱型主梁的裂纹扩展率。将公式(14)代入式(13),通过积分后可得起重机主梁的疲劳寿命N,如下式：

(15)

4.3 确定主梁疲劳危险位置

通过疲劳试验和起重机实际检测数据，得出发生疲劳断裂的两个位置:一是腹板-下盖板纵向受拉翼缘连续贴角焊缝上;二是横隔板-腹板连接焊缝底部的焊趾处。

4.4 影响裂纹扩展速率的不确定性参数的选取

起重机金属结构的几何参数和材料属性等参数会受到生产制造、工作环境以及测量误差等的影响，所以这些参数是具有不确定性的，从而使疲劳分析结果出现较大的差异。因此，要全面考虑参数的不确定性。下面将对影响起重机箱型主梁疲劳寿命参数进行分析与取值。

Paris公式中的裂纹扩展参数C，m与材料属性和构件的几何形状有关，可通过疲劳试验得到，许多学者对此进行了研究[2,4]。由工作环境、生产制造以及测量误差等的影响，C和m应当是不确定性参数。对于起重机焊接箱型梁，文中取C的均值uc=2.61×10-13，变异系数δc=0.1～0.3之间，从最不利角度出发，取δc=0.3[7]，则可得区间变量C=[1.827,3.393]×10-13。根据文献[3]，m服从正态分布，并可取m～N(3,0.032)。

由于起重机箱型主梁生产完成时就会因为材料缺陷、焊接缺陷等因素就已经形成初始裂纹，因此，a0选为常数不合理。根据文献[3]文中拟将a0取为服从对数正态分布的随机变量lga0～N(0.5,0.52)。根据疲劳试验数据,起重机结构裂纹临界长度ac值范围在80～120 mm[2,4,6]，文中取其为区间变量ac∈[80,120]mm。

形状参数F，是疲劳裂纹尺寸与板宽等的函数，取值通常跟板宽、应力集中等因素的作用有关，无法用统一的公式来表示，属于一个不确定性参数。根据文献[7]将形状参数取为区间变量F=[0.95,1.05]。

5 桥式起重机箱型主梁混合可靠性分析模型

以起重机箱型主梁疲劳寿命安全余量作为功能函数，得极限状态方程如下:

M=N-ND≥0

(16)

式中:M为功能函数;N为应力循环次数，可通过式(15)获得;ND为设计寿命。

根据上节对影响起重机箱型主梁疲劳寿命的不确定性参数的分析，可知，功能函数中既存在随机变量a0、σ、m，又存在区间变量C、F、ac，因此功能函数可表示为如下混合不确定性形式：

M=g(a0,σ,m,CI,FI,acI)=0

(17)

通过文中第3节所述的混合可靠性分析方法即可求解。

6 工程应用

文中通过文献[1]的算例来对36TU型集装箱门式起重机主梁进行概率-非概率混合可靠性分析。基于Paris公式的疲劳估算，其相应的各不确定参数a0、σ、m，C、F、ac的取值如上所述。

载荷通过现场实测,以周(7天)为单位统计载荷数据,再应用雨流计数法得到载荷谱,最后通过有限元分析得到危险点的应力谱。根据应力幅σi与最大应力幅值σmax的比值分为8级。相应的应力幅值和其频率如表1所列。图2是各级应力幅出现的概率图。

表1 一周内主梁危险点处的应力幅谱

图2 各级应力幅出现的概率

由图2所示的概率图可见应力幅可能服从正态分布，为此基于Matlab软件对表中的数据进行正态判别与拟合，得出σ～N(71.4445，25.73932)。应用本文的混合可靠性分析方法对该门机主梁进行疲劳可靠性分析。

同样将区间变量根据上述方法假设为随机变量，可以得到：

C～N(2.61×10-13,(2.61×10-14)2)

F～N(1,(1.67×10-2)2)

ac～N(100,6.672)

在通过概率可靠性方法求解，将混合可靠性和概率可靠性分析计算出的可靠度结果列于表2。

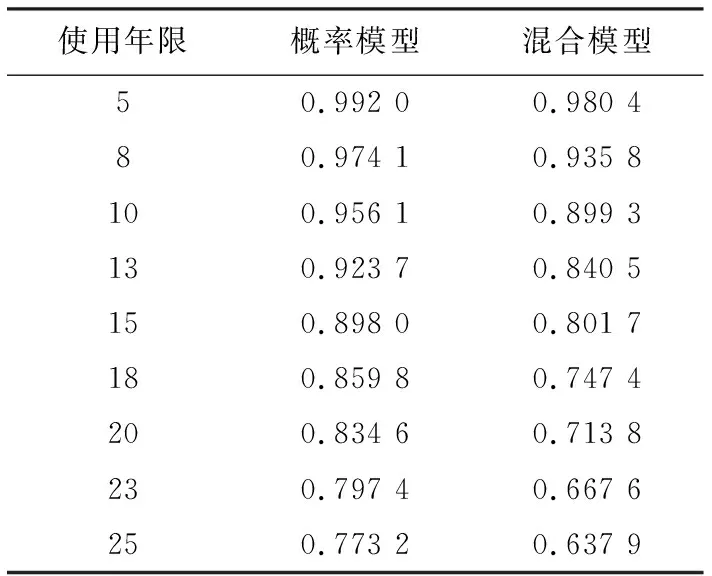
表2 36TU门机可靠性分析结果

为了便于对36TU门机不同可靠性模型分析结果的比较，将表4的可靠度结果列于图3。

图3 36TU门机主梁可靠度变化曲线

从图3可以发现混合疲劳可靠性分析模型得出可靠度小于概率模型，这说明当影响疲劳寿命的不确定性参数没有确切的分布规律时，采用随机变量进行处理来进行疲劳可靠性分析，忽略了真实数据的分散性，而使所得结果产生一定的差异。而用区间变量对参数的不确定性进行定量化比用随机变量来描述更精确。因此混合可靠性方法考虑到的影响疲劳失效因素更全面，更符合实际，也更能保障起重机的安全使用。

7 结 论

(1) 针对起重机金属结构的不确定性变量既存在随机变量又存在区间变量的问题, 首次提出用概率—非概率混合可靠性分析方法对起重机疲劳进行分析，根据Paris公式构建了疲劳寿命安全余量混合可靠性分析模型，并利用本文所述概率—非概率混合可靠性分析方法对桥式起重机箱形主梁进行了疲劳可靠性分析。

(2) 这种疲劳混合可靠性模型,根据结构疲劳失效准则建立一级功能方程, 在其中的随机变量取其实现值的条件下, 进行非概率可靠性分析;再根据非概率可靠度指标大于1结构可靠的这一理论建立了二级功能方程,并进行随机可靠性分析。通过实例验证与传统的概率可靠性分析相比,这种分析方法更复合实际也更安全。

(3) 通过文中分析为起重机疲劳可靠性分析提供了一条新的思路，可以看出，混合可靠性分析方法在起重机金属结构疲劳可靠性分析中有比较好的适用性。但是目前这种混合可靠性分析方法还不太成熟，可以通过对这种混合可靠性方法进行改进后再与起重机金属结构相结合做进一步的研究。