中低速磁浮道岔车岔耦合振动分析

（西南交通大学 机械工程学院，成都 610031）

0 引言

磁浮列车具有速度快，无噪音，环保等优点，是21世纪理想的超级快车，世界各国都十分重视发展磁浮列车。目前，国内外学者对道岔进行了一系列研究。靖仕元[1]通过对长沙磁浮工程道岔梁安装阻尼器进行试验，测量了阻尼器对磁浮道岔减振情况。龚朴[2]对五转向架磁浮车辆的结构及行驶过弯进行了分析，得到了中低速磁浮车辆运行需求。陈越龙[3]将可靠性技术应用于磁浮道岔中。Jong-Boo Han[4]进行了车辆在磁浮道岔上悬浮稳定性研究。以上论文主要研究了磁浮列车及道岔的设计，实验中的表现，可靠性的研究，而很少对磁浮道岔进行耦合振动分析。磁浮道岔是磁浮列车行驶过程中的薄弱环节，道岔梁的主要材料是Q235，因为这种钢结构没有阻尼，在轨道不平顺及磁浮列车的悬浮电磁铁及空气弹簧的振动影响下，车辆-道岔容易发生耦合振动，造成打轨或更严重事故。因此对磁浮道岔进行耦合振动分析具有重要意义。

磁浮道岔的稳定性对磁浮车辆行驶过程中的人员安全至关重要，道岔的刚度和强度必须满足要求，道岔自身的结构特性也应能承受车辆行驶引起的振动变形。本文以某26.5m中低速磁浮道岔为研究对象，分析道岔的振动情况。

磁浮道岔结构部分主要由主动梁、第一从动梁、第二从动梁、固定端垛梁、活动端垛梁、梁间竖向支承滑动装置等部分组成[5,6]，如图1所示。

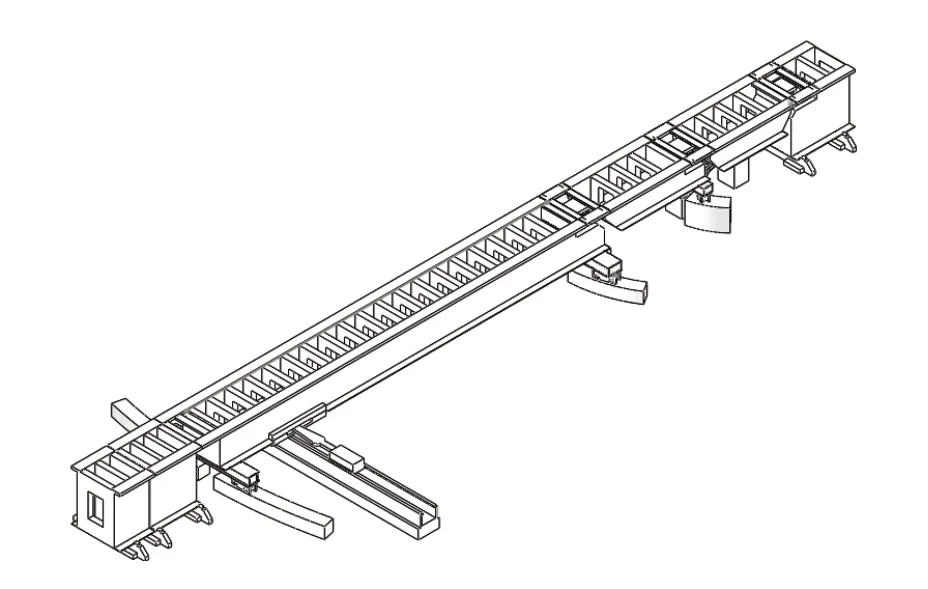
图1 磁浮道岔的结构模型

1 磁浮道岔纵向等效刚度分析

道岔梁由三段梁和三个连接板构成。磁浮列车在磁浮道岔上行驶时，依次经过连接板三，第二从动梁，连接板二，第一从动梁，连接板一，主动梁。

磁浮列车在磁浮道岔上行驶时，悬浮架上的悬浮电磁铁对道岔梁产生均匀压力。磁浮列车行驶至每节道岔梁边界附近时，由于其下有支座支撑，道岔梁变形较小；当磁浮列车行驶至道岔梁正中时离支座最远，所以此时其竖向变形最大。设道岔梁竖直方向上的变形与列车过岔行驶距离的函数关系为x（l）。

因为磁浮列车行驶时，道岔梁的载荷是变化的，为了得到磁浮道岔纵向等效刚度，将整个道岔梁分为6节，并分别对每节梁上选取30个等距的应变测量点。然后使用有限元软件ANSYS对磁浮道岔进行静力学仿真计算，计算后分别记录每节上所有测量点应变x的数值，为分段拟合做准备。

对于第一节道岔梁，因为不知道x1（l）的具体形式，而知道一些节点l1，l2，…，l30处对应的函数值x1（l1），x1（l2），…，x1（l30），进而知道了x1（l）对应曲线的大致趋势[7]。假设函数系所产生的空间中的函数曲线较适合未知函数x1（l），现要从Φ 中找到一个最适合x1（l）的函数即在最小二乘曲线拟合中的度量指标——向量的2范数达到最小[7]，即求解

因为当阶数n过大时，会产生振荡现象影响精度，阶数过小会导致拟合曲线与原曲线误差偏大，所以选择4阶多项式拟合。

因为道岔梁在竖直方向上的变形为x（l），列车重量P=320000N，则由P=kx得到刚度与列车过岔行驶距离的函数关系为k（l），即为等效刚度。中低速磁浮道岔等效刚度k（l）图像如图2所示。

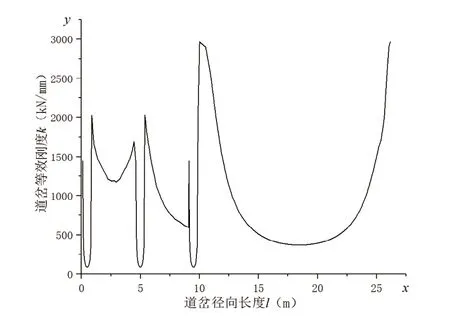
图2 磁浮道岔等效刚度曲线

2 车岔无阻尼振动特性

2.1 周期性轨道不平顺激励

轨道不平顺是指轨道的几何形状、尺寸和空间位置相对其正常状态的偏差，常见轨道不平顺的波长范围为0.01～120m[8,9]。考虑到梁的收缩和蠕变以及温差引起的上（下）拱，可以认为其不平顺近似于正弦曲线，即：

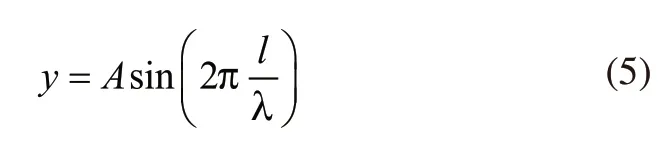
式中，A为不平顺幅值；

λ为不平顺波长；

L为从初始点到计算点的距离；

Y为不平顺高度。

磁浮列车系统对轨道功能区提出了严格的制造精度要求，对3个功能面制造安装精度要求基本上都在1mm以下，故正弦不平顺幅值可取为1mm，按列车匀速行驶时进行分析，则从初始点到计算点的距离l可表示为磁浮列车行驶速度v和行驶时间t的乘积。

假定磁浮列车轨道之间的距离恒定，则不平顺高度y对时间t求二阶导得到磁浮列车在垂向的加速a（t），再乘上磁浮列车自身总质量m=32000kg，即得到列车施加到轨道上的力f关于时间t的函数：

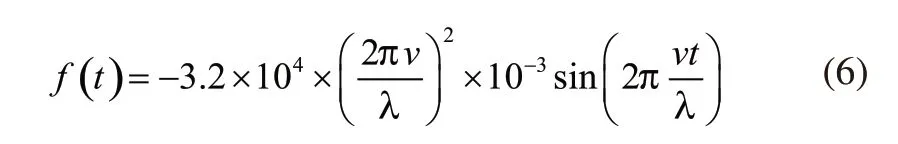
本文取轨道不平顺波长λ=3m，将模拟的不同速度v代入式(6)即可得到f（t）表达式。

2.2 无阻尼道岔梁车岔耦合振动分析

因为道岔梁是钢结构，则道岔梁在振动过程中没有阻尼作用，磁浮道岔耦合振动的动力学方程如式(7)所示：

式中x为道岔梁应变。

为了简化计算，采用时域分析。由于中低速磁浮列车通过道岔的运营时速不高于80km/h[10]，则在仿真中取列车运行速度为80km/h，60km/h，40km/h，由l=vt可得f（t）随磁浮列车行驶距离l的函数表达式f（l）。然后使用MATLAB进行无阻尼磁浮道岔耦合振动仿真分析，其动力学分析原理图如图3所示。

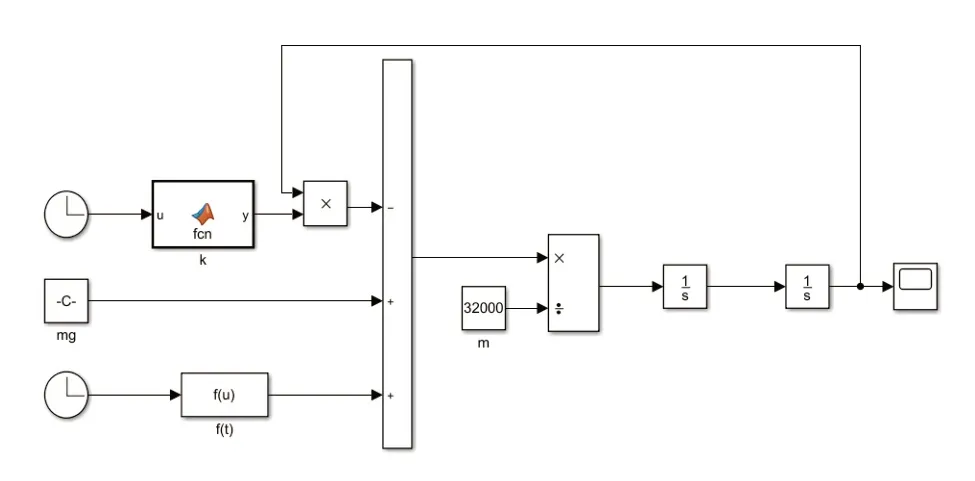
图3 列车过岔时无阻尼道岔梁振动分析原理图

动力学分析后得到在磁浮列车以速度为80km/h，60km/h，40km/h通过中低速磁浮道岔时，道岔梁最大应变随时间变化的函数图像，如图4所示。

图4 列车过岔时无阻尼道岔梁应变曲线

图4为无阻尼时，道岔梁最大应变的变化曲线，其中曲线1、2、3分别为磁浮列车速度为80km/h，60km/h，40km/h时的道岔梁最大应变曲线。

在磁浮道岔的耦合振动分析过程中，当列车的位置随时间改变时，道岔梁上各点的垂向位移也在随时间变化。由列车过岔时无阻尼道岔梁应变图可以看出振动的曲线由多种振动叠加而成，包括轨道不平顺激励的振动，道岔梁不同位置时的刚度不同而造成道岔梁的反力变化而引起的振动及振动的叠加。在通过26.5m道岔过程中，列车以80km/h，60km/h，40km/h速度通过道岔时道岔梁的最大应变分别为1.91mm，1.59mm，1.23mm。由此可知在磁浮列车通过道岔时速度越快，道岔梁的最大应变越大。因为一般情况下列车过岔的速度不超过80km/h[10]，则道岔梁的最大应变不超过1.91mm，相对于磁浮道岔整体尺寸而言较小，小于危险值，但道岔的变形将影响悬浮电磁铁的控制系统，从而增大车体的振动，影响车体平稳性，因此减少道岔振动必不可少。

3 有阻尼车岔耦合系统动力学分析

因为道岔梁是没有阻尼的钢结构弹性体，则振动容易发生累积。为了减少振动，采用对道岔梁并联阻尼器的办法减少磁浮道岔的振动[11]。

粘性阻尼力Fd与振体速度大小相同方向相反，大小为。其中c为粘阻系数，它取决于物体的形状、尺寸和润滑等物理性质。磁浮道岔耦合振动的动力学方程如式(8)所示。

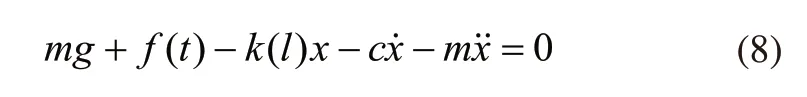
然后对磁浮道岔梁并联阻尼器进行分析，选择比较合适的粘阻系数c。然后采用时域分析，使用MATLAB进行磁浮道岔耦合振动仿真分析，其动力学分析原理图如图5所示。

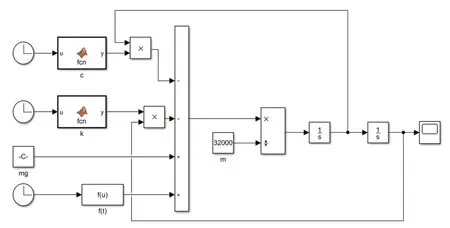
图5 列车过岔时有阻尼道岔梁振动分析原理图

动力学分析后得到中低速磁浮道岔在并联阻尼后，当磁浮列车通过道岔时，道岔梁最大应变随时间变化的函数图像，如图6所示。

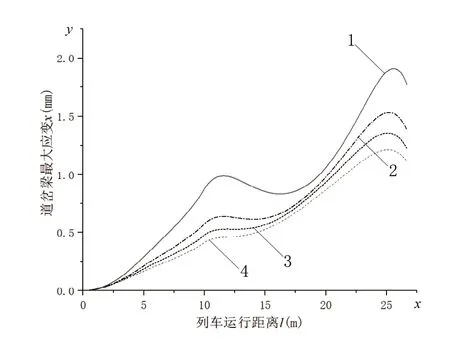
图6 列车过岔时有阻尼道岔梁应变曲线

图6为并联阻尼器后磁浮列车以速度80km/h通过道岔时，道岔梁最大应变的变化曲线。其中曲线1、2、3、4分别表示并联阻尼的粘阻系数分别为c=0N.s/m、c=1×105N.s/m、c=2×105N.s/m、c=3×105N.s/m时的道岔梁最大应变曲线。

在磁浮道岔的耦合振动分析过程中，当列车的位置随时间改变时，道岔梁上各点的垂向位移也在随时间变化。由列车过岔时道岔梁应变图可以看出振动的曲线由多种振动叠加而成，包括轨道不平顺激励的振动，道岔梁不同位置时的刚度不同而造成道岔梁的反力变化而引起的振动及叠加的振动。在磁浮列车以速度80km/h通过26.5m道岔过程中，并联阻尼的粘阻系数分别为c=0N.s/m、c=1×105N.s/m、c=2×105N.s/m、c=3×105N.s/m，此时道岔梁的最大应变分别为1.91mm，1.53mm，1.35mm，1.22mm。由于道岔梁临界阻尼很大，实际情况都是欠阻尼状态，所以在并联阻尼器后，道岔梁最大应变有明显减小，并联的阻尼越大道岔梁振动越小。在并联c=3×105N.s/m阻尼后，列车过岔时道岔梁最大应变从无阻尼的1.91mm减小到了1.22mm，不仅小于危险值，满足结构安全要求，而且道岔梁更小的应变可以减少车身振动，大大提高乘客的舒适度，安全余量更大，安全系数也更高。

4 结语

1）基于中低速磁浮道岔的承载结构特征，本文基于最小二乘曲线回归方法，通过计算道岔梁纵向多点应变建立道岔梁纵向等效刚度曲线，并采用分段函数拟合，可以提高拟合精度，然后采用建立动力学微分方程的方法建立车岔耦合振动模型，并采用MATLAB进行仿真。

2）对中低速磁浮道岔进行耦合振动分析，得到列车以80km/h，60km/h，40km/h速度通过道岔时无阻尼道岔梁的最大应变分别为1.91mm，1.59mm，1.23mm，相对于磁浮道岔整体尺寸而言较小，小于危险值。但道岔的变形将影响悬浮电磁铁的控制系统，从而增大车体的振动，影响车体平稳性。

3）对中低速磁浮道岔并联阻尼器，并建立并联阻尼器后新的动力学方程，使用同样的方法进行动力学仿真，得到列车过岔时有阻尼道岔梁应变曲线图。由图6可知，在并联阻尼器后，道岔梁最大应变有明显减小，在并联c=3×105N.s/m阻尼后，列车过岔时道岔梁最大应变从1.91mm减小到了1.22mm。道岔梁更小的应变可以减少车身振动，大大提高乘客的舒适度。同时安全余量更大，安全系数也更高。