伪标签邻域粗糙集下的属性约简加速策略
饶先胜,宋晶晶,2+,杨习贝,于化龙,王平心
(1.江苏科技大学 计算机学院,江苏 镇江 212003;2.闽南师范大学 数据科学与智能应用福建省 高校重点实验室,福建 漳州 363000;3.江苏科技大学 理学院,江苏 镇江 212003)
0 引 言
粗糙集理论[1]是由Pawlak教授提出的用于数据分析与处理的数学工具。近年来,粗糙集理论在数据挖掘[2]、模式识别[3]、机器学习[4-6]等领域都得到了实际的应用。为提高Pawlak粗糙集的适用性,Hu等提出了邻域粗糙集[7,8],且得到了国内外学者的广泛关注[9-12]。值得注意的是在邻域粗糙集中,所考虑的半径对所得邻域关系的分辨能力具有重要影响,过大的半径会使邻域关系的分辨能力较差。因此,为提高邻域关系的分辨能力,Yang等[13]通过将伪标签策略引入到邻域和邻域关系的构造过程中,提出了伪标签邻域粗糙集。
属性约简[14-17]作为粗糙集理论中备受关注的问题之一,已经得到众多学者的重视。目前,有关约简求解的方法主要有:穷举法[18,19]和基于适应度函数的启发式方法[14]。尽管穷举法可用于求解所有的约简,但过于复杂和耗时。这也是基于适应度函数的启发式方法受到广泛关注的原因。
基于伪标签邻域粗糙集的属性约简问题,可以使用启发式方法来进行求解。但值得注意的是,在不同的半径下进行属性约简时,往往会得到不同的约简结果,而对于不同约简结果,其意义或泛化性能也不尽相同。因此,在多个半径下进行属性约简,有助于观测约简性能的变化趋势和寻找具有较好泛化性能的约简结果。为降低求解伪标签邻域粗糙集中一组半径下约简的时间消耗,本文在现有的启发式算法基础之上,通过考虑在属性约简过程中减少属性的遍历规模,来设计加速策略,以期加快属性选择的过程。
1 基础知识
1.1 伪标签邻域粗糙集
在邻域粗糙集中,邻域决策系统可表示为3元组NDS=
给定一个邻域决策系统NDS,则U/INDd={X1,X2,…,Xp} 为决策属性d在论域上诱导出的划分,其中INDd是关于决策属性d的等价关系,即有INDd={(x,y)∈U×U∶d(x)=d(y)}。∀Xq∈U/INDd,Xq表示具有相同标签样本组成的第q个决策类。
定义1[7]给定一个邻域决策系统NDS,∀B⊆A,则任意样本x∈U关于B的邻域为
δB(x)={y∈U∶ΔB(x,y)≤σ}
(1)
其中,ΔB(x,y) 表示由条件属性集合B计算得到的样本x和样本y之间的距离,σ为半径。
在本文中,采用欧式距离进行计算ΔB(x,y)。此外,论域上关于B的一个邻域关系可以表示为δB={(x,y)∈U×U∶ΔB(x,y)≤σ}。
由定义1可以看出,给定一个半径可以得到论域中任意样本的邻域和论域上的一个邻域关系。但值得注意的是,当给定的半径过大时,两个相似性程度较低的不同类别样本仍可能具有邻域关系,因而会导致在论域上得到的邻域关系的分辨能力较差。因此,Yang等[13]在邻域和邻域关系的构造过程中添加伪标签约束,提出了伪标签邻域粗糙集。
定义2[13]给定一个伪标签邻域决策系统NDSPL,∀B⊆A,则任意样本x∈U关于B的伪标签邻域为
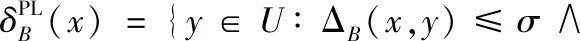
(2)

定义3[13]给定一个伪标签邻域决策系统NDSPL,∀B⊆A,则决策属性d关于条件属性集合B的伪标签邻域下近似和上近似分别为
(3)
(4)
其中,Xq∈U/INDd,且
(5)
(6)
定义4[13]给定一个伪标签邻域决策系统NDSPL,∀B⊆A,则决策属性d关于条件属性集合B的伪标签近似质量为
(7)
其中,|X| 表示集合X的基数。
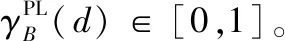
1.2 属性约简
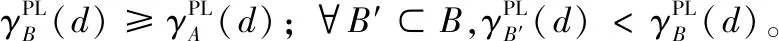
定义5表明A的一个伪标签近似质量约简是能够使得该决策系统的伪标签近似质量不会降低的最小属性子集。因此,根据定义5中的属性约简定义和伪标签近似质量,可以进一步设计如下用于评估候选属性的重要度函数。
定义6 给定一个伪标签邻域决策系统NDSPL,∀B⊆A,则∀a∈A-B,a相对于B关于伪标签近似质量的重要度为
(8)
在定义6中,SigPL是根据伪标签近似质量来评估候选属性重要度的函数。∀a∈A-B,若SigPL(a,B,d) 的值越大,则属性a对提高伪标签近似质量作用越大,即属性a越重要。因此,可以将定义6中的重要度函数应用于求解伪标签近似质量约简的启发式算法中。详细的算法过程如下所示。
算法1:计算伪标签近似质量约简的启发式算法。
输入:伪标签邻域决策系统NDSPL,半径σ。
输出:伪标签近似质量约简B。
步骤1B←∅;
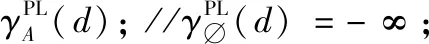

(1) ∀a∈A-B,计算其属性重要度 SigPL(a,B,d);
(2) 选择属性b,满足SigPL(b,B,d)=max{SigPL(a,B,d)∶a∈A-B};
(3)B←B∪{b};
EndWhile
步骤4 输出伪标签近似质量约简B。
由算法1的过程可知,算法1的主要时间消耗在于计算属性的重要度。因此,算法1的时间复杂度为O(|U|2·|A|2),其中 |U| 和 |A| 分别表示样本和属性的个数。显然,若使用算法1求解一组半径下的约简时,则需要在每个半径上遍历所有属性来寻找满足约束条件的属性子集。此时,随着半径个数增多,这一方法将会具有较高的时间消耗。
2 属性约简加速策略
为解决在1.2节中使用算法1在一组半径上进行属性约简时,求解约简的时间消耗会随着半径个数的增多而增长这一问题,本节将基于启发式算法,考虑在前一个半径下的约简结果基础之上,求解当前半径下的约简,通过减少属性遍历的规模,进行属性约简加速策略的设计,以降低在伪标签邻域粗糙集中求解一组半径下约简的时间消耗。进一步,根据半径的变化趋势设计基于正向和逆向的属性约简加速算法。
2.1 基于正向的属性约简加速策略
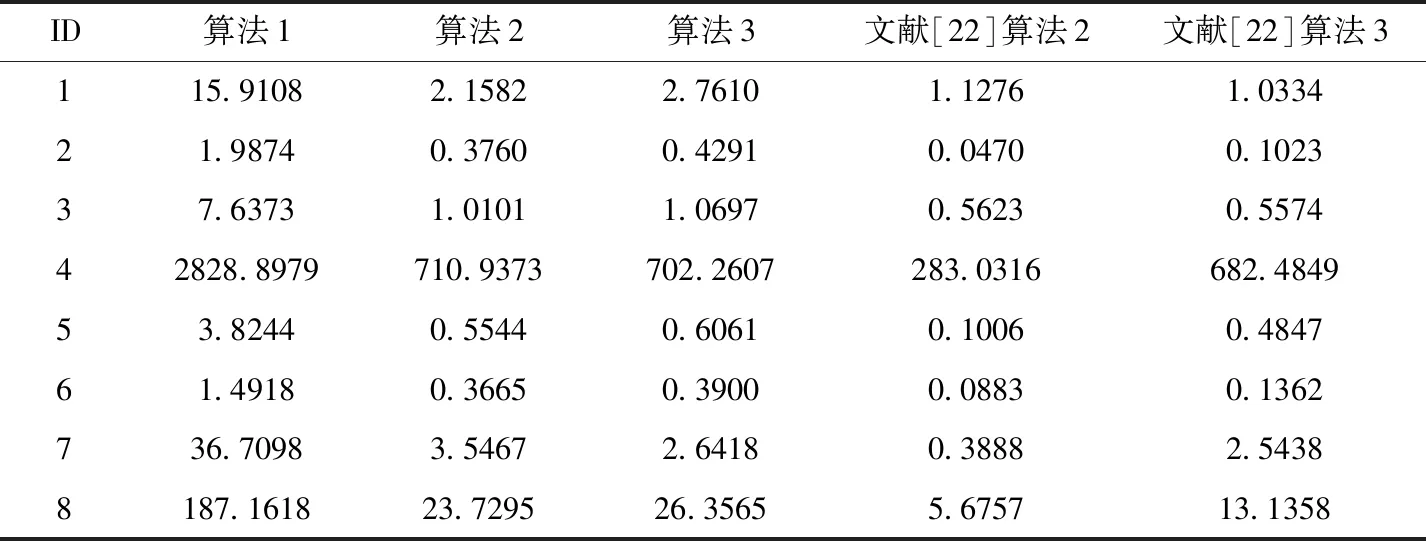
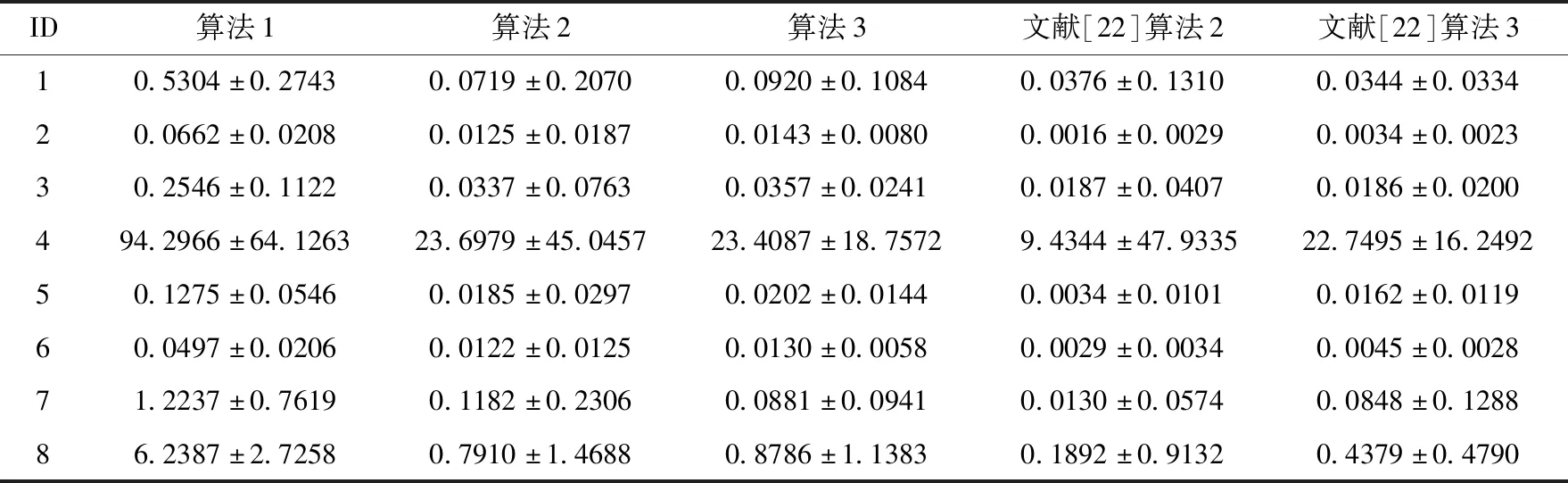
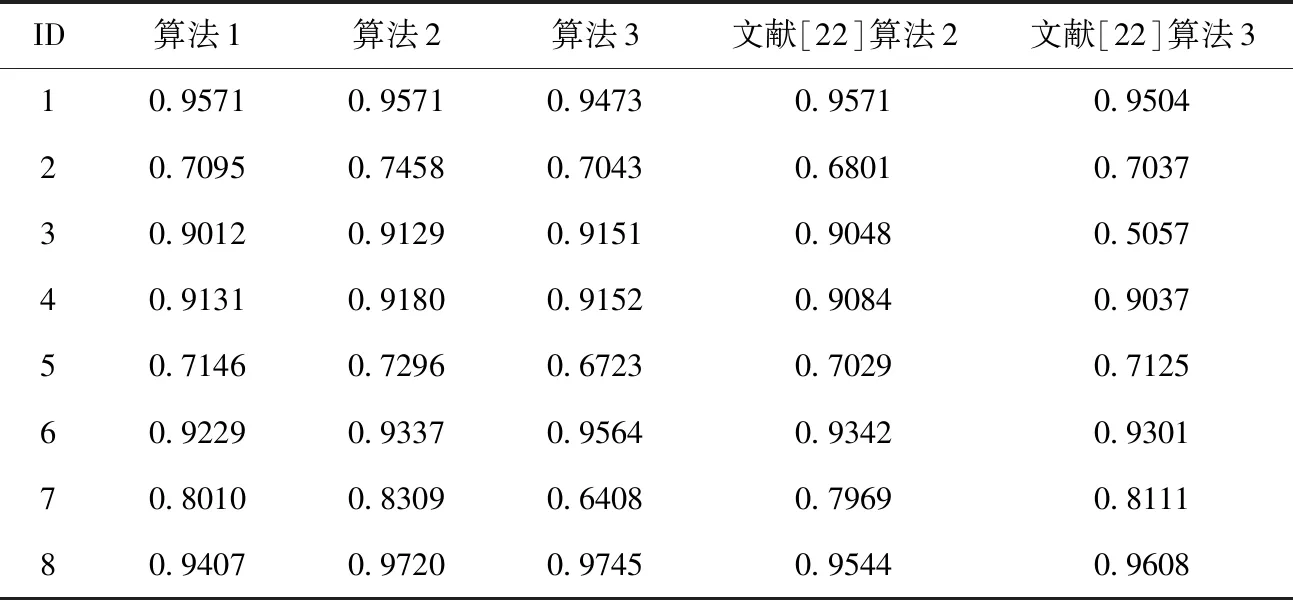
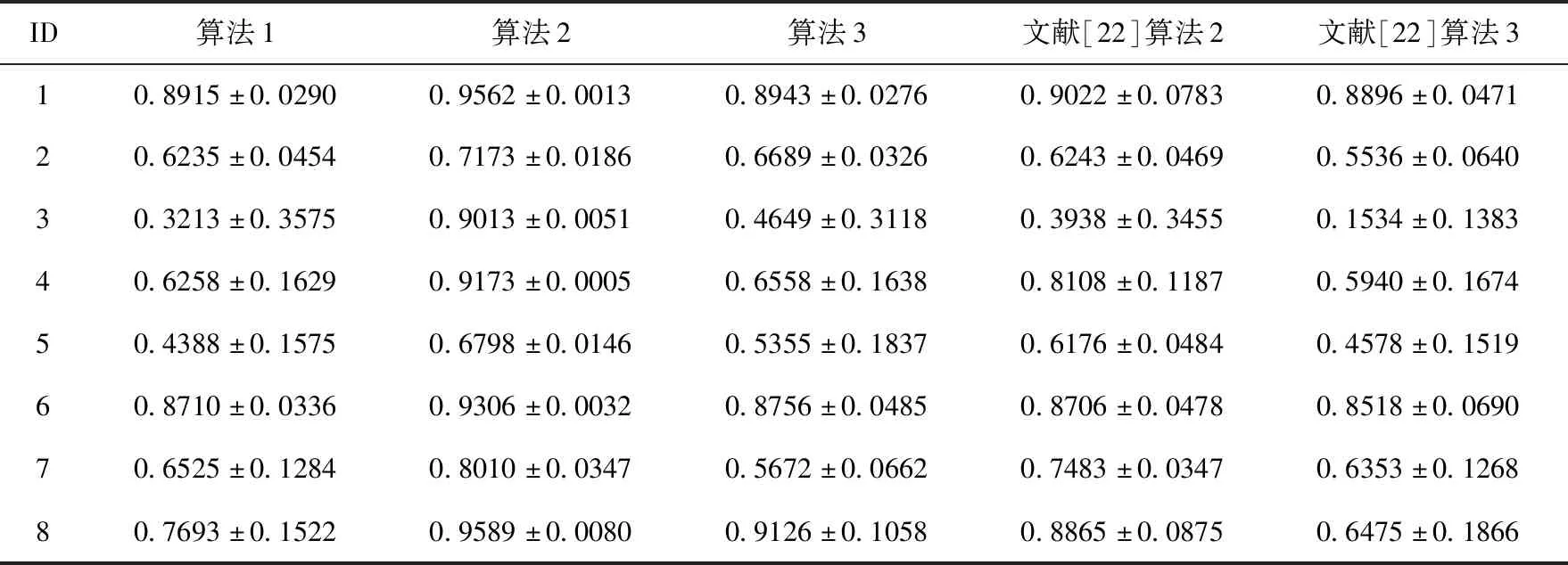
给定一个伪标签邻域决策系统NDSPL和一组半径R={σ1,σ2,…,σn}。假设σ1<σ2<…<σn且在半径σs(1≤s 算法2:基于正向的属性约简加速算法。 输入:伪标签邻域决策系统NDSPL,半径σs下求得的约简Bs,半径σs+1(1≤s 输出:半径σs+1下的伪标签近似质量约简Bs+1。 步骤1Bs+1←Bs; (1) ∀a∈A-Bs+1,计算其属性重要度SigPL(a,Bs+1,d); (2) 选择属性b,满足SigPL(b,Bs+1,d)=max{SigPL(a,Bs+1,d)∶a∈A-Bs+1}; (3)Bs+1←Bs+1∪{b}; EndWhile 步骤4 输出半径σs+1下的伪标签近似质量约简Bs+1。 由算法2的过程可知,算法2与算法1的不同之处在于,当计算某一半径下的约简时,算法2不再是在A中选择具有最大重要度的属性,而是在Bs的基础上,对A-Bs中的属性根据重要度进行选择。由此可知,算法2的时间复杂度为O(|U|2·|A-Bs|2)。 值得注意的是,在基于正向的属性约简加速策略中,当求解最小半径下的约简时,仍需要通过算法1来进行计算。 给定一个伪标签邻域决策系统NDSPL和一组半径R={σ1,σ2,…,σn}。假设σ1<σ2<…<σn且在半径σs(1≤s 算法3:基于逆向的属性约简加速算法。 输入:伪标签邻域决策系统NDSPL,半径σs下求得的约简Bs,半径σs-1(1 输出:半径σs-1下的伪标签近似质量约简Bs-1。 步骤1Bs-1←Bs; (1) ∀a∈A-Bs-1,计算其属性重要度 SigPL(a,Bs-1,d); (2) 选择属性b,满足SigPL(b,Bs-1,d)=max{SigPL(a,Bs-1,d):a∈A-Bs-1}; (3)Bs-1←Bs-1∪{b}; EndWhile 步骤4 输出半径σs-1下的伪标签近似质量约简Bs-1。 由算法3可以看出,基于逆向的属性约简加速策略与基于正向的属性约简加速策略不同之处在于,前者计算一组半径下的约简结果时,是根据半径由大到小的变化趋势进行计算,并在较大半径下的约简基础之上进行下一个半径下的约简求解,而后者与其相反。此外,由算法3的具体过程可知,算法3的时间复杂度为O(|U|2·|A-Bs|2)。 值得注意的是,在基于逆向的属性约简加速策略中,当求解最大半径下的约简时,仍需要通过算法1来进行计算。 为验证所提加速策略的有效性,本节将从UCI数据集中选取8组数据进行实验。数据的描述见表1。在实验中选择了30个半径,它们的值为0.02,0.04,0.06,…,0.60。样本的伪标签是通过k-means聚类方法得到的,其中k的取值与所使用数据集的决策类数相同。此外,本节不仅将第2节所提的加速策略与算法1进行比较,还将与文献[22]中的两种加速算法进行对比。 表1 数据集描述 在本节实验中,为了比较约简结果的分类性能,采用了5折交叉验证。但值得注意的是,由于交叉验证的随机性可能会导致训练集或测试集中某一类样本较少。此时,若根据训练集和约简结果对测试集进行预测,得到的预测结果可能会是不合理的。因此,可以通过对数据进行无偏采样产生训练集和测试集。进一步,5折交叉验证可以通过如下过程进行实现。首先,根据数据中样本的真实标签,将数据分成X1,X2,…,Xp。其次,对任意Xi(1≤i≤p),将其中数据随机平均分成5份,即Xi1,Xi2,…,Xi5。记Tij=Xi-Xij,其中1≤j≤5。最后,在第一轮计算中,将T11∪T21∪…∪Tp1作为训练集进行属性约简,X11∪X21∪…∪Xp1用作测试集,根据约简结果和训练集进行分类;在第二轮计算中,将T12∪T22∪…∪Tp2作为训练集进行属性约简,X12∪X22∪…∪Xp2用作测试集,根据约简结果和训练集进行分类;类似地,在最后一轮计算中,将T15∪T25∪…∪Tp5作为训练集进行属性约简,X15∪X25∪…∪Xp5用作测试集,根据约简结果和训练集进行分类。值得注意的是,本节中的实验结果均为5折交叉验证下所得度量的均值。 在本小节实验中,将使用文中所提及的3种算法和文献[22]中两种加速算法求解一组半径下的约简,并对这5种方法求解一组半径下约简的总时间消耗和平均时间消耗进行对比。详细的实验结果见表2和表3。 表2 约简求解的总时间消耗/s 表3 约简求解的时间消耗/s的均值和标准差 观察表2和表3,可以得到如下结论: (1)分别使用算法2和算法3以及文献[22]中的两种加速算法求解30个半径下的约简时,所消耗的总时间远小于利用算法1求解该组半径下的约简消耗的时间总和。相较于文献[22]中的算法2和算法3,利用文中所提的加速策略求解该组半径下的约简时,所消耗的总时间相对较高。这主要是因为在使用加速策略求解约简的过程中,动态获取样本的伪标签会带来额外时间消耗,这是由伪标签邻域粗糙集模型本身的特性所决定的。 (2)利用文献[22]中的算法2和算法3求解一组半径下的约简,其时间消耗的均值较小,且具有较小的标准差。相较于算法1,利用算法2和算法3求解约简的消耗时间的平均值和标准差相对较小。由此可知,相较于算法1,所提加速策略和文献[22]中加速算法均有助于降低求解一组半径下约简的时间消耗。 在本小节实验中,将利用文中3种不同算法和文献[22]中的两种加速算法求解一组半径下的约简,并比较这5种方法所得约简在测试集上的分类性能。实验中使用的分类器为KNN分类器,K的取值为3。详细的实验结果见表4和表5。值得注意的是,表4比较的是这5种方法在该组半径下得到的分类准确率的最大值,而表5比较的是该组半径下得到的分类准确率的均值和标准差。 表4 分类准确率的最大值比较 表5 分类准确率的均值和标准差比较 观察表4和表5,可以得到如下结论: (1)相较于算法1和文献[22]中的两种加速算法,利用算法2或算法3得到的约简结果对测试集进行分类,能得到略高的分类准确率。而在多数数据集上利用算法1得到的分类准确率略高于或接近于利用文献[22]中的算法2和算法3得到的分类准确率,这主要是因为伪标签策略的引入,有助于提高邻域关系的分辨能力,进而有利于得到具有较好分类能力的约简。 (2)利用算法2求解的约简结果对测试集进行分类,得到的分类准确率的均值高于利用算法1和文献[22]中的两种加速算法得到的分类准确率的均值,而利用算法3在多数数据集上得到的分类准确率的均值略高于利用算法1和文献[22]中的算法3得到的分类准确率的均值。此外,利用算法2得到的分类准确率的标准差小于利用算法1和文献[22]中的两种加速算法得到的分类准确率的标准差,而通过算法3在多数数据集上得到的分类准确率的标准差略低于或接近于利用算法1和文献[22]中的算法3得到的分类准确率的标准差。由此可知,相较于算法1和文献[22]中两种加速算法,所提加速策略不会降低约简的分类能力,并且利用所得的约简对测试集进行分类,能得到相对较稳定的分类结果。 在本节实验中,为比较约简的分类性能,除分类准确率外,将采用G-mean对约简结果提供的分类能力进行对比。因此,在实验中将根据文中3种算法和文献[22]中两种加速算法在训练集上得到的约简结果对测试集中的样本进行分类,并根据分类结果和样本的真实标签计算G-mean。类似于3.1节和3.2节,该组半径下G-mean的最大值、均值以及标准差将用于最终比较。详细的比较结果见表6和表7。 表6 G-mean的最大值比较 表7 G-mean的均值和标准差比较 观察表6和表7,可以得到如下结论: (1)利用算法2或算法3计算约简,然后对测试集进行分类并计算G-mean,相较于表6中的其它3种算法,能得到略高的G-mean值。 (2)通过算法2得到的G-mean均值高于利用算法1和文献[22]中的两种加速算法得到的G-mean均值,且其标准差相对较小。而通过算法3在大多数数据集上得到的 G-mean 均值略高于利用算法1和文献[22]中算法3得到的G-mean均值,并且其标准差相对较小。由此可知,相较于使用启发式算法和文献[22]中两种加速算法,使用文中所提加速策略在计算一组半径下的约简时,所得约简的分类性能并不会降低,且利用约简结果进行分类,得到的分类结果相对较稳定。 在基于伪标签邻域粗糙集的多个半径下进行属性约简时,往往需要在每个半径上遍历所有的属性来寻找满足约束条件的属性子集。显然,这一方法求解约简的时间消耗会随着半径个数的增加而增长。鉴于此,基于启发式方法的搜索过程,通过减少属性遍历的规模,设计了属性约简加速策略。这一策略通过在前一个半径下的约简结果之上求解当前半径下的约简,来减少求解约简的时间消耗,进而提供加速的效果。此外,实验结果表明所提加速策略可以减少求解一组半径下约简所消耗的时间,并且不会降低约简提供的分类能力。在本文的基础上,下一步的工作有: (1)文中仅使用了伪标签近似质量作为属性约简的度量,进一步将采用其它度量如伪标签条件熵、伪标签邻域决策错误率等构造适应度函数,并进行相应的加速算法设计。 (2)文中仅使用了伪标签邻域粗糙集设计属性约简的加速策略,进一步将在其它粗糙集模型如K近邻粗糙集[9]中考虑相应的加速策略。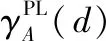
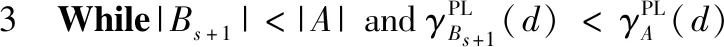
2.2 基于逆向的属性约简加速策略
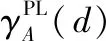
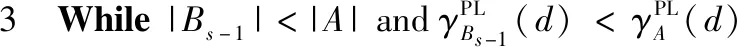
3 实验分析

3.1 算法时间消耗的比较
3.2 分类准确率的比较


3.3 G-mean比较
4 结束语

