基于Runge-Kutta法的输气管道泄漏定位技术研究

吴波 杨旭东 张小芳 司宗庆 牟燕 梁昌晶

1中国石油华北油田公司第三采油厂

2中国石油华北油田公司第一采油厂

3中国石油华北油田公司二连分公司

输气管道的泄漏定位技术是管道完整性管理的重要组成部分，管道防腐层的缺失、阴极保护的失效、土壤介质对管道外壁的腐蚀，以及管输介质对管道内壁产生的腐蚀，均会引起管道不同程度的泄漏[1]。据统计，1995—2005 年，中国石油管道分公司每年大约产生12～15 起重大输气管道泄漏事故，其中2004 年因腐蚀引起的管道泄漏事故就多达20余起[2-3]。目前，已有多种针对管道泄漏的检测与定位技术，但每种检测方法的原理和手段差别较大，同时由于管输天然气组分的多样性，敷设方式的差异性（如埋地、直敷、架空、穿跨越等），以及泄漏方式的多元性（如渗透、穿孔、断裂等），使得各种检测方法在定位精度和检测时间上都存在一定的局限性[4-5]。

韩玲娟等[6]采用分布式光纤传感器对水下输气管道的泄漏进行了有效定位，采用小波神经网络对信号进行了有效提取，用聚类分析判断管道泄漏的严重程度，并采用最小二乘法拟合信号参数进行定位，该方法与传统定位方法相比误报率下降了6.6%；焦敬品等[7]通过对20种不同的泄漏信号进行识别，运用BP 神经网络进行泄漏点的检测和定位，整体识别率≥92.5%；田野[8]设计了一套基于次生波原理的泄漏监测系统，结合了比例-积分-微分（PID）整定调节和自适应算法，对输气管道的泄漏定位误差≤20 m；李凤等[9]将负压波和声波技术进行了耦合，通过前处理软件（ICEM）对管道进行了网格划分，应用计算流体力学（CFD）软件进行了流场变化分析，有效解决了单一信号噪声大、鲁棒性差的缺点。综上所述，管道的定位检测需要在首末点设置大量的传感器，并且采用多种软件进行模型构建和数据模拟，工作量大，一般操作人员较难掌握。

我国大部分输气管道由于管道沿程高差的区别和地理跨度的差异，属于非等温输气管道，随着计算机科学和数值分析理论的不断发展，通过现有传感器测量的温度、压力和流量数据，采用改进的变步长龙格-库塔（Runge-Kutta）法对非等温输气管道进行检测和定位，同时通过实例进行仿真计算，并与传统的负压波检测结果进行对比，以期可以快速、准确地对泄漏点进行定位。

1 模型建立

1.1 输气管道模型

将输气管道中介质的流动视为稳态流动，而稳态流动与时间变量无关，根据流体力学和热力学相关公式建立沿管输方向的稳态流动方程[10-11]。其中连续性方程、动量方程、能量方程和状态方程分别为

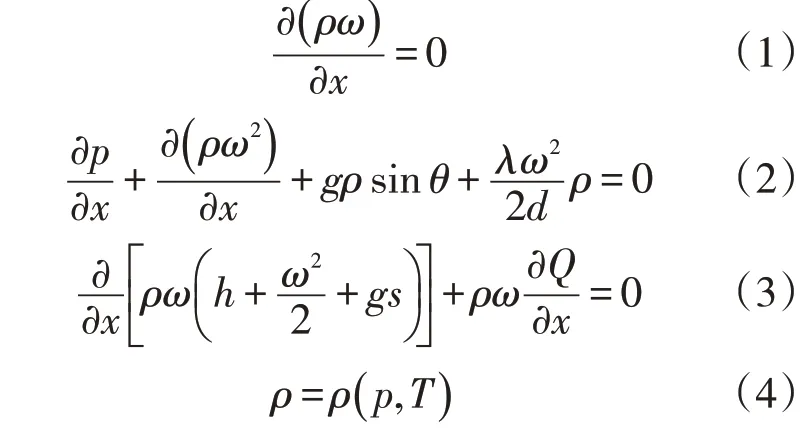
式中：ρ为管输气体密度，kg/m3；ω为气体流速，m/s；x为管道长度，m；p为管输气体压力，Pa；g为重力加速度，取9.8 m/s2；θ为管道倾角，rand；λ为水力摩阻系数；d为管道内径，m；h为管输气体的焓，J/kg；s为管道的位置高度，m；Q为单位质量气体向外界释放的能量，J/kg；T为管输气体温度，K。

在已知气体组分及温度、压力的前提下，可以由实际气体状态方程对气体密度和压缩系数进行求解，比较实用的状态方程有RK、SRK、BWRS 和PR方程，在此采用BWRS方程进行计算[12]。

1.2 Runge-Kutta法

该算法是一种在工程上被广泛应用的高精度单步算法，主要原理是通过对常微分方程组进行离散化处理，求解该方程的初值；随后选择不同的步长，在之间计算多个点的斜率值，将其加权平均作为平均斜率。为了便于计算，通常采用较为经典的四阶Runge-Kutta 进行计算[13]，通过与泰勒级数展开式进行对比后求解未知数，简化后的公式如下

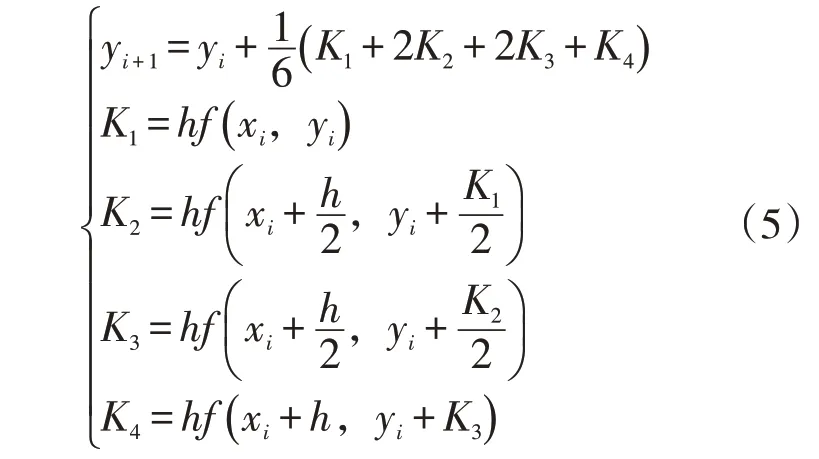
式中：xi、yi分别为自变量和因变量；yi+1为下一个步长的因变量；h为步长系数；K1、K2、K3、K4为待定系数，表示输出变量的一阶倒数。

将管道分成n段，每段管道长度定为Δx（代表每段管道的微元）。Runge-Kutta法的关键是对于Δx的合理选择，单从每一个截断来看，步长越小，截断误差越小，但随着步长的不断减少，计算时间也在不断延长，一定范围内的求解步数也会增加。不同的迭代计算会导致舍入误差的大量累计，在计算效率和精度上有很大缺陷，因此首先设置较大的计算步长，在整个管段内进行泄漏位置的初选，随后逐步缩小泄漏定位的搜索范围，直到满足定位精度的要求，一般取0.5%～1%的初始步长进行运算。

在经典四阶Runge-Kutta 算法的基础上采用精细Runge-Kutta 法计算，该方法融合了精细积分法和Runge-Kutta 法的优点，可以将特解的数值代入Runge-Kutta公式中积分，并利用Runge-Kutta法对数值积分点的未知参数进行预估，得到更精细的算法。根据现场传感器采集到的管道起点温度Ti、压力pi和流量mi，计算从起点到末点管道各截面的温度、压力和流量数值。首先计算第一个微元Δx1的斜率k1，从第一个积分点出发，前进半个步长，得到第二个积分点的预测斜率k2；然后以k2为基础，再次从第一个积分点出发，前进半个步长，重新计算第二个积分点的预测斜率k′2；将两次计算的k2和k′2进行加权平均，作为第二个积分点的近似斜率；以此类推，直到计算出最后一个积分点也就是管道末点的温度、压力和流量数值。其中以第一个微元管道Δx1为例，运用Runge-Kutta法求解公式（1）～（4）来计算管道截面的参数，公式如下

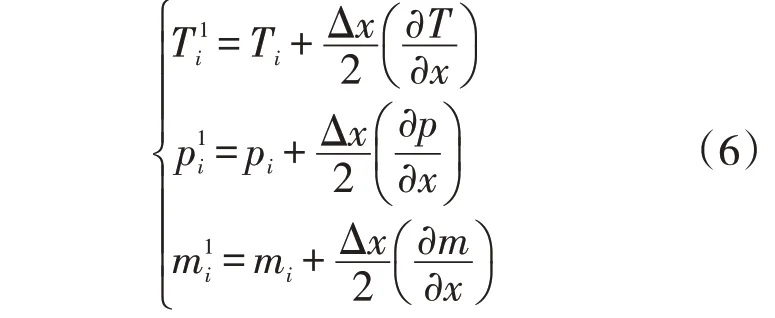
以此类推，得到管道末点的温度Ti+1、压力pi+1和流量mi+1的计算公式如下

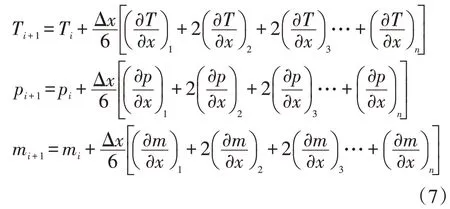
从管道起点开始，运用Matlab 对公式（7）进行反复的迭代计算，即可完成从管道起点到末点不同截面的温度、压力和流量的计算；从末点到起点的参数计算也类似，只是将公式（2）～（3）的摩擦阻力项和热损失项进行调整，具体见式（8）～（9），这种模型非常适合非等温输气管道的模拟和仿真。

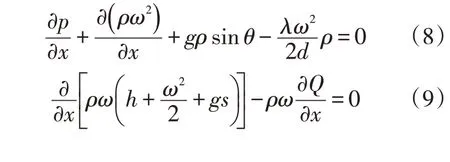
2 泄漏定位算法

通过现场传感器采集到的起点温度Ti、压力pi和流量mi，依据Runge-Kutta法计算末点管道的温度、压力和流量，同样通过采集到的末点温度Tn、压力pn和流量mn，反算起点管道的温度、压力和流量，得到图1。

图1 泄漏定位原理Fig.1 Leak location principle

假设在某一时刻t，由管道末点计算到管道起点的参数为Tnt、pnt、mnt，将判断泄漏事故发生的压力阈值定义为εt，则判断泄漏的边界条件为

当公式（10）成立，表示管内无泄漏点；当存在泄漏点时，管道内各点的相关参数会偏离计算结果，式（10）不再成立。当pnt＜pn时，管道内存在泄漏点。在管道的运行过程中，难免会出现关停压缩机或停输再启动等工况，此时的监测数据会有较大波动，容易产生误报，因此不考虑改变操作引起的扰动在时间内的报警，t1为泄漏点传播到起点的时间，t2为泄漏点传播到末点的时间，t3为扰动的熵变传播到末点的时间，n为划分管道的段数，Δt为报警阈值。

图1 中L1代表未发生泄漏时的压降，L2代表泄漏发生后从起点计算到末点的压降，L3代表泄漏发生后从末点计算到起点的压降。当发生泄漏时，泄漏点处气体的密度和压缩系数会发生变化，压力也会发生瞬变。对于L2，泄漏点之前的仿真结果无限接近L1，泄漏点之后的仿真结果偏离L1，且距离x0越远，偏离程度越严重；对于L3，泄漏点之后的仿真结果接近L1，泄漏点之前的仿真结果偏离L1，L2、L3的交点为x0即为泄漏点。泄漏定位流程图见图2。

3 实例计算

华北油田采油二厂从别古庄到霸一联的输气管道全长2.7 km，管道规格为Φ213 mm×5.5 mm，管道输量200 m3/min，实际运行压力0.4～0.8 MPa，管输介质成分CH4占98%，另外还有少量的C2H6、C3H8等。利用管线全面清管期间，在一些特定位置（充分考虑安全、环保的要求）人工制造几处泄漏点，通过球阀控制泄漏过程。为了避免放气时间与信号采集不同步，先进行阀门放气，一段时间后关闭阀门，设置首站压力0.65 MPa。图3 和图4 分别为泄漏点位于40.5 m时，发生泄漏后管道起点和末点的压力随时间变化的曲线。

图2 泄漏定位流程图Fig.2 Flow chart of leak location

图3 起点压力随时间变化曲线Fig.3 Change curve of start point pressure with time

图4 末点压力随时间变化曲线Fig.4 Change curve of final point pressure change with time

由图3 和图4 可知，在15 s 处管道发生泄漏，15～25 s 的时间段内首末点压力急剧下降，而后趋于平稳，可见整个泄漏过程经历了稳态—快瞬态—慢瞬态—稳态四个过程，流体从恒定流状态向瞬变流状态转变，稳定之后的压力值低于泄漏前的压力值。为了更好地验证改进后的Runge-Kutta 法对泄漏定位预测的准确性，控制阀门开度，以不同的泄漏率（即泄漏孔径与管径的比值）对模型进行验证，同时与传统的负压超声波定位精度进行对比，结果如表1所示。

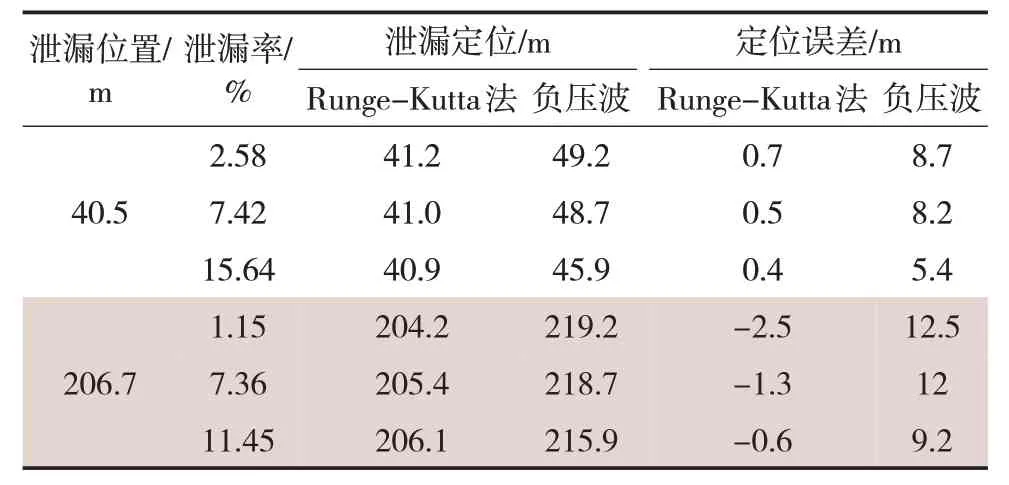
表1 不同泄漏率下泄漏定位结果对比Tab.1 Comparison of leakage location results under different leakage rates

由表1可知，在泄漏位置一定的情况下，随着泄漏孔径和泄漏率的增加，Runge-Kutta 法和负压波定位的定位误差都在逐渐变小，通过结果对比，Runge-Kutta 法的定位误差为0.4～2.5 m，小于传统的负压波定位误差（5～12 m）。

地形地貌及管输介质成分的不同决定了实际工况下的输气管道大多数为非等温管道，为考察首末段温差对定位精度的影响，在泄漏位置和泄漏率一定的前提下，通过提高首站和末站的温度，在泄漏率5%的条件下用Runge-Kutta法和负压波对泄漏进行定位，结果如表2所示。

由表2可知，随着首末点温差的不断增加，两种方法的定位误差也随之增大，但Runge-Kutta 法在定位精度上明显优于负压波定位，因此在温差较大的情况下，Runge-Kutta 法可用于非等温输气管道的泄漏检测和定位。

管道输量的大小对于不同泄漏孔径也有一定影响。控制首站流量为150～300 m3/min，在泄漏率5%条件下，首站压力设置为0.5～0.7 MPa，对326 m处的泄漏点进行定位，结果如表3所示。

表2 首末点温差变化对定位精度的影响Tab.2 Influence of temperature difference between start and final point on positioning accuracy

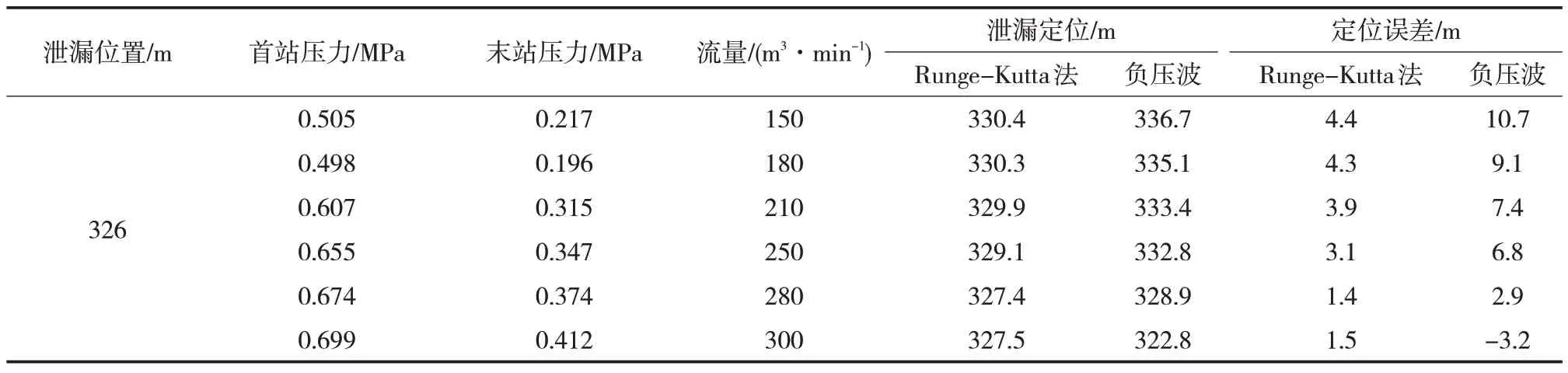
表3 不同管道输量对定位精度的影响Tab.3 Influence of different pipeline volumes on positioning accuracy

由表3可知，随着管道输量的不断增加，定位误差整体减小。这是因为输量越大，管道内的气体流速越大，在泄漏孔处的流出速度越大，压力波动越明显。

综上所述，对比不同情况下的定位误差，对定位精度的影响因素排序由大至小是管道输量、泄漏率、首末点温差。

4 结束语

（1）通过采集到的首末点温度、压力和流量数据，应用改进后的Runge-Kutta 法可以计算管道各点的压力分布，进而对泄漏点进行有效定位，该方法原理简单，对现场操作人员的专业要求不高，易于实现，与传统的负压波相比具有一定的优越性。

（2）泄漏定位技术涉及多学科的融合和交叉，不应只注重现场传感器的数据，随着机器学习、数值分析的发展，今后应加强各学科之间的融合，提高定位精度。

（2）该方法只适用于干气管道，对于含液较多的管道由于气液流速不一致、气液滑脱等现象并不适用，同时对于同一时刻有多处泄漏点的数据扰动考虑不足，今后应深入研究，加强模型的完善以提高定位精度。