高压开关紧固螺钉预紧力拆卸力矩值异常分析与计算

(1.上海思源高压开关有限公司，上海 201108；2.思源电气股份有限公司，上海 201108)

0 引 言

高压开关产品中，法兰与法兰之间、内部零件之间的连接一般都是通过螺钉进行紧固，但在高压开关动热稳定试验后或放置一段时间后，对高压开关产品进行拆解时发现，螺钉的拆卸力矩值小于标准紧固力矩值。

下面以三相共箱高压开关母线动热稳定试验样机为例，在动热稳定试验后发现产品内部的部分螺钉发生松动，分析螺钉松动的原因，并根据相关资料归纳螺钉在交变载荷作用下的预紧力计算模型。

1 螺钉松动原因分析

1.1 螺钉拆卸力矩值[1]

首先分析螺钉传动的运动模型。螺旋传动需有力矩或作用力才能实现相对运动，如图1所示，螺纹传动可做简化变化，如图1(b)所示，作用在中径的水平推动力推动斜面上的物体沿螺纹运动。将螺纹沿中径展开，可得图1(b)中的角度为ψ的斜面。图1(b)中ψ为螺纹升角；Fa为轴向载荷(其最小值为斜面上物体的重力)；F为作用于中径处的水平推力；Fn为法向反力；f·Fn为摩擦力；f为摩擦系数；ρ为摩擦角；f=tanρ。

当图1(b)上的物体向上移动时，Fa为阻力，F为水平的推力。因摩擦力沿斜面向下，故总的反力为FR与Fa的作用力之和，夹角为ψ+ρ。按力的平衡条件进行计算，FR、F和Fa三力的关系如图1(b)所示，由图1可得：

F=Fatan(ψ+ρ)

(1)

作用在螺旋副上的推动力的力矩为

(2)

式中，d2为螺纹中径。

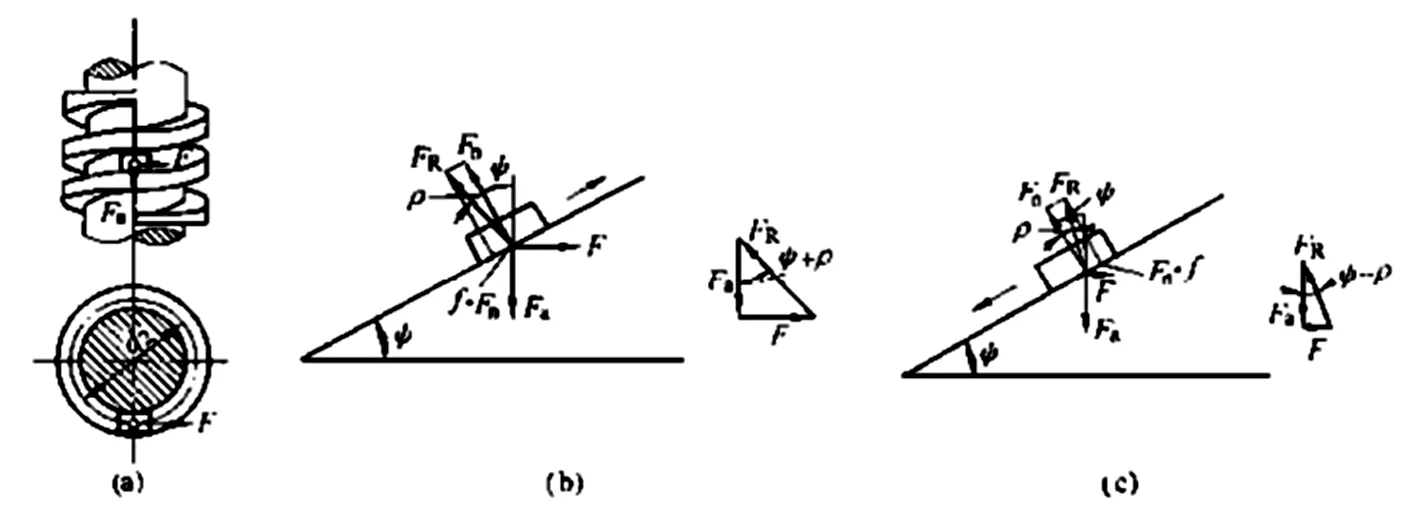
图1 矩形螺纹的受力分析(适用于三角螺纹)

当图1(b)斜面上的物体沿斜面以匀速向下滑动时，轴向的力Fa由之前的阻力转变为向下的动力，而水平推力F由之前的动力转为阻力，水平推力F也是维持图1(b)斜面上的物体以匀速向下滑动所需要的平衡力(如图1(c))。由图1(c)中的关系可得式(3)和式(4)：

F=Fatan(ψ-ρ)

(3)

作用在螺旋副上的推动力的力矩：

(4)

式(3)求出的F值可为阻力，也可为推力。当斜面的水平夹角ψ大于摩擦角ρ时，图1(b)斜面上的物体受Fa的力，而Fa的方面朝下，故使斜面上的物体向下加速运动。这时由式(3)求出的水平力F为阻力，方向如图1(c)所示。它阻止图1(b)斜面上的物体加速以便保持匀速下滑。当斜面倾角ψ小于摩擦角ρ时，图1(b)斜面上的物体不能在重力作用下自行下滑，即处于自锁状态。这时由式(3)求出的力F为推力，其方向与运动方向的夹角小于90°，在这种情况下F就成为推力了。说明在自锁条件下，必须施加反向推力F才能使图1(b)斜面上的物体匀速向下滑动。

以上讨论适用于矩形螺纹连接形式，而常用螺纹为三角形螺纹。三角螺纹的受力分析与矩形螺纹相同，但其摩擦系数f′比矩形螺纹的摩擦系数f大一些，换算公式为

(5)

式中，ρ′为当量摩擦角。

当图1(b)斜面上的物体沿非矩形螺纹等速上升时，可得水平推力为

F=Fatan(ψ+ρ′)

(6)

相应的推力矩为

(7)

当图1(b)斜面上的物体沿非矩形螺纹等速下滑时，可得：

F=Fatan(ψ-ρ′)

(8)

相应的推力矩为

(9)

与矩形螺纹分析相同，若螺纹升角ψ小于当量摩擦角ρ′，这种情况下螺纹自锁，如无外部力矩推动，则轴向推力Fa即使施加很大力值，都无法推动螺旋副进行相对运动。考虑到极限特殊情况，三角形螺纹的自锁条件可表示为

ψ≤ρ′

(10)

为了防止螺母在沿中心线方向的力值作用下自行松开，三角形螺纹联动需满足自锁条件。

以上分析适用于三角形螺纹连接，归纳起来就是：当轴向载荷为阻力时，则会阻止三角形螺纹连接传动相对运动，相当于图1(b)斜面上的物体沿斜面匀速上升，应使用式(2)或式(7)；当轴向载荷为推力时，当与三角形螺连接传动相对运动方向一致时，相当于图1(b)斜面上的物体沿斜面匀速下滑，应使用式(4)或式(9)。

三角形螺母与螺钉紧固时，螺母上的紧固力矩T等于三角形螺纹转动的阻尼力矩T1加上螺母在接触面上的摩擦阻尼力矩T2，即：

(11)

式中：Fa为沿螺钉中心线的力值，对于不承受轴向载荷的三角形螺纹，Fa即为预紧力；d2为螺纹中径；fc为螺母与接触面之间的摩擦系数；rf为支撑面摩擦半径。

同理，拆卸螺钉所需的力矩为

(12)

针对三角螺纹，f′值一般取0.15，得出ρ′为8.5°，而单线普通螺纹的升角约在1.5°～3.5°之间，所以螺纹的拧紧力矩值必然大于其拆卸力矩值。

1.2 温度对螺钉联接预紧力的影响[2]

高压开关常用的螺钉联接主要有2种方式，一种为螺栓-螺母联接，如图2(a)所示；另一种为螺钉-盲孔联接，如图2(b)所示。被联接件为铝合金板，联接螺钉为钢，下面分析温度的变化对这2种方式紧固联接预紧力的影响。

图2 常用的2种紧固联接方式

1.2.1 螺栓-螺母联接方式

此种型式的螺栓与被联接件的材料线膨胀系数不同时，就会在螺栓和法兰密封件之间由于热胀冷缩产生不同的变形。这种变形在热胀时不会引起紧固不牢的情况，但在冷缩时螺栓的线膨胀系数小，变形就小，而法兰密封面线膨胀系数大，变形就大，从而使螺栓、螺母的紧固松弛。

1)温度变化所引起的热胀冷缩变形如图2(a)所示，为法兰在螺栓与螺母紧固情况下的示意图。螺栓预紧时的环境温度为t0，实际运行时的环境温度为t。因螺栓与被紧固的法兰线膨胀系数存在差异，螺栓在轴线方向的变形量与法兰的变形量存在差异。

假设温度引起的热变形在弹性范围内，则螺栓相对于被联接件的热弹伸长变形为

Δλt=λt1-λt2=(α1-α2)(t-t0)l

(13)

式中：λt1为螺检的变形量；λt2为被联接件的变形量；α1为螺检的热膨胀系数；α2为被联接件的热膨胀系数；t0为初始温度；t为变化后的温度；l为被联接件或螺栓紧固段的有效长度。

被联接件为铝合金，螺栓为钢，由于铝合金的热膨胀系数(2.2×10-5～2.4×10-5/℃)大于钢的热膨胀系数(1.06×10-5～1.22×10-5/℃)，所以当温度变化时，被联接件的伸缩量要大于螺栓的伸缩量。

2)温度降低对螺栓预紧力的影响

温度降低时，法兰和螺栓发生冷缩，由于铝合金的热膨胀系数大于钢的热膨胀系数，螺栓预紧力将发生松弛。松驰量公式为

(14)

图3 温度降低对初始预紧力及变形的影响

图4 温度降低热弹变形的简化力-变形线图

由图4可知：

(15)

即：

(16)

热弹变形差Δλt与螺栓和被联接件的虎克变形之间的关系：

Δλt+λ1′+λ2′=λ1+λ2

(17)

或：

Δλt=(λ1-λ1′)+(λ2-λ2′)

(18)

由式(18)可知：热胀引起的法兰伸长量-热胀量引起螺栓伸长量=预紧力松弛引起的螺栓缩短量+预紧力松弛引起法兰缩短量。

3)温度升高对螺栓预紧力的影响

当温度升高时，被联接件和螺栓同时发生膨胀，由于被联接件铝合金的热膨胀系数大于螺栓的热膨胀系数，所以被联接件的变形量大于螺栓的变形量，此时，Δλt<0，预紧力将由原来的Qp增加为Qp′，同上节所述可以获得如图5所示的力-变形线图。

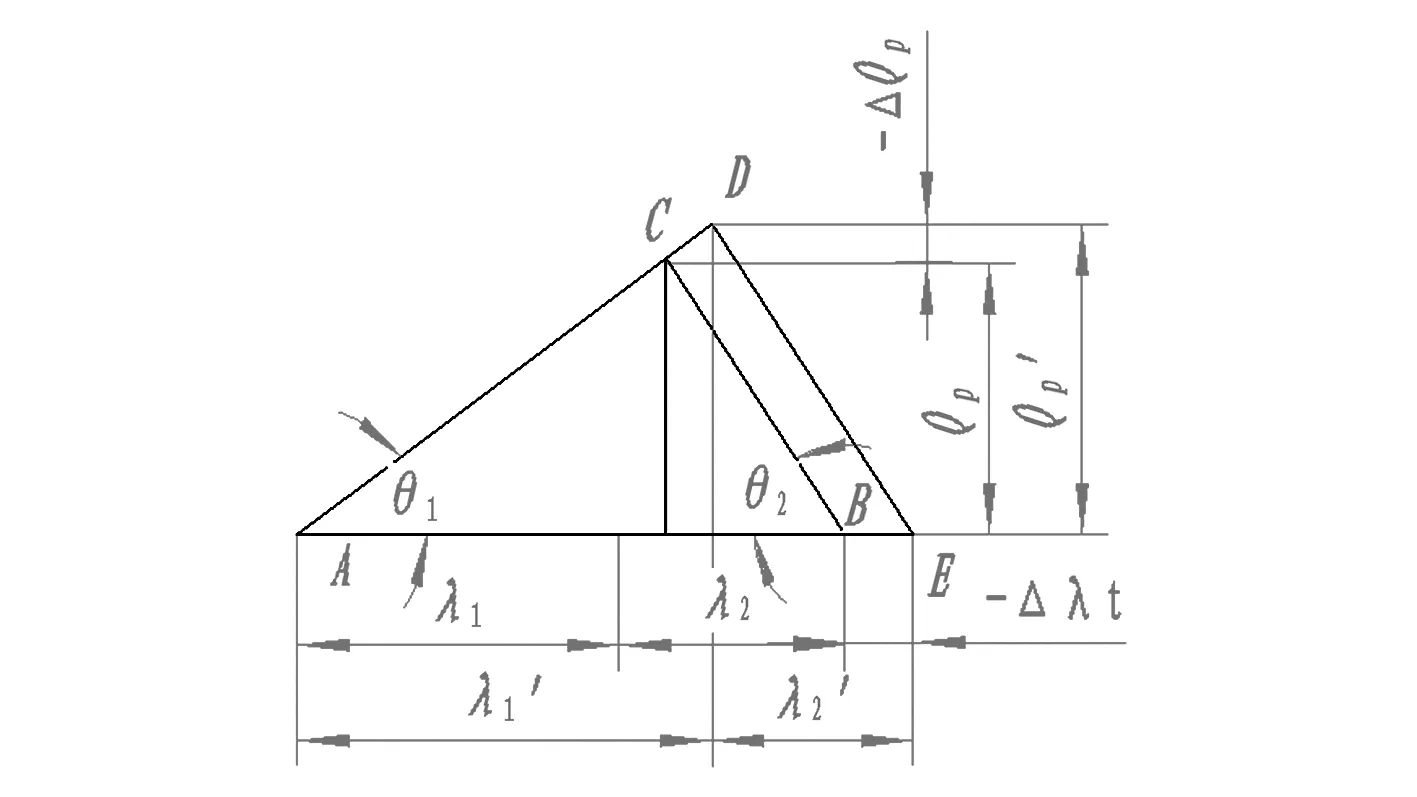
图5 温度升高热弹变形的简化力-变形线图

这样，只要求出Δλt，用图解法就可以直接求出预紧力增量-ΔQp以及温度升高后实际预紧力Qp′。 ΔQp的解析式同式(15)、式 (16)，其值为负。

综上所述，当采用螺栓-螺母联接时(被联接件为铝合金，螺栓为钢)，温度升高会使螺栓预紧力增大，温度降低会使螺栓预紧力变小。根据式(11)、式(12)预紧力Fa的值和拆卸力矩值成正比，所以温度升高会使螺栓拆卸力矩值增大，温度降低会使螺栓拆卸力矩值减小。

1.2.2 螺钉-盲孔联接方式

螺钉-盲孔联接比螺栓-螺母联接复杂得多(暂未找到合适的计算模型)。同样假设被联接件为铝合金，由于螺钉与盲孔的材料不同，温度变化时，2种材料的热膨胀系数不同导致了螺纹膨胀量不同，此时螺纹副相对转动的阻力矩发生变化，螺钉联接的预紧力矩值也发生变化。

三角形螺母与螺钉紧固时，螺母上的紧固力矩T等于三角形螺纹转动的阻尼力矩T1加上螺母在接触面上的摩擦阻尼力矩T2。

当温度降低时，铝合金盲孔收缩，增大螺纹副相对转动的阻力矩，同时铝合金被联接件的体积收缩又会引起预紧力值的降低；温度升高时，铝合金盲孔膨胀，螺纹副相对转动阻力矩降低，但同时铝合金被联接件的体积膨胀将引起预紧力值的增高。这2种因素相互制约、相互影响，目前还无法找到有效的计算模型。

分别以5组螺钉M10与M12为样本进行测试，结果见表1。

根据实际测量数据表明，温度的降低将使螺钉的拆卸力矩值稍有增大，而温度升高对螺钉的拆卸力矩值影响不大。

表1 不同温度下螺钉拆卸力矩实测

1.3 振动载荷作用下螺栓联接预紧力的确定[3]

电场力是母线产生振动的主要原因，在交流电压的作用下，电场力也成周期变化，从而导致导体呈现周期性的振动，而实际装配时母线内部导电杆与绝缘衬垫的间隙有可能放大电场力作用下的振动影响。螺栓联接在振动的工况下，会受到一个交变载荷的作用，这就是螺钉联接产生松动的主要原因。下面将分析振动工况下螺栓联接预紧力的确定。

螺纹联接的稳定性以及自锁功能是建立在静态之上的。当存在振动时，便属于动态自锁问题，螺纹联接的稳定性与自锁功能就会发生转化。当螺栓预紧后，在实际工程状态下，受到动态载荷F时，需要按动态自锁的思路来进行分析，同时还需考虑连接的紧密性，残余预紧力Qp′应根据式(19)[4-5]来确定：

(19)

式中：m为所有联接零件的质量；G为联接所有零件的重量；k为所有联接零件的的总刚度；c为所有联接零件的总阻尼系数。

(20)

Amax为整个工作过程中振动的最大强度，其值为

(21)

式中，Smax和ω分别为振动的最大振幅和频率。

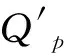
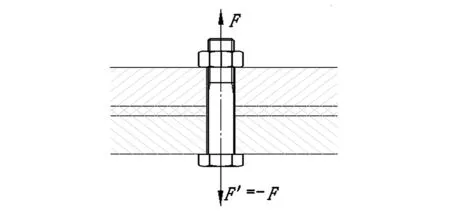
图6 紧固联接受载

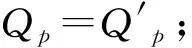
2)当F>0,并当(F，F′)作用于螺栓两端时，需先做出紧螺栓联接受力变形见图7。

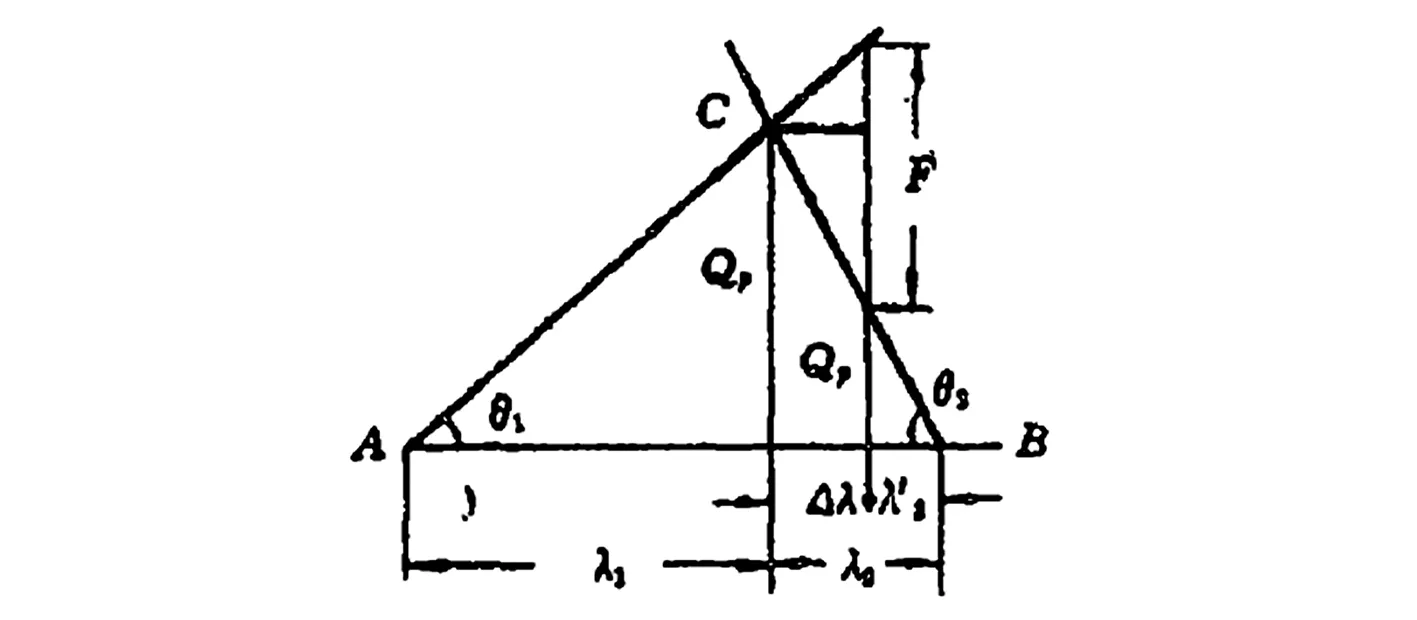
图7 紧螺栓联接受力变形

图7中：λ1为在预紧力Qp作用下螺栓的伸长量；λ2为紧固法兰的压缩量。

于是可得出式(22)关系：

(22)

式中：

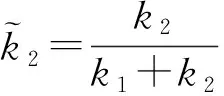
(23)

k1=tanθ1；k2=tanθ2

(24)

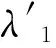
(25)

式中，λ*为两侧连接法兰的变形总和。式(25)相当于从λ2中取出λ*再加到λ1中，而在图8上即是将原图顶点C沿变形坐标轴并向着螺栓变形增大方向平移一个距离λ*，便得出新图。这样，式(22)～式(24)就对应为

(26)

式中：

(27)

而：

(28)

4)当工作载荷为交变载荷时，式(22)和式(26)中的F需理解为拉力的最大值。

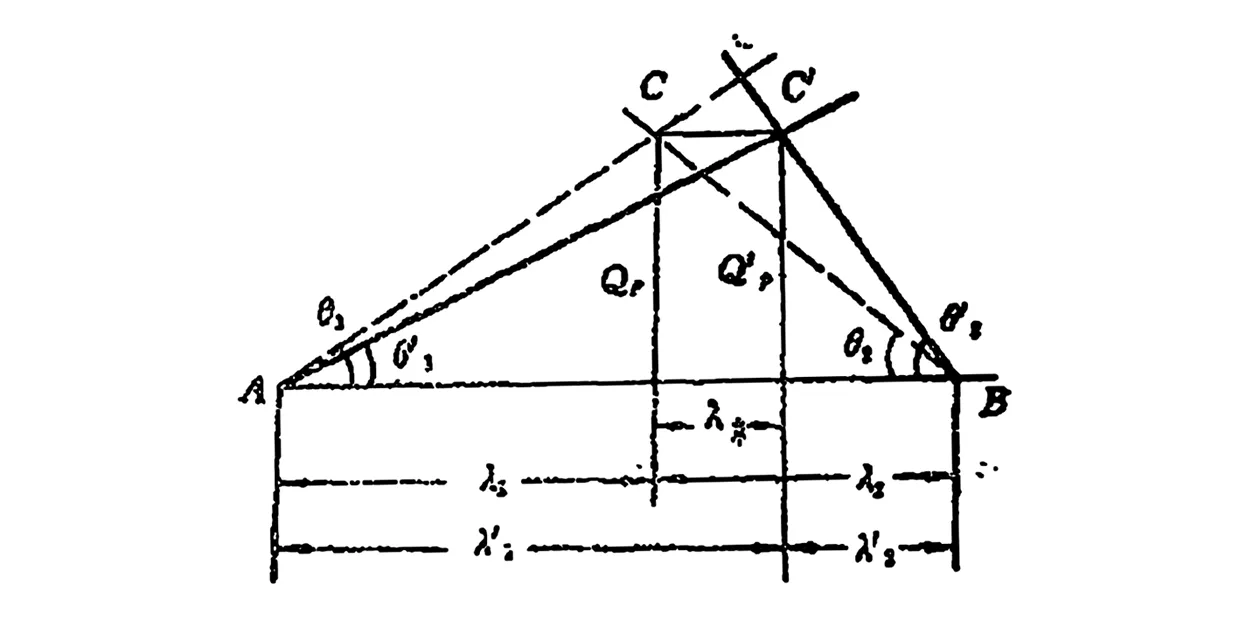
图8 紧螺栓联接受力变形新图

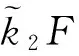
2 相关数值计算

将螺钉的基本尺寸数据带入相关公式，计算螺栓预紧力的相应变化值。

2.1 螺钉拆卸力矩值

要计算螺钉的拧紧及拆卸力矩，首先需要知道螺钉的基本尺寸，以粗牙普通螺纹为例，其基本尺寸如表2所示。

表2 粗牙普通螺纹的基本尺寸 单位：mm

利用式(29)及式(30)可以分别计算出螺钉的拧紧力矩值和拆卸力矩值：

(29)

(30)

将螺钉标准力矩值带入式(11)中可以计算出螺钉预紧力Fa，再将螺钉预紧力值Fa带入式(12)可以计算出不同规格螺钉的拆卸力矩值，计算结果如表3所示。

表3 不同规格螺钉的预紧力值及拆卸力矩

实测M6磷化螺钉的拆卸的力矩值(6次拆卸力矩分别为5.0 N·m、5.2 N·m、5.0 N·m、5.2 N·m、5.4 N·m、4.8 N·m)，与表2对比，说明式(11)和式(12)用来计算螺钉的预紧力矩值和拆卸力矩值，其结果是可信的。

2.2 温度变化及振动工况对螺钉预紧力的影响

利用式(13)、式(16)可以计算温度变化时螺钉预紧力值的变化情况。式(13)、式(16)除了需要材料的本征参数(热膨胀系数等)外还需要用到零件的刚度值k(类似于弹簧的k值)，而该参数与零件的形状和材料密切相关，这里不再对其进行详细的计算。但由计算模型可知，当被联接件为铝合金件时，温度升高的情况下应将预紧力值增加，温度降低的情况下应将预紧力值减小。

同样振动工况下的预紧力计算式(22)、式(26)也需用到被联接件的总刚度系数及总阻尼系数，这里也不再进行详细的计算。其计算模型表明，当振动载荷等效于拉应力时(F>0)，螺钉预紧力矩应相应增加，或采用有效的防松措施，如涂覆高强度螺纹锁固剂、使用双螺母紧固等。

2.3 螺钉最小预紧力值的确定

对于M10—M68的粗牙螺纹，若取f′=tanρ′=0.15及fc=0.15，则式(11)拧紧力矩可以简化为

T≈0.2Fa·d

(31)

Fa值是由螺纹连接的要求来决定的，不同场合下的预紧力要求不同，具体如下：

1)非振动工况下最小预紧力值

当不存在温度变化时，螺钉的螺纹需满足自锁条件，如式(10)所示ψ≤ρ′，稍施加预紧力就能保证螺钉使用过程中不发生松动，即：

Fa(min)>0

(32)

当存在温度变化时，螺钉的最小预紧力应大于温度变化所造成的预紧力减小值，即：

(33)

2)振动工况下的最小预紧力值

当不存在温度变化时，螺钉的预紧力应大于残余预紧力及工作载荷的共同作用力，即：

(34)

当存在温度变化时，螺钉的最小预紧力应大于温度变化所造成的预紧力减小值，即：

(35)

在设计时，为了保证螺钉强度与紧固的可靠性，一般选择在预紧力的作用下螺钉的应力允许值为材料屈服极限值的70%以上，同时考虑在承受工作载荷时螺钉的应力不超过材料的屈服强度。

3 结 语

1)所计算的螺钉拧紧力矩和拆卸力矩与试验结果吻合，实际装配时，拆卸力矩值较紧固力矩值有所降低。

2)对于螺栓-螺母联接方式，当被联接件的热膨胀系数大于螺钉的热膨胀系数时，温度降低将使螺钉预紧力减小，温度升高将使螺钉预紧力值增加；当被联接件的热膨胀系数小于螺钉的热膨胀系数时温度降低将使螺钉预紧力增加，温度升高将使螺钉预紧力值减小。

对于螺钉-盲孔联接方式，没有有效的解析公式，试验结果表明，当被联接件为铝合金件时，温度降低使预紧力值增加，温度升高对预紧力值影响不大。

在设计螺栓-螺母或螺钉-盲孔联接方式时，需考虑温度对预紧力的影响，适当增加或减小预紧力以适配温度。

3)螺纹联接的稳定性以及自锁功能是建立在静态之上的，而高压断路器、隔离开关与母线等模块都受电场力的作用，并存在短路工况，模块就会受到振动工况的影响，螺钉或螺栓如果不采取措施，则会出现松动的情况。因此螺钉或螺母应采取有效的防松措施，如涂覆高强度螺纹锁固剂和使用双螺母紧固。