凸显思维过程 提升核心素养 *
张宗义
(河南省邓州市基础教育教学研究室,河南 邓州 474150)
1 引言
《普通高中物理课程标准(2017年版)》提出:“应把物理课程中所形成的物理观念和科学思维用于分析、解决生活中的问题,在解决问题中进一步提高探究能力、增强实践意识、养成科学态度,促进物理学科核心素养的形成。”教学设计的明晰度、教学实施中逻辑思维的清晰度直接影响课堂教学效率的高低,中学物理教学应体现科学思维培养的导向作用,在引导学生进行科学推理、论证时,把归纳与演绎思维相结合,凸显学生的主体地位,关注学生的思维过程,以下笔者结合具体的案例予以阐述。
2 例题及其解题思维过程
2.1 例题与答案
例题:如图1所示,L1、L2为相互平行的足够长光滑导轨,位于光滑水平面内,一个略长于导轨间距,质量为M的光滑绝缘细管与导轨垂直放置,细管两端的底部有两个光滑卡槽,可使细管在两导轨上左右平动。细管内有一质量为m、带电量为+q的小球,小球与L1导轨的距离为d;开始时小球相对细管速度为零,细管在外力作用下从P1位置以速度v0向右做匀速直线运动。垂直平面向里和向外的匀强磁场Ⅰ、Ⅱ分别分布在L1轨道两侧,如图1所示,磁感应强度大小均为B,小球视为质点,忽略小球电荷量的变化。

图1
(1) 当细管运动到L1轨道上P2处时,小球飞出细管,求此时小球的速度大小;
(2) 小球经磁场Ⅱ第一次回到L1轨道上的位置为O,求O和P2间的距离;
(3) 小球回到L1轨道上O处时,细管在外力控制下也刚好以速度v0经过O点处,小球恰好进入细管,此时撤去作用于细管的外力。以O点为坐标原点,沿L1轨道和垂直于L1轨道建立直角坐标系。求小球和细管速度相同时,小球的位置(此时小球未从管中飞出)。

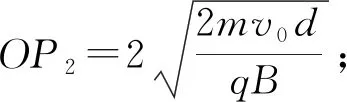

2.2 思维过程分析
2.2.1 搜寻信息,分解过程
引导学生审题,探寻“细管内有一小球”“细管向右做匀速直线运动”“小球经磁场Ⅱ第一次回到轨道上”“小球恰好进入细管,此时撤去作用于细管的外力”等关键信息,理解了这些关键信息就可分析出本题涉及的三个物理过程:
(1) 球在细管内运动,并随细管做匀速运动;
(2) 小球在磁场中运动;
(3) 小球进入细管到与细管速度相同。
2.2.2 分析过程,建构模型
对小球进行受力分析,结合初始运动状态来分析其运动性质,从而建构出三个“运动模型”:
(1) 小球在细管内的匀加速运动与随细管匀速运动的合运动;
(2) 小球在匀强磁场中做匀速圆周(圆弧)运动;
(3) 小球从进入细管到与细管速度相同的过程中做变速运动。
2.2.3 基于模型,应用规律
每个运动模型都有与之相对应的运动规律,分别是:
(1) 小球在细管内做匀加速运动,满足匀变速直线运动的规律;
(2) 小球在磁场中做匀速圆周运动,洛伦兹力提供向心力,满足牛顿第二定律;
(3) 小球从进入细管到做与细管速度相同的过程中,洛伦兹力不做功,小球、细管组成的系统遵从能量守恒定律和动量定理。
2.2.4 基于物理规律,进行科学思维
(3)小球再次进入细管到与细管速度相同的变速运动过程中,如何求出它们末态的共同速度vxt?
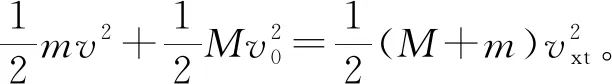
对于变速运动在初、末状态速度确定的情况下,除了从能量视角来列出方程外,还有没有别的方法?讨论后学生提出:可从运动与相互作用的视角来思考,由于在两个方向上此系统所受的合外力不为零,因此不能应用动量守恒定律,只能用动量定理来解决。教师鼓励学生独立尝试解题过程,学生写出了动量定理的表达式。在一极短时间Δt内,在x方向上有:qvyBΔt=(M+m)Δvx,在y方向上有:-qvxBΔt=mΔvy,因Δt极短,可认为物体速度不变,因此有:vyΔt=Δy,vxΔt=Δx。对于所研究的整个过程,小球的初始位置坐标为(0,0),在x、y方向上的速度分量分别为v0、vy0。末位置坐标为(x,y),在x、y方向上的速度分量分别为vxt、0。对此过程在x、y方向上分别求和得:qB(y-0)=(M+m)(vxt-v0),-qB(x-0)=m(0-vy0),由此可得x、y的表达式。
2.2.5 基于质疑,反思内化
解题初步完成后,引导学生检视自己的思维过程,及时进行反思,提升能力,让学生完成学案上的表1,表中后三列内容为学生自主填写,最后师生共同完成求解过程。
2.3 题目拓展
心理学家布鲁纳说过:“向学生提出挑战性的问题,可以引导学生发展智慧。”该题可从以下几方面进行拓展:
(1) 画出小球从开始运动到飞出细管瞬间的运动轨迹;
(2) 当细管由P1匀速运动到L1轨道上P2处的过程中,作用在细管上平行于导轨L1、L2的水平外力如何随时间变化?表达式是什么?
(3) 设细管在P1处时t=0,画出其所受外力随时间变化的图线;
(4) 求P1、P2间的距离;
(5) 若小球由P2点又回到L1轨道上O处,求它在磁场Ⅱ中的运动时间;

表1
(6) 求在小球由P2点回到L1轨道上O处的这段时间内细管运动的平均速度。
针对第(3)问还可以引导学生总结运用牛顿第二定律的途径,培养学生从多个视角思考问题,能够灵活运用不同方法解决问题。通过上述一系列问题的情境创设与解决,提高学生的思维能力。
3 结语
物理学科核心素养中科学思维是灵魂,科学思维方法包括比较与分类、分析与综合、抽象与概括、归纳与演绎、批判性思维等,是形成概念、建构模型的重要方法。高中物理解题过程主要为:(1) 选定研究对象(分类);(2) 分析受力和过程(分析);(3) 构建运动模型(抽象);(4) 立出数学关系式(演绎);(5) 求解检验(质疑)。
与之对应,笔者把其中的思维过程总结为5步:(1) 提取信息,分解过程;(2) 分析过程,建构模型;(3) 基于模型,应用规律;(4) 基于规律,科学思维;(5) 基于质疑,反思内化。
习题教学要为科学思维能力的培养服务,通过具体的问题解决,逐步培养学生应用科学思维方法解决问题的意识和能力。

