面向智能工厂应用的启发式板材排样优化算法
高 勃,张红艳,赵宏军,孙嘉玉,李云志,朱明皓
(1.北京交通大学 a.计算机与信息技术学院,b.经济管理学院, 北京 100044;2.北京机械工业自动化研究所有限公司,北京 100120;3.国家工业信息安全发展研究中心 系统所,北京 100043)
在智能制造过程中,企业为提高经济效益,需要最大化地节约成本,给出企业合理的订购原材料的方案,减少材料浪费,提高企业效益.二维排料广泛应用于汽车制造、造船、钢铁切割、服装设计剪裁,家具下料[1]等工业设计与生产中,属于典型的NP完全问题.对二维排样进行优化是必要的,以此来提高
板材的利用率.在工业生产实践中,有许多因素会影响原材料的利用率,比如操作人员的技术能力,设备的切割误差,排样方案等,其中排样方案的好坏对原材料的利用率起着决定性的作用.
目前国内外学者对矩形件优化排样问题做了广泛的研究,最初的排样算法往往根据矩形件信息进行直接排样,例如文献[2]提出基于动态分割和合一的排样算法.文献[3]提出贪婪算法进行矩形件的排样,每次排样时优先选择面积最大的矩形件,以此来实现板材利用率最高的目标.虽然算法简单,但板材的利用率低.而后采用较多的方法是文献[4-7]所提到的模拟退火算法,遗传算法,蚁群算法等智能算法.虽然智能算法的应用使得板材利用率有所提高,但智能算法计算开销较大,随着企业的生产规模变得越来越大,排料系统的可行性往往会因为计算时间的剧增而不再具有实用性.近几年学者根据零件特征对板材进行启发式填充处理,比如文献[8]改进了在矩形件排样中的填充算法.文献[9]提出矩形件简单块占角排样方式的动态规划.文献[10]采用基于粗糙集的矩形件优化填充排样方法.文献[11]提出了启发式动态分解算法,根据矩形件对板材进行正交动态分解,计算放置耦合度选择最佳子板,通过干涉关系对待排子板状态更新.上述研究虽已取得一定的成果,但应用不具有普遍性,仍存在一定的问题.
基于以上分析,本文作者深入研究了在二维板材下矩形的问题,以最大化板材利用为目标,建立优化排样模型,在此基础上提出了一种新的排样算法——启发式板材排样优化算法,以最大化板材利用率为目标,设计评价函数,通过比较评价函数值进行剪枝优化,加快排样过程中零件的定位及定序,进而缩短时间,给出企业合理订购原材料的方案,并通过案例分析验证了该算法的有效性.
1 二维规则板材排样问题与数学描述
1.1 问题描述
面对节约性和可持续发展的要求,在智能工业生产过程中,以减少原材料浪费为目标,给出企业合理的原材料调度与储备方案,需要在平面区域内给出零件排列的最优布局,最大化利用板材,减少材料的浪费.实际生产中,排料的种类有很多,常见的原材料和零件有矩形、圆形以及不规则的形状.针对上述问题,本文主要采用针对二维规则板材下的矩形优化切割排样算法.
对于规则板材的矩形件排样问题具体数学表述如下
(1)

在矩形件排样过程中需要满足以下约束条件:1)矩形件rj排列在板材区域内;2)不同的矩形件ri和rj(i≠j)排列不能重叠;3)矩形件rj的边与板材边平行.
1.2 排样数学模型
基于上述分析,以最大限度地节省原材料为目标函数,构建优化目标,即
(2)
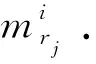
定理1式(2)中的最小化优化函数等价式(3)给出的最大化优化函数,即
(3)
证明 式(2)的优化目标等价为
(4)

(5)
于是,定理1证毕.
基于定理1,矩形件排样过程中需要满足
(6)
(7)
xi+li≤W
(8)
yi+wi≤H
(9)
xi+li≤xj∪yi+wi≤yj
(10)
xj+lj≤xi∪yj+wj≤yi
(11)
xi,j,yi,j≥0
(12)
i=j=1,2,…,m
(13)
从所构建的数学模型可知,其变量是离散不连续的,问题的解也是离散的,因此矩形件排样问题是约束离散优化问题.一方面,由于该问题是非线性的,传统的解析法无法求解.同时由于排样问题是NP完全问题,这类问题在理论上存在一种算法可求得最优解,但求解时间随着问题规模的增长呈指数关系增加,在生产实际中过长的求解时间是不可接受的.因此,本文提出一种基于启发式的板材排样优化算法,通过剪枝优化,在提高板材利用率的同时,缩短时间,提高求解问题的效率.
2 启发式板材排样优化算法
2.1 基本思想
针对矩形件排样,假定每次排样总是将零件排列在板材(L,W)的左下方,排样过程就是求解零件的最优排列位置,将板材和零件置于同一个二维平面,则零件的位置(x,y)可根据矩形件的长宽和排列方式确定.实际中,约定按照大件优先原则进行排样,取得尽可能大的利用率的原则进行优化排样.以3个矩形(A,B,C)为例,在排样的过程中,可看作为排样树,如图2所示.
由图2可得,3个矩形所构成的排样树分支数已经很多,在实际的工业大规模生产中,工件种类多、数量大,构成的排列树的分支数会急剧增加,属于计算复杂性较高的一类NP完全问题,随着零件的增加解的数量成指数倍数增长,因此确定性算法在庞大的解空间中寻找最优解的时间会急剧增加,达到让人不可接受的程度.为了满足生产需要,高效的求解矩形件排样问题,并使排样结果尽可能接近最优,本文提出了一种基于启发式的板材排样优化算法,其是在状态空间中的搜索对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到最终目标.这样可以省略大量无谓的搜索路径,提高了效率.
2.2 评价函数
评价函数是启发式算法剪枝优化的重要依据,关系到算法求解问题的效率,其设计取决于所要求解的优化问题本身.评价函数利用当前与问题有关的信息指导搜索过程,在排样搜索过程中,通过比较评价函数值大小,决定要扩展的下一个待排矩形件,省略大量无谓的矩形件试排搜索路径,以免盲目地扩展搜索,从而加快排样速度.针对板材排样问题,给出了如下的评价函数
(14)
式中:ηrj表示当前零件rj在板材上的利用率;γrj表示当前零件rj的紧密度;srj为当前零件面积;W为可行域面积,可行域指的是待排矩形件在当前布局空间所有可行位置的集合.
式(14)中定义了紧密度指标γ,用于衡量量化零件之间的紧密程度.若紧密度越大,则这样的启发式放置将有效排列邻接各物体,使得排样中的未利用空隙越小,即容器的面积利用率越高.本文紧密度定义为当前零件与已排零件之间的关系.
假设已经排列好的零件个数为k,放置新的零件时,总是从已经排好的零件出发,使新排列的零件与已排列的零件具有紧密关系.假设当前待排零件rj的中心点为(xj,yj),已排零件的中心点为(xci,yci),则中心点欧式距离为
台式高速冷冻离心机SG3-18K购于Sigma公司;5424R高速冷冻离心机购于德国 Eppendorf公司;CFX96 Deep Well Real-time System、QX200 Droplet dPCR系统购于美国Bio-rad公司;Tissue Lyser II组织研磨仪、QIAxpert核酸浓度检测仪购于德国 Qiagen公司。
在选择排样放置位置时,选取最小欧式距离的零件,即当前零件与已经排列好的零件之间的距离为d=min (d1,d2,…,dk).如图3所示,求当前零件rj与已排零件B之间的距离.当零件rj横放时,紧贴零件B,中心距离为d1;当零件rj竖放时,中心距离为d1′.
依次类推,求出当前待排零件与所有已排零件的距离,比较得出最小值d,记录紧贴零件ri,记录rj的摆放位置是横放或竖放.距离越小,说明零件之间的紧密度越大,则紧密度记为γrj=1/d.
2.3 算法流程
在矩形件优化排样中,矩形件的排放顺序和排放方式,影响着板材的利用率.
2.3.1 排样矩形件定序
待排矩形件的排放顺序(矩形件定序)是每种排样算法不可避免考虑的问题.在排样研究中,部分算法通常考虑矩形件自身属性特征,比如面积大小、长宽比等.根据式(14)给出的评价函数,提出的算法对尚未排样的矩形件在矩形空间的利用价值进行评价,找到其中最大的评价函数值Fj=max (Fi,i=1,…,m),则rj作为当前待排的矩形件.
2.3.2 排样矩形件定位
确定待排矩形件的排放顺序后,优化当前待排零件在布局空间中的摆放位置.根据2.2节提到的紧密度策略,得出:
1)计算紧密度值最大放置矩形件,如存在多个零件与该零件的紧密度值最大,则进行下一步骤;
2)比较多个零件的中心坐标值(xcj,ycj),若xck 2.3.3 算法主要步骤 算法的主要步骤如图4所示. 算法采用1.2节给出的板材排样模型,采用 Hopper 和Turton给出的C1~C5组公开案例[12],同时另定义一组测试案例C6,板材大小为2 000 cm1 500 cm,所用矩形件规格和数量分别为:90 cm120 cm, 30;150 cm100 cm,30;280 cm120 cm,28;150 cm250 cm,20;60 cm50 cm,10;50 cm150 cm,5;180 cm220 cm,4;55 cm80 cm,4. 为验证本文算法的有效性,将其与贪婪算法、模拟退火算法在相同的案例数据下分别进行比较.贪婪算法因其算法简单,在最初研究排样时广泛应用,其基本思路是从问题的某个初始可行解出发,逐步向目标函数靠拢.模拟退火算法为当前解决问题中常用的智能算法,是解决组合优化问题的随机搜索技术,不断对当前解迭代,从而达到使目标函数最优. 模拟退火算法设置迭代次数为200,温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一,虽T值越大性能越高,但速度也越慢,通常设置初始温度T=1 000、终止条件T<1,衰减函数T′=0.9T.使用Matlab搭建了实验环境进行了仿真实验,针对实验结果进行算法性能分析. 3.2.1 板材利用率分析 表1中给出3种算法在测试案例数据下的板材利用率,所用板材数以及算法运行时间的情况.由表1中数据可得,在案例数据C1和C2中,本文算法得板材利用率虽不是最优,但随着矩形件数量及种类的增加,本文算法相比于另外两种算法都有较大的提高,因此,本文提出的启发式优化算法表现出较强的全局寻优能力. 表1 不同算法性能比较 图5为测试案例C6下3种算法的排样结果.从图5中可以看出本文算法排样结果相对规整,产生的空隙废料少,具有较好的排样效果. 3.2.2 时间复杂度分析 根据表1可知,不同算法耗时情况随着矩形件数量的增加,本文算法排样时间仍保持较低增长且耗时远低于模拟退火算法,而模拟退火算法耗时急剧上升.另外,由于模拟退火算法中通过退火温度控制着求解过程向最小值的优化方向进行,通常情况下,为了能够使求解的值接近全局最优解,退火速度会设置较小值,则增加了运算规模.因此在大规模工业生产中,会耗费大量时间,不符合实际生产需求. 1)本文提出的启发式板材排样优化算法,主要是利用问题本身的信息作为启发式的搜索信息,通过分析零件之间的紧密度及利用率,设计评价函数.在排样过程中,通过比较评价函数值的大小,可进行剪枝,在提高利用率的同时,缩短时间. 2)实验结果表明所提方案的有效性和可行性,符合现代大规模工业生产的需求. 本算法还可以进一步研究,比如考虑板材为不规则板材以及裁剪的零件为多边形零件或不规则零件,使研究方案更加符合生产需求,寻找合理的方法解决后续的问题.3 实验验证及算法性能分析
3.1 实验环境及参数设置
3.2 算法性能分析

4 结论

