基于知识点决策树的学生学习成绩预测研究

王小越 吴筱萌

摘 要：传统教学中教师无法及时关注每个学生的知识掌握情况，对学生学习状况有更深入的了解，学生也无法准确對自己学习过程中出现的症状进行及时诊断。本研究以七年级数学为例，尝试进行学生数学知识点掌握程度的分析，并基于数学知识点掌握程度和成绩等级数据，采用决策树C5.0算法构建学习成绩预测模型并验证了模型的有效性。这对教师的教和学生的学，以及后续开展关于知识点和学习成绩的研究都有一定参考意义。

关键词：决策树;数学知识点;预测模型

中图分类号：G434文献标志码：A文章编号：2096-0069（2020）05-0070-05

收稿日期：2020-03-27

作者简介：王小越（1992— ），女，河北唐山人，助教，硕士，研究方向为学习科学与技术、学习分析、信息技术教育等;吴筱萌（1966— ），女，北京人，副教授，博士生导师，研究方向为网络远程教育、信息技术的教学应用、课程教学与教师发展、信息技术教育研究等。

引言

《中国教育现代化2035》明确提出要“利用现代技术加快推动培养模式改革，实现规模化教育与个性化培养的有机结合”[1]。其有机结合的基础在于，计算机能够掌握不同学习者的不同特征，并进行分析、预测，给出适当建议。

传统教学中，教师对学生学习情况的掌握仍然只能凭借书面测验和印象进行大概评估，缺乏精准性和科学性，无法深入地了解每个学生的学习状况以及对特定知识的掌握情况，为学生提供个性化指导和教学。学生无法通过作业、考试成绩等准确地判断自己是否真正学会并运用特定知识或概念解决实际问题，不能全面了解自己学科知识的掌握情况。在这样的背景下，本文以七年级数学为例，以为学生提供个性化学习分析和预测学习状态为目标，尝试依据学生平时作业和测试成绩相关数据进行学生数学知识点掌握程度的分析，并基于七年级数学知识点掌握程度数据，采用决策树C5.0算法构建了数学学习成绩预测模型，并检验模型的有效性。

一、研究基础概述

（一）知识点及掌握程度相关研究

周越、徐继红在结合了学习研究的主要经典理论、现代心理学的知识观以及其他学者的观点后，认为在课程内容体系中，能够与教学目标进行直接对应的单一命题就是知识点[2]。关于知识点掌握程度的分析，已有研究主要采用以下方法：

（1）知识点正确率[3];

（2）习题得分率[4];

（3）相似性度量[5];

（4）认知诊断模型中的DINA模型的EM算法[6];

（5）利用“试题-知识点-应答情况”表对学生数学知识点状态进行表征，来确定掌握和未掌握的知识点[7]。

（二）决策树算法

决策树算法C5.0是学习分析领域使用最广、最流行的分类预测技术之一。相较于其他学习分析算法，决策树算法C5.0的优点如下：（1）可以处理连续型的高维数据，可按照目标类别进行数据分类。（2）能够产生易于理解的知识，形成的预测模型可解释性强。（3）工作效率较高，且通常情况下会具有较高的正确率，为用户提供可信度较高的信息。决策树算法C5.0的主要内容如下：

设S是训练样本集，s为样本个数。假定样本集S中目标变量可取m个不同值，则样本集S中具有m个不同的样本子集Ci（i=1，2，…，m），si为样本子集Ci在S中的个数，样本集S所期望的信息熵为：

若某个属性A有v个不同值，则属性A可将样本集S划分为v个样本子集（S1，S2，…，Sv），|Sj|为样本子集Sj的个数，则属性A 实际所需的信息熵为：

属性A的信息熵越小，表明该属性对样本集S划分的纯度越高。则属性A的信息增益（样本集S原来所需的信息熵与利用属性A进行划分后所需的信息熵之差）为：

如果以属性A具有的值作为基准对样本集S 进行划分，其初始的信息量为：

那么属性A 的信息增益率（信息增益与初始信息量之比）为：

C5.0算法就是通过不断选择信息增益率最大的属性来作为决策节点，进行决策树的构造。

本研究中七年级数学知识点较多，要处理这种知识点过多的高维度属性特征的数据集，并按照特定的目标成绩类别进行数据分类、构建可解释的学习成绩预测模型，需要采用决策树算法C5.0进行实现。

二、样本选择及数据预处理

本研究采用了2017年常州市某中学七年级的6套在线暑假数学作业作为数据来源。6套暑假数学作业由该校老师编制。每套作业共30题。每套作业完成人数分别为1142人、979人、926人、858人、829人、814人。通过数据核查处理后，最终筛选出752人的做答数据。

假期作业一般是一个学期知识学习的总结与复习，本研究假设此6套数学作业中的知识点汇总基本代表了七年级数学下学期知识点的总体。本研究邀请到常州市某数学教研员，对试卷的知识点进行了标注，共65个知识点。

三、知识点掌握程度计算及学习成绩预测模型构建分析

（一）知识点掌握程度计算

数学知识点掌握程度的计算是学习成绩预测模型构建的基础。数学知识点掌握程度的计算主要存在两个难点：一是知识点对错如何确定，二是针对知识点应该采取怎样的计算方式来分析掌握程度。

本研究中常州市某中学七年级6套暑假数学作业中的试题均为单选题，考查的知识点可能包含一个或多个，大体可分为四类，试题类型及相关说明如表1所示。

考虑到考查多个知识点试题类型的多样性，并且无法直接判断学生到底掌握哪个知识点，未掌握哪个知识点，本研究将知识点掌握对错评定的标准定为：题目答对则该题目对应的一个或多个知识点掌握，题目答错则该题目对应的一个或多个知识点未掌握。

如前所述，已有研究中关于数学知识点掌握程度的分析中多采用计算知识点正确率的方法、计算得分率的算法或相似性度量方法。针对本数据样本，这些计算方法存在一定的问题。例如，计算得分率算法将题目分值作为一个重要变量，分值的高低往往代表了试题的难度或不同的考查能力，比如分值越高表明题目本身越难或考查了知识点综合运用能力。但本研究中的作业试题分值一样，无法体现题目分值的意义，丧失了分值在知识点掌握程度分析时的重要作用。相似性度量方法主要是在学生没有学习某些知识点时，根据该学生已学习的知识点情况，在其他将所有知识点都学完的学生中找出与该学生已学习知识点情况最相似的一个人，然后通过计算来估算出该学生对未学习知识点的掌握程度，本研究数据中的知识点都是学生学完的，所以此方法对本研究知识点掌握程度的计算也不太适用。

为此，本研究对知识点掌握程度的计算方法是统计知识点的正确率，即每个知识点的掌握程度等于该知识点被正确答对的个数除以該知识点出现的总个数，每个学生的每个知识点的掌握程度的值介于0～1之间，数值越接近于1表明学生对该知识点掌握得越好，反之，越差。

决策树的目标属性为分类类型，需要对学生成绩进行离散化处理。每套作业满分为100分，设90～100分为A、80～89分为B、70～79分为C、60～69分为D、59分及以下为E。将学生6套作业的得分累计求和，并对成绩按百分制的固定区间法的六倍进行成绩等级离散处理，即540～600分为A、480～539分为B、420～479分为C、360～419分为D、359分及以下为E。

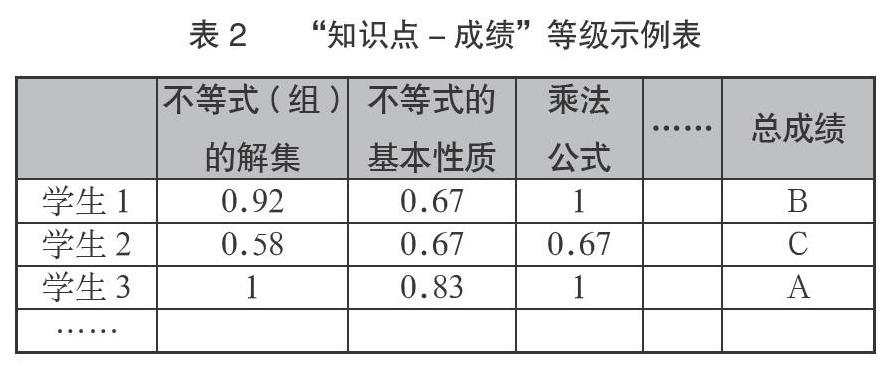
通过在Visual Studio 2010中编写公式算法程序，计算出每个学生对知识点的掌握程度，以及对学生的成绩等级属性构造后，生成了学生的“知识点-成绩”等级表，其数据格式举例如表2所示。

（二）学习成绩预测模型构建分析

本研究采用IBM SPSS Modeler 18.0软件C5.0技术进行成绩预测模型的适应性参数的决策树拟合。根据表2数据，以65个知识点掌握程度的0～1之间的连续值作为输入变量X，成绩等级作为输出变量Y，基于Pearson分布，找出非重要的预测属性2个，最后进入模型构建的知识点共有63个。

经过预测属性筛选后，采用交叉验证方法，折叠10次。该方法常被用于评估模型预测的效果，以80%的知识点掌握程度数据作为训练集，以20%的知识点掌握程度数据作为测试集。运行后，构建了具有35条规则的决策树模型，其中对应成绩等级A的规则有2条，对应成绩等级B的规则有13条，对应成绩等级C的规则有10条，对应成绩等级D的规则有6条，对应成绩等级E的规则有4条。考虑到规则较多，本文以对应成绩等级A的规则集为例进行呈现，如图1。

决策树规则集结果显示，成绩等级A对应的规则1中有11个样本数据符合规则，其中81.8%被正确预测;成绩等级A对应的规则2中有74个样本数据符合规则，其中87.8%被正确预测。35条决策树规则集显示，规则集中共包括610个样本数据（占总样本的81.8%），预测成绩等级A、B、C、D、E的人数分别为85、218、97、63和147人。在63个知识点中，只有“代入消元法解二元一次方程组”“三角形的内角和”“不等式的基本性质”等19个知识点掌握程度进入模型，说明在这63个知识点中此19个知识点对学生的学习成绩有较大影响。在19个知识点中，“代入消元法解二元一次方程组”在35条规则集中均有出现，是决策树第一个最佳决策节点，表明该知识点的掌握程度对学生的学习成绩具有更大的影响。以该知识点掌握程度值0.62为临界值，知识点掌握程度大于0.62的学生成绩等级为A、B、C、D、E的人数分别为85、211、80、16和5人，说明学生对该知识点掌握程度超过0.62时成绩等级最大可能为B，其次是A。所以，学生需在教师进一步讲解以及自己深入理解该知识点解题方法的同时，不断练习该知识点的相关题目以掌握解题方法，将该知识点的掌握程度提升到0.62以上才有可能提升学习成绩。除“代入消元法解二元一次方程组”外，其他18个知识点及其重要性排序依次为不等式（组）的解集、三角形的内角和、不等式的基本性质、真命题与假命题、三角形的外角、平行线的性质、整式的加减、幂的乘方与积的乘方、多项式乘多项式、有理数比较大小、二元一次方程组的应用、同位角内错角同旁内角的识别、多边形的内角和、单项式乘多项式、二元一次方程（组）的基本概念、科学记数法、中线高线角平分线、因式分解的概念。IBM SPSS Modeler 18.0软件C5.0技术中的变量重要性排序表明了知识点掌握程度对学生学习成绩的影响，重要性越高，该知识点对学生的学习成绩影响越大。

模型的有效性是检验模型是否可用的主要方法，本研究利用SPSS Modeler中的分析功能进行评估，结果显示训练集正确率为81.26%，测试集正确率为80.61%。可以看出，无论是训练集还是测试集的模型评估正确率均在80%以上，表明此模型具有较好的可行性、有效性。

四、讨论与展望

本研究以某校七年级学生暑假数学作业为数据集，对七年级下学期数学知识点掌握程度进行了计算，在此基础上，采用决策树C5.0算法构建了学习成绩预测模型——规则集。模型中训练集和测试集正确率均在80%以上，效果良好，说明该模型在实际应用中能够给出较佳的预测，这也表明可以利用决策树算法对知识点和学习成绩之间的关系进行深入挖掘。

通过该方法构建的规则集模型直观、易于理解，可以发现哪些知识点对于学生学习成绩的影响比较重要，对教师的教学有指导意义。针对学生平时的学习成绩，如果能够通过这种方法去分析知识点掌握情况并构建学习成绩预测模型，每个学生都可以准确找到自己的薄弱知识点，从而有针对性地加强薄弱知识点的学习以提高自己的学习成绩。对于中考、高考的试卷分析采用这种方法，可以帮助找到更重要的知识点，供教师和学生参考。

由于本研究所获得的学生作业数据有限，以此构建的知识点掌握情况预测学生成绩模型的适用性有待进一步提升。未来可选择一个学区的阶段性考试数据以增加数据量，通过引入知识点相关的描述性因素和多种试题类型以更精确地计算学生知识点掌握程度，提高学习成绩预测模型的可行性和拓展性。

Abstract： In traditional teaching，teachers can not pay attention to each students knowledge mastery timely and provide personalized guidance and teaching，and students also cannot diagnose their symptoms appeared in their own learning process timely and precisely.This research，taking mathematics of grade seven as an example，tries to analyze the mastery degree of math knowledge point，and，based on the mastery degree of math knowledge point and grading data of academic record，adopts decision tree C5.0 algorithm to construct prediction model of academic record，and validates the effectiveness of this model，which is of certain significance of reference to teachersteaching and studentsstudy，and also the research related to the knowledge point and academic record carried out later.

Key words： decision tree;math knowledge point;prediction model