基于观测器的线性离散系统预见重复控制

兰永红，夏君君

(湘潭大学 自动化与电子信息学院，湖南 湘潭 411105)

0 引言

在工业生产的实际应用中，存在着许多周期性的控制任务，如脉宽调制(Pulse Width Modulation, PWM)逆变器整流控制[1]、伺服驱动[2]、搬运、装配、喷涂的工业机器人以及周期性时间序列预测与控制[3]等。随着控制精度要求的不断提高，对于这类系统的研究具有重要的意义。重复控制是解决这类周期信号的跟踪与干扰抑制的有效方法。

重复控制器包含一个正反馈时滞环节，该环节利用上一周期的误差信号，使系统的输出能够无静差地跟踪系统的输入。尽管重复控制最初是在连续性系统中提出的，但是随着计算机技术的发展，工业控制过程中通常采用离散模型；此外，利用计算机来实现重复控制器可以利用其强大的数据存储与处理能力，改善系统的性能，故离散系统[4]的重复控制得到了广泛的关注[5]。实际上，重复控制器包含两个完全不同的行为：一个周期内连续控制的行为和各个周期内连续学习的行为[6]。因此，将二维模型的方法引入离散重复控制系统中更符合离散重复控制的本质[7]。文献[8]针对一类不确定线性系统，通过独立考虑重复控制系统两个完全不同的行为，提出一种离散鲁棒重复控制系统设计的二维模型方法;文献[9]针对参数不确定性的系统，提出了基于二维混合模型的改进重复控制系统的干扰抑制方法。在工业生产的实际的过程中，并不是所有被控系统的状态可直接测得。解决这一问题的方法之一是引入状态观测器，实现状态的重构。文献[10]提出一种基于二维模型的离散观测器重复控制方法，获得了对系统鲁棒稳定与渐近跟踪的线性矩阵不等式(Linear Matrix Inequality, LMI)条件。

当已知未来参考信号或干扰信号时，系统控制器的设计会利用这些信息来提高系统的控制性能，该方法即为预见控制。由于预见控制利用已知的未来目标信号与干扰信号，能够改善系统的品质，受到了许多学者的重视[11-12]。文献[13-15]阐述了预见控制方法的理论、计算以及在线性直流无刷电机、电力转换器、机械手、机床，汽车悬架装置、巡航导弹地形跟踪控制等控制系统中的应用;文献[16]将H∞控制与预见控制相结合，得到了H∞预见控制的相关结果;文献[17]针对一类线性离散时间系统，提出一种最优控制器的设计方法;文献[18]从粒子滤波角度出发，设计了一种无人机航母自动着陆的预见跟踪控制的方法。

尽管基于二维模型的离散重复控制与预见控制的研究均已取得了很多成果，但是将两者结合起来的研究并不多见。受以上文献的启发，为了提高系统的控制精度，本文提出一种基于二维模型的预见重复控制方法。考虑到被控对象的状态不可测问题，本文还将进一步研究基于观测器的预见重复控制问题。

1 预见重复控制器设计

离散重复控制系统的基本结构如图1所示。

图1中重复控制器的时域形式为：

(1)

其中：L为时滞环节的延时时间，等于参考输入信号r(k)的周期；v(k)为离散重复控制器的输出；e(k)为系统的误差信号，即

e(k)=r(k)-y(k)。

(2)

本文考虑如图2所示的预见重复控制系统设计问题。图2中CR(z)为基本重复控制器;P(z)为一类具有范数有界不确定性线性离散系统，其状态空间表达式为：

x(k+1)=(A+δA)x(k)+(B+δB)u(k),

y(k)=Cx(k)+Du(k)，

(3)

其中：x(k)∈Rn、u(k)∈Rm、y(k)∈Rq分别为控制系统的状态、被控输和系统的输出；A、B和C分别为具有相应维数的常数矩阵；δA和δB为适当维数的不确定矩阵函数，表示了系统的不确定性。假定系统的不确性具有如下形式

(4)

ΣΤΣ≤I。

(5)

图2中，Fe，Fx以及Fr(s)(s=0,…,Mr)分别为重复控制器、状态反馈控制器以及预见补偿器待定增益。易见本章提出的预见重复控制律具有如下形式：

(6)

该制器由3项组成：①基本重复控制器，用来提高周期之间的学习性能；②状态反馈控制器，用来提高每个周期内系统的稳定性；③预见控制器，利用未来目标值进行前馈补偿，以提高闭环系统的跟踪性能。

本文的设计目的是设计如式(6)的预见重复控制器，并给出控制器参数的具体求解方法，使系统能够渐近稳定，并且对于任意周期的参考输入，系统的输出都能够实现对输入无静差的跟踪，即

(7)

对目标信号r(k)作如下假设：

假设1设目标信号r(k)周期为L，且其可预见步数为Mr(Mr小于L)，即在当前时刻k，目标信号的当前值和Mr步未来值，r(k)、r(k+1)、…、r(k+Mr)为已知。

假设1是关于目标信号的预见性的假设。值得注意的是，预见信号对控制系统的性能仅在有限步内有显著的影响，当距离当前时刻较远时，对系统的影响不大[11,15]。普通的控制系统不利用可预见目标信号，相当于取预见步数为零。

对系统各个变量，进行如下的定义：

Δx(k)=x(k)-x(k-L),

Δy(k)=y(k)-y(k-L),

Δu(k)=u(k)-u(k-L),

Δr(k)=r(k)-r(k-L)。

(8)

将上式代入线性离散系统(3)中，得到如下L阶差分系统

Δx(k+1)=(A+δA)Δx(k)+(B+δB)Δu(k),

Δy(k)=CΔx(k)+DΔu(k)。

(9)

为了将目标信号已知的未来信息引入线性离散差分系统(9)，对参考信号进行提升操作。令

由假设1可知，目标信号在(k+Mr+1)时刻之后不可预见，故Δr(k+Mr+1)=0。从而可得

xr(k+1)=Arxr(k)。

(10)

结合线性离散差分系统(9)与(10)，得

(11)

其中：

根据式(4)，不确定性矩阵可以表示为

(12)

其中

此外，由式(2)、和式(9)～式(11)，

e(k)=Δr(k)-CΔx(k)-DΔu(k)+e(k-L)

(13)

令Fr=[Fr(0)Fr(1)…Fr(Mr)],由式(1)、式(6)及xr(k)定义，式(6)可以重写为

=Fee(k-L)+FxΔx(k)+Frxr(k)

(14)

重复控制依赖于两个独立的行为，即一个周期之内的控制过程和控制周期之间的学习过程。借鉴文献[6,8-10],用两个变量i,j分别来表示重复学习变量和时间变量。对于变量ζ(k)，ζ∈{x,y,u,e,r}，令

ζ(k)=ζ(iL+j)=ζ(i,j),

(15)

进一步定义

Δζ(i,j)=ζ(i,j)-ζ(i-1,j)。

(16)

根据式(16)，式(11)、式(13)、式(14)可以分别改写为

(17)

(18)

(19)

联立式(17)与式(18)，可得如下二维离散系统：

(20)

式(19)可重写为

(21)

将式(21)代入式(20)，可得

(22)

令

根据式(12)，可以得到

(23)

其中：

将式(22)重新写为

(24)

其中：

可见，线性离散系统(3)的预见重复控制设计问题可以转化为二维离散系统(24)的稳定性问题。下面利用二维离散系统稳定性理论，给出线性离散系统(3)具有形如式(6)的预见重复控制器存在条件和控制器参数求解方法。

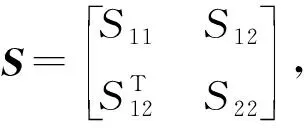
(1)S<0;

引理2[20]给定的适当维数的矩阵Y、U、W，其中Y是对称的，则Y+UVM+(UVM)Τ<0对所有满足VΤV≤I的矩阵V成立，当且仅当存在常数ε>0，使得Y+εUUT+ε-1WTW<0。

引理3[21]对于如下的二维系统

(25)

如果存在对称正定矩阵P,Q使得

(26)

则二维离散系统(25)渐近稳定，其中：

定理1对于二维离散系统(24)，若假设1成立，如果存在常数ε>0，对称正定矩阵Y,Z以及合适维数矩阵N，使LMI

(27)

则二维离散系统(24)渐近稳定，且K=NY-1。

证明根据引理1，引理3中不等式(26)等价于

(28)

(29)

将式(29)两边同时乘以diag{P-1,P-1,P-1}，并令Y=P-1,Z=P-1QP-1,N=KP-1，则有

(30)

令

上述不等式(30)等价于

(31)

根据引理2，对于所有满足式(5)的矩阵Σ，不等式(31)等价于式(32)，其中ε>0。对式(32)应用引理1，即可得式(27)，证毕。

ε-1[G1Y+G2N0 0]Τ[G1Y+G2N0 0]<0。

(32)

推论1对于线性离散系统(3)，若假设1成立，如果存在常数ε>0，对称正定矩阵Y,Z以及合适维数矩阵N，使LMI(27)成立，则线性离散系统(3)在预见重复控制器(6)作用下渐近稳定，且

[FxFr(0)Fr(1)…Fr(Mr)Fe]=NY-1。

推论1给出了线性离散系统(3)基于LMI的预见重复控制器设计方法，但预见步数的选取仍然是一个值得深入研究的问题。文献[22]提出一种可行的参考方法，即利用性能指标函数值的变化来选取合适的预见步数。具体地，可以定义性能指标

然后给定对比度ξ(一般取0.001)，如果J(Mr+1)-J(Mr)<ξ，则取预见步数为Mr。

2 基于状态观测器的预见重复控制器设计

考虑到控制系统的状态不可测，本章引入状态观测器，对不可测系统状态变量进行重构，给出线性离散系统(3)基于观测器的预见重复控制器设计方法。

对线性离散系统(3)，构造如下形式的状态观测器

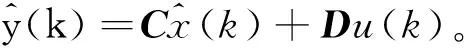
(33)

其中Lo为观测器待定增益矩阵。

基于观测器的预见重复控制系统结构框图如图3所示。易见，本章提出的基于观测器的预见重复控制器具有如下形式：

(34)

式(32)和式(34)的二维形式分别为

(35)

(36)

eo(i,j+1)=(A+δA-LoC)eo(i,j)+

(37)

根据式(4)，可得

其中

同样，系统误差方程可写为

e(i,j)=e(i-1,j)+Δr(i,j)-CΔx(i,j)-

DΔu(i,j)

-DΔu(i,j)

(38)

另一方面，由式(36)，可得

(39)

令For=[For(0)For(1)…For(Mr)]，则

(40)

其中Kox=[Fox0For];Koe=Foe。

因此，基于状态观测器的预见重复器设计问题可以转化为如下二维离散系统

(41)

在状态反馈控制器(40)作用下的稳定性问题。

将式(40)代入式(41)，有

(42)

其中：

任意矩阵Π有结构奇异值分解

Π=U[S0]VΤ，

(43)

式中：S为半正定矩阵;U、V为酉矩阵。

(44)

其中：V同式(43)中Π的奇异值分解酉矩阵;X11∈Rp×p;X22∈R(n-p)×(n-p)。

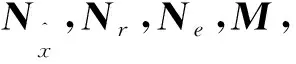
(45)

其中：

Y=diag{Y1,Y2,Y3,Y4}，

Z=diag{Z1,Z2,Z3,Z4},

则二维离散系统(42)渐近稳定，且

(46)

(47)

证明类似定理1的证明过程，如果

(48)

其中：

则二维离散系统(42)渐近稳定。注意到：

(49)

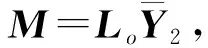
推论2若假设1成立且线性离散系统(3)具有形如(32)的状态观测器，并存在常数ε>0，对称正定矩阵Y,Z以及合适维数矩阵N，使矩阵不等式(45)成立，则线性离散系统(3)在基于观测器的预见重复控制器(33)作用下渐近稳定，且

(50)

(51)

3 数值仿真

以LX800 12V/24V永磁同步直线电机为例，电机的电磁推力方程和运动方程分别为：

系统的输出方程定义为

y(t)=[1 1]x(t)+1.50u(t)。

选取电机参数[24]：

Kf=9.60 N/A。

取采样周期T=0.01 s，可得形如式(3)的线性离散系统，且系统矩阵参数为：

C=[1 1],D=1.50。

取不确定性矩阵为：

目标信号为

取预见步数为Mr=3、Mr=10、Mr=15，应用推论1，可分别求得控制器增益。Mr=3时，Fx=[-0.648 8 -0.653 1],Fe=0.586 5，Fr=[0.610 0

0.000 4 0.000 5 0.000 5]；Mr=10时，Fx=[-0.651 1 -0.652 3],Fe=0.579 0，Fr=[0.618 8 0.000 3 0.000 5 0.000 6 0.000 6 0.000 5 0.000 5 0.000 5 0.000 6 0.000 06 0.000 06];Mr=15时，Fx=[-0.651 1 -0.650 3],Fe=0.579 9，Fr=[0.621 6 0.000 5 0.000 6 0.000 6 0.000 6 0.000 6 0.000 5 0.000 5 0.000 5 0.000 5 0.000 6 0.000 6 0.000 06 0.000 06 0.000 06 0.000 06]。

系统仿真结果如图4和图5所示。由两图可知，不同预见步数情形下，系统输出响应均能准确地跟踪目标信号，且随着预见步数的增加，系统误差最大峰值逐渐减小。

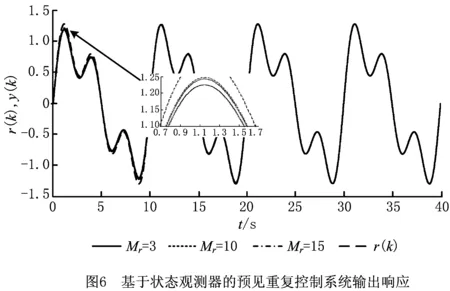
图6～图7所示为基于状态观测器的预见重复控制仿真结果。由两图可知，不同预见步数情形下，基于状态观测器的预见重复控制均能使系统输出快速跟踪系统的目标信号，且控制效果与直接实现的预见控制非常接近，显示出良好的跟踪性能。

为便于比较，图8给出了控制系统在无预见补偿的重复控制(即Mr=0，文献[8]的方法)、预见重复控制(Mr=10)以及基于状态观测器预见重复控制(Mr=10)作用下，系统的跟踪误差曲线。表1所示为上述不同控制方法下的性能比较。由图8和表1可知，引入预见补偿后，控制系统的跟踪性能明显优于无预见补偿的重复控制系统。

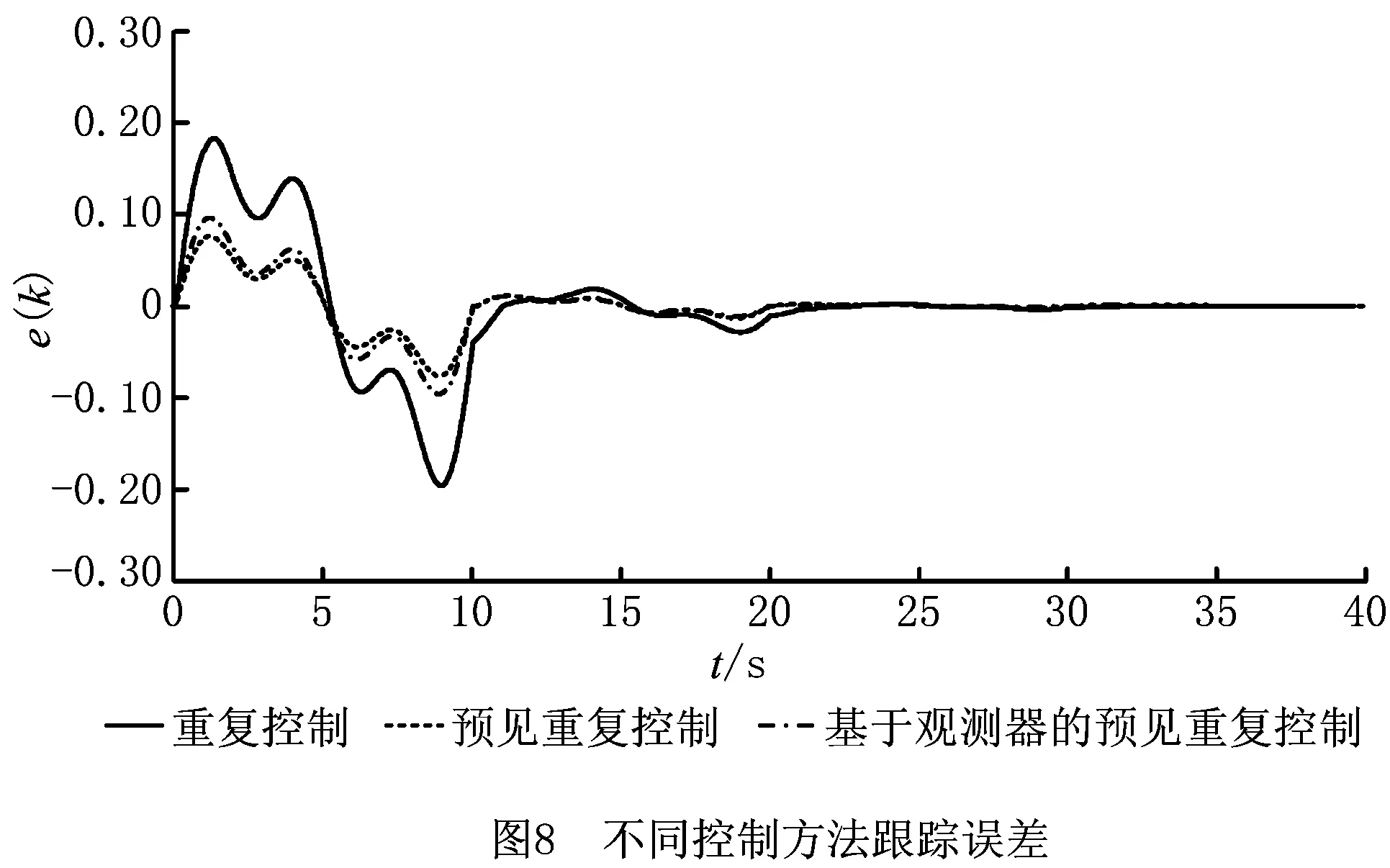
表1 不同控制方法的性能比较

4 结束语

针对一类不确定线性离散系统，本文提出一种基于二维模型的预见重复控制器的设计方法。为提高控制系统的跟踪性能，将可预见目标信号引入重复控制器，并将预见重复控制器的设计问题转化为二维离散系统的稳定性问题。基于二维离散系统稳定性理论，并借助LMI处理技巧，获得了预见重复控制器的存在条件及控制器参数求解方法。进一步，将所得结果推广至基于观测器的预见重复控制情形，通过永磁同步直线电机跟踪仿真结果，验证了所提方法的有效性。下一步，将深入研究连续系统的预见重复控制及其参数优化问题。