基于引桥动态称重的主桥应变影响线识别

李 春，杨晓燕，晋智斌，夏宏达,陈 超

(1. 中电建路桥集团有限公司,四川成都 610300; 2. 中铁大桥科学研究院有限公司,湖北武汉 430034; 3.西南交通大学,四川成都 610000)

桥梁建成使用后的健康状态越来越受到人们的关注，自20世纪80年代起发达国家陆续建立起多种桥梁健康监测系统；20世纪末21世纪初随着我国基建项目的大量实施，桥梁健康监测系统在我国开始被使用[1-3]。

相比较列车车重信息，汽车的车重与车速信息获取手段较为复杂。基于Moses算法[4]的动态称重研究已有40年的历史。王宁波研究了动态称重算法在不同形式的桥梁中的适用范围与测试精度，结果表明：跨度不大的梁板桥、肋板式梁桥等均具有较好的适用性，而箱形梁桥则存在很大局限性[5]。

本文考虑到箱梁形式的较大跨径主桥较多存在较小跨径简支梁形式的引桥这一结构特点，提出了通过在引桥上布置动态称重系统，以得到主桥上车辆荷载位置，进而反演主桥应变影响线的方法。

1 利用引桥进行荷载识别的方法

陈惟珍，通过记录钢桁架桥梁吊杆应变峰值差的方法测量车速[6]。法国路桥实验中心[7]提出无车轴检测装置(FAD or NOR)的桥梁动态称重概念，利用应变历程在车轴作用下产生的应变尖峰来识别车轴。本文利用简支梁形式的引桥作为荷载识别单元，用知间距截面的应变峰值时间差来识别通过引桥驶上主桥车辆的车速。由车速即可得到任意时刻车辆所处位置，该车辆位置信可以被用于桥梁影响线识别。

1.1 车重荷载确定

车辆荷载作为在役桥梁最重要的活荷载之一，在桥梁的各种荷载组合中占有重要地位。监测桥上移动车辆荷载，明确其分布特点对在役桥梁承载能力评估具有重要意义。

利用动应变数据进行桥梁动态称重的基本理论：

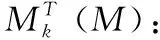
(1)

M=ESiεi

(2)

式中：N为总车轴数；Ai为第i根车轴轴重；Ik,i为k时刻第i根车轴所在位置对应的桥梁弯矩影响线坐标；E为弹性模量；εi为每片梁的梁底应变；Si为每片梁的截面模量。由式(1)、式(2)两式就建立起了动态应变与车辆轴重的关系。

1.2 荷载位置确定

在引桥上布置称重测试断面与车速识别断面，如图1所示。2#断面为动态称重断面用以识别车重信息，1#、3#断面为车速识别断面，采用应变峰值时间差来识别车速。

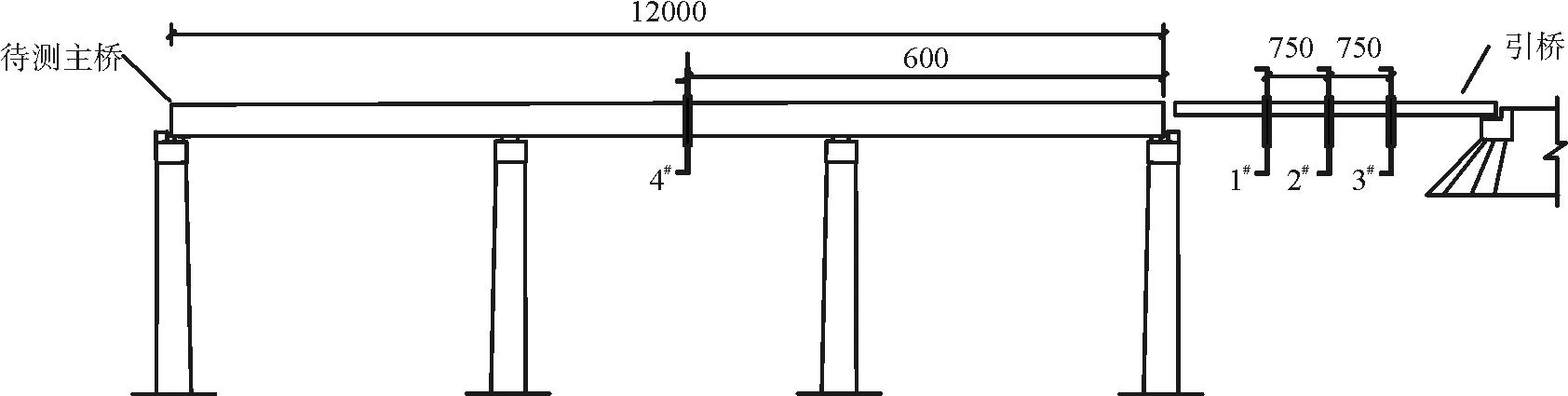
图1 测量断面布置(单位:mm)

以动应变为基础的动态称重算法如今已经较为成熟，通过该算法可得到车辆轴重数据Mi，车轴通过每个车速测量断面时应变峰值，记录应变峰值出现的时间t(Fj)，两测量断面间间隔为7.5 m，假设车轴先通过断面3#再通过断面1#，则该轴速度为：

(4)

由车速信息即可得到任意时间t车辆距离1#断面的距离，即可以此信息得到车辆在主桥上的位置(图2)。

L=t·Vi-l

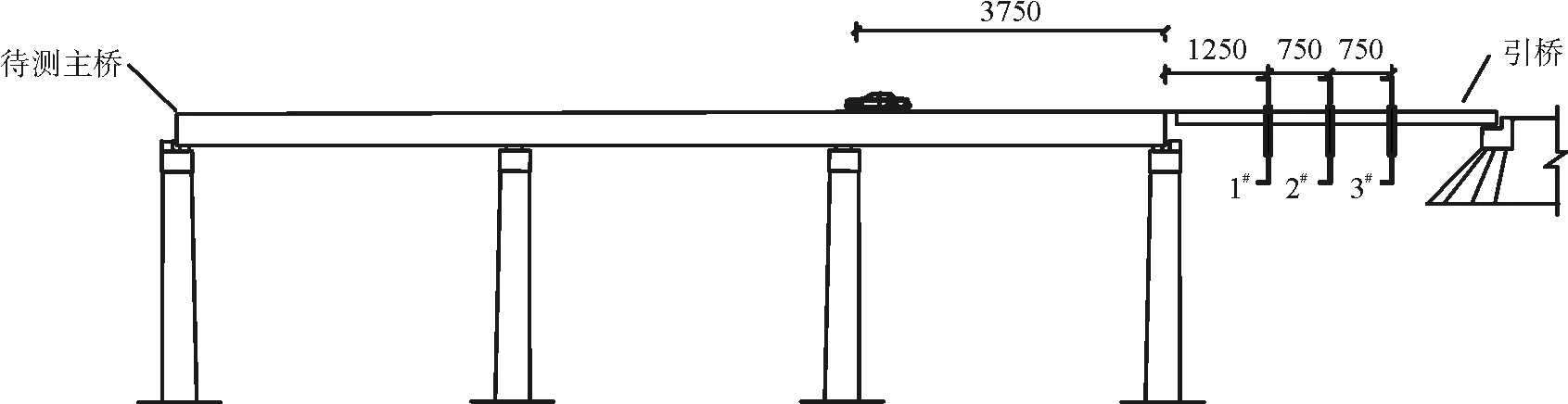
图2 车辆位置确定

由此得到车速，假定车辆在桥上正常行驶时车速不变即可在一定时间内得到通过引桥的车辆荷载分布位置。通过该位置对主桥上的车辆荷载进行重构。

2 主桥应变影响线识别

关于桥梁影响线的识别E. J. Obrien[8]，Ieng S S[9]，王宁波[10]，均采用影响线动态测试方法，通过已经预先标定车重的加载车匀速驶过待测桥梁并测量跨中应变数据，并根据加载车信息构建车辆矩阵，通过最小二乘法分离提取桥梁影响线。基本思路如下：

V·I=εr

(5)

式中:V为车辆车轴位置矩阵车辆位置矩阵，由上一章中介绍的方法利用引桥识别出的车重与车速信息进行构建；I为跨中应变影响线向量；εr为真实跨中应变向量。

实测应变时程数据为εm，但是得到的应变数据中不可避免的包括了桥梁的动力响应，直接使用此数据将导致影响线识别出现较大误差。为得到准静态的桥梁应变数据，对包含动力响应的应变数据进行滤波处理，截止频率设置为桥梁一阶竖弯振型频率。滤波前后数据变化如图3所示。

图3 时程数据对比

定义应变差：

Δε=εm-εr=εm-VI

(6)

对式(6)求导，当导数为0时，得到跨中应变影响线I的最优解。

I=(VTV)-1VTεm

(7)

2.1 算例一

使用ANSYS有限元软件进行模拟，采用C50混凝土，建立一座带有40 m简支梁引桥的3×40 m连续梁桥，模型如图4所示，计算并提取一个40 kN的移动力以10 m/s的速度通过边梁时连续梁桥中跨跨中应变时程数据，并反演连续梁桥跨中应变影响线(图5)。

图4 有限元模型

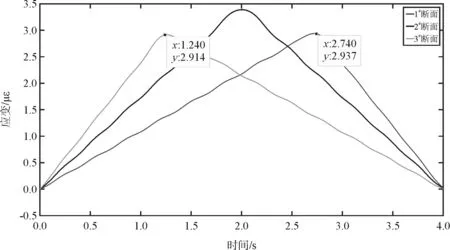
图5 引桥各截面应变时程

通过移动力通过引桥如图1所示各断面时应变时程曲线(数据已经过滤波处理)如图4并由峰值时间差确定车速，由于1#断面与3#断面间距7.5×2=15m，从图4可知时间差为1.5 s，可得速度为10 m/s与设置的车速一致。进而由车速确定该移动力驶离引桥后任一时间所处位置。

同时提取连续梁桥如图1所示4#断面梁底应变时程数据(数据已经过滤波处理)如图6，并通过式(7)反演改变影响线如图7。反演应变影响线与有限元模拟提取的影响线基本一致。

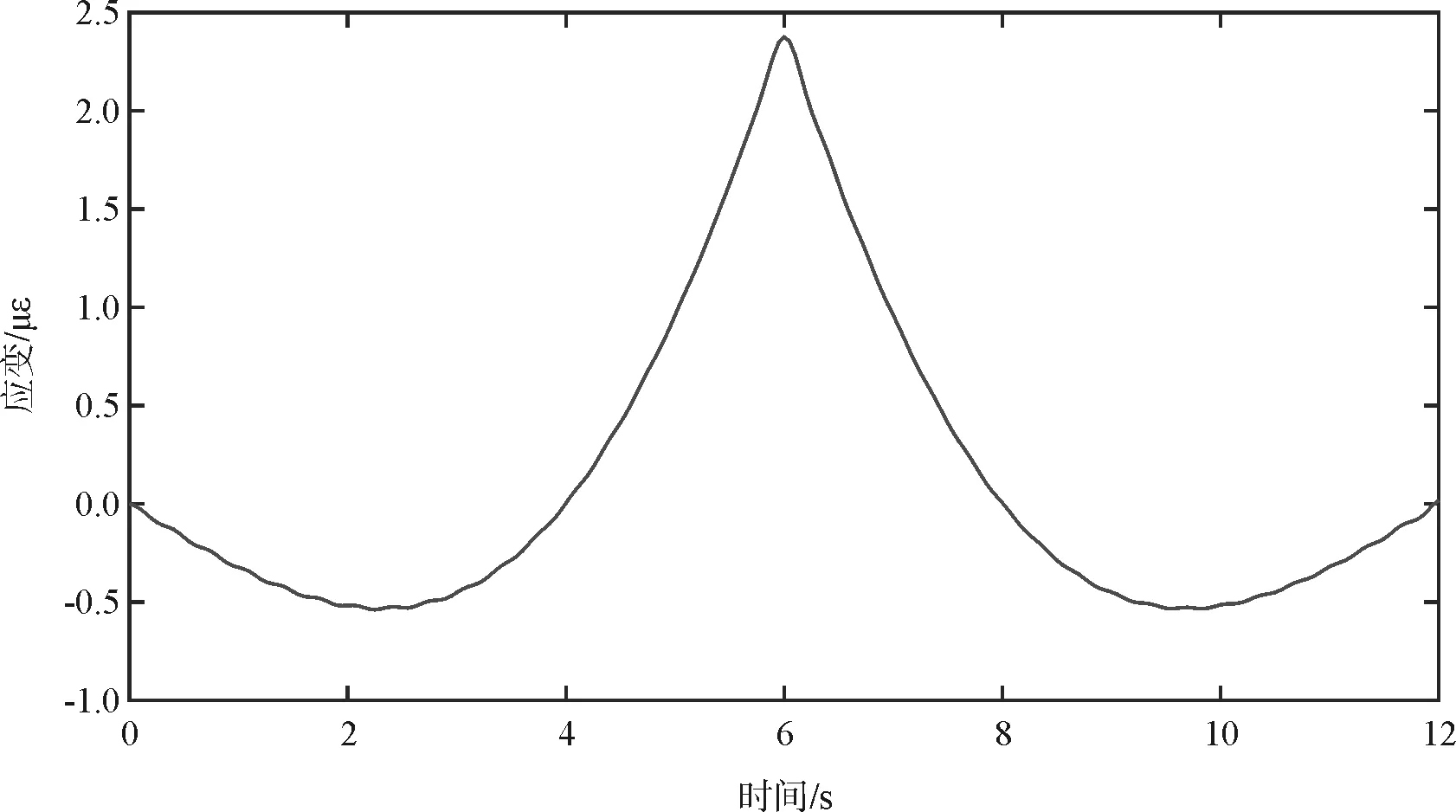
图6 连续梁桥4#断面应变时程

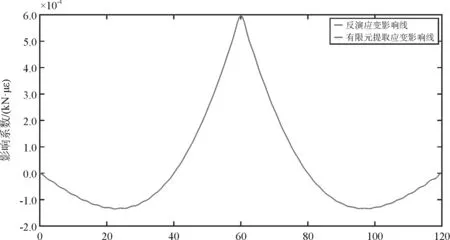
图7 断面应变影响线对比

2.2 算例二

使用ANSYS有限元软件进行模拟，采用C50混凝土，建立一座带有40 m简支梁引桥的3×40 m连续梁桥，模型如图4所示，计算并提取两个移动力(先40 kN、后80 kN)以10 m/s的速度先后通过边梁时连续梁桥中跨跨中应变时程数据，并反演连续梁桥中跨跨中应变影响线(图8、图9)。

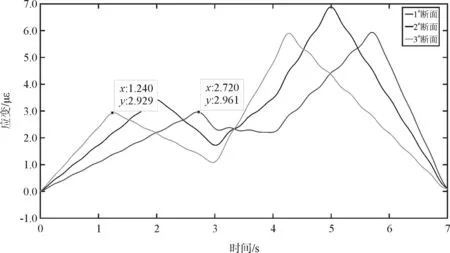
图8 荷载40kN峰值位置

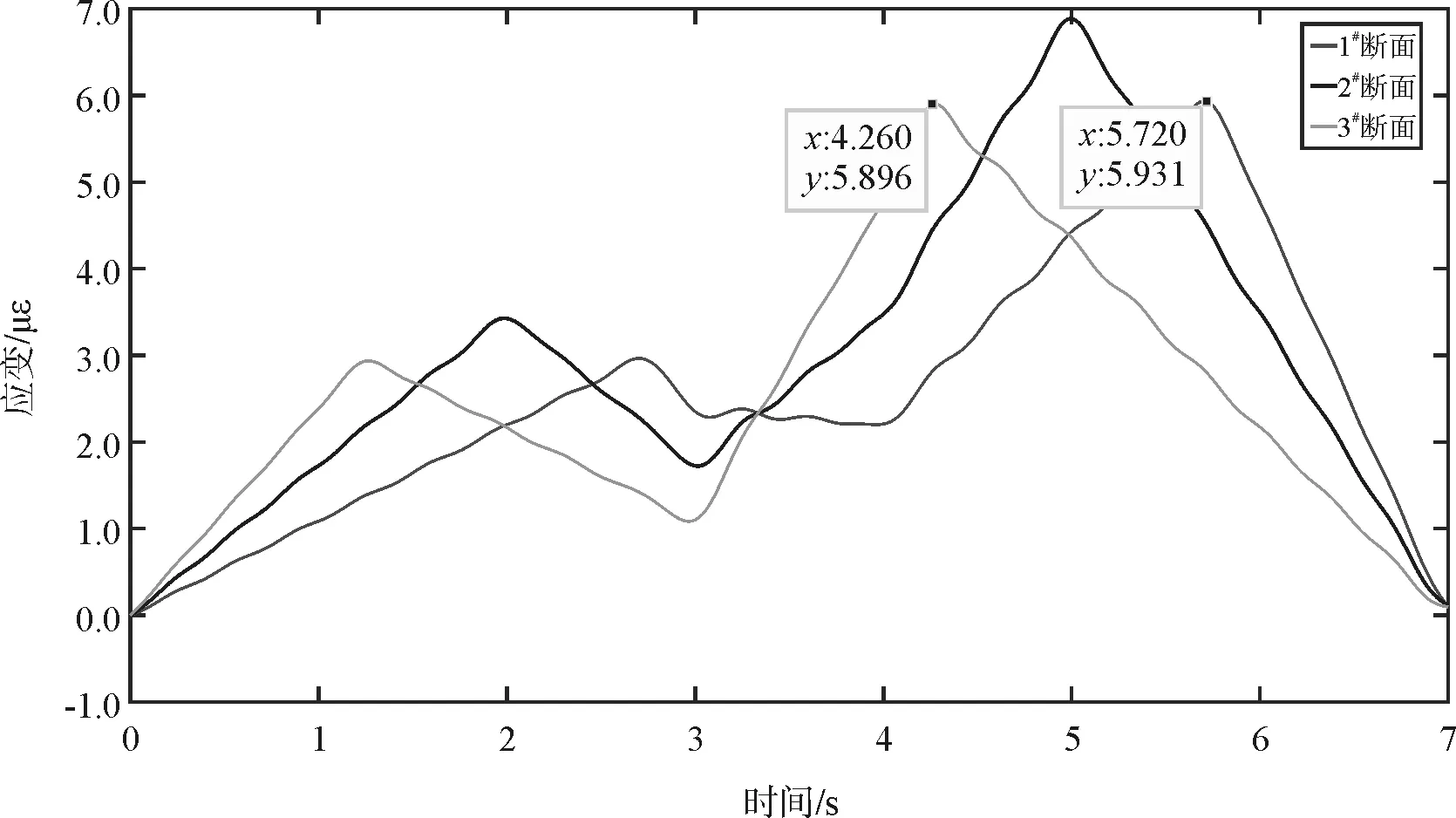
图9 荷载80kN峰值位置

由算例1中的方法，通过应变峰值时间差得到车速等数据。

同时提取连续梁桥4#断面梁底应变时程数据(数据已经过滤波处理)如图10所示，并通过式(7)反演改变影响线如图11所示，反演应变影响线与有限元模拟提取的影响线基本一致。

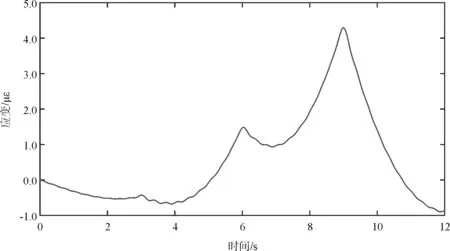
图10 连续梁桥4#断面应变时程

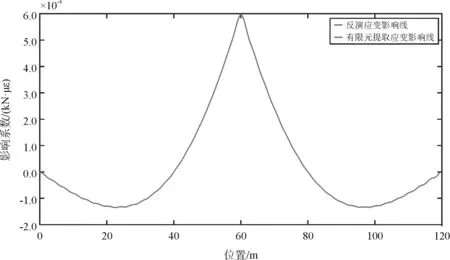
图11 断面应变影响线对比

3 实桥实测结果

四川省泸州市赤水河大桥为连续刚构桥，桥跨105 m+200 m+105 m，主桥为箱型梁。主桥配有跨径40 m，由6片钢筋混凝土T梁构成的引桥。

依托该桥的健康检测系统；其中，应变监测断面如图12所示布置。其中2#断面为引桥跨中截面1#～3#截面布置在引桥上，4#断面布置在主桥中跨跨中。引桥应变测点横桥向选取沿行车方向最右侧的一片T梁，主桥应变测点横桥向位置与引桥测点相同(图13、图14)。

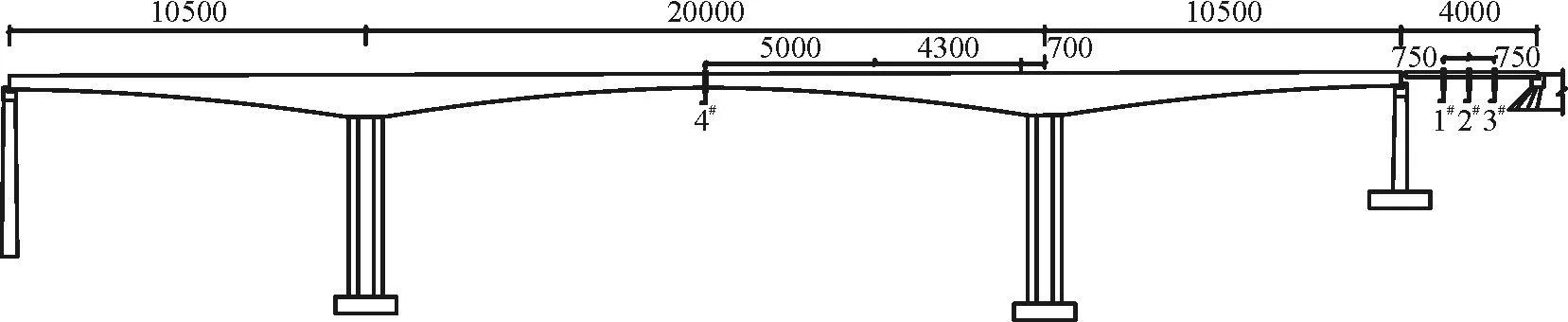
图12 测试断面布置(单位:cm)

图13 4#断面形式

图14 1#～3#断面形式

图15 实测应变

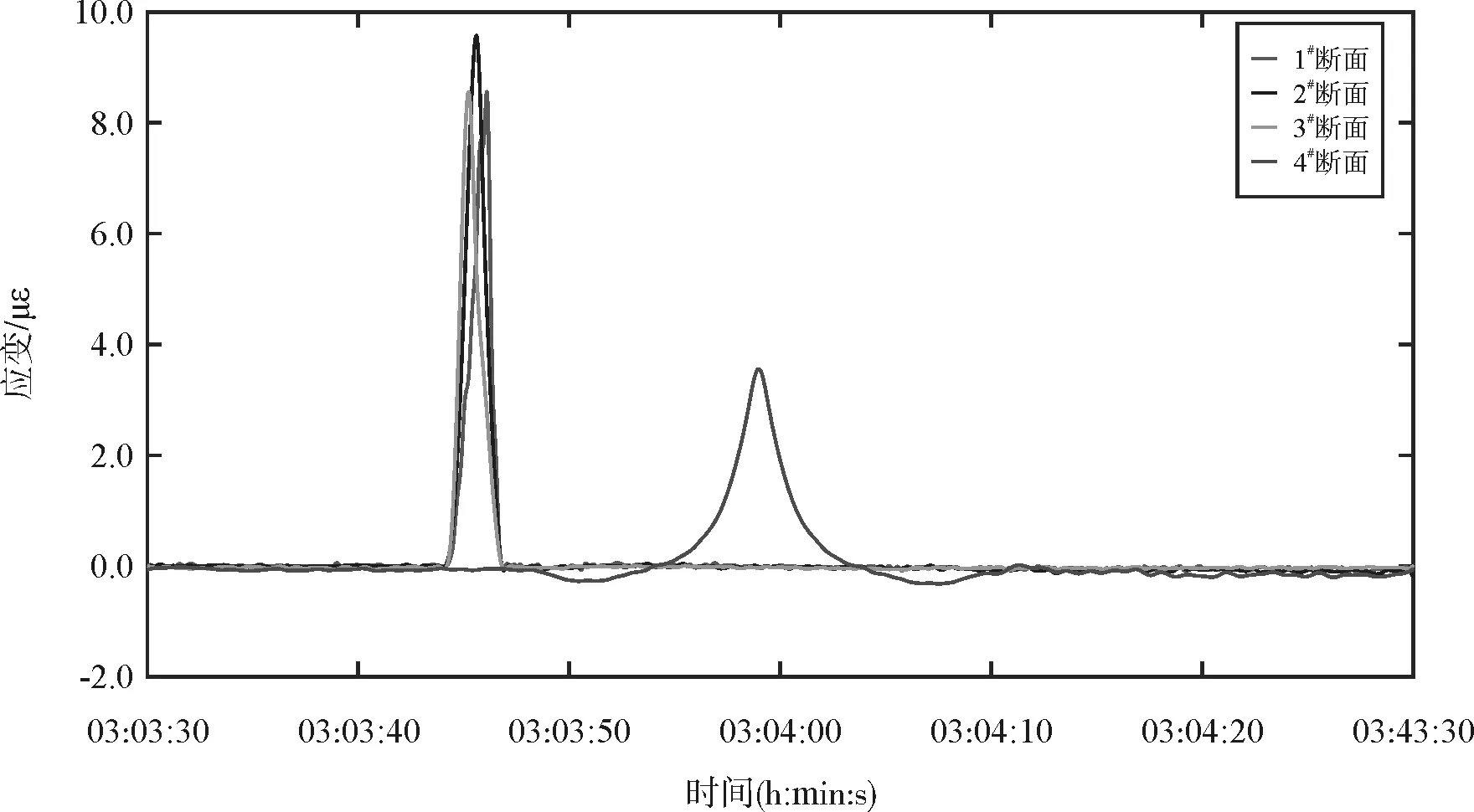
图16 截取时间应变

所选传感器对应的车道可以明显看出有五辆车通过，从数据中截取03:03:30～03:04:30时长1 min的数据为例进行主桥应变影响线识别。通过引桥进行荷载识别出的在凌晨03:03:30～03:04:30之间通过引桥驶上主桥的车辆车速为16.8 m/s，车重为270 kN。

主桥应变影响线反演结果与现场标定结果对比如图17所示。对比结果显示，通过引桥荷载识别反演的主桥跨中应变影响线与现场标定的影响线基本一致。

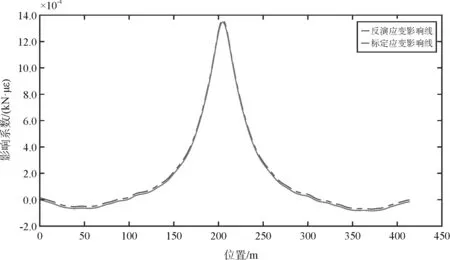
图17 应变影响线对比

4 结论

(1)有限元模拟结果显示，通过荷载经过引桥不同断面时的应变峰值时间差识别车速与BWIM动态称重相结合的方法，可以得到荷载通过引桥驶上主桥时的相对位置，以此反演得出的应变影响线与模型提取的影响线基本一致。

(2)实测结果表明，上述方法在实桥的应变影响线识别中也具有较高精度。证明了本方法的可行性。