任意截面钢筋混凝土构件容许应力法配筋数值解法

徐建华，于贞波,胡玉珠

(中铁二院工程集团有限责任公司，四川成都 610031)

随着铁路桥梁向着大跨复杂结构发展，越来越多地出现了多向受力且截面形状复杂的构件[1]。目前规范[2]只针对简单截面给出了容许应力法配筋计算公式，但对大量的非常规复杂截面，特别是不对称截面，其配筋计算难以用公式或解析方法来实现。余琪[3]对双向大偏心受压钢筋混凝土矩形截面进行了研究，从切角矩形截面的力学性质入手，运用迭代法求解了零应力线。童森林[4]针对双向受力的钢筋混凝土圆端形截面配筋计算进行了研究，通过将有效面积视作几个简单图形的组合，通过一系列变换，迭代求解了最终零应力线。杨咏漪[5]针对复杂截面复杂布筋的钢筋混凝土结构的配筋，以AutoCAD为二次开发平台，基于ObjectARX和VC++采用解析法、迭代法和图解法相结合的方式，编制相应的允许应力法任意配筋程序。

以上研究前两者针对常规截面，杨咏漪等虽然对任意面配筋问题进行了研究，但截面特性计算依靠AutoCAD，未进行理论推导，不利于直接编程。零应力线的迭代，三者采用的方法基本一致，以斜率k和与X轴交点b两个参数的二元非线性方程为目标，受初始零应力线选取影响，有不收敛现象且计算速度较慢。

本文针对铁路桥梁任意截面钢筋混凝土构件容许应力法配筋问题，在尽量简化截面前处理步骤的基础上，拟通过解析法计算截面特性，并对零应力线方程非线性求解过程进行优化，完善数值计算方法，以便于编程计算和工程应用。

1 基于格林公式的截面特性计算

钢筋混凝土截面一般由圆弧或线段围成，对非圆弧或直线部分，也可等效为多个圆弧或直线的组合，进而可将截面轮廓转换为多段线或圆弧组合的结果。假定任意钢筋混凝土截面D(图1)是由线段{Lw1,Lw2,Lw3,…Lwn}和圆弧{Cw1,Cw2,Cw3,…Cwm}为外轮廓围成的凸多边形闭合区域，其内轮廓是由线段{Ln1,Ln2,Ln3,…Lnn}和圆弧{Cn1,Cn2,Cn3,…Cnm}围成的凸多边形闭合区域。钢筋按间距和直径等效宽度为ti的条带，各条带为圆弧{Cs1,Cs2,Cs3,…Csm}或线段{Ls1,Ls2,Ls3,…Lsn}。

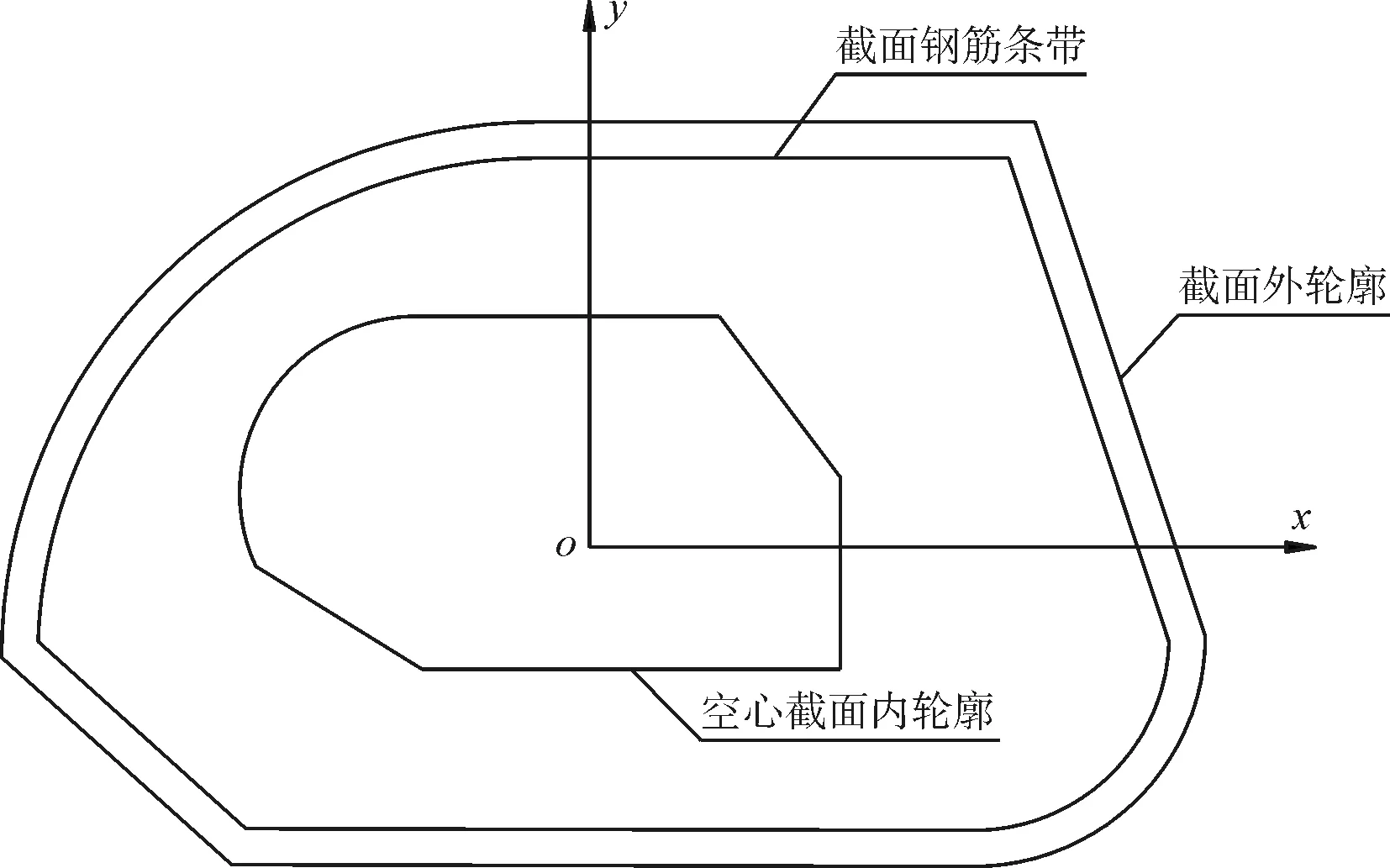
图1 任意截面D示意

在配筋计算中关注的混凝土截面特性参数如面积、惯性矩等都是二重积分，直接积分较为困难。由于截面的任意性，将截面分割成简单图形如矩形、三角形或扇形后进行计算组合也不易实现。借用格林公式[6]可将截面特性计算从面积分转换为简单的一重积分，进而实现混凝土截面特性的积分计算。以绕X轴惯性矩积分为例，见式(1)。实际工程中的混凝土构件，其截面特性总是可以表达为外轮廓截面的特性与内轮廓截面的特性之差，外轮廓截面和内轮廓截面分别是单连通区域，可以运用格林公式简化计算截面特性。

(1)

钢筋按间距和直径等效为条带，条带的宽度计算见式(2)。钢筋面积及惯性矩等参数可表达为线积分，且由于钢筋被简化为圆弧或直线条带，曲线表达式简单，容易实现。

(2)

式(2)中，d为钢筋直径，Δ为钢筋的间距。

2 截面内力的平衡状态及零应力线的确定

一般截面内力为作用于构件形心处的内力，进行配筋计算前，应将截面坐标系原点移动至截面形心处。同时，将截面坐标系进行旋转，使得坐标系X轴正方向与合弯矩方向(右手定则)一致，此时截面上内力简化为轴力N，弯矩Mx，见图2。

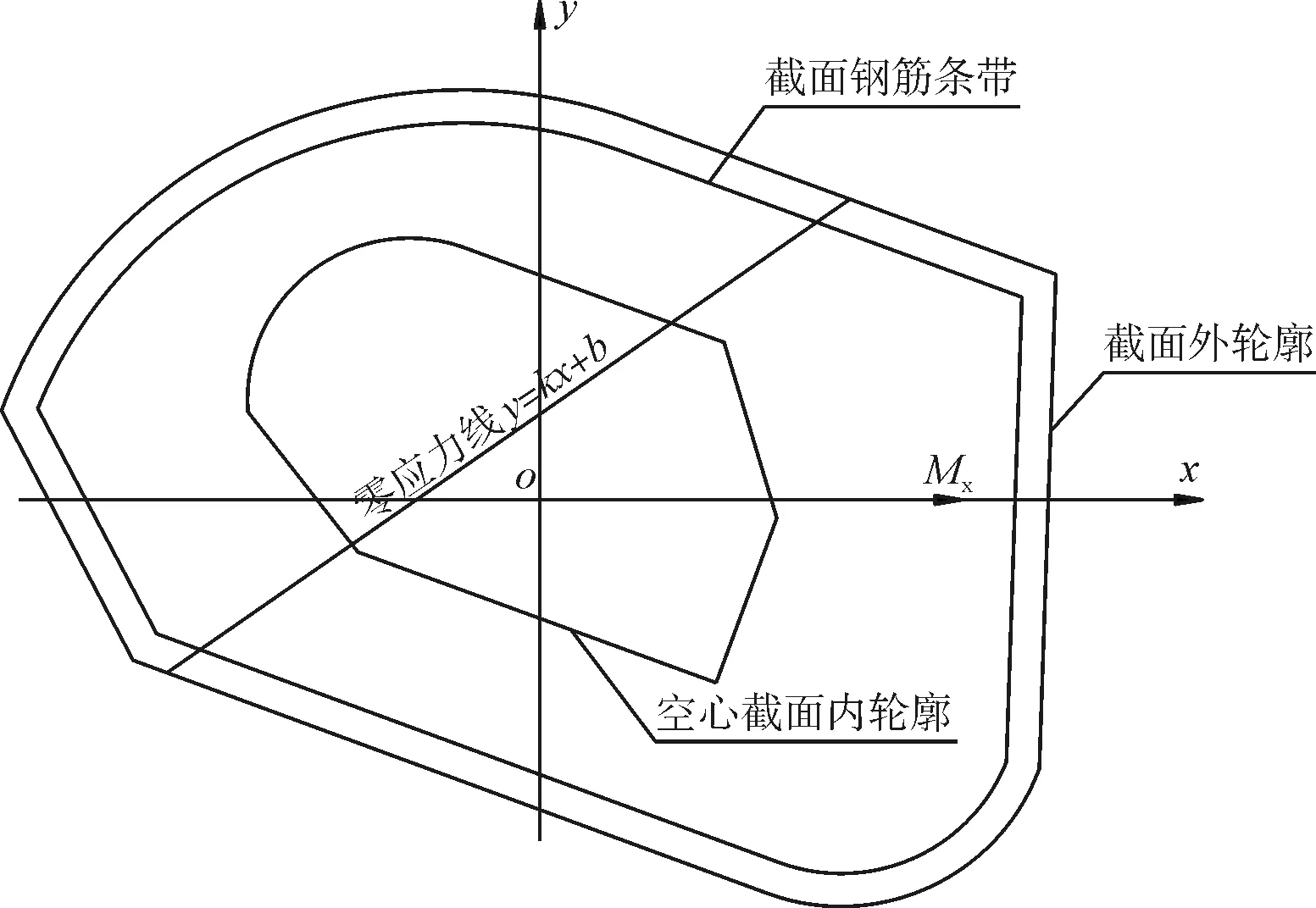
图2 形心坐标系下截面受力状态示意

假定该坐标系统为形心坐标系，则在该坐标系中零应力线方程可表达为式(3)。

y=kx-b

(3)

当截面为轴向受力构件，弯矩Mx= 0时，零应力线不存在，式(3)无解，应作为特例处理，且受力简单，可根据截面特性方便地求得应力，本文不再讨论。当弯矩Mx≠ 0时，截面零应力线总是存在；当零应力线平行于Y轴时，零应力线左右两侧合力必将形成弯矩My，截面内力不平衡，故零应力线不可能平行于Y轴，式(3)始终有解。后文仅针对弯矩Mx≠ 0的情况进行讨论。

在形心坐标系下，零应力线下方总是受压区，零应力线上方总是受拉区。零应力线分割后的截面上任意一点(x,y)到零应力线的距离为：

(4)

若h>0，则截面位于中性轴上方，是受拉区；反之位于受压区。对给定的零应力线，令受压区混凝土截面为D1，钢筋条带为S1；令受拉区混凝土截面为D2，钢筋条带为S2；混凝土弹模为Ec，钢筋弹模为Es。

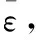
(5)

此时，受压区混凝土对原点合力为：

(6)

(7)

(8)

受压区钢筋对原点的合力为：

(9)

(10)

(11)

受拉区仅计钢筋的作用，合力计算与式(9)～式(11)类似。全截面上合力：

(12)

(13)

(14)

上式中：ND1、MyD1、MxD1为受压区混凝土合力，Ns1、Mys1、Mxs1为受压区钢筋合力，Ns2、Mys2、Mxs2为受拉区钢筋合力。A、Ixy、Ix、Iy、Sx、Sy为不考虑受拉区混凝土时换算截面对坐标系X或Y轴的截面特性。

由于My= 0，则由式(12)～式(14)有：

(15)

=(eIxy-Sy)k+(eSx-A)b

(16)

由式(15)和式(16)可知：

(17)

由式(15)可知，零应力线参数k、和b相互关联。式(17)构建起了关于零应力线参数b的一元非线性方程，可采用不动点迭代法求解，零应力线初始值选择k= 0，b= 0即可。为保证结果足够精确，可考虑采用力平衡作为迭代收敛条件，即：

(18)

式中：Ni、Mxi、Myi为第i次迭代计算得到的截面内力，N、Mx为截面内力输入值。一般情况下考虑工程设计精度取Δ=1e-3即可。相比之前研究[5]采用的以零应力线参数k或b作为收敛判定条件，由于k或b不能直接反应截面内力平衡条件偏差，所需迭代精度无法直接控制，而采用截面内力作为迭代平衡条件较为直观，方便掌控精度要求。一般迭代5～6次即可。

3 算例

根据本文方法，编写了任意截面钢筋混凝土构件容许应力法配筋计算程序(PRSC.exe)，并与相关文献计算结果进行对比。

3.1 圆端形空心截面钢筋混凝土构件双向受力计算分析

算例取自参考文献[7]，具体计算参数见表1，计算结果对比见表2。可见，本文计算方法得到的结果与参考文献结果吻合较好。本文计算中考虑了受压区钢筋位置扣除相应的混凝土面积，故计算结果略大。对一些配筋较多的高墩其截面厚度薄，纵向钢筋较多，应考虑该效应。本次计算迭代次数为5次。

表1 圆端型空心墩截面参数

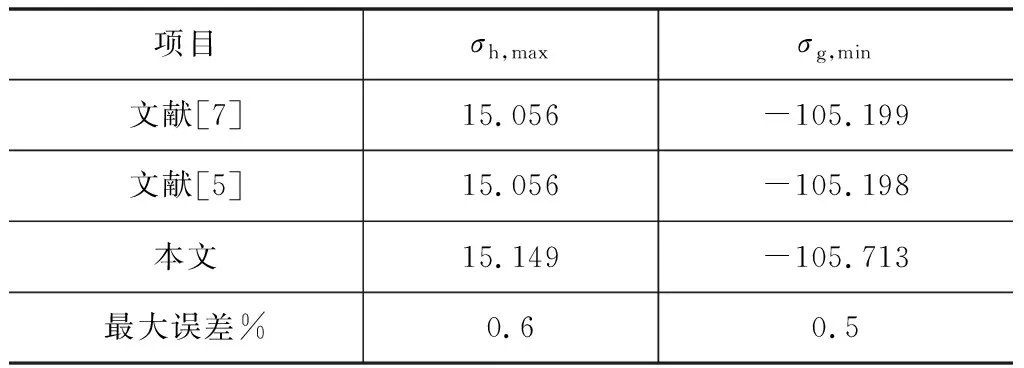
表2 计算结果对比 MPa

3.2 圆端形实体截面混凝土构件应力重分布计算分析

算例取自参考文献[7]，具体计算参数见表3，计算结果对比见表4。可见，本文计算方法得到的结果与参考文献结果吻合较好。本次计算迭代次数为6次。

3.3 圆端形双空心截面混凝土构件双向受力计算分析

算例取自参考文献[5]，具体计算参数见表1，并在截面上设置了一道宽0.8 m的隔板。计算结果对比见表5。可见，本文计算方法得到的结果与参考文献结果吻合较好。本次计算迭代次数为4次。

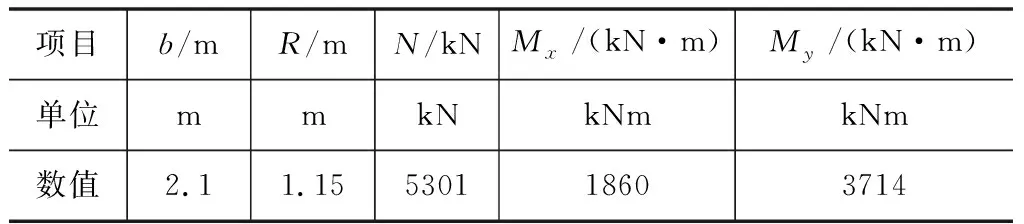
表3 圆端型实体墩截面参数

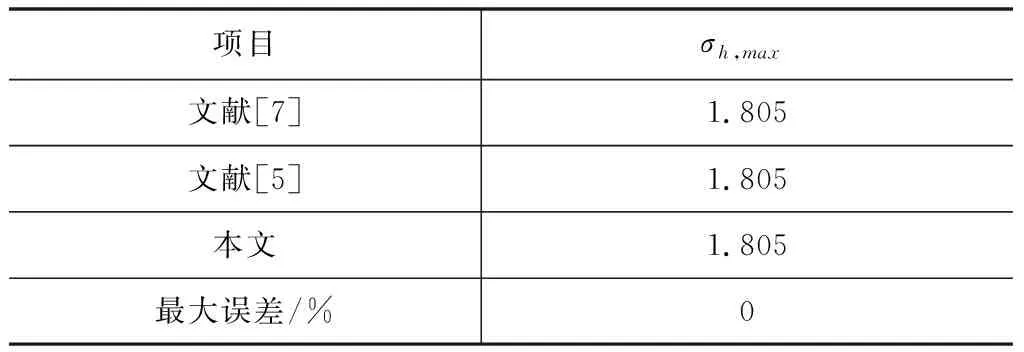
表4 计算结果对比 MPa

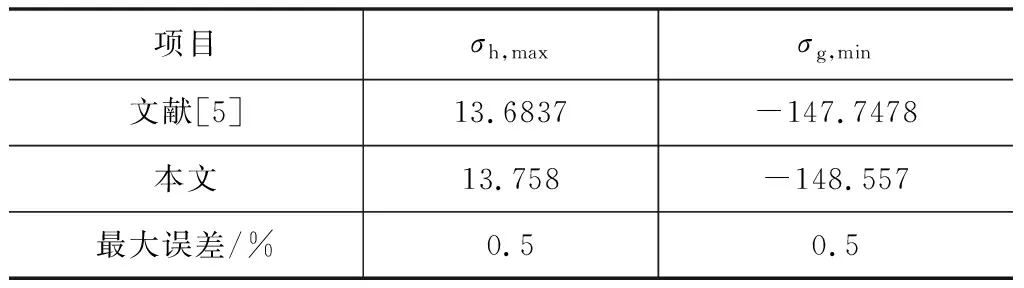
表5 计算结果对比 MPa

4 结论

(1)本文针对任意截面钢筋混凝土构件容许应力法配筋问题，以格林公式为基础，将截面轮廓转换为多段线或圆弧，导出了任意截面特性数值计算公式。

(2)对截面零应力线即开裂后截面受压、受拉区分界线迭代计算进行了简化，将对斜率k和与x轴交点b两个参数的二元非线性方程简化为对b值的一元非线性方程，采用不动点迭代法进行计算，大大提高了求解效率。

(3)运用本文方法编写的任意截面钢筋混凝土构件容许应力法配筋程序，在进行钢筋混凝土截面配筋计算和混凝土截面应力重分布计算时稳定、可靠、快捷。