桩基与膨胀土浸水室内模型试验研究

罗文豪，王金淑，饶 鸿

(西南交通大学地球科学与环境工程学院，四川成都 611756)

膨胀土是一种具有裂隙性、胀缩性和超固结性的高塑性黏土，在天然状态下较稳定，但对含水率的变化特别敏感[1]。在膨胀土的地域搭建桥梁、开挖边坡与隧道时，膨胀土的亲水膨胀性会导致与地基发生抬升、移动从而造成生命财产的损失[2]。桩基础是处理膨胀土问题的最有效的方法之一，然而开展大型原位试验是复杂、困难的。而目前有学者[3-6]基于相似理论开展室内模型试验，模拟桩基与膨胀土浸水作用并取得了不错的成效。为此本文通过自制膨胀土和桩基开展室内模型试验，为工程设计提供参考意义。

1 模型试验设计与参数

1.1 模型箱设计参数

模型箱的尺寸长×宽×高为1 m×0.3 m×1 m，壁厚20 mm，材质为透明有机玻璃。模型侧面粘贴有刻度尺，用于分析各层土的膨胀变形。在模型右侧面底部有一直径为20 mm透明排水管，其目的是防止加入水量过多，连通器原理使模型箱的水位应与导管中的水位一致，通过明确导管中水位的高度可以实时了解模型箱中水位线的位置。

此外，在模型箱的侧面有安装3排宽度约50 mm的角钢条，目的一是防止膨胀力过大造成模型箱崩坏，二是顶部的钢条便于放置传感器显示器和固定百分表。

1.2 膨胀土参数

膨胀土的质量配比为蒙脱石∶砂∶高岭土=7∶6∶1，初始含水率配置为13 %。通过试验测得了配置土体的物理性质指标，其相关的参数如表1所示。

表1 膨胀土的物理性质参数

土体的自由膨胀率为84 %，属于中等膨胀性质的土，现将配置好的土体分层夯实填入模型箱中。为使浇灌的水更容易下渗，各层膨胀土之间以20 mm厚透水性能好的砂土间隔，并在土层顶部布置有砂井贯穿整个膨胀土层，模型箱底部以砂土垫底。土层厚度及参数如模型正面示例图1所示。

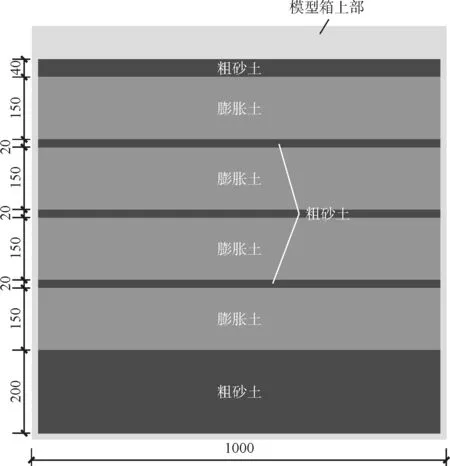
图1 模型箱中土层高度示例(单位:mm)

1.3 桩基设计与桩土作用力监测系统

以外径为31 mm、内径28 mm的PVC管模拟等直径桩基，桩基由4根单桩组成，编号分别为1#～4#，桩入土深度分别为2.5 cm、10.2 cm、19.2 cm。40.7 cm，桩间距为200 mm。各桩的入土深度及相应的埋藏位置见图2。

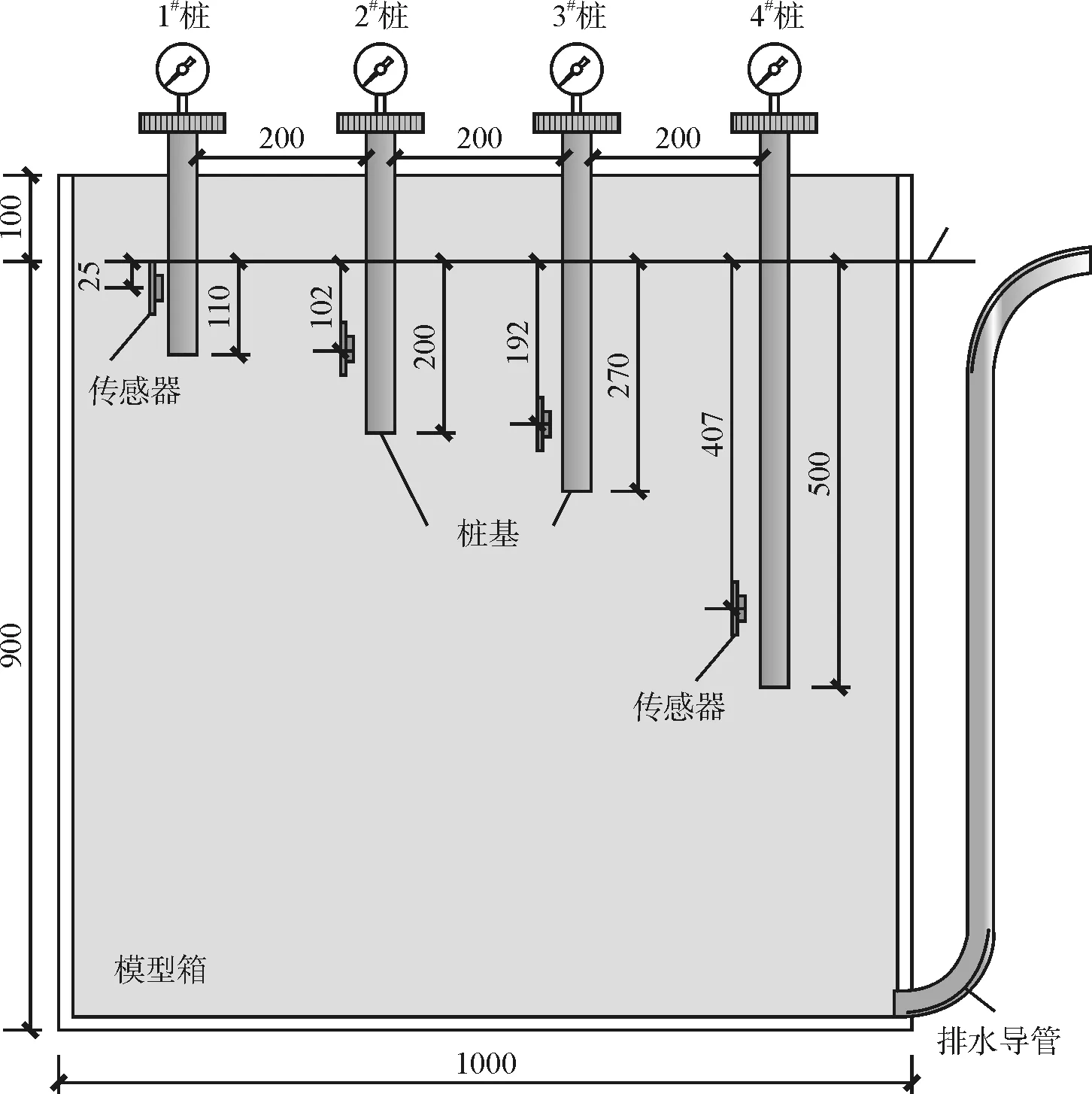
图2 桩基与传感器布置示例(单位:mm)

PVC管表面光滑，为增大桩侧表面的摩擦系数，用环氧树脂胶水涂抹在管侧壁，粘贴一层薄的石英砂颗粒。实际工程中桩基都是承受荷载的，为此在桩顶安放砝码模拟桩基承受的竖向荷载作用，其荷载大小为16.55 kPa。各桩顶上均安装有百分表监测桩顶在浸水膨胀变形过程中的位移抬升量。除此之外，在土体表层处亦布置有百分表监测土层的自由膨胀变形，并在桩周不同深度处有安装4个传感器监测土中水平应力。桩基布置及传感器安装的位置与深度见图2所示。

1.4 灌水方案

试验以人工灌水的形式加水，加水速率约为1 100 mL/h，每日加水时间约为8～16 h。试验持续加水5 d，一共灌水60.6 L，此时水面高过土层表面表明土层已饱和，故停止加水。

2 试验结果

2.1 桩身抬升规律

图3～图6分别反映了1#～4#桩身抬升量随时间变化的规律，图7将1#～4#桩的抬升量与土表层隆起量进行了对比。

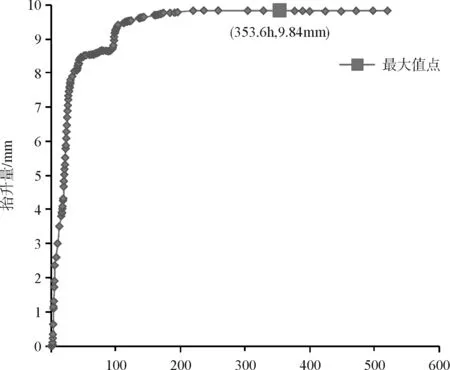
图3 1#桩抬升量与时间的关系

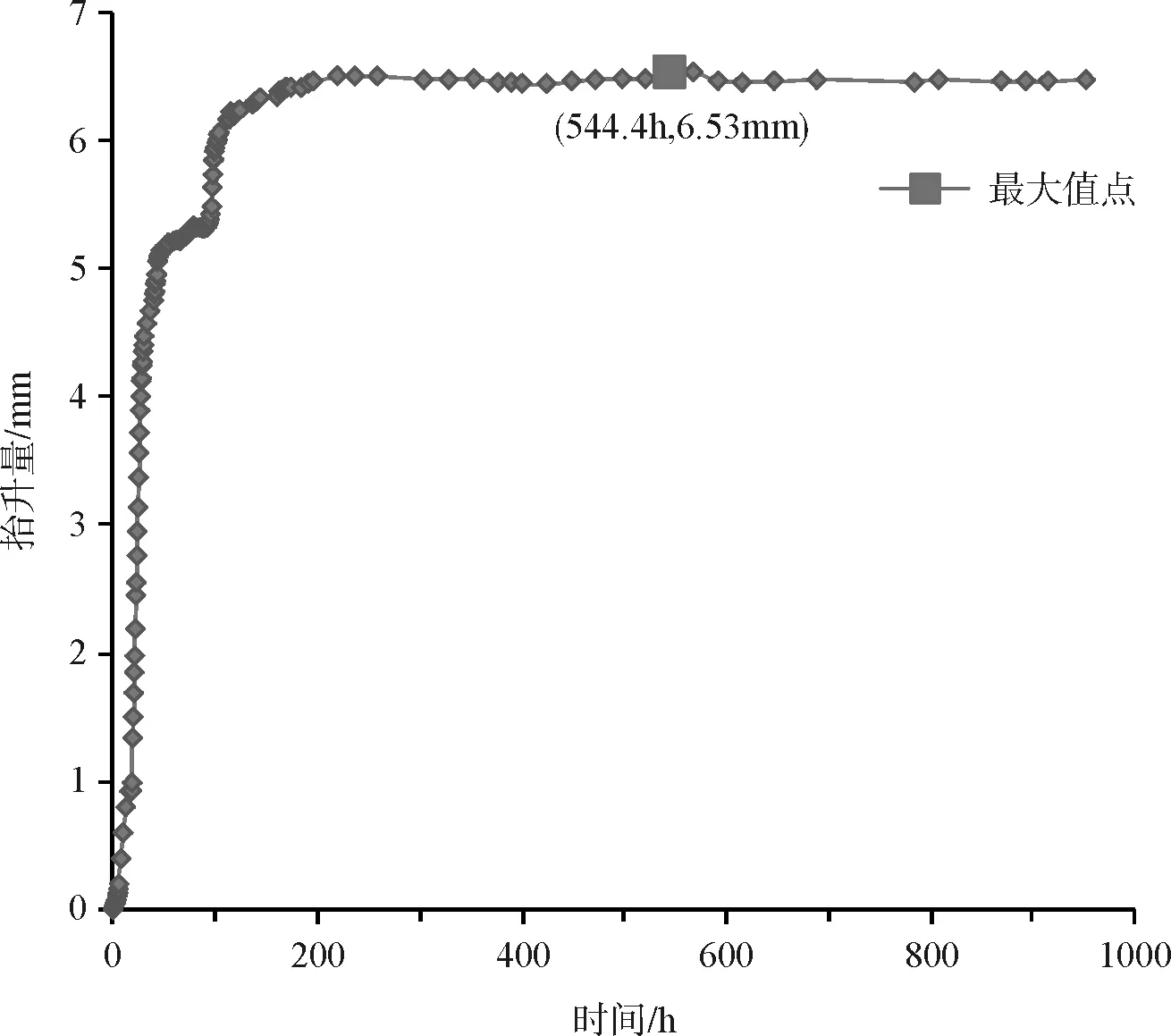
图4 2#桩抬升与时间的关系

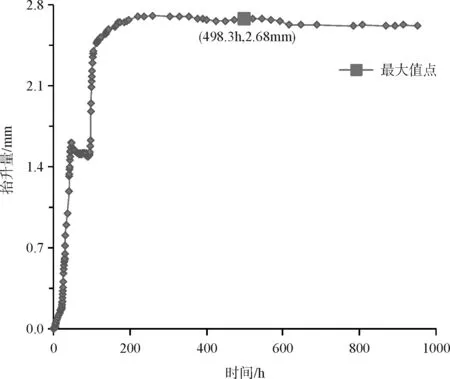
图5 3#桩抬升量与时间的关系

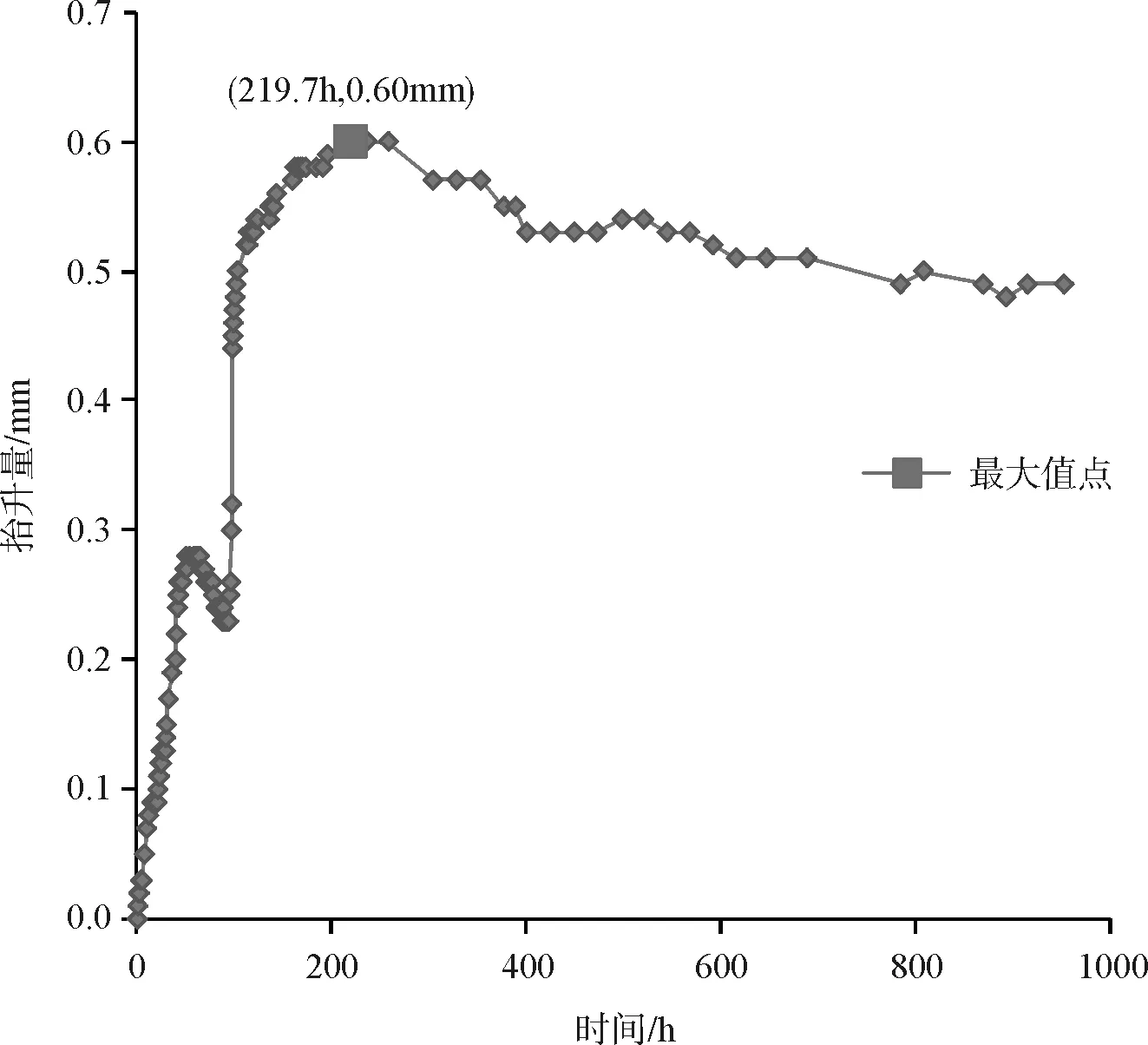
图6 4#桩抬升量与时间的关系

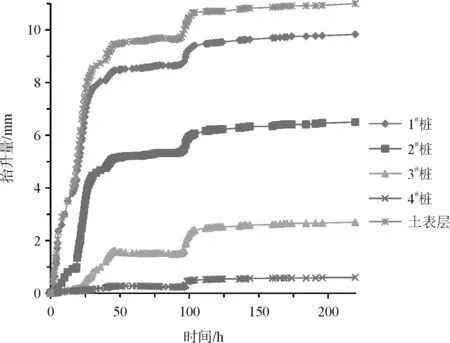
图7 1#～4#桩抬升量及土层表隆起量与时间的关系

从图7中可以看出各桩身抬升变化在整体上具有相似的增加规律，在同一时段内均具有急剧上升趋势和平缓上升趋势。各桩身位移主要变化在前140 h内，在这段时间内桩身位移大致经历先后两个急剧抬升阶段，140 h之后各桩身均平缓上升，1#～4#桩分别在353.6 h、544.4 h、498.3 h、219.7 h时间点达到抬升位移最大值。

在随后的时间段内，通过图3～图6可以看出各桩身抬升位移有不同程度的下降，3#、4#桩下降最明显，而1#、2#桩下降不明显，这是由于3#、4#桩较长，底部膨胀土层薄而无法提供相应的桩端承载力，桩基在自重和上部荷载下挤压饱和松散的土体使桩底的土体固结，反映出土体逐渐达到饱和后不再吸水膨胀。

通过记录数据得到1#桩抬升最大，4#桩最小，1#～4#桩身的抬升位移最大值分别为9.84 mm、6.53 mm、2.68 mm、0.60 mm，所占其桩长的比值分别约为87.73 ‰、31.0 ‰、9.63 ‰、1.10 ‰，桩长与抬升量呈负相关。由于各根桩顶荷载相同，均为16.55 kPa，因此将各桩身的最大抬升量与桩长进行拟合，得到它们之间的函数关系呈对数形式(图8)。

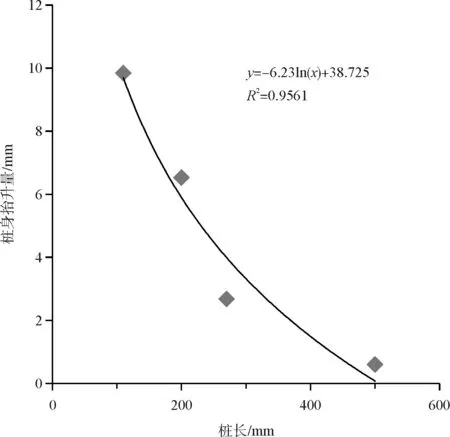
图8 竖向荷载下桩长与桩身的关系

2.2 桩身轴力变化规律分析

土体中不同深度处埋设4个监测土中水平应力的传感器，其埋设位置见图2，埋设深度分别为25 mm、102 mm、192 mm、407 mm。不同时刻土体中的水平应力如图9所示，随着加水过程的进行，土中峰值水平应力不断增大，峰值的位置不断向土层深部移动。

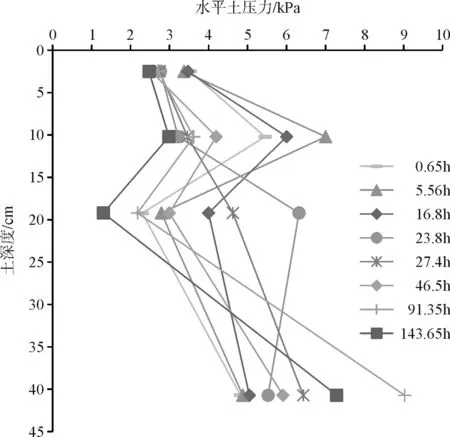
图9 土体中的水平应力沿深度变化关系曲线

为分析桩身轴力随时间的变化，我们不妨假设模型箱中土体是均一、各向同性的，因此土体中的水平应力可以认为是作用在桩周上的。以4#桩为例，通过计算得到了4#桩的桩身轴力沿桩身的分布曲线(图10)。

图10 4#桩轴力沿桩身分布

由图10不难看出，由于桩顶存在荷载故在桩尖上部轴力为受压的负值，其它部位受浸水膨胀作用桩身表现出拉应力。从形态上看，各个时间段轴应力沿桩身均出现先增大后减小的趋势，并且随着时间增加，桩身轴应力在各个深度有不断增大的趋势，达到最大值后所有减小。轴应力在桩身中下部达到应力峰值点，桩身轴力的峰值即为胀切力，通过计算胀切力最大值约为229 N；轴力峰值点的位置即为中性点的位置，中性点以上桩身轴力沿桩身增大，中性点以下轴力沿桩身减小，在桩底减小到0。

2.3 膨胀变形沿土层深度变化规律

如前文图1所示，模型从上至下共有4层膨胀土，每层层厚均为150 mm，各膨胀土层之间由薄砂土层隔开，因此各层膨胀土与砂土层有清晰明显的分界线，模型箱各侧面已有刻度尺标记模型箱的标高。由于砂土不会随着浸湿过程产生膨胀变形，因此各层膨胀土的沉降变化可以通过记录土层分界线的高度变化反映出来。

为避免人工读数造成的误差，模型箱侧面共设计有6组刻度尺，通过计算得到各组刻度尺上标记的土层厚度，取它们的平均值作为各膨胀土层的厚度进行分析。

图11反映了从上至下各层膨胀土层在不同时间点相比初始时刻的厚度变化量。可以看出在加水后第1、2层土最先膨胀，而第3、4层土由于水下渗需要时间，在约19.4 h时才开始膨胀，最终第1、4层的膨胀量比第2、3层要大一些。

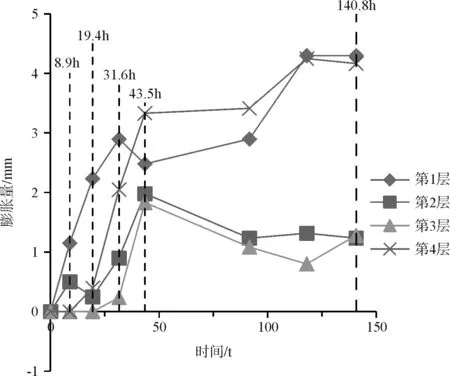
图11 各层膨胀土厚度随时间变化的关系

图12给出了8.9 h时刻土体的膨胀量随土层深度变化的规律，结合图11可以看出，在8.9 h时上部1、2层大致呈线性膨胀，膨胀深度约从0～250 mm，而下部3、4层由于只有少量的水渗至该高度，故基本未出现膨胀。

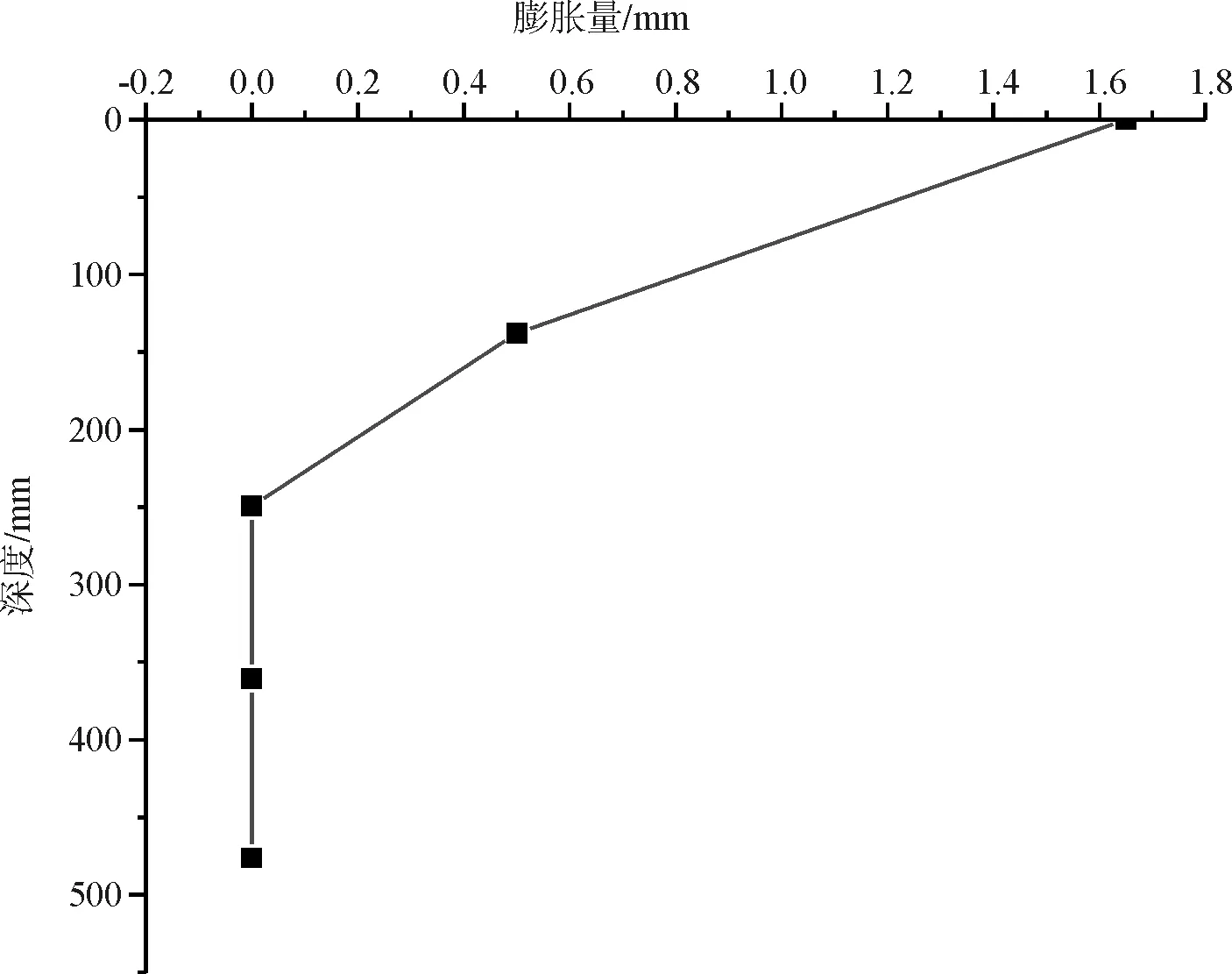
图12 8.9h时膨胀量与土层深度关系

图13给出了19.4 h时土体的膨胀量随土层深度变化的规律，此时膨胀量与深度之间呈现非线性关系。结合图11不难看出该时段第1层膨胀加快，而下部2～4层土自身膨胀较缓慢，说明仍仅有少量水渗透到下方的土层中，而加入的水具有自重作用在下部的土层中，使得2～4层土在第1层土体膨胀挤压以及加入的水的重力作用下其膨胀量出现了负值。但由于第1层膨胀过快，土层整体上还是呈现膨胀的现象，并且膨胀量不断增大。

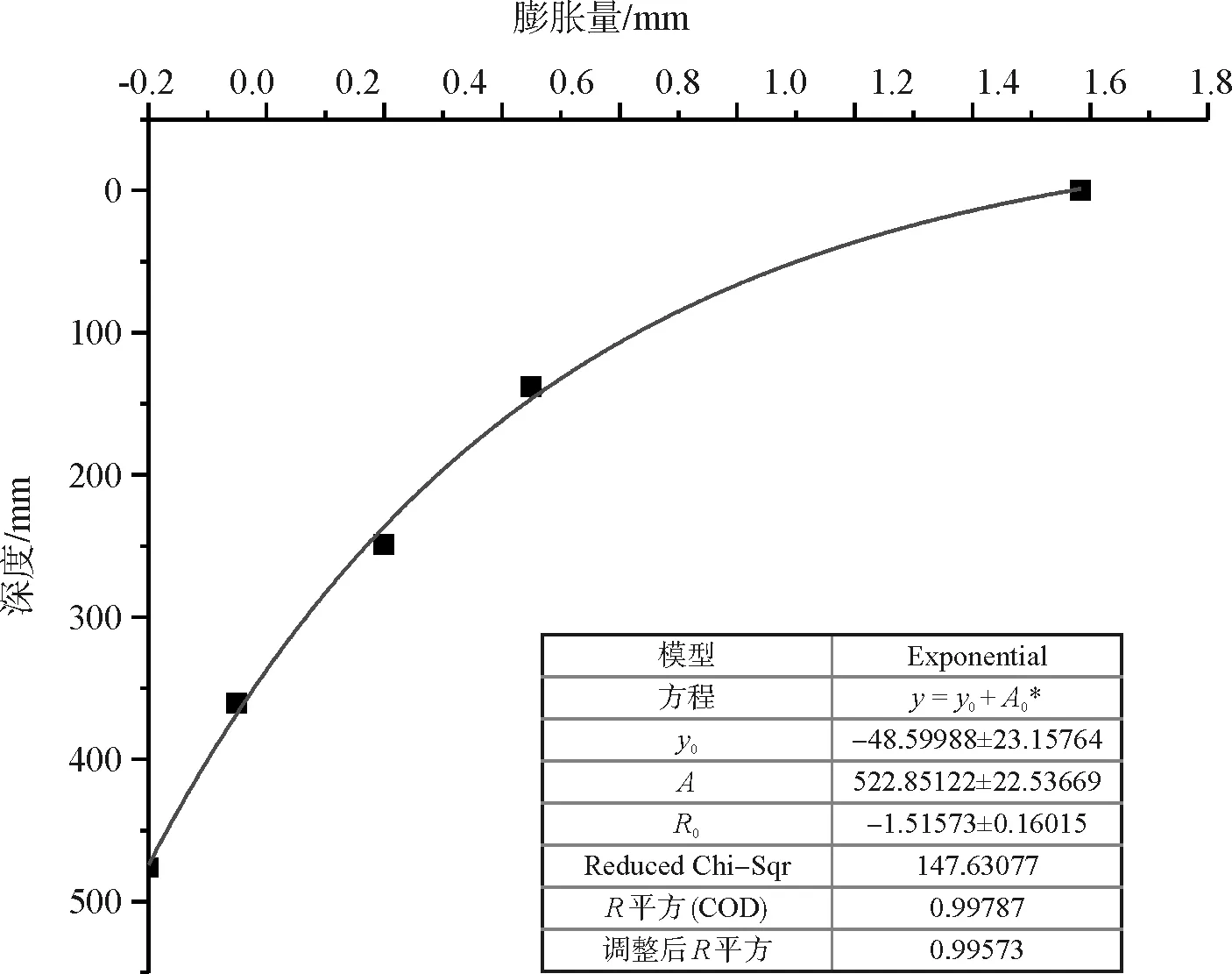
图13 19.4h时膨胀量与土层深度关系

图14、图15给出了43.5 h、140.8 h时土体的膨胀量随土层深度变化的规律。发现浸水初期，土层上部大致呈线性隆起，下部无膨胀。随着下部土层逐渐吸水膨胀，它们之间的关系从非线性关系转变为线性函数，因此土层整体的膨胀速率随时间是减少的，这与前文测得土表层的数据相符。

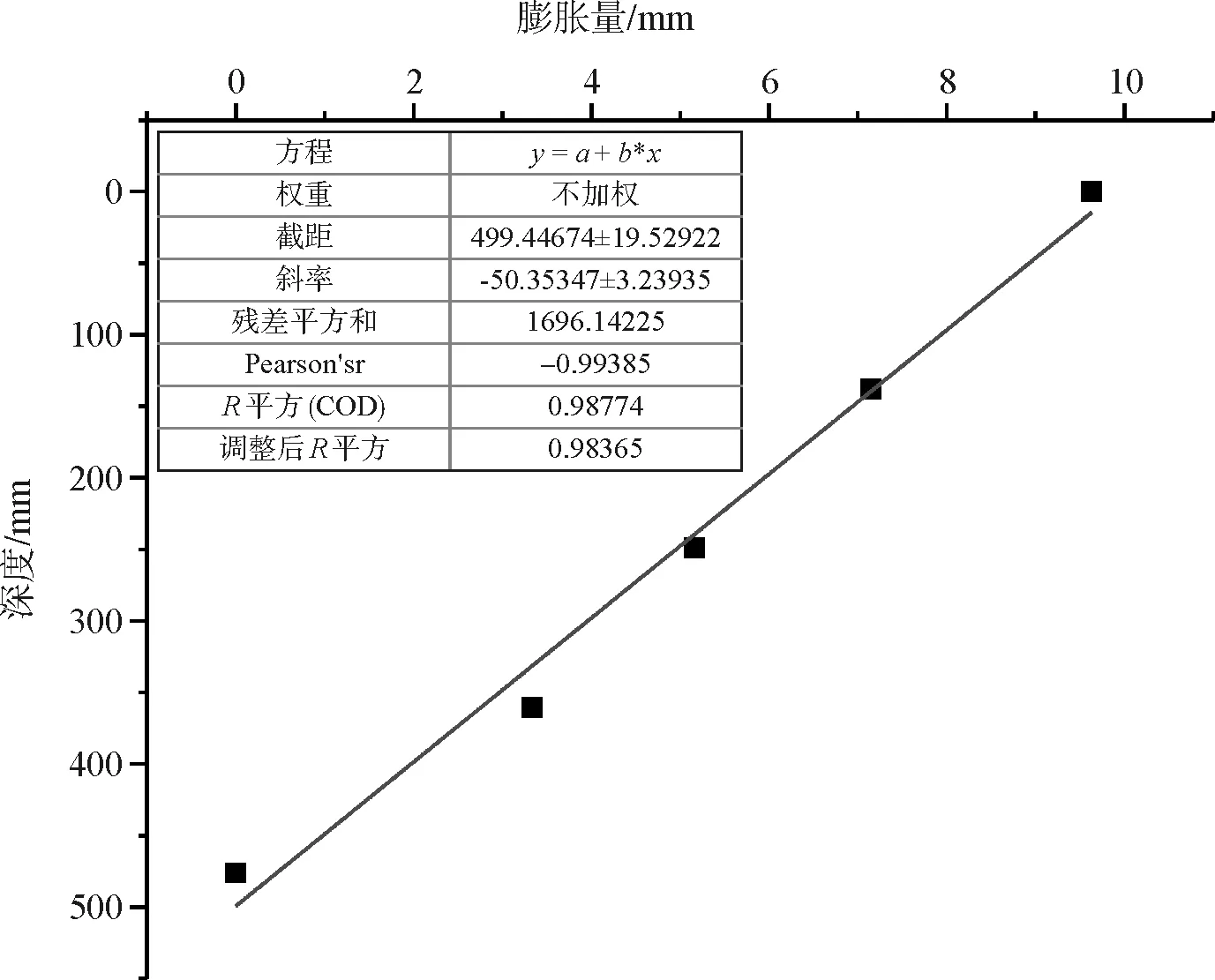
图14 43.5h时膨胀量与土层深度关系

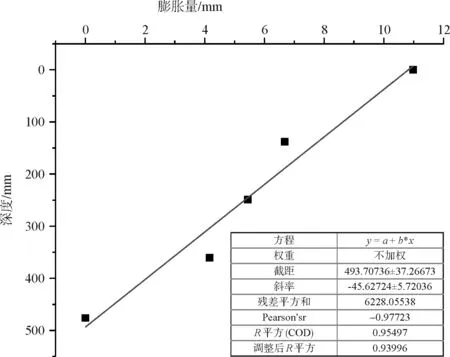
图15 140.8h时膨胀量与土层深度关系

图16反映了第1～4层土的膨胀量叠加得到的净膨胀量值与土表层测得的膨胀量的对比，可以看出两组数据大体相符，说明了通过此方法计算各层膨胀土膨胀变量的正确性。

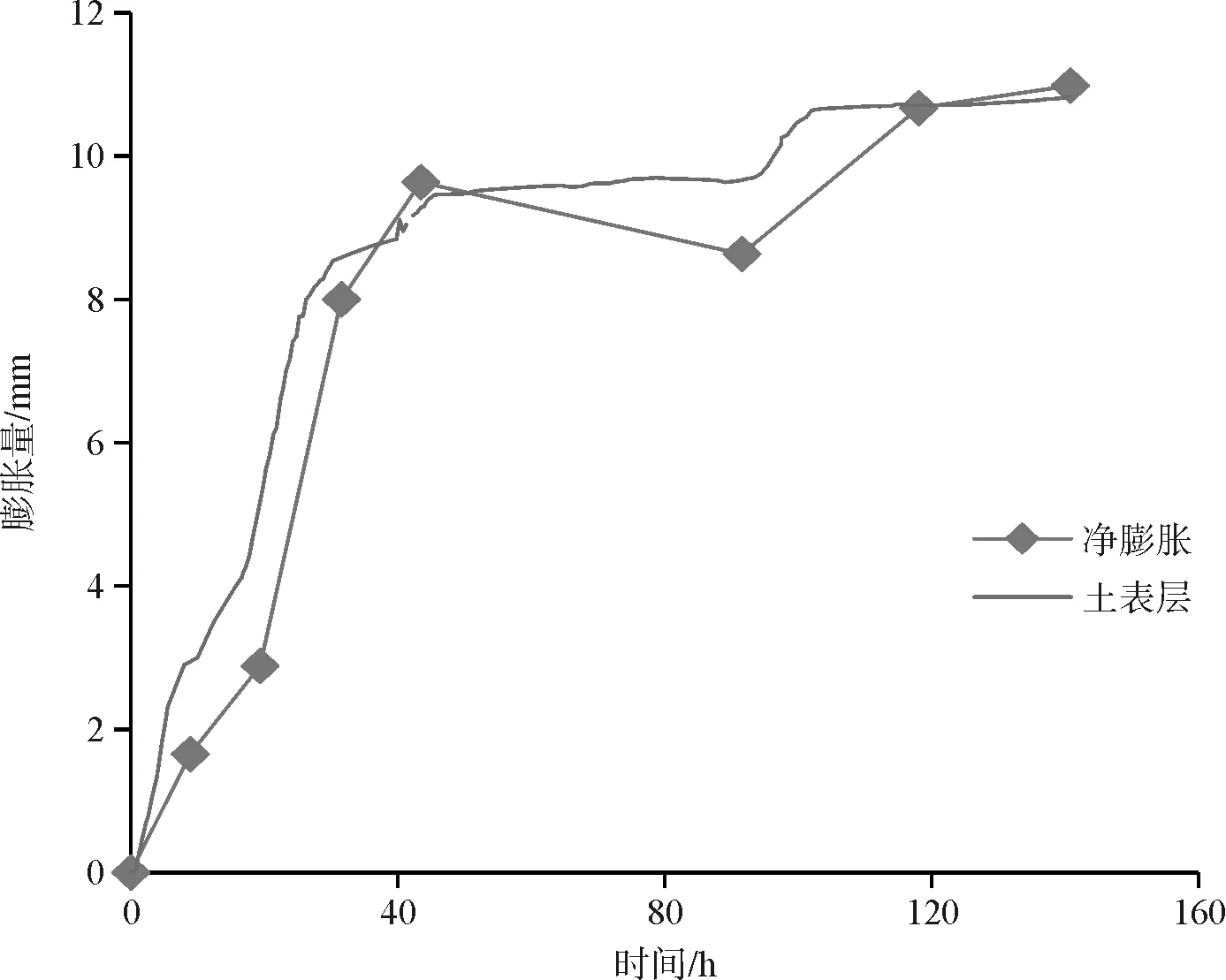
图16 净膨胀量与土层表膨胀随时间变化值

3 结论

本文按照蒙脱石∶砂土∶高岭土的质量比例为7∶6∶1配置膨胀土，初始含水率以最优含水率的值13 %设置。使用不同长度的PVC管模拟桩基，在桩顶施加竖向恒定荷载，模拟桩基与膨胀土浸水作用的室内模型试验，得到了如下的结论：

(1)分析了各桩身抬升量随时间变化的规律，随桩入土深度增加，桩身抬升量是以对数函数的形式减少，其关系式为y=-6.23ln(x)+38.725。

(2)假设模型箱中土体是均一、各向同性的条件下，得到了土中的水平应力随土层深度的分布变化的规律，并通过计算得到了4#桩的轴力沿桩身变化的分布规律。

(3)浸水初期，水无法下渗至深度土层，导致只有土层上部呈线性膨胀，下部没有膨胀。随着水流逐渐下渗，土层膨胀量与深度的关系逐步呈现为线性函数，并且土层深度与膨胀量呈负相关。