考虑综合运输成本的多式联运路径优化问题
李魁梅,郑 波
(1.重庆邮电大学移通学院 淬炼商学院,重庆 401520;2.重庆广播电视大学 管理学院,重庆 401520)
随着“一带一路”国家战略和“长江经济带建设”的推进,经济和贸易全球化进程加快,对运输的要求也愈来愈高,多式联运在现代物流运输中的地位越来越重要,成为当前研究的重点和热点,取得了丰富的研究成果。分析相关文献可知,相关研究主要集中在影响多式联运路径优化的因素和路径优化算法研究两方面。影响因素方面,随着环保意识的增强,将尾气排放、噪音污染等造成的运输负外部性损失进行核算。Ricci等[1]将污染造成的外部成本考虑到运输成本中,构建了货物运输的社会成本计算模型,有重要参考价值。Macharis[2]提出运输价格有效定价的途径是外部成本内部化,并在外部成本内化这一前提下,研究了燃油价格波动对多式联运服务范围的影响。而国内一般仅将二氧化碳排放作为外部性的考虑因素,如文献[3]在进行多式联运综合满意度建模时,将政府满意度直接与二氧化碳排放量挂钩。在模型方面,学者们分别提出了基于成本最小、运输时间最少和运输距离最短的多式联运数学模型[4-6]。在算法方面,现有研究主要聚焦于智能算法,如文献[7]用字符对个体进行编码,提出了一种求解带时间窗多式联运问题的和声算法。文献[8]提出了遗传算法和蚁群算法相结合的混合算法。文献[9]则提出了基于固定优先权编码的遗传算法,求得了长大货物多式联运问题的最优解。
根据文献研究发现,在进行多式联运路径优化研究时,影响因素方面仅仅将时间因素作为约束条件,并没有转化入目标函数中,更没有考虑尾气排放外部成本(或者单纯考虑二氧化碳排放)。此外,因为市场竞争激烈,越来越多的产品对时间敏感,比如笔记本电脑、时装等,所以在进行路径优化时有必要增加考虑产品的价值特性,即衰变成本。基于此,本文提出将运输过程中的排放、在途库存、不准时(提前或逾期)和衰变构建成本模型,结合运输工具成本,获得综合运输成本模型,进而以综合运输成本最低为目标构建多式联运路径优化模型。针对模型求解,因与一般智能算法相比,BA算法全局寻优能力较强、稳定性较好,不足之处在于收敛速度较慢,所以本文引入混沌机制、动态自适应惯性权重、非均匀变异策略和反馈机制,获得改进的HBA算法求解模型。
1 问题描述及数学模型
1.1 问题描述及假设
一批货要从起点城市运输到终点城市,且两者之间有若干城市可以中转,且任意相连的两个城市可能有多种运输方式供选择,除起点和终点外,每个节点均可实现货物在不同运输方式之间进行转换。根据文献[3]和[8],结合各运输方式市场供给情况,遵循合理假设原则,在如下假设条件(约束条件)下,合理规划运输方案,使综合运输成本最低。
1) 运输和中转工具运载能力充足,满足货物运输和中转需求;
2) 只考虑运输的成本和时间,不考虑中转的成本和时间;
3) 城市之间可以根据运输条件自由选择多种运输方式,但每种运输方式均不能超过该方式最大载重约束。
1.2 综合运输成本模型
综合运输成本由运输会产生排放成本、在途成本、不准时成本、衰变成本和工具成本构成。
1.2.1 排放成本
运输中产生的排放物主要包括CO2、CO、NOX、PM、SO2、HC等6种,且不同运输方式下各排放物的单位排放量和不同排放物的单位排放成本不一样[10]。第k种运输方式下,运输单位货物单位距离的排放成本如式(1)所示。

式中,k∈{1,2,···,K},且K=3,分别表示公路、铁路和水路运输; Ω∈{1,2,· ··,6},分别表示CO2、CO、NOX、PM、SO2、HC 6 种排放物;EkΩ表示第k种运输方式第 Ω种排放物单位排放量;CeΩ表示第Ω 种排放物单位排放成本。
1.2.2 在途成本
货物运输过程中会占用大量资金,且产生保险、仓储、税费、搬运等费用,进而造成在途成本。根据文献[11],单位货物单位时间产生的在途成本为

式中,GV表示货物价值;H表示货物单位时间持有成本。
1.2.3 不准时成本
不准时(提前或逾期)成本指未按照客户规定时间送达货物而产生的惩罚性费用为
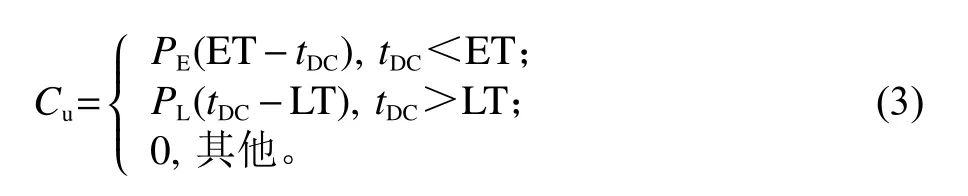
式中,[ET, LT ]为客户规定货物送达的时间窗;tDC为货物送达目的城市DC的时间;PE、PL分别为货物早送达和晚送达的单位时间惩罚成本。
1.2.4 衰变成本
货物价值通常会随着时间衰减,进而产生衰变成本。文献[11]用λ表示单位时间衰变率,则单位货物单位时间衰变成本为

1.2.5 工具成本
工具成本指运输过程中产生的运输工具租赁费用、油耗费用和司机薪酬等。如果已知利用第k种运输方式运输单位货物单位距离的工具成本为则再乘以运输距离和货物重量即可求得工具成本。
1.3 模型建立
I为运输货物总量;V为城市集合;m为城市节点数;dijk为城市i和j之间第k种运输方式的运输距离;tijk为城市i和j之间第k种运输方式的运输时间;分别为城市i和j之间第k种运输方式的最大载重和实际载重;eijk为0-1变量,表示是否采用第k种运输方式。
建立基于综合运输成本最小的多式联运数学模型。
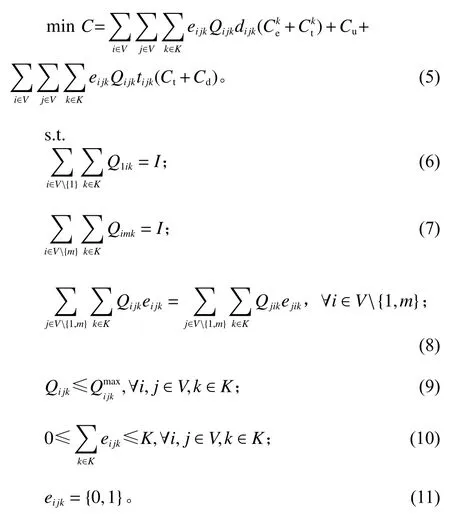
式(5)表示运输成本最小的目标函数;式(6)表示起点城市运输货物量为输入流量;式(7)表示所有货物送达终点城市;式(8)表示每个城市的输入流量与输出流量相等;式(9)表示两个城市之间任一运输方式运输量均不能超过该方式最大载重约束;式(10)表示城市间可选择多种运输方式;式(11)表示0-1变量约束。
2 基于混合蝙蝠算法的模型求解
2.1 标准蝙蝠算法
蝙蝠算法(BA)是一种基于迭代的优化技术,初始化为一组随机解,然后通过迭代搜寻最优解,且在最优解周围通过随机飞行产生局部新解,加强了局部搜索,是一种搜索全局最优解的有效方法。与其他算法相比,蝙蝠算法(BA)在准确性和有效性方面远优于其他算法。蝙蝠算法(BA)包括搜索和寻优两大机制[12-13]。
2.1.1 搜索机制
搜索机制主要利用频率h对蝙蝠位置和速度进行更新。在D维空间中,用和(xb1,xb2,···,xbD)分别表示蝙蝠b在t时刻的速度和位置,则t+1时刻更新为
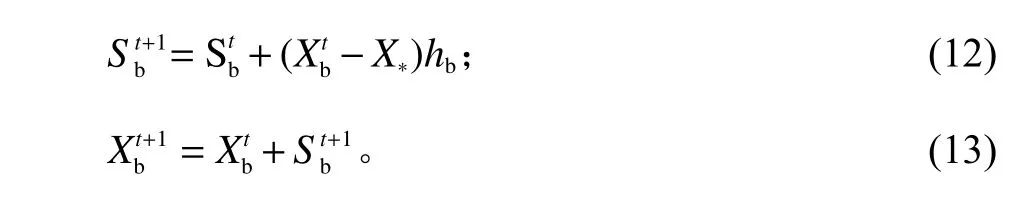
式中,X∗表示当前最优蝙蝠所在位置;hb=(hmax−hmin)φ(φ为服从均匀分布的随机数,取值范围为[0,1])。
2.1.2 寻优机制
通过寻优机制,每只蝙蝠位置Xold在最优个体附近搜索,并根据式(14)更新位置。

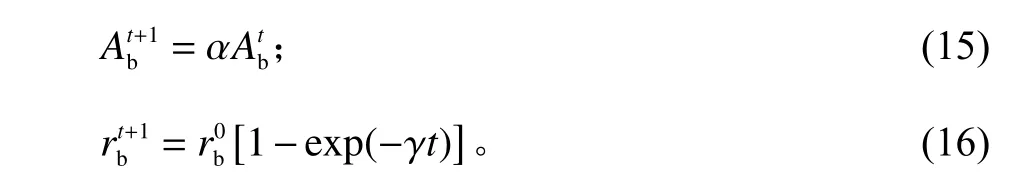
2.2 编码及解码方式
2.2.1 全局流量按比例分配

式中,σi表示第i条路径的货物流量比例;xi表示第i条路径的货物流量;C1s表示与第i条路径同一等级的所有路径集合(输出节点为s)。则第i条路径承担的货物流量为

式中,Oflows表示路径i对应输出节点s的输出流量值。如图1所示,路径4对应流量输出节点1,且同一等级路径集为C11={1,3,4,5,6}。 因此,σ4=x4/用Oflow1表示节点1输出流量,则路径4的流量全局流量的按比例分配的具体流程如图2所示。
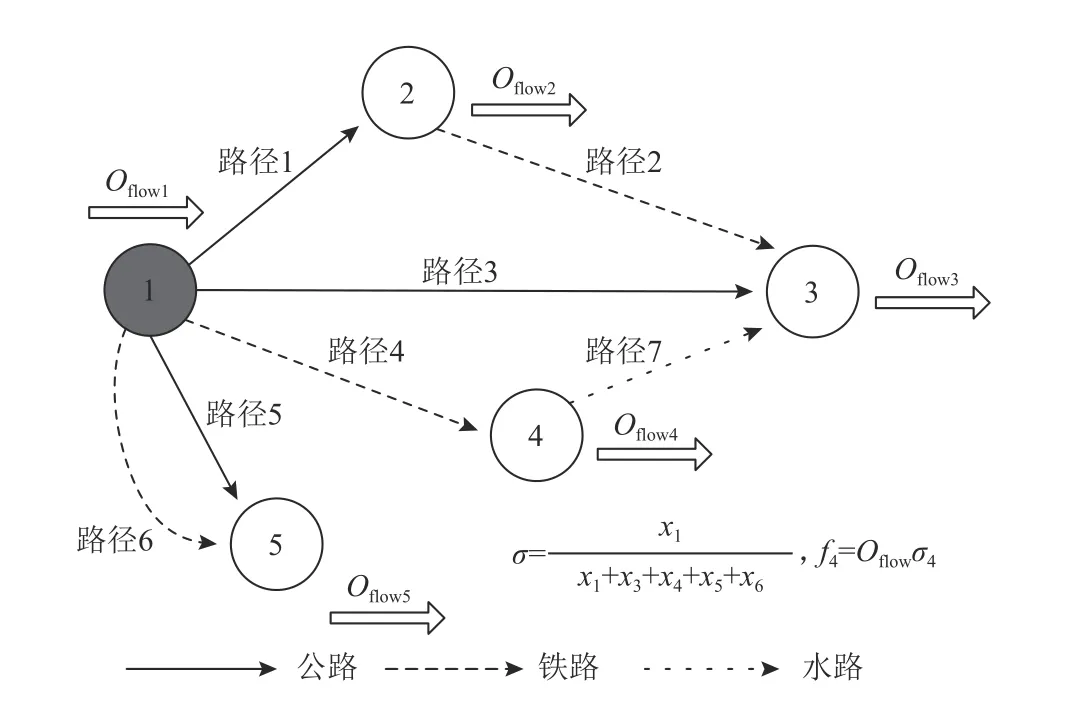
图1 全局流量按比例分配Figure 1 Proportional distribution of global flow
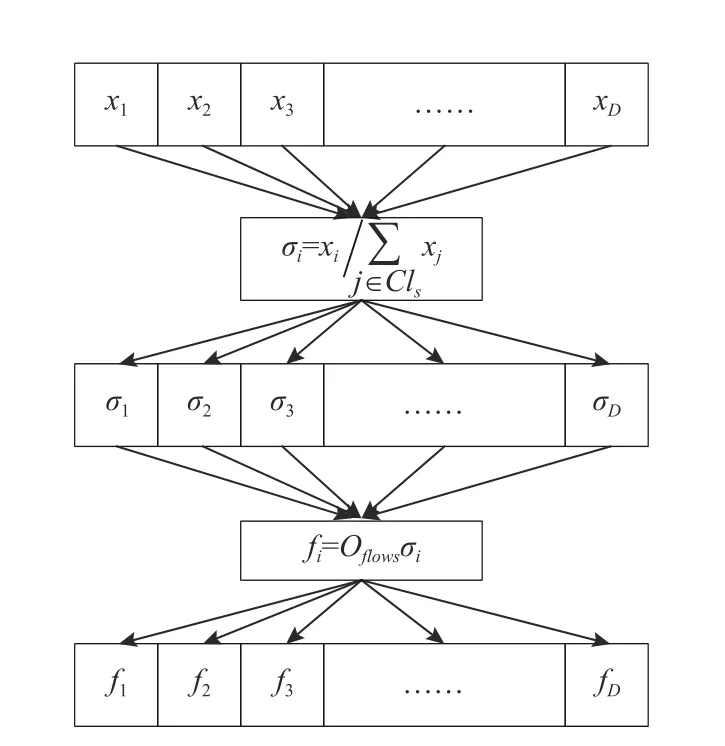
图2 全局流量分配流程Figure 2 Distribution process of global flow
2.2.2 局部流量返上级分配
实际上,每条路径的货物承载能力有限,简单按比例进行流量分配,必然产生较多不可行方案,进而影响算法求解效果。对此,本文设计了将节点超额流量返回上级节点进行再次分配的思路。具体操作流程为:判断节点输入流量和最大流量约束大小,如果输入流量大于最大流量约束,则需要进行局部调整计算节点超额流量,即输入流量和最大流量约束之差;将超额流量返回上一节点,按满载率对其他可行路径进行排序,依次分配超额流量,优先满足单条路径满载。根据前文可知,节点4 输入流量为f4,其对应输出路径为7。用flimit,i表示路径i的最大流量约束,那么如果f4>flimit,7,则节点4流量超额,需要进行局部调整。如图3所示,用fleft4表示节点4的超额流量,取值为f4−flimit,7。将fleft4返回节点1进行再次分配,可知节点1对应的输出路径还有1、3、5和6。计算每条路径满载度 De=flimit−f,并进行降序排序,然后将fleft4进行依次分配。用qi(i∈{1,3,5,6})表 示各条路径再次分配流量,则0≤qi≤Dei,如图4所示。通过上述过程,便能实现超额流量的再次分配,大量减少不可行方案的产生。
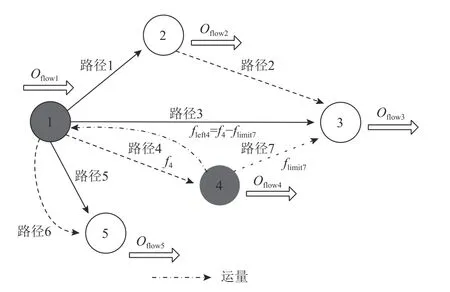
图3 超额流量返回上级节点Figure 3 Excess flow returned to parent node
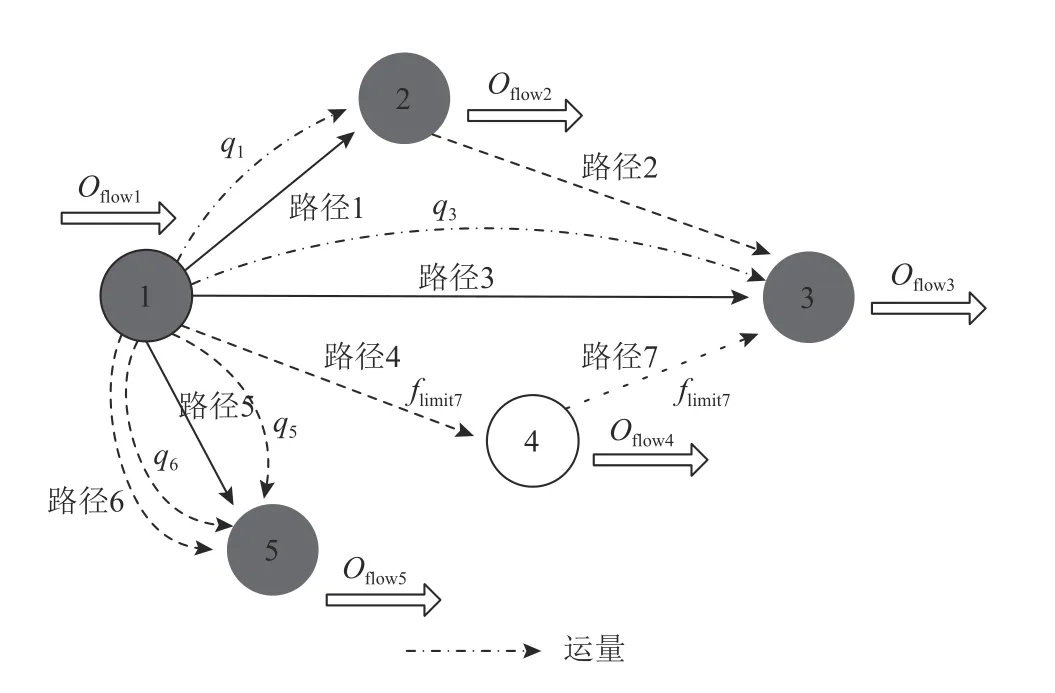
图4 上级节点超额流量再分配Figure 4 Reallocation of excess flow in superior nodes
2.3 设计适应度函数
适应度值是评判个体优劣的重要标准,本文根据式(5)设计算法适应度函数为
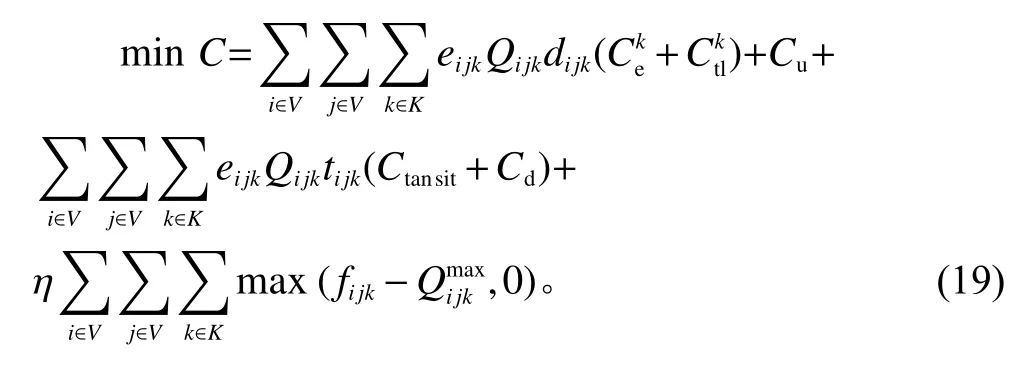
式中,η为正值常数。
2.4 引入混沌状态
智能算法初始种群质量决定着算法的收敛速度和求解精度[6]。标准BA算法在缺乏有关先验信息的情况下,采用随机方式生成初始种群,无法确保初始种群在解空间中的均匀分布。对此,本文利用混沌系统的随机性、遍历性和规律性来优化蝙蝠初始位置,提高初始种群质量,增强算法求解性能。具体包括两个步骤:首先,根据式(20)构造大量蝙蝠位置和速度向量;然后择优选择部分个体组成蝙蝠初始种群。
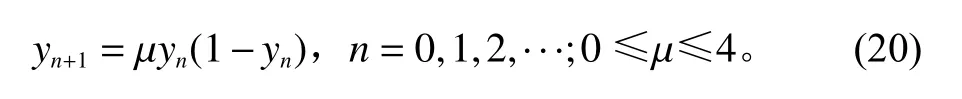
式(20)为Logistics映射(迭代),µ为控制参数。当 µ=4时 ,y0∈(0,1),表示Logistics处于完全混沌状态。
2.5 引入动态自适应惯性权重
根据式(12)可知,标准BA 算法速度更新系数恒定为1,不但大大降低了种群多样性和个体灵活性,还导致算法在寻优过程中不能很好地平衡局部搜索和全局搜索的关系,进而影响算法寻优效率。针对该问题,本文提出一种动态自适应惯性权重系数,具体表达式如式(21)所示。
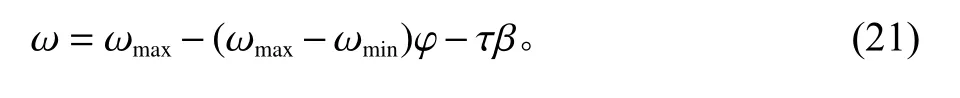
式中,ωmax、 ωmin分别为 ω的最大值和最小值;φ表示服从均匀分布的随机数,取值范围为[0,1];τ表示惯性偏离因子,取值范围为[0.1,0.9]; β表示服从贝塔分布的随机数,取值为范围为(0,1)。分析式(21)( ωmax−ωmin)φ使 ω能 够 在[ωmin, ωmax]内 随 机 取值,而贝塔分布随机数 β让ω 随 机偏离,使得 ω的取值分布更加均匀和灵活。同时,在 β前加入τ,很好地控制了 ω的偏离幅度。可以看出,引入动态自适应权重,不但可以增加代与代之间的蝙蝠随机性,也增加了每一代内蝙蝠的随机性,提高了蝙蝠种群多样性。
在标准BA算法中引入动态自适应惯性权重,则算法速度更新公式变为

2.6 引入非均匀变异策略
针对标准BA算法容易陷入局部最优解的问题,本文采用非均匀变异操作对其进行改进。与遗传算法变异算子不同,非均匀变异操作能够根据迭代次数自适应调整搜索步长,进而使算法在进化过程中始终保持跳出局部最优解的能力[13]。如式(23)所示,如果对蝙蝠个体Xi=(xi1,xi2,···,xin,···,xiD)进行变异操作,则第n维位置向量变异为
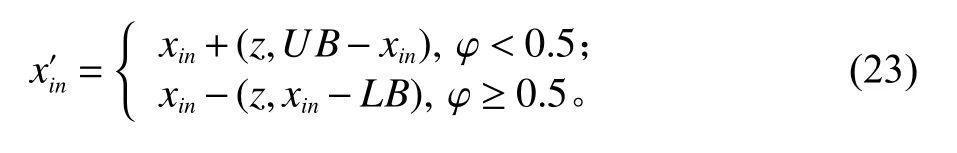
式中,UB、LB分别表示当前迭代中所有蝙蝠个体第n维变量的最大值和最小值;(z,y)=y(1−φ(1−z/Z)Λ),表示非均匀变异步长,z表示当前迭代次数,Z表示最大迭代次数;φ表示服从均匀分布的随机数,取值范围为[0,1];Λ表示非均匀度参数。分析可知,通过非均匀变异操作,算法在迭代初期拥有较大的搜索范围,提高了全局寻优能力。随着迭代次数的增加,搜索半径逐渐减小,算法只能在当前解附近进行搜索,提高了算法搜索精度。
2.7 引入反馈机制
在标准BA 算法中,蝙蝠个体通过不断更新自身位置和速度来靠近猎物,运动方式比较单一[10]。对此,本文引入信息反馈机制,即每次迭代中最优个体与最差个体进行信息反馈,通过这种信息交流,引导距离猎物较远的个体快速抵达猎物附近,进而提高算法收敛速度。信息反馈机制如式(24)所示。
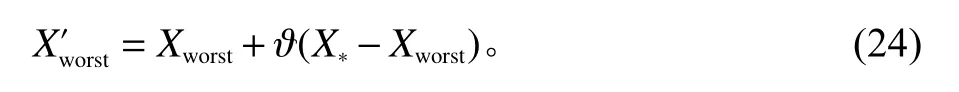
式中,Xworst、X∗分别表示当前最差和最优蝙蝠所在位置;ϑ表示服从均匀分布的随机数,取值范围为[0,1]。
2.8 模型求解步骤
根据前文所述,采用混合蝙蝠算法HBA求解多式联运问题的流程如下。
步骤1设置算法参数,包括候选种群规模M、初始种群规模N、最大迭代次数Z、最大和最小惯性权重ωmax、ωmin等。
步骤2随机生成一个实数数组 (x1,s1)并按照式(20)生成其他D-1维向量,作为蝙蝠b的位置和速度向量 (Xb,Sb)。同理,可生成其他M-1个蝙蝠个体。对于Xb,根据3.2节进行解码,并根据式(19)测算适应度值C(Xb)。择优选择N个蝙蝠个体组成初始种群。
步骤3记录当前种群最优个体X∗及目标函数值gC。
步骤4判断是否迭代了Z次。是,输出种群最优个体X∗,算法停止;反之,进入步骤5。
步骤5根据式(21)和(22)更新蝙蝠个体的速度向量,再按照式(13)更新位置向量。
步骤6生成随机数rand1,满足条件,则按照式(23)更新蝙蝠个体i得到Xnew,进入步骤7;反之,进入步骤8。
步骤7生成随机数rand2,同时满足rand1>A(b)和C(Xnew) 步骤8按照式(15)和(16)更新A(b)和r(b)。 步骤9选择种群最差个体,按照式(24)进行更新,返回步骤4。 本文采用包括公路、铁路和水路3种运输方式的随机运输网络来验证HBA算法的有效性。如图5所示,该运输网络共有10个节点,节点1为起点城市,节点10为终点城市。不同节点之间的运输方式可以分为单一运输和多式联运,如节点4到节点6只有铁路运输,节点7到节点8包括公路运输和铁路运输,可以同时选择2种方式进行运输。运输网络中,括号内数值分别表示不同运输方式的运输距离(单位为km)和最大容量限制(单位为t)。一般来说,公路运输运载能力不存在约束。 图5 公路、铁路、水路联运网络Figure 5 Intermodal transport network of Road, railway and waterway 企业需要从节点1运输重量500 t、价值880万元的货物到节点10,节点10的时间窗为[18,23],不准时惩罚成本为每小时0.45 万元,单位货物持有成本系数为每小时0.0003%,单位货物衰减率为每小时0.018%,公路、铁路、水路运输速度分别为80 km/h、100 km/h和54 km/h,运输工具成本分别为80元/( t·km)、40元/( t·km)和16元/ (t·km),不同运输方式排放量和排放成本[14]如表1所示。 表1 3种运输方式平均排放量和排放成本Table 1 Average emissions and emission costs of three transportation modes 利用HBA算法对上述算例进行50次求解,收敛情况如图6所示,最优运输方案如图7所示(图中数值表示对应运输方式运输货物的重量),最优运输成本为2.56万元。由此可见,多式联运路径优化模型可行有效且HBA算法能够适用于多式联运问题的求解。 为进一步验证HBA算法的求解性能,分别采用HSA算法[7]和HA算法[8]对上述算例进行50次求解,最优值对应收敛状况如图8所示,仿真结果如表2所示。 图6 HBA算法收敛图Figure 6 Convergence graph of HBA algorithm 图7 最优运输方案Figure 7 The optimal transportation scheme 图8 不同算法收敛对比Figure 8 Convergence comparison of different algorithms 表2 不同算法仿真结果对比Table 2 Comparison of simulation results between different algorithms 分析图8可知,与HSA算法和HA算法相比,HBA算法收敛较快,且求得运输成本最低,说明HBA算法具有较好的求解性能。 由表2可知,在全局寻优能力上,HBA算法能够求得最优值,且最优值搜索成功率高达90%,HSA算法和HA算法最优值搜索成功率均为0,故HBA算法全局寻优能力最强。在算法稳定性上,HBA算法求得最劣值、平均值依次优于HA算法和HSA算法,所以算法稳定性由强到弱排序为HBA算法、HA算法和HSA算法。在算法运行速度上,各算法平均迭代次数和计算时间从小到大依次为HBA算法、HSA算法和HA算法,可见HBA算法在提高算法全局寻优能力和稳定性的同时,保持了较快的运行速度。综上所述,HBA算法在求解多式联运问题上优于HSA 算法和HA算法。 1) 为更加客观全面反映运输生产实际,将客户满意度和企业责任相结合,构建考虑运输工具尾气排放、在途库存损失、不准时损失和衰变损失以及传统意义的运输费用5个方面的多式联运路径优化模型。 2) 模型计算采用混合蝙蝠算法(HBA)求解,算法在标准BA算法基础上,改进了算法解码方式,引入了混沌机制、动态自适应惯性权重、非均匀变异策略和反馈机制。 3) 通过算例分析表明,多式联运路径优化模型可行有效,且HBA算法在全局寻优能力、算法稳定性和运行速度上均优于HSA算法和HA算法,有效提高了蝙蝠算法求解多式联运问题的性能。3 仿真分析
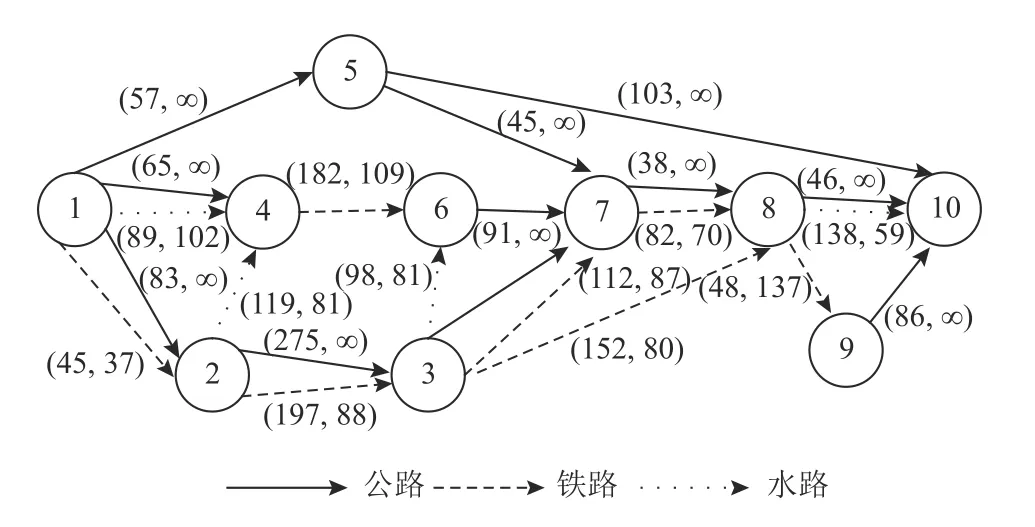

4 结论

