基于树根桩地基加固法的井塔纠偏方案
(北京科技大学金属矿山高效开采与安全教育部重点实验室,北京,100083)
随着采矿生产产量逐年增加,由于井塔的提升系统需要改造或超负荷运行,以及井塔基础发生不均匀沉降,导致井塔经常出现偏斜等现象[1]。井塔基础的不均匀沉降对矿井的正常运行造成严重影响[2],因此,针对井塔施工完成后发生的基础不均匀沉降导致井塔提升机偏离原设计中心等进行研究具有较大的工程应用价值。在一般情况下,井塔在混凝土结构的基础上,与井筒没有直接连接,井筒直接坐落在基岩上,因此,井筒整体基本不会发生沉降变形。矿井井塔产生偏斜的原因大致可以分为2 个方面[3]:一方面是井塔基础的不均匀沉降,包括地基土的固结压缩、地下水水位浮动等;另一方面是由于矿井提升量的改变而使井塔部分发生变化。目前井塔纠偏加固方法一般为迫降纠倾和顶升纠倾[4]。刘祖德[5]于1990年提出应力解除法,并用于建筑物的纠偏处理;曾卫等[6]通过对应力解除法的理论研究,将应力解除法应用于井塔纠偏,并解决了徐州某煤矿井塔纠偏问题;况联飞等[7]对斜孔掏土应力解除的影响因子进行了研究,发现钻孔孔排宽度为掏土纠偏的最主要因子,并解决了华东某双向偏斜生根井塔纠偏问题;孔德才[8]通过对接近临界应力状态的井架部分构件的受力状态进行研究,发现改善井架主要构件的受力状态可解决井架偏斜问题,并运用顶升法解决了童亭煤矿主井井架偏斜问题;刘明凯等[9]对土体冻胀融沉对井架偏斜影响进行了分析研究,发现改善地基土的性质可有效解决井架偏斜问题,并采用袖阀管分层注浆+顶升法对丁集矿大型井架进行了纠偏治理;王在泉等[10]在对井架偏斜原因进行工程地质分析的基础上,提出采用壁后注浆微型钢管混凝土桩进行地基处理的方法和工艺;叶书麟等[11-12]于1980年提出采用树根桩加固既有建筑物地基基础,该技术经过发展已成为一项成熟的既有建筑物地基加固技术,目前,树根桩加固长度通常为30 m 左右[13]。树根桩的加固机理如下:由于在成桩过程中采用静压注浆,浆液会在岩土体中充分扩散,一方面,会使原来桩壁与周围土层有空隙的地方被强行压入的水泥浆强制填充,可提高桩侧摩阻力;另一方面,浆液的充分扩散使得桩体与周围土体在一定压力下形成不规则的圆柱状的水泥浆混合体,这一不规则的截面形状将大大增加桩土之间的摩阻力和抗水平荷载的能力。树根桩的施工不仅改变了周围土体的物理力学参数,对周围土体有“挤密”作用,在一定条件下限制了桩间土的侧向位移,而且树根桩的“群桩效应”使得地基土层的稳定性大幅度提高。应力解除法及顶升法在井塔纠偏方面已得到广泛应用,不过在井塔纠偏工程中,以往学者很少关注基础地基加固研究。树根桩加固纠偏法在建筑物纠偏中已形成一套成熟的体系,而人们对其井塔加固纠偏方面的研究与应用较少。树根桩加固纠偏法能否用于井塔的纠偏还需验证。为此,本文作者针对三山岛副井井塔偏斜问题,提出采用树根桩加固纠偏的方法对副井井塔进行处理,并通过理论计算、数值模拟以及现场监测对其可靠性进行验证。
1 工程概况
1.1 工程背景
山东黄金集团三山岛金矿新立分矿位于莱州市北向的三山岛镇,矿区日生产矿石为4 000 t,矿井的服务年限为20 a[14]。副井井筒大致位于井塔偏北侧,井口标高为±0 m,井筒净直径为2.25 m。副井井塔有9 个独立桩基础,桩基础埋深最深为38.7 m,最浅为16.7 m,主要由柱子、承台及桩组成,材质均为钢筋混凝土,且此井塔桩基础未与井壁混凝土刚性相连,为不生根井塔。副井井塔于2018年出现偏斜现象,经实际测量,井塔桩基础西侧目前沉降量约为-15.0 cm,且出现偏斜现象。井塔的偏斜已经严重影响到副井的正常运行,故需查明井塔偏斜的主要原因,并对井塔采取相应的纠偏措施。
1.2 井塔偏斜原因
根据现场勘测初步判定副井井塔偏斜的原因主要如下:一是井塔结构布置的影响;二是原设计摩擦桩长度不一;三是潮汐水的影响。
1.2.1 井塔结构布置的影响
该矿井井筒位于井塔偏北侧(井塔位置如图1(a)所示),这导致井塔在负荷工作时井塔下部桩基础不均匀受力,井塔的重力主要集中在井塔桩基础的西北侧,在该不均匀受力下,下部土层的压缩固结程度不一致,产生不均匀沉降。为了量化分析上部提升机荷载在下部桩基础传递的分布情况,建立结构力学模型进行荷载计算,提升机总质量为100 t,即重力为1 000 kN,提升机距离地面高度约12.0 m,按照9 个桩基础的坐标利用ANSYS 进行建模,可计算提升机荷载在9 个桩基础上的竖向荷载分配值,其中厂房荷载约500 kN。
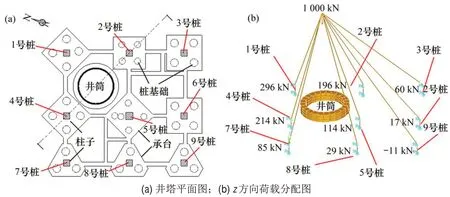
图1 井塔位置及荷载分配示意图Fig.1 Diagrams of auxiliary shaft tower position and load distribution
由图1(b)可知:井塔的西侧受力要比东侧的大,由于承台是一体的,因此,在发生沉降的过程中,上部荷载也会重新进行分配,可以预知沉降量大的一侧将承担大部分荷载。9号桩基础所承担的是向上的拉力,在副井正常工作过程中,这将进一步改变整个桩基础的受力状态。在这种长久的、不均匀力作用下地基土层将不可避免地发生不均匀沉降。因井塔楼发生不均匀沉降,可监测9 个桩基础表面的不均匀沉降量,故将1~9 号桩基础设定为9个沉降监测点。由井塔楼的现状可知:3 号监测点为沉降量最小点,7 号监测点为沉降量最大点。
1.2.2 原设计桩长的影响
原有桩基长度不一,西侧的原有桩基相对东侧桩基长度最大差值为22 m。井塔及地层的剖面图如图2所示。由图2可知:井塔所在的地层主要是砂石层和粉质黏土层,其中粉质黏土层厚度大致是砂石层的5倍。当粉质黏土层上部荷载传递不均匀时,极易在地层中产生不同的附加应力,进而导致土层的压缩固结程度不一致。
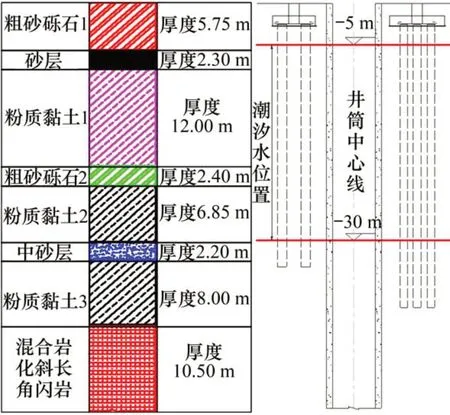
图2 井筒及地层剖面图Fig.2 Profile of wellbore and stratum
1.2.3 潮汐动力水的影响
潮汐动力水对地基土体有冲刷作用,会改变地基土体中的应力条件。冲刷作用会带走地层中的砂粒,并对井塔桩基础造成扰动。由勘察资料可知,井塔位置靠近海边,每天均会有潮汐水对其产生影响。潮汐动力水与静态状况下的主要区别是:潮波是由潮汐引起的海水表面发生的波动现象,一般以类正弦波或余弦波的形式出现,波长会比较长,带有能量的传递[15]。与静水工况不同的是在计算潮汐动力水作用的工况时,需要根据当地潮水的基本信息,在潮汐水作用面添加正弦或者余弦荷载。潮汐水作用位置如图2所示。
2 纠偏方案设计
2.1 井塔桩基础加固设计与分析
针对以上工程概况,本文拟采用树根桩进行井塔加固纠偏,即采用树根桩加固地层的方法对井塔桩基础进行加固,加固后对提升机重新安装定位,以进行纠偏。
采用树根桩加固地基基础后,并不会使原有的地基土应力状态恶化,否则将会使建筑物直接倒塌[16-17]。进行树根桩加固设计时主要依据如下:
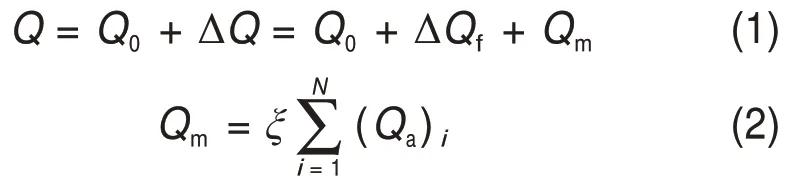
式中:Q为作用的总荷载(kN);Q0为作用的原建筑物荷载(kN);△Q为作用于桩-土地基上的荷载增量(kN);△Qf为作用于地基土的荷载增量(kN);Qm为作用于桩体的荷载(kN);Qa为单桩承载力(kN);ξ为群桩效率系数,当桩间距大于6倍桩径时,ξ取1.0;当桩间距为3~6倍桩径时,ξ取0.8~0.9;当桩间距为2~3 倍桩径时,ξ取0.7;N为树根桩总数量(个)。
树根桩的直径宜为150~400 mm[4],但因冠梁板是根据井塔的位置而进行设计施工的,无法对其宽度进行优化,同时,为防止潮汐水对井塔地基基础的影响,故在冠梁板上至少设计2 排树根桩。
综合考虑现场施工条件、冠梁板的宽度及所加固树根桩的数量,确定树根桩的直径为200 mm;根据现场单桩承载力试验[18]可知设计树根桩单桩承载力为75 kN;因在一定范围内树根桩的长度对其单桩承载力影响不大,根据勘察资料可计算出所需II 型树根桩(II 型树根桩采用水泥浆护壁钻孔施工)约为120 根,因树根桩主要布置在冠梁板上,故其桩间距为3~6倍桩径时可使树根桩近似均匀布置,其群桩效率系数取0.8。为隔绝潮汐动力水对井塔地基基础的影响,在冠梁板外侧设计102 根I 型树根桩(I 型树根桩采用泥浆护壁钻孔施工),其与II 型树根桩交叉施工。树根桩平面布置示意图如图3所示。
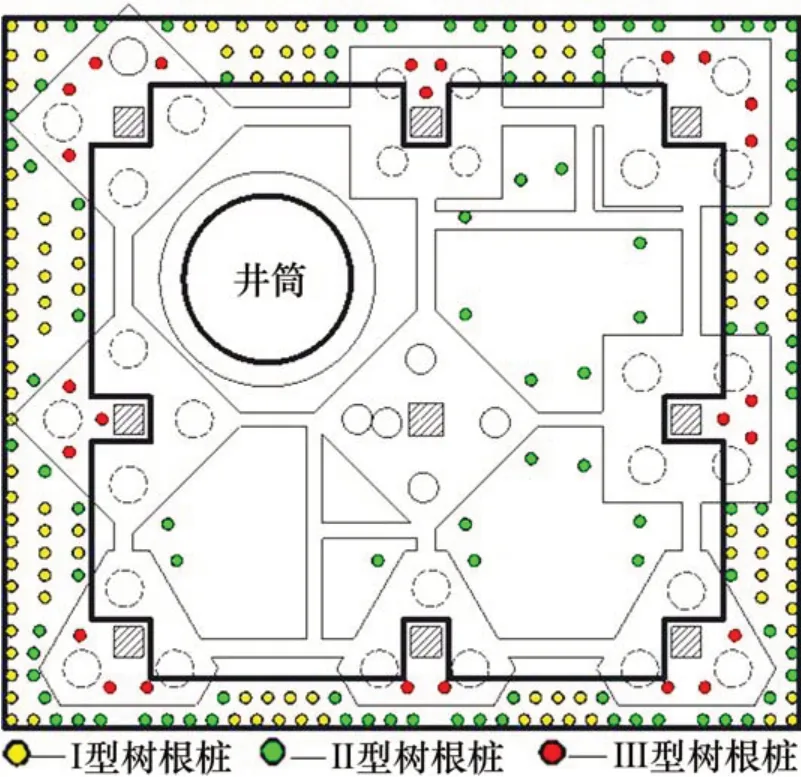
图3 树根桩平面布置示意图Fig.3 Plane arrangement of the root piles
树根桩主要设计原则如下:在原设计摩擦桩周围施工II 型树根桩,与原设计摩擦桩相辅相成,既隔离潮汐动力水,也可起到承担主要竖向荷载的功能;在原设计摩擦桩桩间土位置施工I型树根桩;同时,为保证冠梁板与原设计承台具有联结作用,增设25根III型摩擦桩(III型树根桩长2.5 m,采用水泥浆护壁钻孔施工)。由于井塔西侧比东侧沉降量大,树根桩的总体设置是东疏西密。III 型树根桩为锚固型树根桩,其主要作用是将所有的连梁、冠梁和树根桩与原有的柱子、承台、灌注桩连为一个整体,起到整体联动受力作用。
树根桩施工完成后,按照设计进行放坡开挖沟槽,采用钢筋混凝土施工冠梁和连梁,连梁与原设计柱子进行植筋锚固,提高整体的协调变形能力;在冠梁、连梁混凝土养护强度达到设计要求后,将原提升机拆除进行重新安装从而达到纠偏的目的,并对其进行持续监测,保证副井的正常运转。
在加固纠偏方案的研究中,为对比有水条件下的地基基础加固效果,将增加无水条件下的工况,起参照作用。因树根桩加固长度为30 m 左右时其力学机制较清晰[4],且本文中原设计摩擦桩为37.5 m,故为了更合理安全地研究不同长度的树根桩加固后的效果,所加固用树根桩的长度选取30.0,32.5,35.0和37.5 m进行对比研究。根据“建筑地基基础设计规范”[19]第5.3.4条要求,并考虑工程条件及后期对提升机改造的需求(工程要求树根桩加固纠偏后桩基础竖向沉降量及桩基础偏差量均小于等于10.0 mm),通过理论分析和数值模拟,讨论不同长度的树根桩加固后的效果,得出经济合理、加固效果理想的纠偏方案。
2.2 计算模型
三山岛金矿副井井塔楼原设计桩基础主要由摩擦桩、承台、柱子组成。各土层物理及渗流力学参数如表1所示,计算模型取副井井筒纵向为z轴,长50 m;垂直于z轴的两侧分别为x和y轴,长均为100 m。计算模型的边界条件采用位移约束:上部为自由边界,底部为固定边界,x轴方向为水平位移约束,y轴方向为前后位移约束。潮汐水主要分布位置在z为-30~-5 m处,作用在模型最左侧边界面;初始孔压按照重力场梯度分布,假定模型除上表面及左侧渗透面其余外边界均为不透水边界。FLAC3D数值计算模型如图4所示。
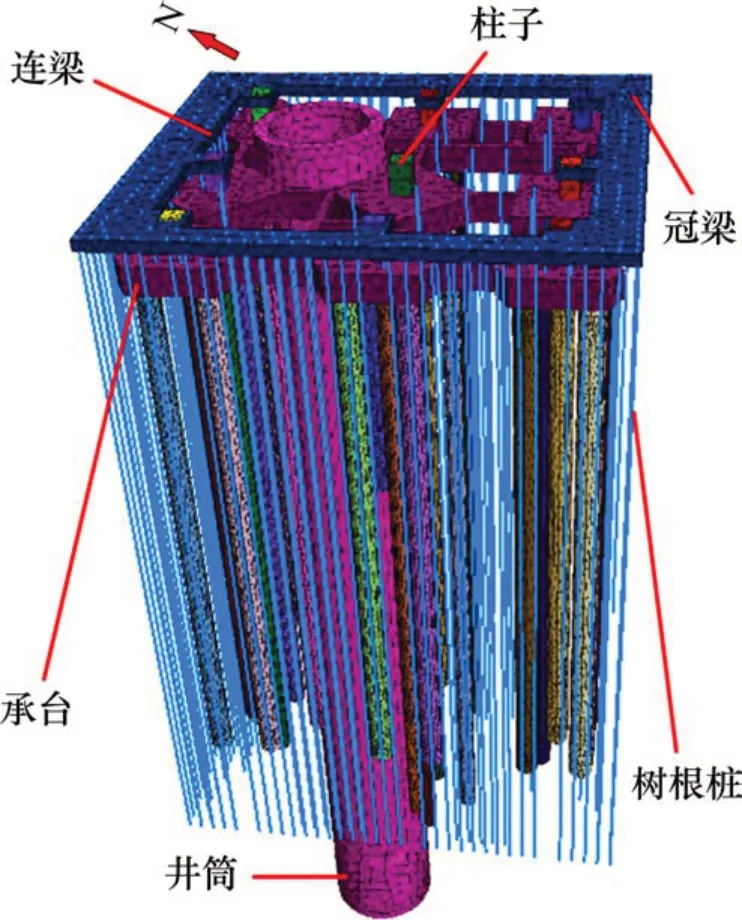
图4 计算模型示意图Fig.4 Diagram of calculation model
因地基加固后x和y方向的位移是次要因素,故本文主要研究桩基础加固后z方向位移。相同地层采用各向同性渗流模型。混凝土弹性模量为34.5 GPa,泊松比为0.2,密度取2 500 kg/m3,土层的孔隙率均取0.5。
2.3 模型验证
结合表1对数值模型的正确性进行检验,按照原设计参数对模型进行相应的沉降监测,现场监测结果与数值计算结果对比如图5所示。由图5可知:二者整体变化规律一致,数值较接近。结果表明该数值模型可以客观地反映在上部荷载和流固耦合作用下桩基础及土体的变形规律,可用于地基加固后变形规律研究。

图5 实测沉降量与数值模拟结果对比Fig.5 Comparison of measured displacement and numerical simulation results
3 桩基础沉降的修正Boussinesq解
目前在工程上应用最为广泛的桩基沉降分层总和计算方法主要有2大类[20]:1)实体基础法,即用Boussinesq解计算土中的应力,然后按照分层总和法计算桩基础的沉降;2) Mindlin 应力计算法,即用Mindlin解计算土中的应力,然后按照分层总和法计算桩基础的沉降。此2 种方法各有优缺点:Boussinesq解适用于浅基础,计算深基础时会有一定的误差,在工程上应用广泛;Mindlin 解适用范围更广,但是其计算过于繁琐。“建筑桩基技术规范”[21]引入桩基等效沉降系数对Boussinesq 计算的桩基础沉降进行修正,使其结果更加接近实际,目前已被广泛应用于地基基础沉降计算中,本文将采用此种方法进行计算,计算简图如图6所示。图6中,F为桩基础上部外部作用荷载;d为承台高度;l为桩的有效长度;f为桩侧摩阻力;a和b分别为承台的长度和宽度;a0和b0分别为群桩的外缘矩形的长、短边长度;θ为应力扩散角;-φ为桩所穿过土层的内摩擦角加权平均值。
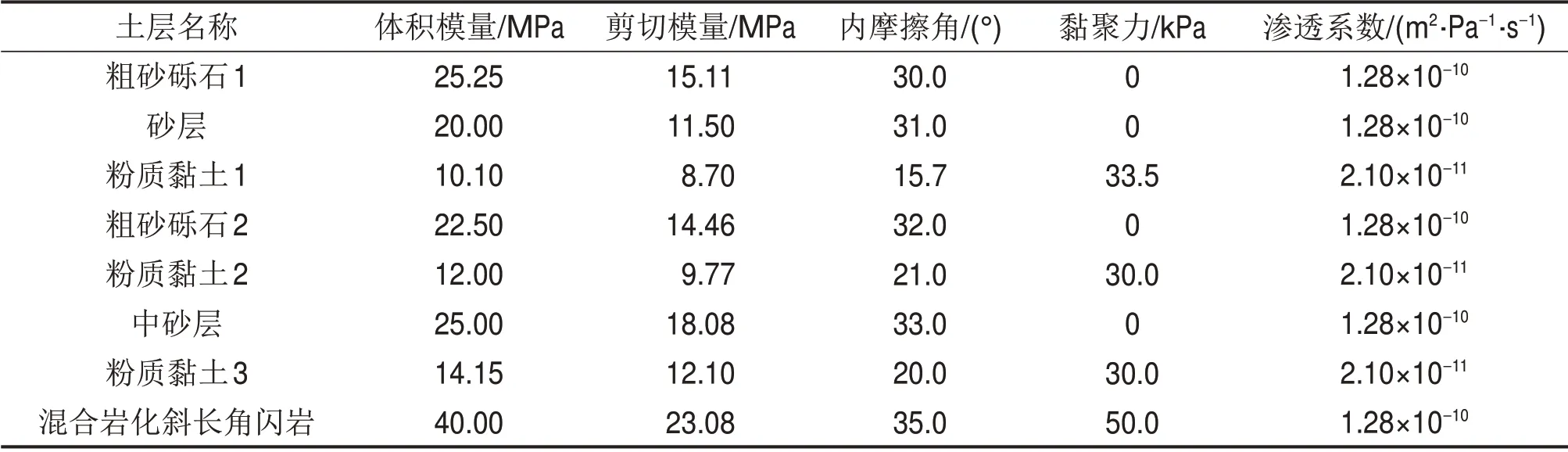
表1 土层物理及渗流力学参数Table 1 Physical and seepage mechanical parameters of soil
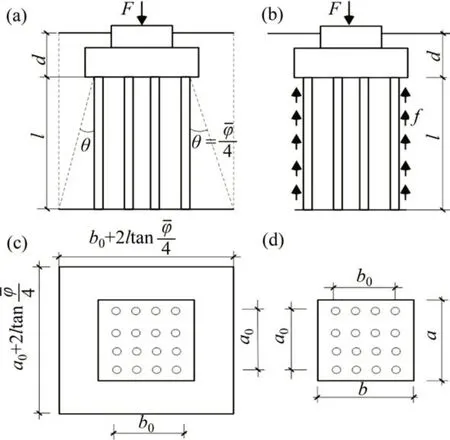
图6 Boussinesq解计算简图Fig.6 Calculation diagram of Boussinesq solution
假设如下:土体为半无限空间弹性体,将桩端平面作为弹性体的表面;地基经过树根桩加固后只存在竖向位移或水平位移可忽略不计。“建筑桩基技术规范”[21]建议,计算矩形桩基础中心点沉降时,桩基沉降量为

式中:s为桩基最终沉降量(mm);s′为采用Boussinesq解,按实体深基础分层总和法计算出的桩基沉降量(mm);ψ为桩基沉降计算经验系数;ψe为桩基等效沉降系数;n为桩基沉降计算深度范围内所划分的土层数;p0为在荷载效应准永久组合下承台底的平均附加压力(kN);Esi为作用面以下第i层土的压缩模量(MPa);zi和zi-1为桩端平面至第i层土、第i-1层土底面的距离(m);和分别为平均附加应力系数。
基底附加应力p0按照式(4)进行计算:

式中:G为承台和承台上土的自重(kN);pc0为承台底面高程处地基土的自重应力(kPa)。
桩基等效沉降系数ψe可按下式进行计算:
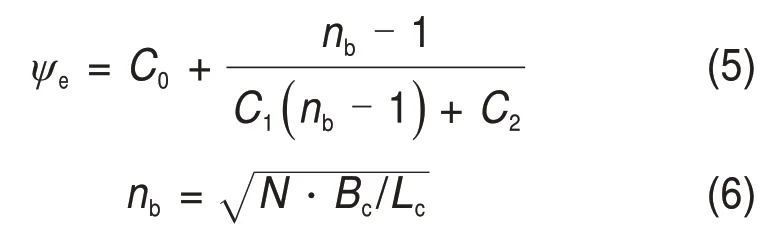
式中:nb为矩形布桩时的短边布桩数(个);C0,C1和C2为沉降系数计算参数,按照“建筑桩基设计规范”[21]附录E确定;Lc和Bc分别为矩形承台的长(m)和宽(m)。
因树根桩加固密度较大,故将其看作是1个承台,其承台埋深d=3 m,取有效桩长l分别为27.0,29.5,32.0和34.5 m,提升机荷载为1 000 kN,a,b,a0和b0近似相等,均赋值为20 m,根据表1物理力学参数可计算出在桩穿过土层的内摩擦角加权平均值分别为21.7°,22.2°,22.0°和20.2°,可计算出基底附加应力p01=39.59 kPa,p02=37.78 kPa,p03=36.58 kPa,p04=36.78 kPa,无水条件下计算步骤与之相同。
根据修正后的Boussinesq解可分别计算出有水条件下4 种桩长的z方向沉降,其相关计算参数见表2。由表2可知:有水条件下,这4 种工况计算所得的桩基础沉降量绝对值均小于10 mm,满足基本要求;但采用桩长为35.0 m及37.5 m的2种加固方案对井塔地基基础进行处理后,地基基础沉降绝对值均小于3 mm,可知其加固性能非常优异;桩长为30.0 m及32.5 m的2种加固方案对井塔地基基础进行处理后,地基基础沉降绝对值均大于5 mm且小于10 mm,其加固性能较优异。
对比分析解析解所计算出的地基基础沉降量可初步判断:桩长为35.0 m 及37.5 m 的树根桩加固方案对于地基加固效果较优,但未能充分发挥地基基础的承载力;桩长为30.0 m 及32.5 m 的树根桩加固方案既满足设计要求,同时也使得地基基础的承载力得到充分发挥。
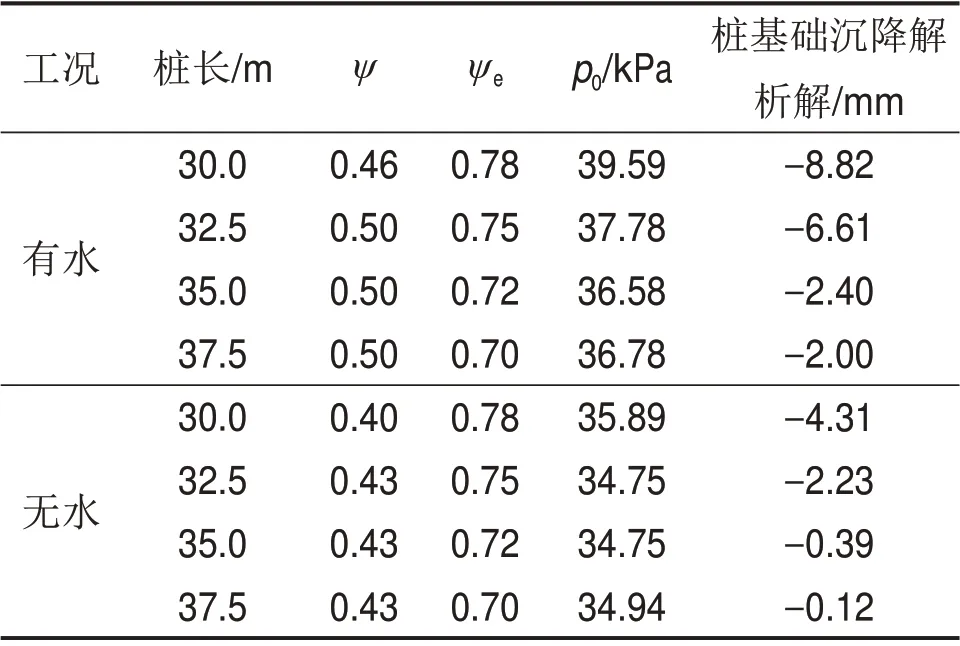
表2 桩基础沉降的修正Boussinesq解Table 2 Corrected Boussinesq solution for foundation settlement
4 桩基础沉降的数值分析
为了进一步研究9个桩基础在加固纠偏后的残余沉降,通过数值模拟对解析解进行进一步对比研究。通过在9个桩基础顶点设立观测点,可较为直观地观察在荷载和地下水作用下桩基础z方向的变形规律。由计算结果变形沉降云图(见图7和图8)可以看出:在不考虑地下水时,井塔桩基础沉降主要由上部荷载以及地应力场决定,不同长度的树根桩加固后各个桩基础顶点的沉降差别不是很大。相较于无地下水工况,有水工况下井塔桩基础沉降不仅受上部荷载和地应力场的影响,同时流体也会对其造成明显的影响,井塔桩基础各个桩的沉降量明显增大,涨幅近100%,各桩顶点沉降规律基本一致。且随着树根桩加固桩长增加,虽然井塔西侧仍表现出一定的不均匀沉降性,但此现象越来越不明显。
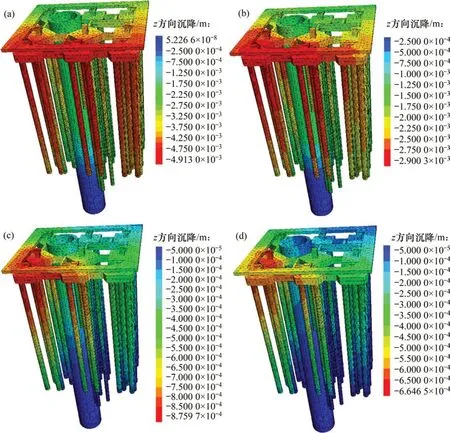
图7 无水条件下加固后z方向沉降云图Fig.7 Displacement cloud map in z direction after reinforcement under waterless conditions
表3所示为有水、无水2种工况加固后井塔桩基础沉降量绝对值的最大和最小值对比。由表3可知:其最小与最大沉降量绝对值的差值均未超过10.0 mm,其差值随着加固桩长的增大而减小,地基基础的稳定性得到提高。
数值模拟结果显示:一方面,随着树根桩长度的增加,施工后的地基基础沉降量随之变小;另一方面,潮汐动力水对地基基础沉降量有一定的影响。此结果在很大程度上验证了前文中对井塔偏斜原因分析的合理性。

表3 加固后的桩基础最大与最小沉降量Table 3 The maximum and minimum settlement of pile foundation after reinforcement
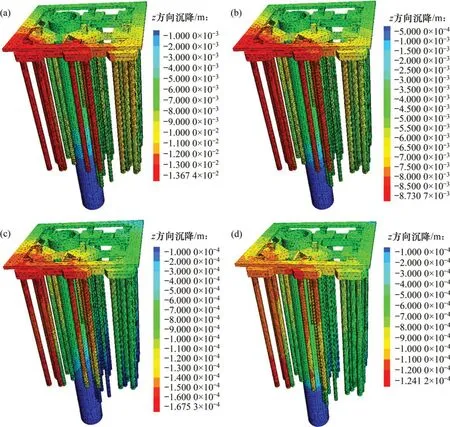
图8 有水条件下加固后z方向沉降云图Fig.8 Displacement cloud map in z direction after reinforcement under water conditions
图9所示为无水和有水2种工况加固后沉降量对比图。通过对比流固耦合作用下不同长度的树根桩加固后9个桩基础顶点的沉降量变化曲线可以发现,有水工况下桩长为30 m 的树根桩加固效果不是太理想,其最大沉降量绝对值达到13.0 mm,最小沉降量绝对值为7.1 mm,不符合加固地基后最大沉降绝对值在10.0 mm 内的要求;长度为35.0 m与37.5 m的树根桩加固后,其效果卓越,最大沉降量绝对值为1.5 mm,虽然加固效果很好,但是从经济角度看不太合理,且没有完全发挥地基土的承载能力;长度为32.5 m 的树根桩加固效果较理想,其最大沉降量绝对值为8.2 mm,最小沉降量绝对值为4.3 mm,既在沉降允许范围内,又使得地基土的承载能力得到充分发挥,实现了经济合理、加固效果显著的目的。
将无水条件下的数值解(图9(a))与表2中的无水工况解析解进行对比可以发现:对于同等加固长度的树根桩,无水条件下的解析解数值与数值解数值较接近,但均特别小。如桩长为30.0 m时,解析解为-4.31 mm,数值解(即9 个桩基础沉降量的平均值)为-4.00 mm;由于无水条件下的桩基础沉降量太小,4种加固桩长的桩基础沉降量绝对值最大仅为4.31 mm,表明在研究过程中若不考虑地下水的作用,则对研究结果将会造成很大的影响。
将有水条件下数值模拟的9个桩基础沉降取平均值与解析解进行对比分析,结果如图10所示。采用桩长为30.0 m 的树根桩加固方案对地基基础进行处理后,虽然桩基础工后残余沉降的平均沉降量达到了设计要求,但仍有部分井塔桩基础沉降量绝对值超过10.0 mm;采用桩长为32.5 m的树根桩加固方案对地基基础进行处理后,通过观测9个桩基础沉降量可知,井塔桩基础的沉降量绝对值均未超过10.0 mm,且通过修正Boussinesq 解得到的桩基础沉降量与数值模拟得到的桩基础平均沉降量在数值上近似相等,说明针对本文中的工况选取32.5 m 的树根桩进行加固具有合理性及适用性,同时也表明树根桩可以应用于井塔纠偏等类似工程中。
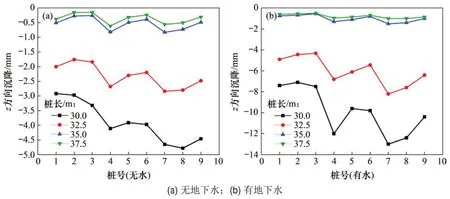
图9 无水及有水加固后z方向沉降对比图Fig.9 Displacements comparison in z direction after reinforcement under waterless and water conditions
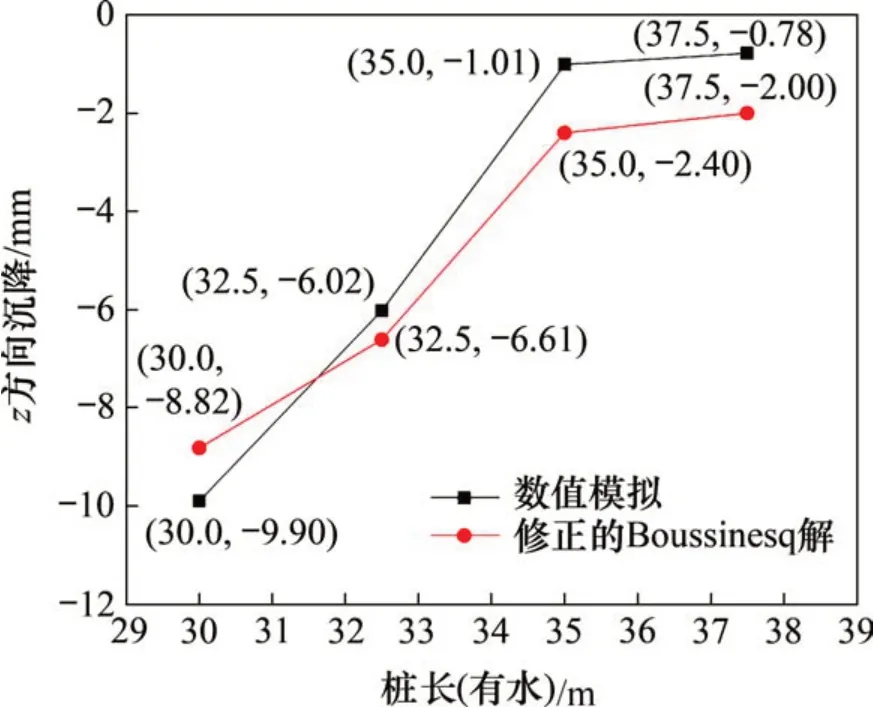
图10 z方向沉降数值模拟与Boussinesq解对比Fig.10 Comparison of numerical simulation and Boussinesq solution of displacements in z direction
由图10可以看出:随着桩长增加,z方向沉降数值模拟结果的绝对值略小于理论计算结果的绝对值。这与解析解的假设条件、数值模拟的计算方法有一定的关系,解析解在计算过程中忽略了水平位移,即只考虑了桩下土层的压缩。而数值模拟是基于有限差分算法,通过网格节点进行推导计算,在树根桩发生竖向沉降的过程中,因桩体的网格和岩土体的网格有一定的耦合作用,故在树根桩发生竖向沉降的过程中,周围岩土体会在一定程度上阻碍树根桩的竖向沉降,这使得同等计算条件下的数值模拟结果的绝对值略小于理论计算结果的绝对值。
5 结论
1)采用修正的Boussinesq解可以很好地用于计算桩基础沉降,且计算结果显示4种工况所得的桩基础沉降量绝对值均小于10.0 mm,满足加固纠偏要求。
2)相较于不考虑地下水的影响,在流固耦合模型中,加固后桩基础的沉降变化规律基本一致,但整体竖向沉降量明显变大,平均增幅达100%,可知渗流应力场的作用比较明显,在进行含地下水工况的地基加固设计中,水的作用不可忽略。
3)树根桩的桩长与加固后桩基础的沉降呈负相关关系。随着桩长增加,加固后的桩基础沉降量逐渐变小。故在设计树根桩桩长时,要考虑充分发挥地基土的承载能力,使加固方案具有准确性和可靠性。
4)基于流固耦合理论进行数值模拟沉降计算,对计算所得的修正Boussinesq解数值进行验证,发现当解析解计算结果满足要求时,部分桩基础的沉降量可能不满足要求。同时也表明树根桩加固纠偏方案具有经济合理性,可广泛应用于井塔纠偏工程中。

