一种变工作空间并联机构的设计及应用
(北京交通大学机械与电子控制工程学院,北京,100044)
在以往对并联机构的研究中,由于其各自的固有结构特性,机构的工作模式和工作空间一般固定。但随着其应用背景的扩展,如在工业生产领域,同一机构在固定的安装位置通常需满足零件安装、箱体分拣、转移运输等不同任务要求。对于这种使用需要,学者们基于不同理论提出了拥有大工作空间的并联机构构型[1-4]。GOSSELIN等[5-6]分别对内部无奇异大工作空间和大转角少自由度并联机构进行了分类。LI等[7]还提出了一种能够全周转动的并联飞行模拟器运动机构,通过大工作空间体积来覆盖不同的目标任务。但当所需各项任务集中在某一特定工作区域时,其他区域工作空间则无法得到有效利用,致使机构的工作空间利用率降低,加快机构驱动关节的局部磨损速度,降低机构使用寿命。因此,学者们提出以变工作空间结构形式实现多工作空间叠加与扩展,间接增大工作空间体积。对比传统的固定结构,变工作空间机构可根据不同任务需求重构自身结构,满足任务需求的同时提高工作空间利用率。COPPOLA 等[8-10]通过改变驱动关节方向、调节支链与基座连接位置及动平台结构的方式进行机构的结构重构。HUANG 等[11-12]在机构中加入了被动支链、齿轮、轮系等结构,并通过锁定和释放相应的关节,达到改变动平台运动形式的目的。FU等[13-16]根据运动学反解,将不同的驱动方案定义为多种工作模式,通过叠加不同工作模式下的工作空间,实现了工作空间覆盖面积的间接增大。虽然通过重构自身结构可实现工作空间的变化,但上述研究中采用的复合运动副和锁闭关节会使各支链的转动惯量增大,降低对应结构的并联机构实际使用可靠性,增加机构的驱动器质量和控制难度。针对上述问题,本文作者基于一种平台演化思想提出一种新型变工作空间并联机构,在动/定平台中分别加入转动副,引入机构结构角来实现工作空间的变化,且结构角所在关节远离驱动及运动支链,增加了机构的运行可靠性。冗余驱动支链的使用增大了机构运动的稳定性,有利于工作空间内部任务轨迹规划的进行。建立含自由度、位置解、雅克比、奇异性的运动学模型,完成包括工作空间、灵巧度、刚度在内的性能分析,并针对特定任务背景进行机构的应用分析。
1 机构的提出及自由度分析
1.1 平台结构的演化
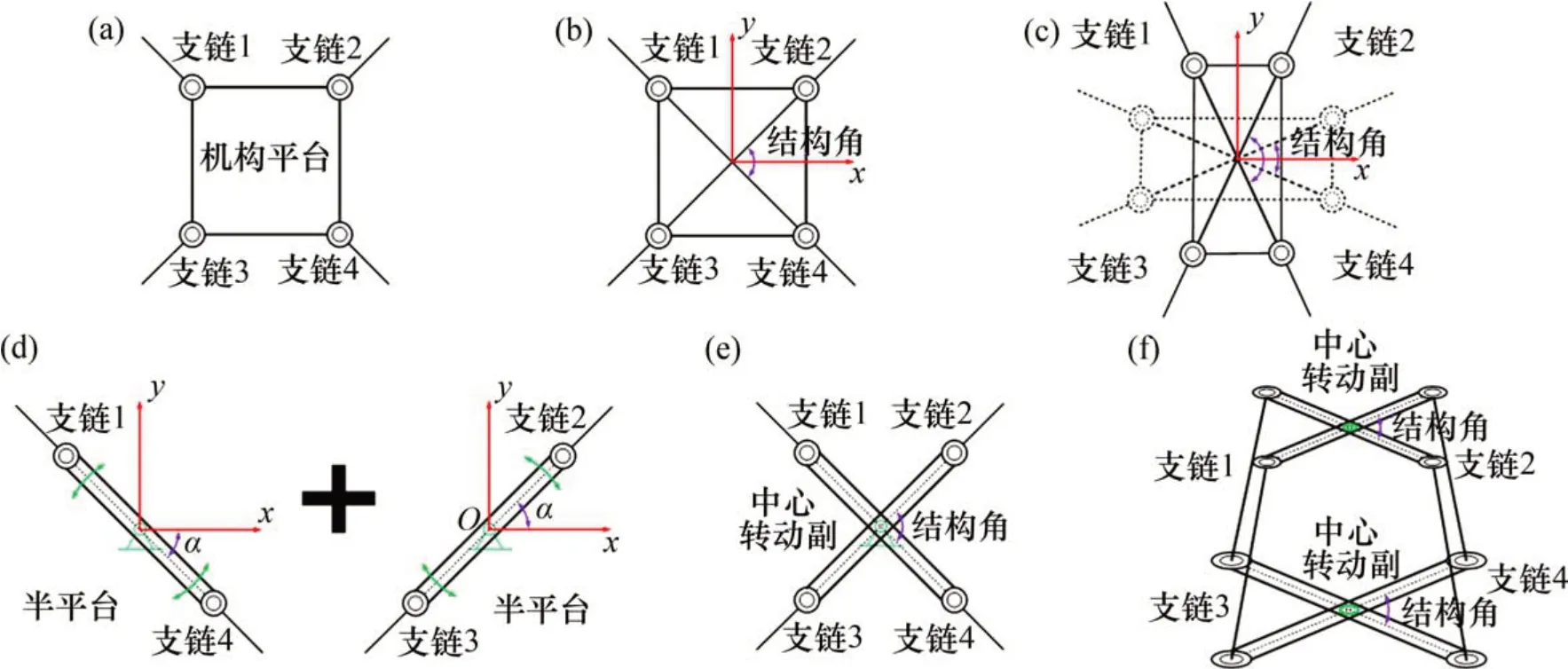
图1 一类变工作空间并联机构结构演化示意图Fig.1 Structure evolution diagram of a kind of parallel mechanism with variable workspace
为实现变工作空间的目的并避免增大运动支链及运动副的质量,可采用改变动/定平台结构尺寸的思路以实现机构尺寸的重构,从而实现机构工作空间的变化。图1(a)所示为一种传统固定尺寸四运动支链并联机构的平台结构。如需改变该四边形平台的结构尺寸,可改变四边形对角线夹角以实现四边形边长的变化,如图1(b)~(c)所示。根据此思路,可将固定尺寸动平台演化为2个尺寸相同的直线状半平台,在半平台中点加入转动副以进行组合,演化过程如图1(d)~(e)所示,其中,转动副命名为“中心转动副”,两半平台夹角命名为机构的“结构角”。以这种演化平台结构作为动/定平台,并以相应的运动支链相连,即可构建为一类变工作空间并联机构,如图1(f)所示。在该结构下,不但可实现机构结构尺寸和工作空间的变化,且中心转动副距运动支链距离较远,减小了机构整体转动惯量,提升了可靠性。
1.2 可变工作空间并联机构的提出
根据平台结构演化思想提出一种可变工作空间并联机构,其结构简图和矢量分析图如图2所示。该机构包括一个含中心转动副(R)的动平台和定平台,4条UPU(分别为万向副U、移动副P、万向副U)运动支链,故根据结构特点可命名为4UPU-R 并联机构。上下平台结构类似,均由2 个带有转动关节的半平台组成,其中上下平台中半平台的万向副转动轴线之间的连线长度相等,即A1A3=A2A4=2r,C1C3=C2C4=2h(其中r和h分别为定平台和动平台所在外接圆半径)。半平台之间依靠各自的中心转动副连接。在调整中心转动副时,保持上下结构角相等,即A1A3∥C1C3,A2A4∥C2C4。上下平台的中心转动副在机构工作过程中保持锁定,在工作前根据任务要求调整所需角度。上下平台上对侧万向副轴线平行,4条运动支链结构与尺寸参数相同。在实际使用过程中,定平台为机构下平台,动平台为机构上平台,机构各支链中的移动副驱动值即支链长度为输入量,输出量为动平台中心点在空间的参考位置。设定平台和动平台的中心点O与O′分别为机构定坐标系与动坐标系的原点,两坐标系的z轴分别与动/定平台所在平面垂直,x轴分别沿∠C2O′C3和∠A2OA3角平分线方向,则y轴可根据右手定则确定。坐标轴方向及其余参量如图2所示,其中,设半平台与x轴夹角为α(即结构角的1/2),各驱动支链长度|CiAi|为li(i=1,2,3,4)。值得一提的是,赵铁石等[17]也曾提出过一种以UPU 为支链结构的4UPU 并联机构,该机构通过与本文机构不同的U 副角度,使得其动平台可实现空间三移动一转动自由度。但与本文机构不同的是,4UPU机构动平台不具有工作空间可变性。而本文的4UPU-R并联机构通过加入中心转动副,在实现动平台工作空间可变性的同时,增加了机构在实际使用过程中的多任务应用可行性。
1.3 自由度分析
由于机构在工作过程中,中心转动副处于锁定状态,故在自由度计算时不考虑该运动副。4UPU-R并联机构各运动支链结构相同,使用螺旋理论,选择1 条UPU 支链建立局部坐标系进行运动和约束螺旋分析。局部坐标系x和y轴与定平台端U 副两轴线方向相同,z轴沿移动副轴线方向。设两万向副距离为a,则支链运动螺旋为
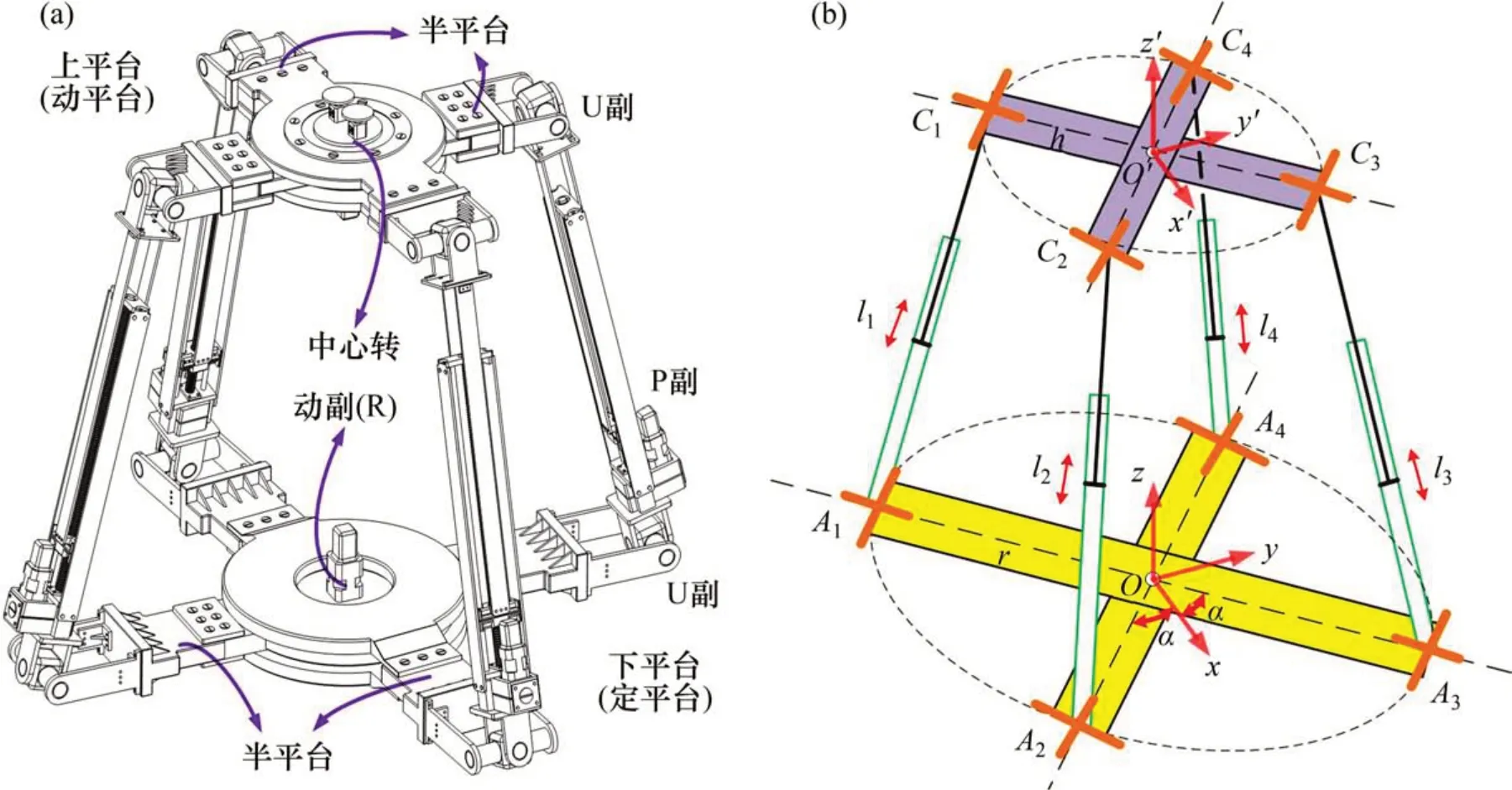
图2 4UPU-R并联机构结构简图Fig.2 Sketch of 4UPU-R parallel mechanism

式中:$i(i=1,2,3,4,5)为运动螺旋。该支链的约束螺旋式即为式(1)所示各运动螺旋$i的反螺旋即$r=[0 0 0;0 0 1]T,方向沿移动副轴线方向,见图3(a)左图。
对机构整体而言,各支链对动平台提供的约束为一沿该支链移动副轴线方向的约束力偶$ri(i=1,2,3,4),如图3(a)右图所示。机构整体约束螺旋系由4个互不平行的纯约束力偶组成,易得螺旋系秩为3[18],代入自由度M计算公式:
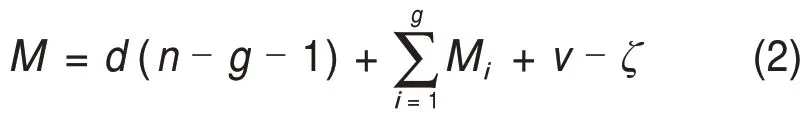
式中:机构阶数d=6-λ,λ为机构公共约束数;n为机构总构件数;g为机构总运动副数;Mi为第i个运动副的自由度数,对于本文机构,i=1~12;ζ为机构局部自由度数;v为除去公共约束后的独立冗余约束数,且v=t-e,其中,除去公共约束后剩余的约束螺旋数为t,除去公共约束后剩余约束螺旋所构成螺旋系的秩为e[16]。则4UPU-R 并联机构自由度M=3,其自由度性质为空间沿x,y和z轴的纯移动。为验证机构动平台的运动性质,使用3D打印技术制作了简易构型样机,图3(b)所示为该机构的3D 打印样机,动平台的运动方向如箭头所示。由于样机为验证性质,故省去了结构角部分。通过该构型样机验证了机构运动的性质,为分析模型的建立提供了依据。
2 运动学分析
2.1 变工作空间并联机构分析模型
根据1.1节所建立的坐标系,可得出定坐标系下Ai及动坐标系下Ci的坐标:Ai(mirc,nirs,0),C'i(mihc,nihs,0);其中,c=cosα,s=sinα,mi=-sin(iπ/2)-cos(iπ/2),ni=-sin(iπ/2)+cos(iπ/2),i=1,2,3,4。通过坐标变换,可将点Ci在动坐标系下的坐标值转换到定坐标系中:
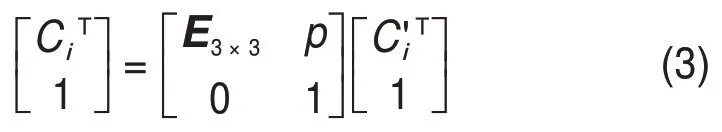
由于机构动平台的运动性质未涉及旋转,故式(3)中E3×3为单位矩阵,动坐标系原点O′在定坐标系中的坐标由p表示。则4UPU-R 并联机构的杆长即支链长度li约束方程为
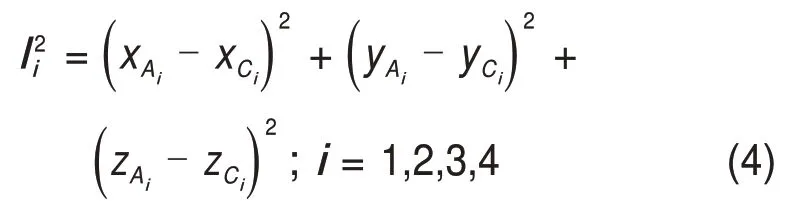
2.2 运动学位置正反解
对于4UPU-R并联机构,其位置反解为已知动平台中点O′坐标(x,y,z),求解驱动支链长度li(i=1,2,3,4)的过程。则由式(4)易得机构的位置反解如下:
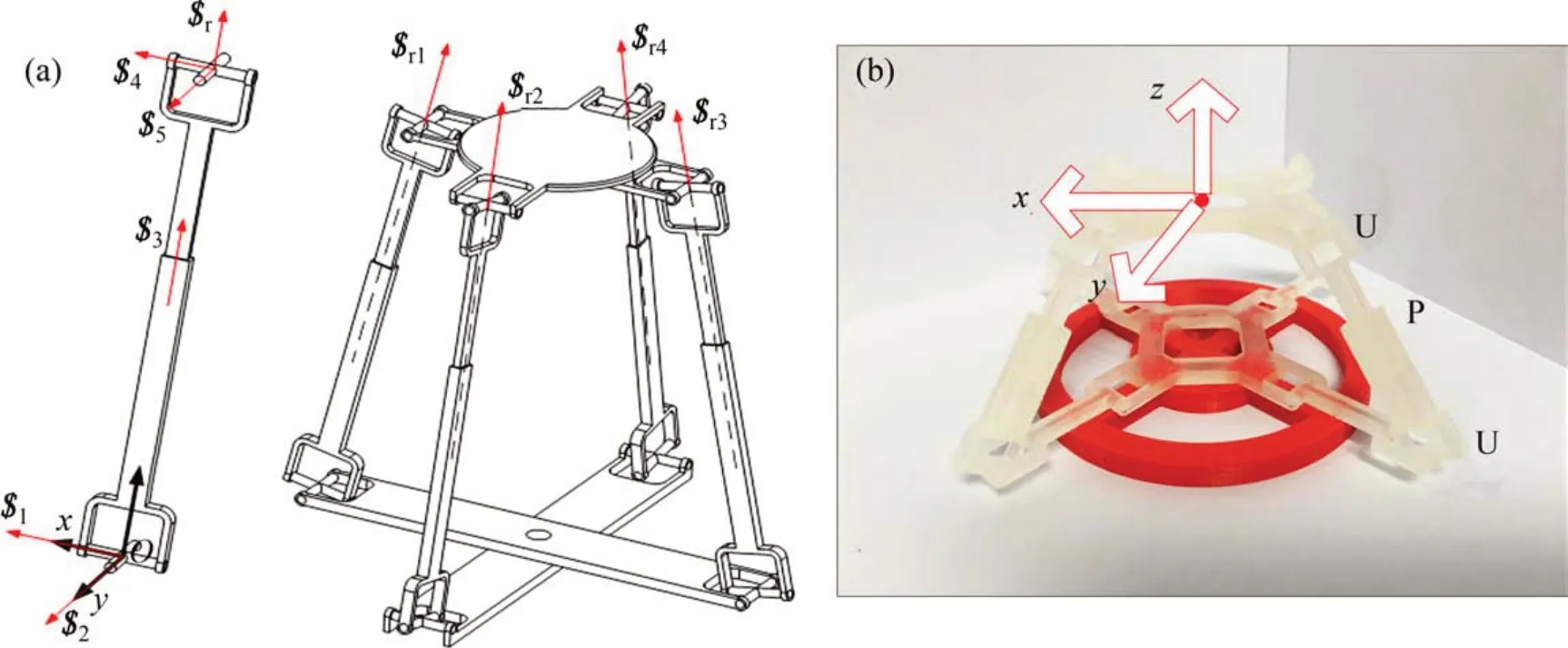
图3 4UPU-R并联机构自由度分析模型及验证样机Fig.3 Degree-of-freedom analysis model and 3D printing prototype of 4UPU-R parallel mechanism
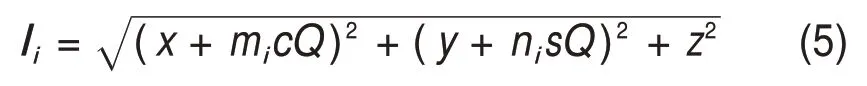
式中:Q=h-r。而4UPU-R 并联机构的位置正解为已知各驱动支链长度li,求解动平台输出参考点O′坐标(x,y,z)的过程。首先可消去y和z得到x的表达式,故以i=1和2先后代入式(4)并将等号两端多项式分别相减,可得:
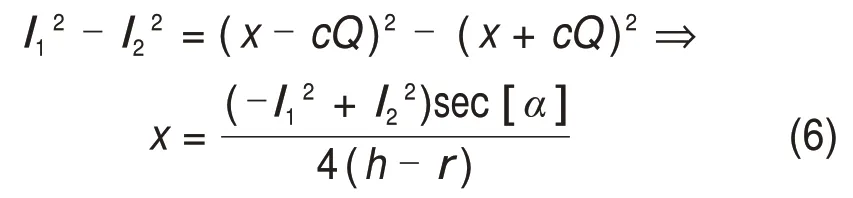
同理,将i=1,4代入式(4)得到y的表达式:
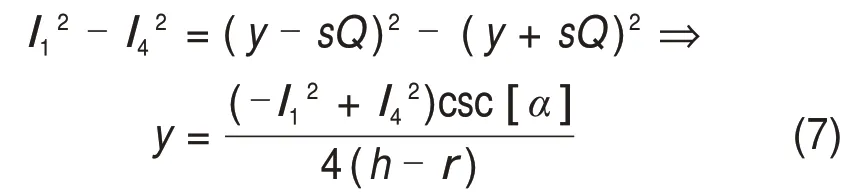
则z可由式(6)和(7)代入式(4)(i取1~4)中解得,其中σ为含h,r,α,li的多项式。

2.3 雅克比分析
并联机构输出参考点速度与输入驱动速度的关系可由雅克比矩阵计算得到[19]:设q为驱动输入参数,x为动平台输出参数,则有JF=JI,其中和分别为输入与输出参数对时间的导数。故输出参数与输入参数间的关系式为=,其中J=F为全局雅可比矩阵;JF为正雅克比矩阵;JI为逆雅克比矩阵。利用含有x和q的机构约束方程f(x,q)分别对输入和输出参数求导可得到4UPU-R机构JI与JF的表达式如下:
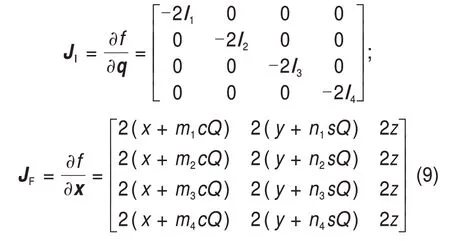
2.4 奇异性分析
由于机构可能存在的奇异位型会使机构产生自由度突变,在实际使用时会给机构本体和操作人员带来极大安全隐患。因此,对机构进行奇异性分析是评价其安全性的重要步骤。本文使用雅克比矩阵降秩法来求解机构的奇异位型[19]。计算不同雅克比矩阵的行列式值,可得到3种不同的奇异情况,即驱动奇异|JI|=0、约束奇异|JF|=0、混合奇异|J|=0。
将式(9)中4UPU-R并联机构的正、逆雅克比矩阵代入,以计算3种奇异情况。由于驱动支链长度li不可能为0,而|JI|=16l1l2l3l4,故该机构不存在驱动奇异。JF为4×3 矩阵,该矩阵行列式不存在,这里任取JF中的3行元素组成3×3的子矩阵JF1,对JF1进行行列式计算,则有|JF1|=8(4h2zcs-8hrzcs+4r2zcs)=0,解得h=r。即当上下平台尺寸相同时,机构发生约束奇异和混合奇异,此时机构的自由度增加,动平台可进行非期望转动。为避免奇异情况,只需在制造该机构时使上下平台尺寸不同即可,即h≠r。当h≠r时,正、逆雅克比矩阵行列式均不为0,故4UPU-R 并联机构不存在奇异位型。
3 性能分析
3.1 工作空间分析
驱动关节(移动副)的驱动范围、被动关节(万向副)的运动范围、结构角的取值、动/定平台的尺度限制、运动支链/平台间的干涉是影响4UPU-R并联机构工作空间的主要因素。下面以点云的形式对该并联机构不同结构角下的位置工作空间形状及覆盖面变化情况进行研究。
首先设定机构结构参数如下:h=135 mm,r=230 mm;驱动范围为310≤li≤430 mm,i=1,2,3,4。选取30°,50°,70°和90°这4个结构角,即α=15°,25°,35°和45°,并分别以不同颜色点云图在同一视图中的z=0,300,600,900 mm 区域输出,如图4所示。其中图4(a),(b)和(c)所示分别为三维点云及沿x-z,y-z平面投影视图。
如图4所示,工作空间整体形状呈伞状,随着结构角的增大,形状会由狭长变为菱形状,工作空间的变化间接增加了机构整体的工作空间覆盖区域。且不同工作空间对应不同任务,也增大了工作空间的利用率。另外,4UPU-R并联机构的工作空间没有因为结构参数的不同而产生畸变,整体较为平滑且不存在内部空洞。
3.2 灵巧度及刚度分析
并联机构的运动精度及稳定性主要由灵巧度与刚度反映,二者都是衡量动平台运动性能的重要指标。并联机构灵巧度和刚度分别以刚度矩阵条件数和最大特征值作为度量标准。其中,刚度矩阵K表达式[8]如下:
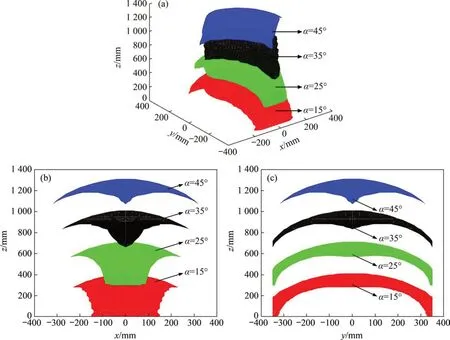
图4 不同结构角的4UPU-R并联机构工作空间Fig.4 Workspaces of 4UPU-R parallel mechanism with different structure angles

式中:驱动关节刚度矩阵KJ=diag[h1,h2,h3,h4],由于该机构驱动关节均为移动副,故取hi=100 kN/m[9],i=1,2,3,4。刚度矩阵的条件数k的计算方法如下[9]:

式中:λmin和λmax分别表示刚度矩阵的最小和最大特征值。
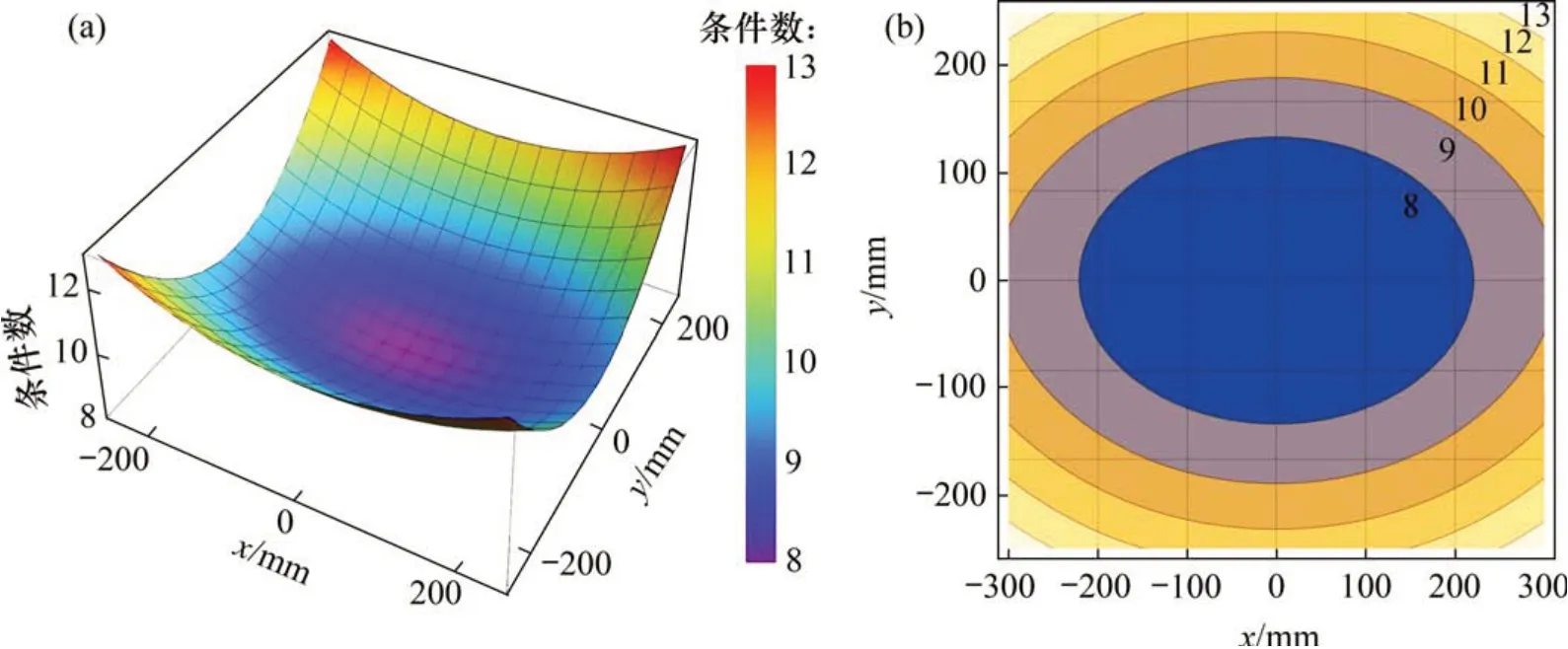
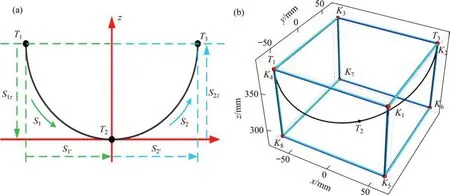
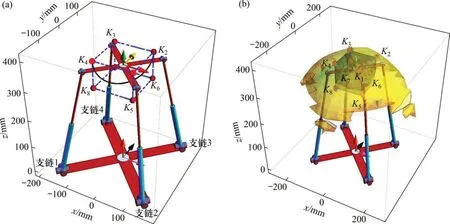
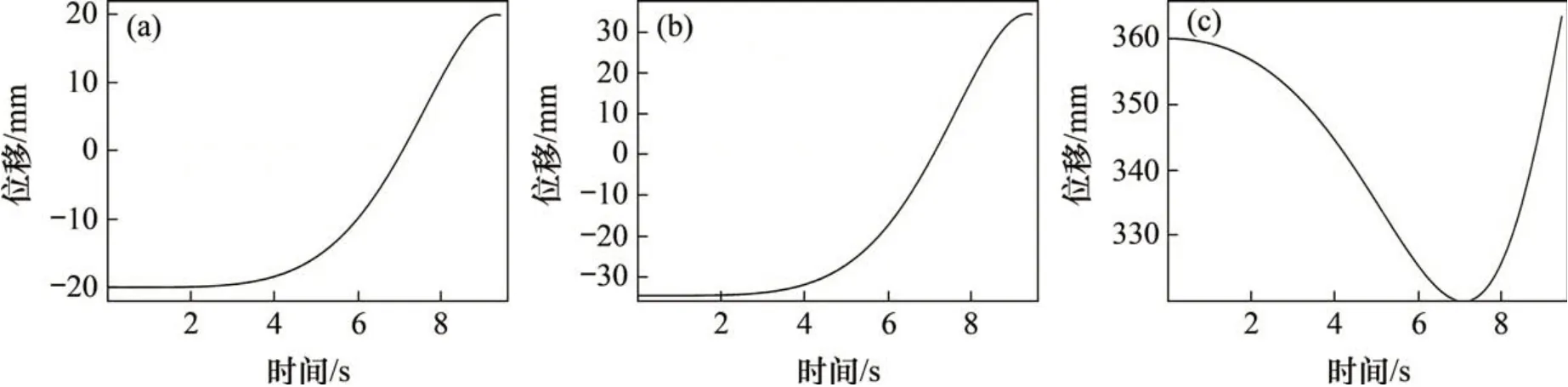
当结构角为60°(α=30°),z坐标为350 mm时,刚度矩阵条件数分布状况如图5所示。从图5可以看出,条件数低值区域(8 同时,选取不同z输出机构所在工作空间平面的全局刚度分布图,分别如图6和图7所示。可见,随着z的增大,4UPU-R 并联机构在给定工作空间内的全局刚度逐渐减小,但整个工作区的刚度平均值可以达到500 kN/m,且呈现工作空间横截面内中间高边缘低的趋势,符合机构正常使用习惯,完全可以适应不同的工作任务。 4UPU-R并联机构可改变自身结构参数以适应不同任务的特性,而结构参数的改变是通过机构自身结构角的变化来完成。该特性可使机构以最小的工作空间体积包络任务所需区域,提高工作空间的利用率。以机构需拥有多重任务适应性为目标,本文提出一种基于运动学解算确定结构角的方法,其流程图如图8所示,具体步骤如下: 图5 z=350 mm时的条件数分布Fig.5 Condition number distribution when z=350 mm 图6 不同z下的刚度分布情况Fig.6 Stiffness distribution along different cross sections 图7 不同z下的刚度分布比较Fig.7 Stiffness distribution comparison along different cross sections 1)根据给定的任务轨迹,以一长方体或球体等规则立体图形包络任务轨迹,以该规则立体图形为任务工作空间区域; 2)在任务工作空间表面选取关键点,关键点的选取原则为:动平台中心在处于该点时,至少1个驱动处于极限驱动值,即动平台中心点处于关键点时,至少1 条运动支链的长度为最大或最小值; 3)动平台位于每个关键点时,将该点坐标及对应的驱动长度li代入杆长约束方程式(4)中,解出相应的一组α; 图8 结构角确定流程图Fig.8 Schematic diagram of structure angle determination 4)最终α的选取原则如式(12)所示: 其中:n为关键点总数;αj为第j个α的取值;Vp为α=p时的实际工作空间体积;α1≤p≤αn。对比验证机构实际工作空间对任务工作空间的包络特性。若机构实际工作空间不能完全包络任务工作空间,则在未包络区域适当加入关键点,再次重复步骤1)和2)。 由于4UPU-R并联机构的固有结构特性,当结构角为90°(α=45°)时,机构实际工作空间体积达到最大值。故当步骤3)得到的计算结果中存在α=45°这一情况时,可直接确定α为45°;当结果中不存在α=45°这一情况时,可根据式(12)进行判定。 下面以实例说明结构角确定方法的合理性。针对工业生产线箱体分拣运输等应用背景,设任务为抓取放置类弧轨迹。任务示意图如图9所示,其中曲线为执行分拣的任务轨迹。首先对该任务轨迹进行运动区域划分,见图10(a),在任务轨迹中标定3 个点位T1,T2和T3,其中T1和T3分别为该抓取放置轨迹中的抓取点和放置点,T2为轨迹中点。设定T1→T2段轨迹为S1,T2→T3段轨迹为S2,S1与S2在z方向和x-y平面上的分量分别为S1z,S2z和S1′和S2′,方向如图10(a)所示。标定点坐标为:总运动时间为9.5 s,机构参数与第3节中的相同。 图9 箱体分拣应用示意图Fig.9 Diagram of box sorting 接下来选择一长方体对任务轨迹进行包络,T1与T3点位于长方体上平面对角线两端点,T2位于下平面中心点,则任务工作空间建立完成,见图10(b)。如机构实际工作空间需完全包络任务工作空间,则该长方体顶点需位于工作空间表面或内部,故将长方体顶点设置为关键点K1~K8。确定关键点后,根据给定步骤计算α,以K2和K8点为例,当动平台中心点位于K2和K8时,支链1 驱动长度应分别取最大和最小值,同理,将各关键点坐标和对应驱动支链长度代入式(4)可解出一组α,计算结果如表1所示。鉴于任务区域与构型的关系,每条支链只需计算使之达到最大和最小驱动值的关键点对应的α即可。图11(a)所示为机构与任务工作空间的相对位置,也表现了各支链与关键点间的对应关系。 根据4.1节中的选择原则,最终确定α=45.37°,此时的机构实际工作空间对任务工作空间包络示意图如图11(b)所示,可见实际工作空间可实现对任务工作空间的完全包络。以上分析过程可看出,该方法可根据任务确定结构角以实现对任务工作空间的完全包络。对任务轨迹的包络原则可适应复杂轨迹,具有一定的多任务普适性。 表1 结构角计算结果Table 1 Calculation results of structure angle (°) 图10 任务轨迹示意图Fig.10 Diagram of task trajectory 图11 任务工作空间示意图Fig.11 Diagram of desired workspace 下面针对此结构角下的构型进行任务轨迹仿真。设动平台中心点分别在时间t1,t2,t3时经过标定点T1,T2和T3。am(tn),vm(tn),sm(tn)分别为动平台中心点在时间tn时的加速度、速度、位移。故当动平台经过3 个标定点时,n=1,2,3;m=1z,2z,1′,2′。S1与S2分别经历加速与减速过程,结合运动稳定性考虑,可将加速度变化方程设为时间t的一次函数,则各运动参数方程形式可由式(13)得到,其中k1b(b=1,2,3,4,5)为时间t的系数。对3个标定点在S1与S2行程的运动参数关系式相互联立,可解出S1与S2的解析表达式。图12所示为动平台在执行任务轨迹时,xyz这3个方向上的位移变化曲线。 图12 动平台位移变化曲线Fig.12 Change curves of moving platform′s motion 将以上运动参数代入机构仿真模型,给定动平台中心点运动参数,完成抓取放置动作轨迹,输出机构驱动支链的长度变化曲线,如图13所示。从图12和13 可看出:当机构执行任务所需轨迹时,动平台与运动支链的运动曲线均无突变尖点,任务过程中对机构整体无冲击,证明该轨迹规划和机构结构设计是合理的,且机构的参数确定方法可适应相关任务需求。 图13 驱动支链长度变化曲线Fig.13 Change curves of motion branches length 1)提出了一种可用于箱体分拣的新型三自由度冗余驱动并联机构。通过中心转动副的加入实现了其工作空间的可变性,并确定了其动平台的运动性质。 2)通过含位置解、雅克比、奇异性在内的运动学分析,以及包括工作空间、灵巧度、刚度的性能分析,证明了该新型变工作空间并联机构具有多重任务适应性。 3)提出了具有任务适应性、基于运动学解算的机构参数确定方法。通过以工业生产线箱体分拣为背景的任务轨迹规划仿真,验证了机构设计的合理性及方法的普适性。4 应用分析
4.1 结构角确定方法

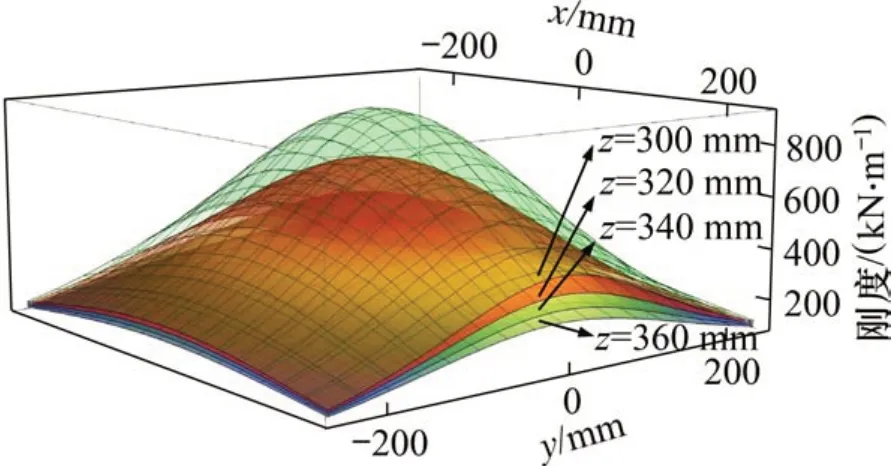
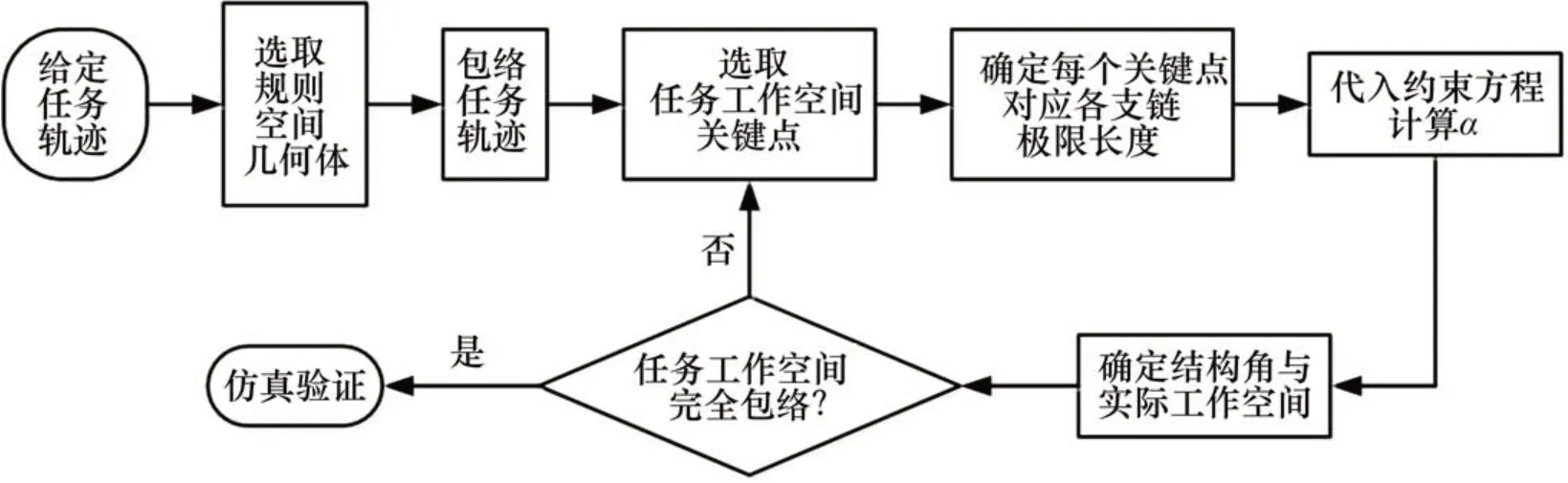

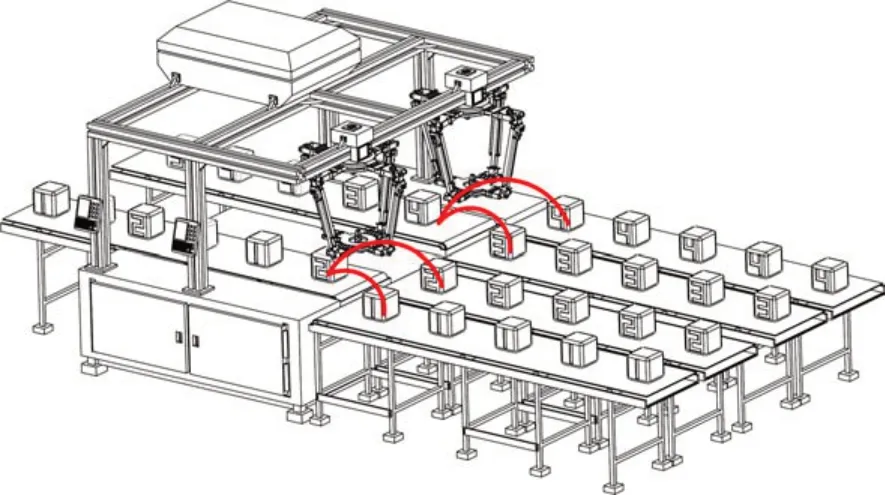
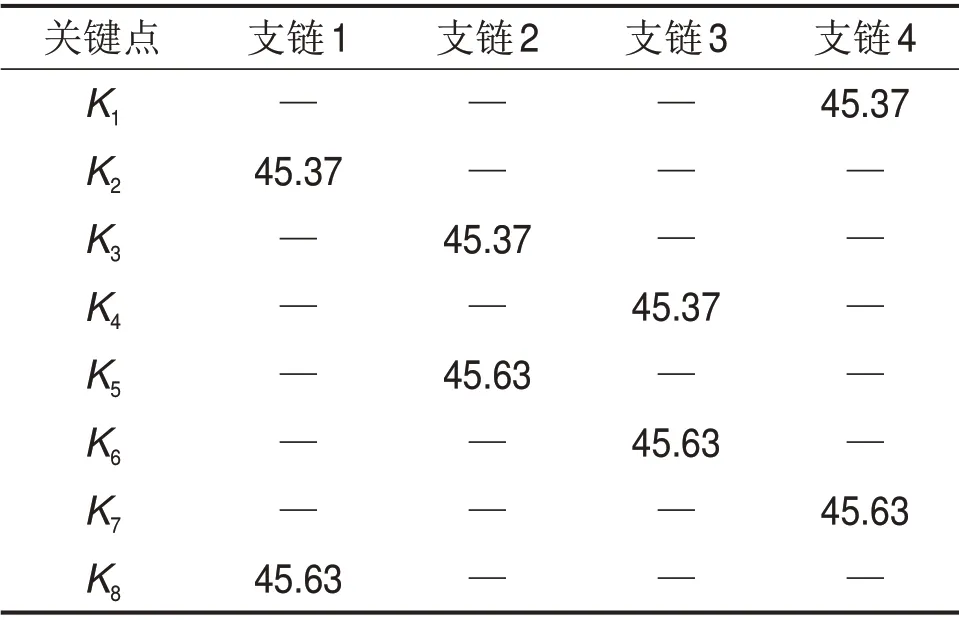
4.2 任务轨迹规划仿真


5 结论

