含支链闭环的结构冗余平面并联机构静力学分析
(北京交通大学机械与电子控制工程学院,北京,100044)
平面三自由度并联机构在工业机加工[1]、抓取搬运[2]、平面绘图及3C 产品包装等领域具有潜在应用价值,相对于空间并联机构,其结构简单,众多学者对平面并联机构的各种性能如工作空间[3]、运动奇异[4]、路径规划[5]、精度分析[6]、运动控制[7]、性能分析[8]、柔性纳米机构[9]、伪刚体分析[10]等进行了研究,为平面并联机构的应用奠定了基础。为了更好地提升并联机构的工作性能,众多学者考虑将冗余概念引入并联机构分析中。常见的冗余方法有驱动冗余和结构冗余等[11]。驱动冗余并联机构的驱动数目大于机构的自由度数目,而结构冗余并联机构的自由度数目等于机构的驱动数目,并大于动平台的输出自由度。结构冗余并联机构可以兼顾冗余的优点并克服驱动冗余引入的精准运动协调问题,尤其是能提升故障发生后机器人的容错能力而受到了广泛关注。GOSSELIN等[12]针对一种平面并联机构,研究了通过添加冗余结构进行机构的奇异规避方法,并指出结构冗余并联机构是并联机构新构型研究的出发点[12]。KANG等[13]对现有的平面3-RRR并联机构进行了冗余化处理,发现可以利用冗余结构避免第二类奇异。结构冗余除了可以扩展机构工作空间、规避奇异等外,还能提升机构静力学性能。机构静力学分析是进行运动分析及动力学分析的基础,搭建正确的静力学模型有助于了解机构在受外载荷时驱动关节的驱动力/力矩,为机构实物化结构尺寸的确定、优化及驱动电机选型提供了依据。众多学者利用不同方法如拆杆法[14]、杆件矢量法[15]、螺旋理论[16]、虚位移原理[17]等对并联机构的静力学进行了研究,其中虚功原理应用较广泛[18-24]。在平面并联机构的静力学研究方面,MOOSAVIAN 等[25]提出一种改进静态特性的变几何桁架机器人的研制方法,将其应用于欠驱动VGTM 模块设计,并讨论了一类新型可重构并联机器人的模块化设计方法,提升了机构静力学特性和机构的可靠性并改善了其静力学性能,可应用于机翼变形领域的性能改进[26]。WEN 等[27]针对三自由度平面并联机构的力控制,提出了一种刚度综合策略,有助于提高机构静力学性能。KOCK等[28]对一款平面2自由度驱动冗余并联机构进行了分析,发现引入冗余可以提高机构力传递性能及刚度。LIAN 等[29-33]借助有限元及螺旋理论对并联机构的静力学及刚度等问题进行了研究,并提出了指导并联机构最大限度减少振动和变形的优化设计方法,通过有限元模拟结果和实验对比分析结果进行了验证,完善了并联机构静力学分析方法。学者们还对结构冗余对平面并联机构静力学性能的改善进行了研究,如:BOUDREAU 等[34]提出了一款结构冗余平面并联机构,并将其与传统非冗余3-RRR 平面并联机构进行对比,发现结构冗余设计提升了机构的受力性能,提高了机构循迹能力;WEIHMANN等[35]提出了一种评估结构冗余平面并联机构受力能力的方法,并在给出的数值对比实验中,证实结构冗余平面机构的动平台所能承受的最大负载相比非冗余机构提高了25%;BI 等[36]提出了一种可重构的结构冗余平面并联机构,通过结构冗余调节实现了对PKM 的工作空间和整体刚度分布的调整,增强了机构对任务变量的适应性,此外,还提出了4种调整方案,以保证机构适用于高刚度和高负荷需求,从而改进并联机构静力学性能。本文作者对一款具有支链闭环的平面3-DOF 结构冗余并联机构[37](parallel mechanism with kinematic redundancy, PM-KR)进行其运动学及静力学分析。该机构在保留传统并联机构优点的前提下,可借助结构冗余支链的调节实现机构工作空间的扩展,为机构规避奇异提供可能,并有助于机构静力学性能提升。由于本平面结构冗余并联机构具有闭环特征,所以,进行静力学分析时,采用拆杆法将导致机构关系不明确,而采用矢量法时将引入多个中间变量;采用螺旋理论法则需要进行多次支链等效运动变换。为研究机构在受外载荷时驱动关节的驱动力/力矩,这里忽略被动关节受力及中间变量影响,采用具有闭环特征并联机构分析的虚功原理,建立该机构的静力学模型。本文首先对该机构的组成及运动学反解进行分析,借助虚功原理及雅克比矩阵,搭建动平台在受变载荷或变位置任务时的驱动关节静力学模型。其次,为验证模型正确性,对机构动平台位置固定受变载荷和位置变动受恒定载荷进行理论-仿真对比试验。最后,借助仿真软件与同特征尺寸下的3-RRR 平面并联机构进行同约束条件下的对比实验,通过仿真结果证实引入结构冗余有助于并联机构静力学性能提升。
1 运动学分析
1.1 PM-KR的设计由来及结构组成
传统3-RRR 平面并联机构在机构结构尺寸确定后,工作空间及其奇异将随之确定。若规划的路径因奇异存在被割裂在工作空间不同区域,末端执行器将难以完成任务。为解决该问题,通常有2 种改进方法:1)精简机构的杆件数量,如将3-RRR并联机构的动平台简化为1个两端为旋转副的杆件[38],此时,简化的3-RRR并联机构位姿具有解耦性[39],且可通过2个解耦的支链实现无奇异工作空间的设计[40];2)对3-RRR 机构进行结构冗余化处理,如将其中1条RRR支链由1条PRRRRP闭环支链取代,此时整机自由度变为4,大于动平台的相对自由度(RDOF)[37]3。将结构冗余化设计的3-RRR 并联机构称为平面结构冗余并联机构,由于其自由度大于完成操作任务所必需的最小自由度,因此,可以对引起机构自由度降低的故障如关节锁定故障等[41]进行容错。PM-KR 实物样机和PMKR CAD 模型分别如图1和图2所示。本机构通过2 个旋转电机和直线模组驱动(主要由直线滑台和对应的步进电机组成),协调配合动作实现动平台在x-y平面内移动和转动。
图2中各个零件沿z轴方向分层安放以避免各杆件相互干涉,为机构性能及结构冗余支链的调节提供了空间。
PM-KR 机构各部分参数符号的规定如图3所示,各部分结构参数如表1所示。定坐标系(O-xyz)与基座固连于点O,规定z轴垂直纸面向上,x轴穿过点A3和A4,y轴通过右手法则确定。动坐标系(p-uvw)与动平台固连于动平台几何中心点p,w轴垂直纸面向上,u轴平行于动平台边C2C3,v轴通过右手法则确定。
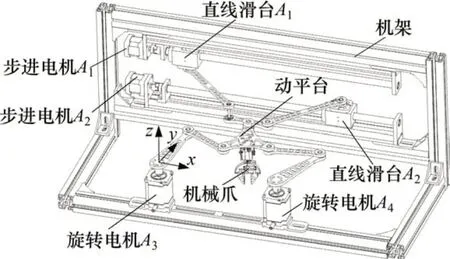
图2 PM-KR CAD模型Fig.2 CAD model of PM-KR
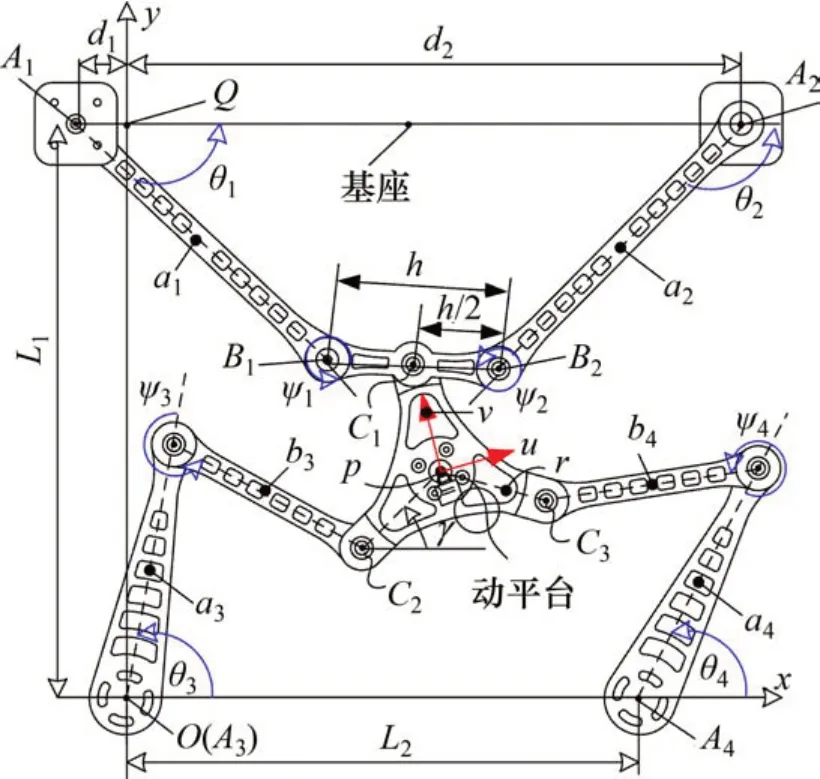
图3 PM-KR参数符号图Fig.3 Diagram of parameter symbols of PM-KR
该机构由动平台、基座、2条开环支链(支链3(A3B3C2)和支链4(A4B4C3))、1条闭环支链(QA1B1B2A2Q)组成,其中闭环支链又由2 条开环支链(支链1(A1B1C1)和支链2(A2B2C1))组成。2 条开环支链一端分别与正三角形动平台顶点C2和C3相连,另一端分别与固定在基座的旋转驱动相连于A3和A4。闭环支链与动平台连接于点C1。点C1是杆B1B2的中心,杆B1B2两端点分别通过杆A1B1与A2B2与移动驱动A1和A2相连接,由此根据该机构结构组成特点,将该机构命名为2-RRR-(P4RP)并联机构。为统一表述,这里将PM-KR 特指本文研究的平面机构冗余并联机构。
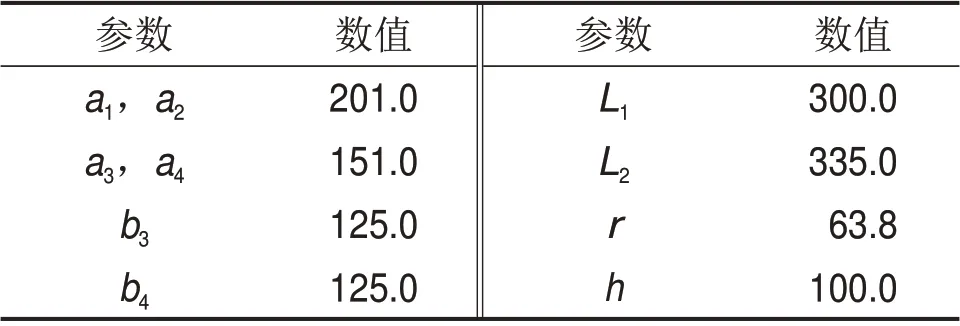
表1 PM-KR结构参数Table 1 The structural parameters of PM-KR mm
1.2 PM-KR的运动反解分析
当给定动平台位置和姿态参数xp,yp和γ后,需要求解的机构运动学反解参数为d1,d2和θ4。由于机构自由度数目大于动平台自由度数目,此时,运动学反解有无穷多个。为了得到唯一运动学反解,首先给定1 个驱动参数d1。动平台3 个顶点Ci(i=1,2,3)在动坐标系p-uvw下记为pCi(i=1,2,3),pCi动坐标系p-uvw下的三维坐标写为矩阵形式为
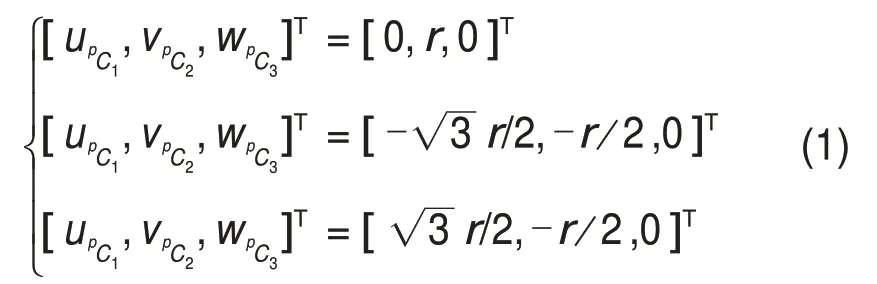
通过坐标变换公式(2),可以得到动平台3个顶点Ci(i=1,2,3),在定坐标O-xyz下的三维坐标(xCi,yCi,zCi)写为矩阵的形式为:
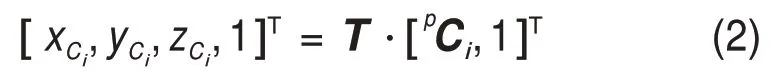
式中:T为动平台位姿的齐次变换矩阵,
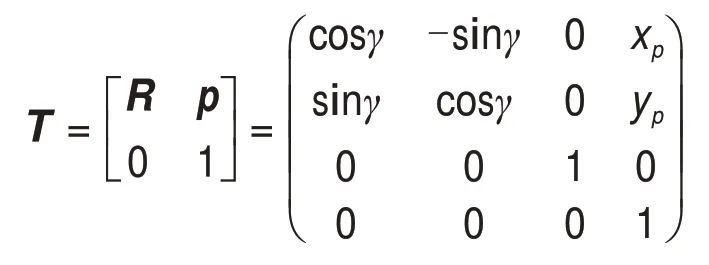
求解式(2)可得动平台3 个顶点Ci(i=1,2,3)在定坐标系下的三维坐标的具体矩阵形式为:
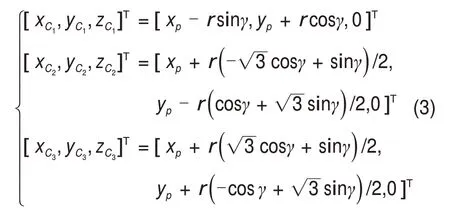
借助封闭矢量环路法,可依次建立2条开环及1条闭环支链与动平台、基座三者之间的关系式:

由式(4)和已知的动平台参数[xp yp γ],借助杆长约束等条件可以得到该机构的反解表达式:
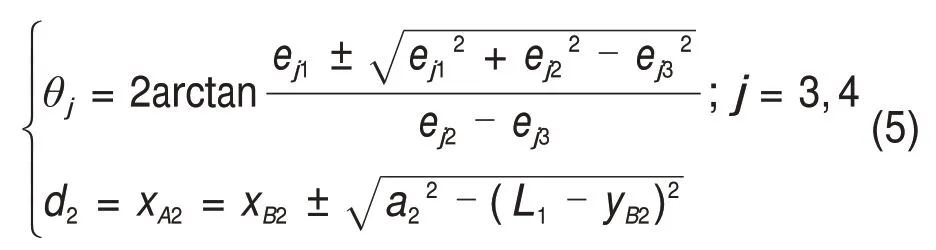
由式(5)可知,当动平台位置给定后,θ3,θ4和d2通常具有2个解。尤其需要注意的是,在求解变量d2时,牵涉1个中间变量θ1,这个变量自身也具有2个解且与d2紧密联系,它们之间的关系为
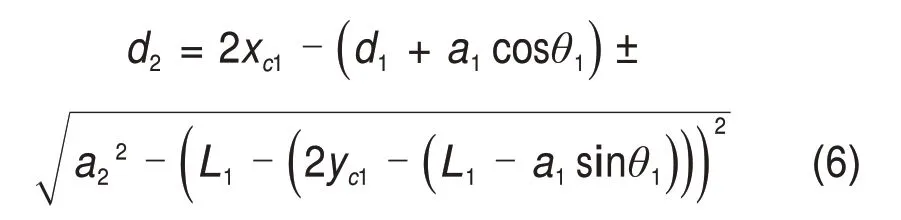
因此,参数d2事实上具有4 种可能解,这样,整机存在16 组反解。反解及中间变量θ1的具体推导过程见参考文献[37]。
为了确定运动学反解的解析表达式与机构运动位形(具有某种初始安装位形)之间的对应关系,需要对16 组反解进行选择。本文在Solidworks 中建立如图2所示的机构模型,并将测得的动平台位姿参数依次代入16组运动学反解中,将式(5)和(6)计算的运动学反解与Solidworks仿真模型中测量的对应反解参数进行对比,若所有理论值与仿真测量值均相同且代入不同的动平台位姿参数仍然相等,则可以从16 组反解中选择出符合图2所示初始安装位形下的运动学反解表达式,此时,式(5)及(6)中的“±”将具有确定性:θ3的反解表达式取“+”,θ4的反解表达式取“-”,θ1的反解表达式取“+”,d2的反解表达式取“+”。
2 PM-KR静力学理论模型搭建
静力学分析在研究并联机构力学性能方面尤为重要。虚功原理在并联机构的静力学分析中仅考虑动平台在受外加载荷时驱动关节的驱动力/力矩的变化,而忽略被动关节的作用力或力矩,与其他方法相比更加简洁,可操作性更强。因此,本文采用该方法进行静力学模型搭建。
2.1 机构静力学模型建立
为方便研究,视机构的各主、被动关节均无摩擦且被动关节处亦无虚功,并且忽略重力对平面并联机构静力学模型搭建的影响。
首先将作用在动平台上的外加载荷记为F=[fDT,τDT]T,其中,fD与τD分别为施加在动平台上的力与力矩。将作用在驱动关节处的力或力矩统一记为τ=[τ1,τ2,…,τn]T,将与驱动关节相关的虚位移变化记为δQ=[δq1,δq2,…,δqn]T,相应地,将与动平台相关的虚位移记为δX=[δx,δy,…,δγ]T。由以上要素结合虚功原理可以得到作用于所有驱动关节的驱动力/力矩的虚功:
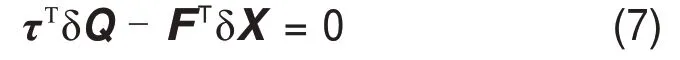
式(7)中驱动与动平台虚位移关系为[42]

式中:J为机构的雅克比矩阵,J=JQ-1JX;JQ为机构正雅克比矩阵;JX为机构逆雅克比矩阵[42]。
将式(8)代入式(7),为满足任意虚位移δX的变化,得到主驱动与动平台间的静力学关系式:

由此得到动平台输出力与驱动关节的驱动力/力矩间的表达关系式。从式(9)可知,动平台与驱动关节的驱动力/力矩间的力传递关系与机构的位姿联系密切。
由于本机构含结构冗余闭环支链,采用冗余参数d1对机构静力学进行分析时,其所在的移动关节即直线滑台A1实际也可用于静力学分析。为此,首先分析冗余参数d1给定时机构处于非冗余状态下的静力学模型,得到此时机构其他驱动关节的驱动力/力矩。其次,将与结构冗余参数d1处于同一闭环的变量d2相结合,借助虚功原理对二者所在的闭环支链进行二次静力学建模。并将2.2节得到的直线滑台A2的驱动力作为已知量,在闭环支链中结构冗余直线滑台A1与直线滑台A2静力学关系建立后,将直线滑台A2驱动力代入,最终得到全部驱动关节的驱动力/力矩。这里需强调的是,直线滑台A1与A2的驱动力特指沿两者几何中心连线方向作用的力,该力最终由所在直线模组的步进电机A1或A2提供,为表述方便,以下将直线滑台A1与A2的驱动力统称为驱动关节A1与A2的驱动力或驱动A1和A2的驱动力;直线滑台A1与直线滑台A2统称为驱动A1与驱动A2;步进电机A3与步进电机A4的驱动力矩统称为驱动关节A3与A4的驱动力矩或驱动A3与A4的驱动力矩;步进电机A3与步进电机A4统称为驱动关节A3与A4。
2.2 冗余参数给定下的静力学模型建立
本节分析冗余参数d1给定情况下非冗余平面并联机构的静力学模型,当结构冗余参数d1给定后,得到的机构雅可比矩阵为方阵。
选取动平台广义坐标为X1=[xp,yp,γ]T,驱动关节广义坐标为Q1=[θ3,θ4,d2]T,同理动平台的虚位移记为δX1=[δxp,δyp,δγ]T,驱动关节虚位移记为δQ1=[δθ3,δθ4,δd2]T,动平台上的外加载荷记为F1=[fxp,fyp,τγ]T,将作用在驱动关节处的力或力矩记为τ1=[τθ3,τθ4,fd2]T。借助式(9)得到给定结构冗余参数d1时的PM-KR 任意位形下的驱动与动平台静力学传递关系:

J1=JQ1-1JX1,为给定结构冗余支链位置下的PM-KR整机雅克比矩阵,其计算过程如下。
1)建立基于封闭环路矢量法的动平台与主驱动关节间的隐函数:

2)对隐函数两侧分别对时间求微分得到雅克比矩阵所需元素。
由式(11),支链3的隐函数可以改写为
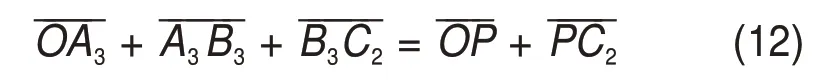
式(12)在O-xyz坐标系下沿x和y轴的投影分别为:
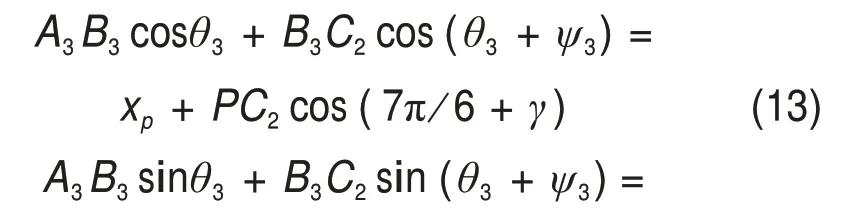
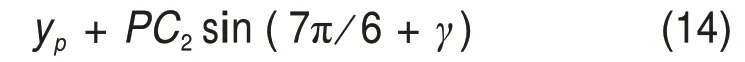
联立式(13)和(14),消去中间变量ψ3,得

式中:M3=A3B3cosθ3-xp-PC2cos(7π 6+γ);N3=A3B3sinθ3-yp-PC2sin(7π 6+γ)。
将式(15)两边同时对时间求微分,可得雅克比矩阵第1行元素。
同理,采用式(12)~(15)对支链4和2进行计算,可得式(17)和(18),对式(17)和(18)两侧分别对时间求微分得雅可比矩阵第2和第3行元素。
对于支链4,其环路方程为

由于支链4 的环路方程(16)在O-xyz坐标系下沿x、y轴的投影也存在中间变量ψ4,为消去ψ4,也需要联立式(16)在O-xyz坐标系下沿x和y轴的投影表达式,得
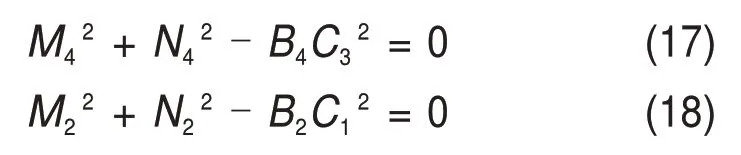
式中:M4=L2+A4B4cosθ4-xp-PC3cos(γ-π 6);N4=A4B4sinθ4-yp-PC3sin(γ-π 6);M2=d2+A2B2cosθ2-xp-PC1cos(γ+π 2);N2=L1+A2B2sinθ2-yp-PC1sin(γ+π 2)。
同理,对于支链2,其环路方程及简化形式为
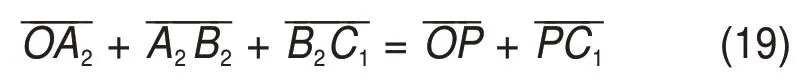
由于支链2 的环路方程(19)在O-xyz坐标系下沿x、y轴的投影也存在中间变量ψ2,为消去ψ2,也需要联立式(19)在O-xyz坐标系下沿x和y轴的投影表达式,得式(18)。
将式(15),(17)和(18)分别对时间求微分,并改写为矩阵形式,得

式中:JQ1为R3×3的方阵;JX1为R3×3的对角矩阵;为驱动速度矢量;为动平台速度矢量;和为驱动关节的角速度;为驱动关节的速度;和为动平台移动速度;为动平台转动的角速度。
2.3 结构冗余并联机构的静力学模型
由式(10)仅能推导出机构3 个驱动关节的驱动力/力矩与动平台外载荷之间的静力传递关系,但结构冗余支链的驱动A1也参与了机构静力学分析,由此也需推导出动平台外载荷与结构冗余支链驱动A1的静力学关系表达式。
当给定动平台外载荷且动平台位姿确定时,可以计算出驱动关节A2的驱动力。结构冗余驱动A1与驱动A2同时位于闭环支链中,如图4所示,此时,动平台视为与地面固定。当闭环支链在结构冗余参数d1给定时,自由度为0。但从虚功原理的角度分析其静力学特性,闭环支链中A1有运动的趋势。
将闭环支链的结构冗余参数d1的微小变化趋势即虚位移δd1视为输入即该环路的动平台参数,相应的视驱动A2参数的微小变化趋势即虚位移δd2看作输出即该环路的驱动参数。该环路动平台上的外加载荷记为fd2,将作用在闭环支链驱动关节处的驱动力记为fd1。其闭环支链参数及静力分析符号如图4所示,图4中的锁表示动平台位置固定,虚线表示该杆件不参与分析。

图4 闭环支链参数及静力分析符号Fig.4 Diagram of closed loop chain parameters and statics analysis symbols
由式(9)得到给定结构冗余支链位置下的PMKR任意位形的驱动关节的驱动力与动平台静力学传递关系式为

此时,fd2与式(10)中的fd2相同。δJ2=δJq2-1δJX2,δJ2为给定动平台位姿下的闭环支链速度雅克比关系式。其中:δJq2为闭环的速度正雅克比关系式;δJX2为闭环的速度逆雅克比关系式。计算过程如下。
1)针对闭环支链,建立基于封闭环路矢量法的动平台与驱动关节间隐函数:
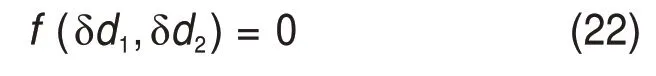
2)对隐函数两侧分别对时间求微分,得到雅克比关系所需元素。
将闭环支链的隐函数改写为封闭矢量环路形式:
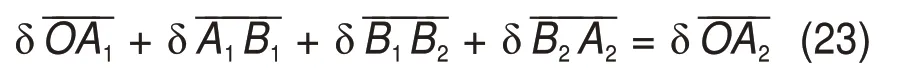
式(23)在O-xyz坐标系下沿x轴的投影表达式为
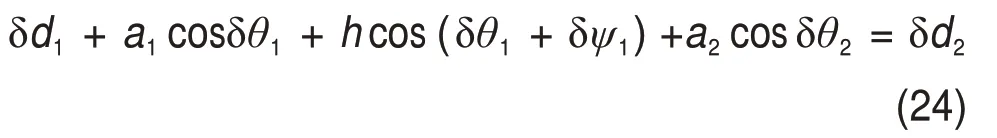
式中:δθ1,δθ2和δψ1分别为中间变量θ1,θ2和ψ1的微小变化趋势即虚位移;δxp,δyp和δγ分别为动平台位姿变量xp,yp和γ的微小变化趋势即虚位移;为为虚位移δd2的移动速度;为为虚位移δd1的移动速度。
通过第1 节分析可知δθ1,δθ2和δψ1这些中间变量均可被替换为含有δxp,δyp,δγ,δd1和δd2的表达式,在研究闭环支链时,由于整机动平台的位姿是确定的,因此,式(24)中δxp,δyp和δγ为常数,式(24)变为仅含有δd1和δd2这2个独立参量的表达式。
对式(24)两侧分别对时间求微分,改写为速度雅可比关系形式,可表示为

结合2.2 与2.3 节的分析,当整机动平台位姿及外加载荷给定时,借助式(10),可得3 个驱动力或力矩:

将式(26)求得的驱动力fd2代入式(21),便可求得结构冗余支链驱动A1的驱动力fd1。至此,建立了该机构给定动平台外载荷时,求解驱动驱动力/力矩的理论模型,其具体求解流程如图5所示。
3 理论-仿真数值对比实验
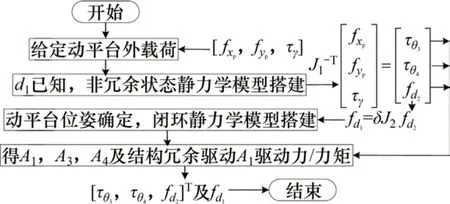
图5 PM-KR静力学分析流程Fig.5 Flow chart of statics analysis of PM-KR
为验证第2节提出的机构静力学理论模型的正确性,设定了2个常见的静力数值工况实验:1)机构动平台沿圆轨迹随圆心角变化而变化位置,执行对动平台施加恒定外载荷的任务;2)动平台停留在圆轨迹某一圆心角对应位置,执行在动平台上施加变外载荷的任务。为了简化分析,假定动平台姿态角γ=0°,这里选取结构冗余参数d1=300 mm 及d1=340 mm 共2 种状态。在机构执行上述2 项实验任务后,考察机构驱动力/力矩的数值变化及曲线趋势,以验证结构冗余的引入对并联机构的静力学性能的调节作用。
3.1 恒定外载荷下的静力数值分析
设定动平台圆轨迹方程为
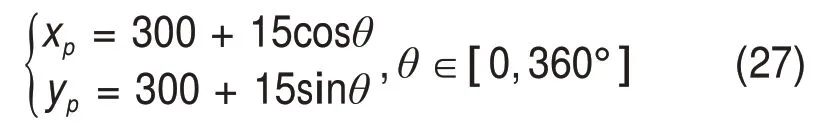
给定动平台外载荷为:fxp=5N;fyp=5N;τγ=4 N·mm。
动平台圆轨迹随圆心角变化而变化,由此得到圆轨迹不同位置下的3个驱动及结构冗余支链所在驱动的驱动力或力矩。同时,将与理论模型所采用的同尺寸的机构Solidworks 模型导入Adams软件进行静力学仿真。理论模型所得结果与Adams 计算所得结果见图6和图7。图6和图7中,A1和A2的理论结果或仿真结果分别指驱动A1和A2的驱动力理论结果或仿真结果;A3和A4的理论结果或仿真结果分别指驱动A3和A4的驱动力矩理论结果或仿真结果。
从图6和图7可以看出:3 个驱动及结构冗余支链驱动的驱动力/力矩理论结果与仿真结果变化趋势一致。
对比图6和图7可以发现:结构冗余参数从d1=300 mm(I 状态)调节为d1=340 mm(II 状态)后,执行相同任务的机构静力学性能发生改变,这里选取调整前后对应驱动理论值进行对比:驱动A3和A4的驱动力矩曲线变化趋势相似,驱动A3的驱动力矩曲线整体上II 状态时的值比I 状态时的值小,在圆心角为250°时,驱动A3的驱动力矩差值最大为254.583 N·mm;驱动A4的驱动力矩曲线的驱动力矩整体数值在II状态时比I状态小,在圆心角为240°时,驱动A4的驱动力矩最大差值为263.853 N·mm。同时,驱动A1和A2的驱动力曲线趋势前后差距大,驱动A1的驱动力曲线II 状态时的整体数值比I 状态时的小;在圆心角为230°时,驱动A1的驱动力最大差值为0.855 N;驱动A2的驱动力曲线的整体数值在II状态时比I状态大,在圆心角为230°时,驱动A2的驱动力差值也最大,为0.829 N。由此可见,结构冗余的引入对并联机构的静力学性能有调节作用。
为进一步量化考察理论模型的正确性,选取d1=300 mm 时的理论值与仿真值相对误差进行对比,如图8和图9所示。从图8和图9可以看出:理论模型最大相对误差为0.774%,进一步说明了该理论模型的正确性。
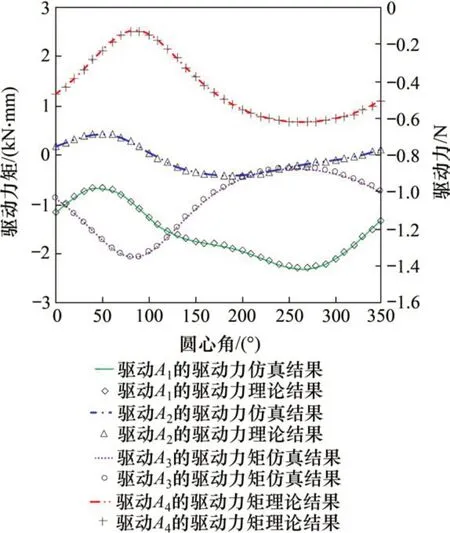
图6 变动平台位置且载荷恒定时驱动力/力矩的理论结果-仿真结果对比(d1=300 mm)Fig.6 Comparison of theoretical results and simulation results of driving force/torque when platform position is changed and load is constant(d1=300 mm)
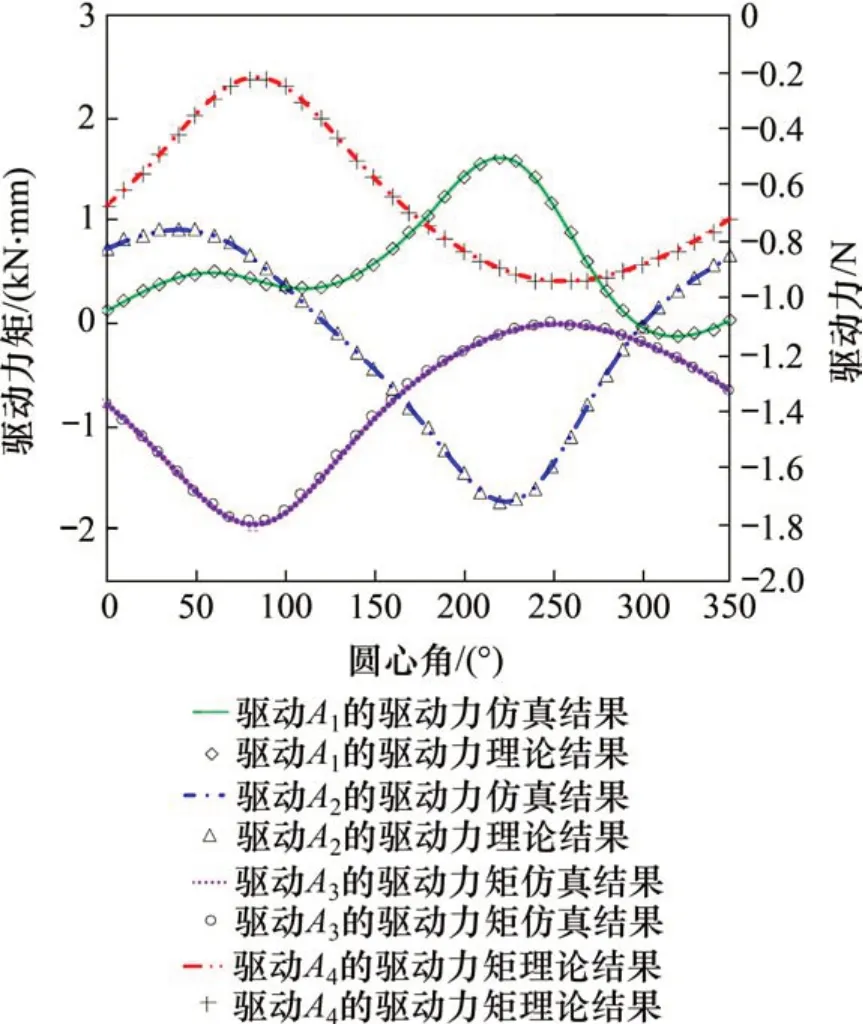
图7 变动平台位置且载荷恒定时驱动力/力矩理论结果-仿真结果对比(d1=340 mm)Fig.7 Comparison of theoretical results and simulation results of driving force/torque when platform position is changed and load is constant(d1=340 mm)
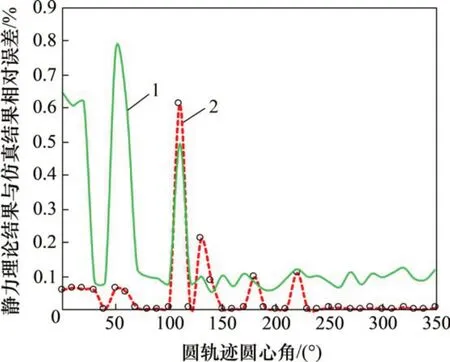
图8 变动平台位置的驱动力理论结果与仿真结果相对误差Fig.8 Relative error of theoretical results and simulation results of driving force/torque when platform position is changed
3.2 变外载荷下的静力数值分析
不失一般性,选取动平台处于圆心角θ为180°时的位置,姿态角γ=0°。将该情况下PM-KR 的Soliworks 模型导入Adams 软件中,施加随时间变化的外载荷:
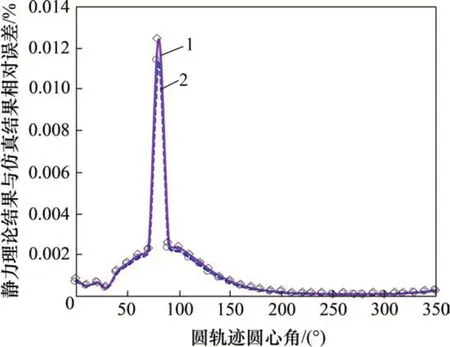
图9 变动平台位置的驱动力矩理论结果-仿真结果相对误差Fig.9 Relative error of theoretical results and simulation results of driving torque when platform position is changed

同理,选取结构冗余参数d1=300 mm 及d1=340 mm这2种状态进行分析,得到执行如式(28)所示任务时各驱动关节理论与仿真的驱动力/力矩,如图10至图13所示。从图10至图13可知:在数值变化趋势及数值这2个方面,理论模型计算值均与仿真值相同。对d1=300 mm时的理论结果与仿真结果相对误差进行对比,得到图10的驱动A1与A2的力矩理论相对仿真误差最大为0.1356%,图12的驱动A3与A4的力矩理论相对仿真误差最大为0.003%,由此证明该理论模型在动平台受变外载荷时也能正确求解。
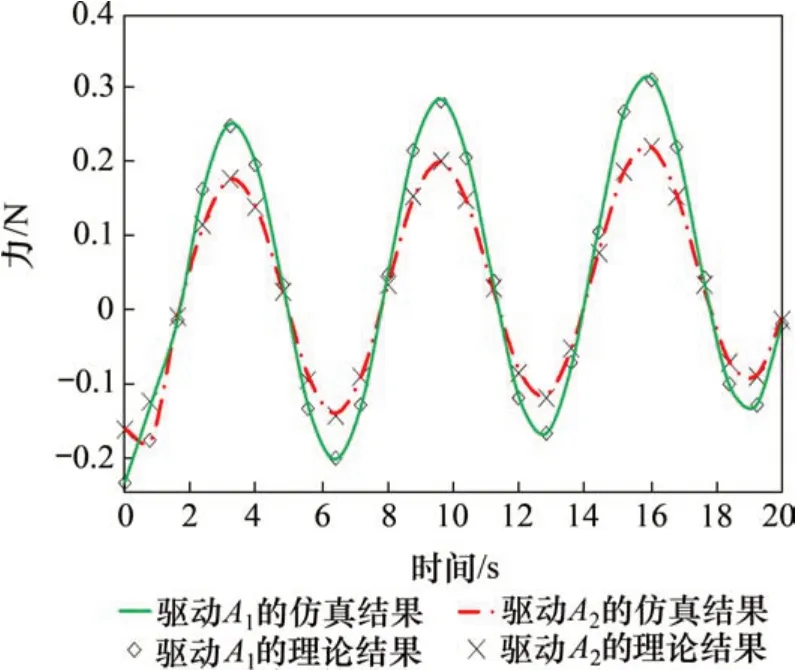
图10 驱动A2力与驱动A1力理论结果与仿真结果对比(d1=300 mm)Fig.10 Comparison of theoretical results and simulation results of driving A2 and driving A1(d1=300 mm)
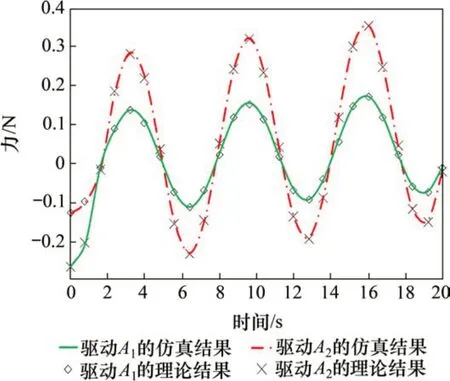
图11 驱动A2力与驱动A1力理论结果与仿真结果对比(d1=340 mm)Fig.11 Comparison of theoretical results and simulation results of driving A2 and driving A1(d1=340 mm)

图12 驱动A3力矩与A4力矩理论结果与仿真结果对比(d1=300 mm)Fig.12 Comparison of theoretical results and simulation results of driving A3 and driving A4(d1=300 mm)
下面分析结构冗余参数d1对并联机构静力学性能的影响。对比图10和图11中对应驱动力及变化趋势可以发现:结构冗余参数从d1=300 mm(I状态)调节为d1=340 mm(II 状态)后,执行相同任务的机构静力学性能发生改变。这里选取调整前后对应驱动理论值进行对比:驱动A1和A2的驱动力曲线趋势前后差距大,驱动A1的驱动力曲线在II 状态时的整体数值绝对值比I 状态时的小,在16 s,驱动A1的驱动力差值最大为0.142 6 N;驱动A2的驱动力曲线在II状态时的整体数值绝对值比I状态时的大,在0 s 时,驱动A2的驱动力差值最大为0.529 33 N。
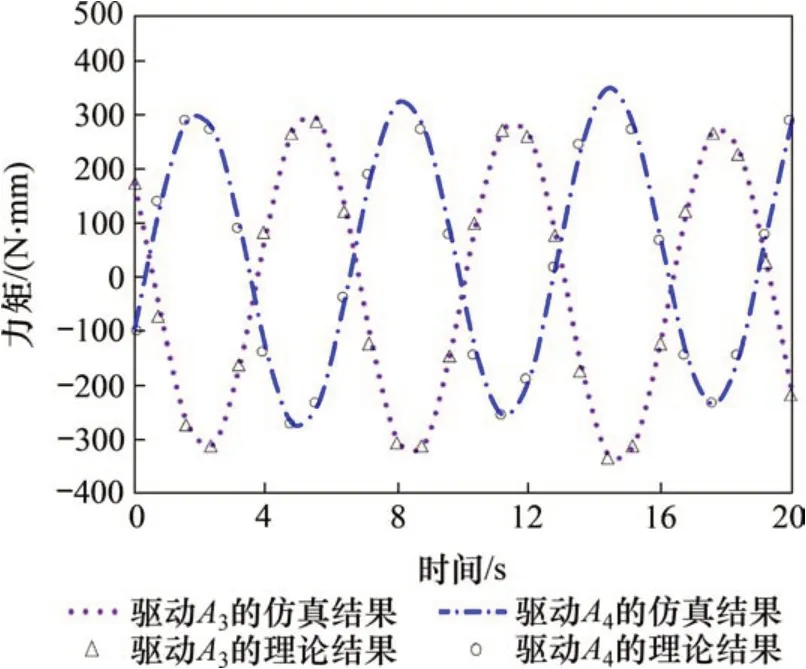
图13 驱动A3力矩与A4力矩理论结果与仿真结果对比(d1=340 mm)Fig.13 Comparison of theoretical results and simulation results of driving A3 and driving A4(d1=340 mm)
同时,对比图12和图13中的驱动力矩及变化趋势可以发现:驱动A3和A4的驱动力矩曲线变化趋势前后差距小;在16 s 时,驱动A3的驱动力矩差值最大为64.94 N·mm;同时,驱动A4的驱动力矩差值也最大,为90.287 N·mm。由此可见,结构冗余的引入对变载荷情况下并联机构的静力学性能也有调节作用。
4 PM-KR与3-RRR仿真对比实验
结构冗余的设计不仅有利于并联机构规避奇异,扩展工作空间,而且有益于其静力学性能的提升。
本机构的设计源于对传统平面3-RRR 并联机构的改进,因此,本文将对PM-KR 和3-RRR 平面并机构的静力学性能进行对比研究。为了简化研究,此处选取冗余参数d1=300 mm,3-RRR机构的结构尺寸选取与PM-KR 的一致,执行的任务也相同,其结构参数按图14所示进行规定,尺寸如表2所示。
3-RRR 的静力学理论模型已得到广泛研究[42]。PM-KR 的理论模型的正确性已得到证实,因此,为确保系统误差对对比结果不产生影响,依照对比试验条件一致原则,将Solidworks中建立的2款机构模型导入同一环境下的Adams 软件中,执行下列2项任务。

图14 3-RRR平面并联机构参数符号规定Fig.14 Diagram of parameter symbols specification of 3-RRR planar parallel mechanism
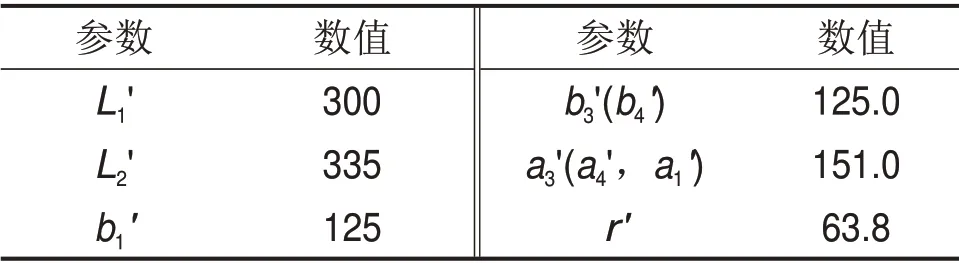
表2 3-RRR结构参数Table 2 Structural parameters of 3-RRR mm
4.1 动平台外载荷恒定,执行沿圆轨迹变位置任务
本节中动平台执行的圆轨迹方程如式(27)所示,作用在动平台上的外载荷为:fyp=5 N;fxp=5 N;τγ=4 N·mm。执行变轨迹任务后,得到了PMKR与3-RRR平面并联机构的驱动力矩变化图,如图15所示。2种平面并联机构驱动力矩的变化趋势近似但在数值上存在差异,其驱动力矩的峰值对比如表3所示。
从表3可知,在施加在动平台上的外载荷恒定的前提下,动平台位置沿圆轨迹变化时,PM-KR的A3驱动力矩相比于3-RRR 的A3'驱动力矩峰值下降28.5%;PM-KR 的A4驱动力矩相比于3-RRR 的A4'驱动力矩峰值下降25.3%,且在整个运行周期范围内,PM-KR 的A3与A4驱动力矩分别小于3-RRR的A3'与A4'驱动力矩。
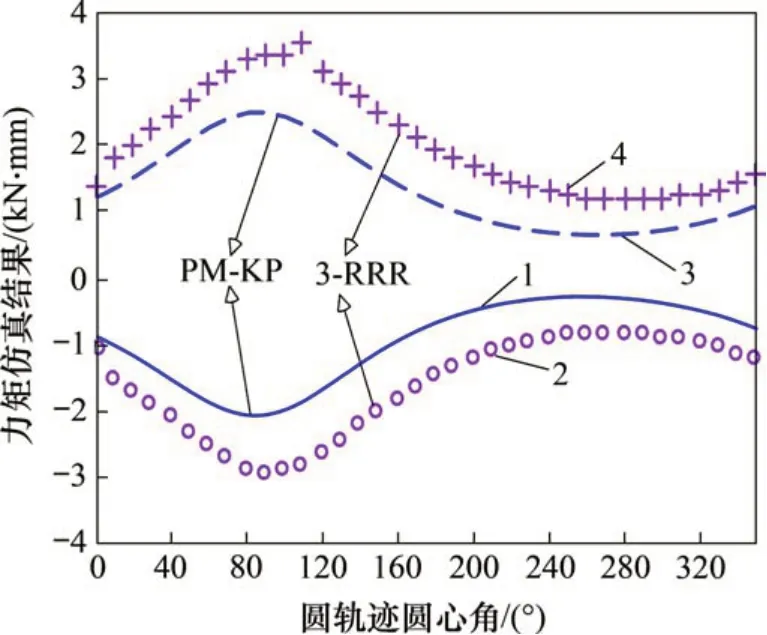
图15 变动平台位置且载荷恒定时驱动力矩仿真结果对比Fig.15 Comparison of simulation results of driving torque when platform position is changed and load is constant

表3 PM-KR与3-RRR平面并联机构驱动力矩峰值对比表(外载荷恒定的变轨迹任务)Table 3 Comparison table of driving moment peaks for PM-KR and 3-RRR planar parallel mechanism(variable trajectory task with constant external load)
由于PM-KR 的闭环支链包含2 个直线滑台A1和A2,而与之对应的3-RRR的支链1,A′1B′1C′1则含有1个转动驱动A1',因此,为比较两者对应的驱动力或力矩,需要统一量纲。从图2可知,直线滑台与杆件之间依靠轴承连接形成R 副,无减速装置,减速比为1;直线模组与基座固连水平放置,倾角为0°;直线模组采用滚珠螺杆进行传动,而直线模组的动力来源于与螺杆通过联轴器,无减速装置直接连接的步进电机,又由于直线滑台A1和A2所在的滑台受力形式(如图4所示)为沿两滑台连线的力,滑台无预负载,因此,可借助简化的滚珠螺杆直线模组电机选型(式(29))[43],将直线滑台A1和A2所受的力fd1和fd2转化为对应步进电机的扭矩τd1和τd2。这里需要强调的是,式(29)考虑了滑台及其负载质量,与平面静力学模型处于同一势能面,故可忽略重力带来的影响。
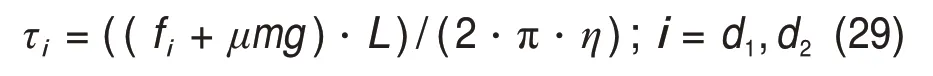
式中:η为传递效率,参考值为0.85~0.95,选取0.90;μ预压螺母的内部摩擦因数,有润滑时取0.1;m为滑台及负载质量,m=5 kg;g为重力加速度,g=9.8 m/s2;L为螺杆导程,L=10 mm。
为便于比较,将驱动A1、驱动A2借助式(29)换算得到的扭矩τd1和τd2按式(30)进行加和运算等效为驱动A1A2(力矩为τd1-d2),然后与3-RRR 的A1'驱动进行对比。
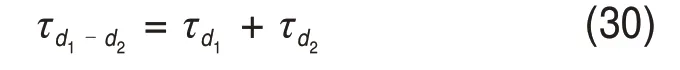
驱动A1A2与驱动A1'的驱动力矩对比如图16所示。从图16可见:在整个任务运行周期内,驱动A1'的驱动力矩绝对值变化范围为(170,330)N·mm,而驱动A1A2的驱动力矩变化范围为(13,14.6)N·mm,驱动A1'的力矩是驱动A1A2力矩的10 倍,因此,PM-KR 闭环支链的驱动静力远小于3-RRR 机构驱动A1'的驱动静力。
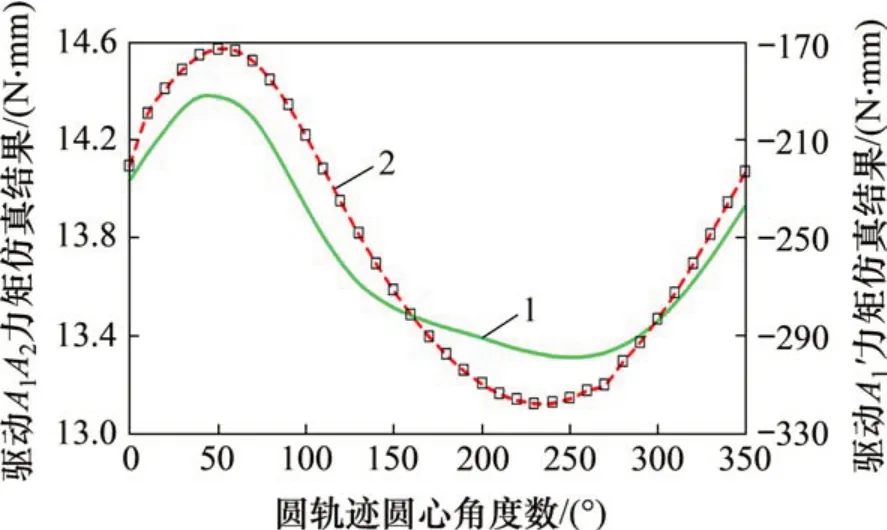
图16 变动平台位置且载荷恒定时驱动力矩仿真结果对比Fig.16 Comparison of simulation results of driving torque when platform position is changed and load is constant
对比图15和16可知:PM-KR各驱动输出力矩相比于3-RRR 各驱动力矩明显下降,证实在动平台外载荷恒定、执行沿圆轨迹变位置任务时,结构冗余的引入能有效改进机构驱动关节受力性能,从而改善整机静力学性能。
4.2 动平台位姿固定,执行外载荷变化任务
本节中施加给动平台外载荷形式、大小如式(31)所示,动平台位姿及其他参数设定与3.2 节中的相同。

执行变外载荷任务后,得到PM-KR 与3-RRR平面并联机构的驱动力矩变化图,如图17所示。2种平面并联机构驱动力矩的变化趋势近似但在数值上存在差异,其驱动力矩的峰值对比如表4所示。
从表4可以看出:在外加载荷变化而动平台位姿固定时,PM-KR 的A3驱动力矩相比于3-RRR 的A3'驱动力矩峰值下降54.6%;PM-KR 的A4驱动力矩相比于3-RRR的A4'驱动力矩峰值下降42.7%。
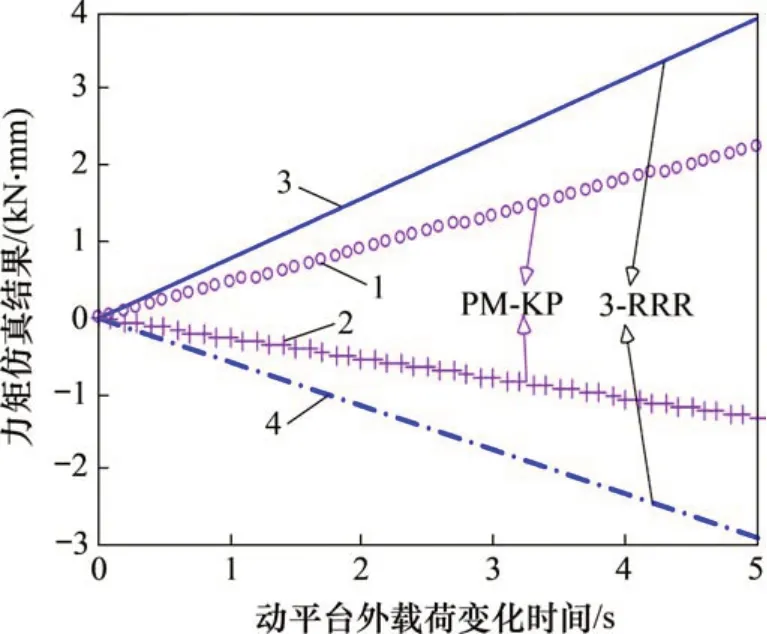
图17 位姿固定变载荷时驱动力矩仿真结果对比Fig.17 Comparison of simulation results of driving torque when platform load is changed and position is constant
采用4.1节中驱动A1和A2所受的力fd1和fd2转化为对应步进电机的扭矩τd1和τd2的方式,可得驱动A1A2与驱动A1'的驱动力矩变化图,如图18所示。从图18可见:在整个任务运行周期内,驱动A1'的驱动力矩的绝对值变化范围为(0,600) N·mm,而驱动A1A2的驱动力矩变化范围为(8,18)N·mm,可见尽管在任务开始时,驱动d1d2的驱动力矩比驱动A1'的大,但在1 s后,两者驱动力矩变化逐渐增大,驱动A1'的力矩是驱动A1A2的10倍不等,因此,PM-KR 闭环支链的驱动静力整体上小于3-RRR机构驱动A1'的驱动静力。

表4 PM-KR与3-RRR平面并联机构驱动力矩峰值对比(变外载荷的定位姿任务)Table 4 Comparison of driving moment peaks for PM-KR and 3-RRR planar parallel mechanism(positioning fixed task of variable external load)
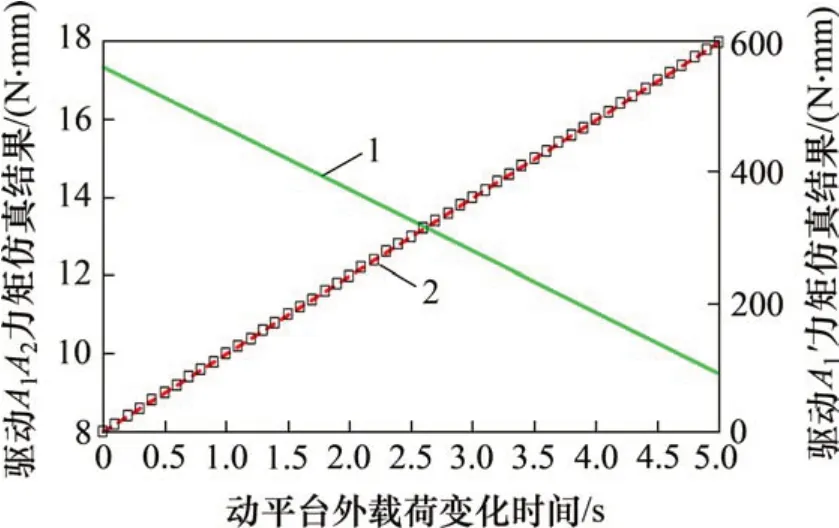
图18 位姿固定变载荷时驱动力矩仿真结果对比Fig.18 Comparison of simulation results of driving torque when platform load is changed and position is constant
对比图17和18可知:PM-KR各驱动输出力矩相比于3-RRR 各驱动力矩明显下降,证实在动平台位姿固定、执行外载荷变化任务时,结构冗余的引入也能有效改进机构驱动关节受力性能,从而改善整机静力学性能。
5 结论
1)建立了含支链闭环的结构冗余并联机构的静力学模型。基于变轨迹和变外载荷2种情况下的静力学理论与仿真对比分析,从数值及变化趋势2个维度验证了静力学理论模型的正确性。
2)通过执行变轨迹和变载荷任务,验证了结构冗余参数对机构驱动/驱动力的影响,为结构冗余并联机构的力学特性改进奠定了基础。
3)在执行相同变轨迹和变外载荷任务时,本文机构相比传统非冗余3-RRR 并联机构的驱动力矩在整个运行周期内明显下降,这有利于改进机构力传递特性,提升整机静力学性能。

