动量定理有效处理变量、瞬时及连续作用问题

湖北 王宝生

动量定理和动量守恒定律是物理学的重要规律，2017年高考《考试大纲》将选修3-5的内容调整为必考，在随后几年高考、大型联考等考试中动量定理和动量守恒定律就成了一个新热点，并且题型不再拘泥于过去传统的一维水平碰撞、反弹等经典题型，涌现出很多新题型。这其中一个很重要的原因就是动量定理涉及力，而整个高中知识点几乎都和力有关，这样结合后知识间衔接点就非常多，个人认为更多的新题型将大量涌现。

二轮复习要从基础知识出发，逐步深化和拓展应用能力。对于动量定理，可以在用动量定理处理变量、瞬时及连续作用问题上做文章。

一、处理变质量问题

对于研究对象为“变质量”的“连续”的流体(如水流、空气流等)问题，现以水流为例做探讨。这类问题一般要假设一段时间Δt内流出的水柱，其长度可表述为vΔt，水柱横截面积为S，就可得出水柱体积V=SvΔt，进而得到水柱质量Δm=ρV=ρSvΔt，再对质量为Δm的水柱应用动量定理求解。

【例1】(2016年全国卷Ⅰ)某游乐园入口旁有一喷泉，喷出的水柱将一质量为M的卡通玩具稳定地悬停在空中。为计算方便起见，假设水柱从横截面积为S的喷口持续以速度v0竖直向上喷出；玩具底部为平板(面积略大于S)；水柱冲击到玩具底板后，在竖直方向水的速度变为零，在水平方向朝四周均匀散开。忽略空气阻力，已知水的密度为ρ，重力加速度大小为g。求：

(1)喷泉单位时间内喷出的水的质量；

(2)玩具在空中悬停时，其底面相对于喷口的高度。

【例2】气垫导轨可有效减小摩擦力，如图1所示为气垫导轨示意图。每个滑块有两个侧面，侧视图为等边三角形，单个侧面对应气孔面积为S，假设气流(密度为ρ)从横截面积为S的喷口持续以速度v0喷出，并以v0垂直作用侧面上后在垂直侧面方向上速度减为零，滑块悬浮在导轨上方。试求单个滑块的质量m。

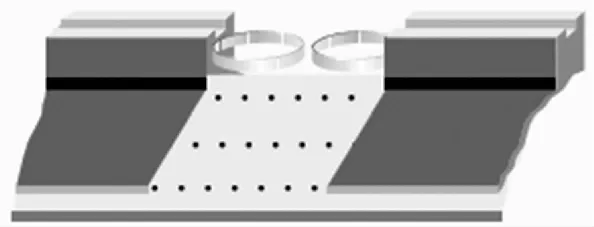
图1

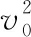
【总结】两个例题中均采用先假设出一段时间，先求出单位时间“流出”的质量。例1是结合机械能守恒求出水流与玩具作用前的速度，例2是直接给出气流与滑块作用前的速度，得到作用方向上动量变化进而用动量定理列式求解相关未知量(如例1中的高度，例2中的F)。值得一提的是例2中的作用力方向并非竖直方向，需要用到矢量三角形知识，增加了难度。

在处理“变质量”的“连续”的流体(如水流、空气流等)的问题时，一般先求一段时间内的流体质量，再求作用方向上的动量变化量，利用动量定理表达式中含有的时间量，巧妙把时间这个量处理掉进而求得要求解的物理量。

二、处理变力问题

动量定理的内容为物体在一个过程始末的动量变化量等于它在这个过程中所受力的冲量。动量定理表述了物体所受合外力的冲量与其动量的变化间的关系，其为变力作用及复杂过程问题的处理提供了方法和依据，如电磁感应中的变力、时间未知量问题。这类问题让很多学生束手无策，运用动量定理处理可化繁为简，变力表达式中的某个物理量与时间(可以为未知量)的乘积恰为另一物理量，而这个物理量能通过其他办法求解得出，这样就巧妙地规避了变力无法或难以求解的问题。

【例3】在如图2所示的水平导轨上(摩擦、电阻忽略不计)，有竖直向下的匀强磁场，磁感强度大小为B，导轨左端的间距为L1=4L0，右端间距为L2=L0。今在导轨上放置AC、EF两根导体棒，质量分别为m1=2m0、m2=m0，接在导轨间导体棒电阻R1=4R0，R2=R0。若AC棒以初速度v0向右运动，求AC棒运动的过程中产生的总焦耳热QAC。

图2

【总结】本例题是求AC棒运动的过程中产生的总焦耳热QAC。开始有感应电流产生焦耳热，当两棒产生的动生电动势为零(整体为零)后电路不再产生感应电流也就不再产生焦耳热，在这个过程中安培力是变力不能直接求出克服安培力做功进而得到产生的总焦耳热，需要用能量守恒来求解。接下来关键在于求解两棒最后的速度，而两棒上安培力并非等大反向不能用动量守恒定律处理，应使用动量定理求解。在动量定理表达式中安培力中的电流与时间二者乘积对两棒是一样的，恰好可以消掉，使得安培力变力问题迎刃而解。

三、处理瞬时问题

冲量是个累积量，恒力和给定时间计算冲量是很容易的，但若变力及时间不确定的情况就比较棘手了，这类问题非常考验学生的思维能力、综合处理问题的能力。由动量定理知冲量就等于物体在这个过程始末的动量变化量，将瞬时冲量问题转为求解动量的变化量。

【例4】如图3甲所示，质量m=3.0×10-3kg的“冂”形金属细线框竖直放置在两水银槽中，“冂”形框的水平细杆CD长l=0.20 m，处于磁感应强度大小为B1=1.0 T、方向水平向右的匀强磁场中。有一匝数n=300匝、面积S=0.01 m2的线圈通过开关K与两水银槽相连。线圈处于与线圈平面垂直、沿竖直方向的匀强磁场中，其磁感应强度大小B2随时间t变化的关系如图3乙所示。t=0.22 s时闭合开关K，瞬间细框跳起(细线框跳起瞬间安培力远大于重力)，跳起的最大高度h=0.20 m。不计空气阻力，重力加速度g=10 m/s2，下列说法正确的是

( )

甲

乙

A.0～0.10 s内线圈中的感应电动势大小为3 V

B.开关K闭合瞬间，CD中的电流方向由C到D

C.磁感应强度B2的方向竖直向下

D.开关K闭合瞬间，通过细杆CD的电荷量为0.03 C

【总结】瞬时作用问题一直是物理中的难点，时间短且一般无法得到具体数值，故此类问题不妨先假设作用时间为t，再对这个瞬时过程用物理定理、定律等列等式。在列式中某个量可能恰好跟假设的时间t乘积或者商等构成另一个可求解的物理量，通过这个方式将瞬时时间t变未知为已知，使得问题最终得以解决。如上例3中，安培力表达式中电流与瞬时时间乘积刚好是电荷量，用动量定理刚好巧妙地处理了这个瞬时问题。

四、处理微粒连续作用问题

微粒常指电子流、光子流、微尘等。特点是单个质量m确定，并已知单位体积内的粒子数量n。处理方法为沿运动的方向选取一段微元，柱体的截面积为S，作用时间Δt内的一段微元柱体的长度为Δl=v0Δt，柱体体积ΔV=Sv0Δt，柱体内的粒子数N=nSv0Δt，总质量为mnSv0Δt。根据速度变化可得到动量变化，应用动量定理列式冲量为FΔt，其中Δt可与总质量mnSv0Δt中Δt消掉。

【例5】自动称米机已在粮食工厂中广泛使用，有人认为米流落到秤盘中时有向下的冲量会增大米与秤盘底部作用力，从而增大了分量而不划算；也有人认为自动装置即刻切断米流时，尚有一些米仍在空中，这些米是多给买者的。因而双方争执起来，究竟哪方说的对呢？请分析说明。

【总结】本例题核心在于建立物理模型将米分成三部分(秤盘中、正在接触盘中的部分、空中部分)，最难处理的是正接触落入盘中部分，这部分可以根据下落速度变化用动量定理处理。由称米机出口到秤盘中米堆上表面的高度为h，由机械能守恒得落到米堆表面的初速度，末速度为零，可得到动量的变化量，再对这部分米由动量定理列式。其中这部分米的质量Δm与作用时间Δt的比值恰好为称米机的流量d(题干中已知量)。这类问题很新颖，可与生活实际及高新技术关联，侧重考查学生建模能力以及应用物理知识解决实际问题的综合能力，在此类题中，动量定理是个很得力的工具。