RC框架-HPFRC耗能墙结构侧向刚度计算模型
杨鹏辉, 梁兴文, 何 伟, 辛 力
(1.西安建筑科技大学 建筑设计研究院, 陕西 西安 710055; 2.西安建筑科技大学 土木工程学院, 陕西 西安 710055; 3.中国启源工程设计研究院有限公司, 陕西 西安 710018; 4.中国建筑西北设计研究院有限公司, 陕西 西安 710018)
高性能纤维增强混凝土(HPFRC)具有拉伸应变硬化和多裂缝稳定开展等性能,是理想的耗能材料[1-2].将HPFRC耗能墙装配于钢筋混凝土(RC)框架结构中,形成RC框架-HPFRC耗能墙新型抗震结构.梁兴文等[3]采用拟静力试验研究了这种结构模型的破坏过程、破坏机理、滞回性能、强度退化、刚度退化及耗能能力等特性,结果表明:HPFRC耗能墙可以提高RC框架结构的延性和耗能能力;在罕遇地震作用下,RC框架-HPFRC耗能墙结构仅产生中度损伤;在同一级水平荷载作用下,RC框架与HPFRC耗能墙的损伤程度不同,导致2种构件的截面刚度退化不同步.为明确该结构在水平荷载作用下的基本力学性能,需要分别确定RC框架和HPFRC耗能墙在同一级水平荷载作用时的有效侧向刚度,再将两者的有效侧向刚度按一定的方法进行组合,从而可以得到这种结构的有效侧向刚度.
本文根据2个完全相同的单层、单跨RC框架内分别装配1、2片HPFRC耗能墙所组成的试件FW-1和FW-2的拟静力试验结果[3],并结合其他相关文献的试验研究结果,确定RC框架以及HPFRC耗能墙的刚度退化规律;在此基础上,研究RC框架-HPFRC 耗能墙结构在开裂荷载点、屈服荷载点和峰值荷载点的有效侧向刚度计算模型;最后针对本文的2个试件,用本文所提模型计算的位移值与试验位移值进行对比.
1 RC框架-HPFRC耗能墙结构刚度退化规律
1.1 框架结构刚度退化系数
国内外学者对RC框架结构的刚度退化问题已做过较多研究,日本学者武藤清[4]对两层一跨RC框架模型进行试验研究,得到框架结构在水平荷载作用下的刚度退化规律,如图1所示.图中β为框架刚度退化系数(在任一加载点时的割线刚度与初始刚度的比值);θ为框架的层间侧移角.近年来很多学者在研究RC框架结构的抗震性能时,采用单层、单跨RC框架作为试验对比[5-16],得到了单层、单跨RC框架割线刚度的退化规律.通过对文献[5-16]中13榀单层、单跨RC框架试验数据进行分析,得到试件屈服点割线刚度与开裂点割线刚度比值的平均值为0.54.由图1可见:当位移角为1/136(试验屈服位移角平均值)时,刚度退化系数为0.50,验证了该规律的可靠性.

图1 框架各变形阶段刚度退化Fig.1 Stiffness degradation at various deformation stages
计算平面及竖向均规则的RC结构地震反应时,可将其等效为单自由度体系.Rosenblueth[17]将实际力-位移关系简化为双线性力-位移关系,得到:
(1)
式中:Keff为等效刚度,取最大位移对应的割线刚度,即试件峰值点对应的割线刚度;K0为弹性刚度,因该方法采用双线性力-位移关系,忽略了开裂点的相关特征,即K0实际为结构屈服点对应的割线刚度;α为屈服后刚度与初始弹性刚度之比为;μ为位移延性需求,其值为试件峰值位移μmax与屈服位移μy的比值.
Keff/K0实际反映了试件峰值点相对于屈服点的刚度退化程度.通过对文献[5-16]中的数据进行分析,取α为0.1,计算得到13榀单层、单跨RC框架峰值点割线刚度与屈服点割线刚度的比值Keff/K0的平均值为0.46.由框架屈服点的刚度退化系数,可以得到单层、单跨RC框架峰值点相对于开裂点的刚度退化系数为0.25.
综上,得到单层、单跨RC框架刚度退化规律如图2所示.

图2 单层、单跨RC框架刚度退化规律Fig.2 Stiffness degradation regularity of single-story and single-span RC frame
1.2 HPFRC耗能墙刚度退化规律
根据试件FW-1和FW-2的试验现象[3],分析HPFRC耗能墙暗柱受力纵筋应变可以发现,至试验结束时,大多数暗柱纵筋的应变值接近但均未超过0.002.因此,可以认为试件达到极限承载力时,HPFRC耗能墙即将进入屈服阶段,只需确定HPFRC耗能墙在自身屈服点之前的刚度退化情况.
试件开始加载时,HPFRC耗能墙截面刚度为弹性刚度EwIw;随荷载的增加,耗能墙刚度会按一定规律退化,引入HPFRC耗能墙截面刚度折减系数αw,i,用以考虑耗能墙在不同加载阶段侧向刚度的折减,αw,i在不同受力阶段的具体取值在后续各节中确定.
2 RC框架-HPFRC耗能墙结构各特征荷载点的侧向刚度及位移计算
2.1 RC框架-HPFRC耗能墙结构刚度计算模型
在水平荷载作用下,RC框架与HPFRC耗能墙共同受力,协同变形.计算其侧向刚度时,采用如下假定:
(1)RC框架-HPFRC耗能墙结构所承受的水平荷载由RC框架与HPFRC耗能墙共同承担.
(2)因RC框架内仅局部装配HPFRC耗能墙,故忽略RC框架与HPFRC耗能墙之间的挤压等相互作用,假定这种结构在第i特征荷载点的侧向刚度Ki等于相应特征荷载点RC框架侧向刚度Kf,i与HPFRC耗能墙侧向刚度Kw,i之和:
Ki=Kf,i+Kw,i
(2)
(3)由于HPFRC耗能墙与RC框架上、下梁通过钢板连接件及螺栓连接,故RC框架梁与HPFRC耗能墙之间的连接约束条件不明确.为简化分析,计算耗能墙的侧向刚度时,假定HPFRC耗能墙随RC框架梁仅产生相对水平平动变形,由此产生的误差通过耗能墙刚度折减系数予以考虑.
(4)计算RC框架-HPFRC耗能墙结构各特征荷载点处的侧向刚度时,RC框架与HPFRC耗能墙采用各自的刚度退化系数.设RC框架的侧向刚度退化系数为βf,i,则Kf,i可表示为:
Kf,i=βf,i·Kf,e
(3)
式中:Kf,e为RC框架的弹性侧向刚度.
同理,HPFRC耗能墙的侧向刚度退化规律由刚度退化系数αw,i表达,则Kw,i可表示为:
Kw,i=αw,i·Kw,e
(4)
式中:Kw,e为HPFRC耗能墙的弹性侧向刚度.
2.2 RC框架-HPFRC耗能墙结构在开裂荷载点的有效侧向刚度
2.2.1开裂荷载点RC框架与HPFRC耗能墙的受力状态确定
当试件达到开裂状态时,RC框架柱外侧面出现可见的细微水平裂缝,HPFRC耗能墙墙面及侧面均未出现可见裂缝[3].由此可认为,试件加载至开裂荷载点时,RC框架刚好达到开裂状态,HPFRC耗能墙未达到开裂状态.
2.2.2开裂荷载点RC框架的有效侧向刚度

(5)
(6)
式中:Ec为混凝土的弹性模量;ib和ic分别为框架梁、柱的线刚度;Ib和Ic分别为框架梁、柱的截面惯性矩;Hc和L分别为框架柱的计算高度与梁的计算跨度.
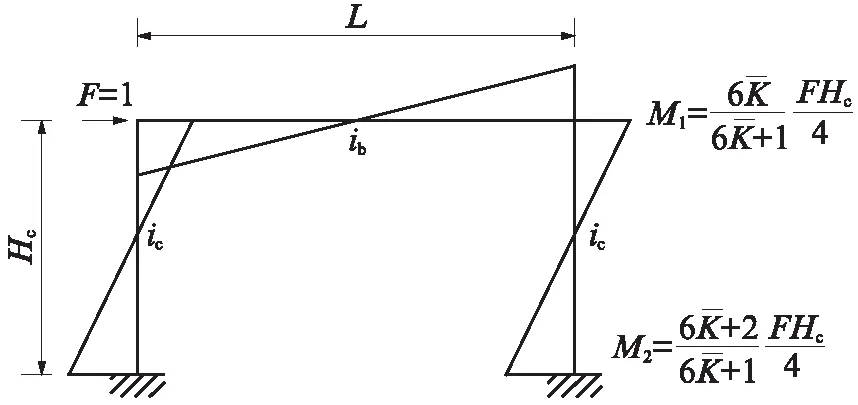
图3 水平荷载作用下单层、单跨RC框架弯矩图Fig.3 Bending moment diagram of single-story and single-span RC frame under horizontal load
由式(5)可得一根单层、单跨RC框架柱的弹性侧向刚度Kc:
(7)
(8)
式中:αc为柱的侧向刚度修正系数.
考虑到RC框架柱在开裂荷载点的截面刚度降低,参考相关文献[18],其开裂点的有效侧向刚度Kf,cr仍按式(7)计算,但其中EcIc需乘以系数0.8.对于本文试验模型而言,其开裂点的侧向刚度Kf,cr为:
Kf,cr=2Kc·αf,cr
(9)
式中:αf,cr为RC框架柱截面刚度折减系数,取0.8.
2.2.3开裂荷载点HPFRC耗能墙的有效侧向刚度
在RC框架-HPFRC耗能墙结构加载至开裂点时,耗能墙未出现肉眼可见裂缝,故可认为耗能墙尚处于弹性阶段,结构在开裂状态时耗能墙的刚度等于相同约束条件下耗能墙的弹性侧向刚度.HPFRC耗能墙通过钢板连接件夹持,并通过高强度螺栓连接,施加到试件顶部的水平荷载通过墙与梁之间的钢板连接件及高强度螺栓传递到耗能墙顶部.为便于装配耗能墙,HPFRC耗能墙与钢板连接件之间、高强度螺栓与螺栓孔之间均留有空隙,故试验加载初期连接钢板与耗能墙内嵌钢板之间产生滑移,从而降低了HPFRC耗能墙提供给试件的侧向刚度,如图4所示.在加载后期,由于HPFRC耗能墙上、下两端螺栓孔处的应力集中,使耗能墙局部损伤,耗能墙上、下两端产生转角,降低了其侧向刚度,如图5所示.考虑以上因素对HPFRC耗能墙侧向刚度产生的削弱作用,引入滑移转角影响系数λ,用以考虑连接件钢板与耗能墙内嵌钢板之间的滑移以及耗能墙两端转动对耗能墙侧向刚度的影响.在荷载控制加载阶段,未观察到HPFRC耗能墙因转角引起的连接件钢板与墙体的滑移;在位移控制加载阶段,可明显观察到两者间因转角引起的相对滑移.因此可以认为,在试件屈服前,λ主要由连接件钢板与耗能墙内嵌钢板之间的水平相对滑移引起,λ取0.45;试件屈服时及屈服后,λ主要由耗能墙上、下两端转动引起,λ取0.15.

图4 连接件与耗能墙内嵌钢板相对滑移Fig.4 Relative slip between connectors and embedded plate of energy dissipation wall

图5 耗能墙上、下两端转动Fig.5 Rotation of two ends of energy dissipation wall
考虑到HPFRC耗能墙在不同加载阶段截面刚度的下降,须引入截面刚度折减系数αw,i.装配于RC框架结构中的HPFRC耗能墙,在水平荷载作用下,其上端随框架梁产生水平平移,与两端仅产生相对平移的连梁(试验中模拟连梁两端仅产生相对平移)的受力状态相似,故可用本课题组之前测试的HPFRC连梁的试验结果[19-20],即用HPFRC 连梁的刚度退化系数来确定本文HPFRC耗能墙的刚度退化系数.经统计分析文献[19-20]的试验结果,可得HPFRC耗能墙各受力阶段截面刚度折减系数αw,i的取值如下:耗能墙开裂前处于弹性阶段,αw,i值可取为0.8;墙体在开裂荷载点处的αw,i值可取为0.55;墙体在屈服荷载点,αw,i值可取为0.40.
由于HPFRC耗能墙的高宽比相对较小,其剪切变形引起的侧移不宜忽略;引入滑移转角影响系数λ和截面刚度折减系数αw,i后,HPFRC耗能墙在开裂荷载点的有效侧向刚度Kw,cr为:
(10)
式中:Hw为HPFRC耗能墙的高度;Ew为HPFRC材料的弹性模量;Gw为HPFRC材料剪切模量,取0.4Ew;Iw和Aw分别为HPFRC耗能墙的截面惯性矩和截面面积;k为截面形状系数,对矩形截面取1.2;λ为滑移转角影响系数,根据试验结果,取0.45;αw,cr为RC框架-HPFRC耗能墙结构在开裂荷载点时HPFRC耗能墙的截面刚度折减系数,取0.8;n为耗能墙的数量.
2.2.4开裂刚度及开裂位移
根据式(2),RC框架-HPFRC耗能墙结构开裂点的有效侧向刚度Kcr为:
Kcr=Kf,cr+Kw,cr
(11)
RC框架-HPFRC耗能墙结构的开裂位移Δcr为:
(12)
式中:Fcr表示RC框架-HPFRC耗能墙结构开裂点处的水平荷载.
2.3 RC框架-HPFRC耗能墙结构在屈服荷载点的有效侧向刚度
2.3.1屈服荷载点RC框架与HPFRC耗能墙受力状态确定
由试验现象可知,当试件加载至屈服荷载点时,框架柱纵向受力钢筋屈服,耗能墙暗柱的纵向受力钢筋均未达到屈服应变,且耗能墙墙面上未出现明显的裂缝.由此可认为试件加载至屈服荷载点时,框架柱刚好达到屈服极限状态,HPFRC耗能墙未达到开裂状态.
2.3.2屈服荷载点RC框架的有效侧向刚度
RC框架-HPFRC耗能墙结构在屈服荷载点时,RC框架刚好达到屈服极限状态,则由式(3)可得RC框架的有效侧向刚度Kf,y:
Kf,y=βf,y·Kf,e
(13)
式中:βf,y为RC框架屈服点的刚度退化系数,由图2可知,该值取0.54.
2.3.3屈服荷载点HPFRC耗能墙的有效侧向刚度
试件加载至屈服荷载点时,耗能墙未出现裂缝;试件屈服后的下一级加载,耗能墙出现大量裂缝.表明试件加载至屈服荷载点时,HPFRC耗能墙虽未观察到肉眼可见的裂缝,但已不再处于弹性阶段.根据式(4),此时HPFRC耗能墙的有效侧向刚度Kw,y由式(14)计算:
(14)
式中:αw,y为RC框架-HPFRC耗能墙结构在屈服荷载点时HPFRC耗能墙的刚度折减系数,考虑到该状态下HPFRC耗能墙未开裂但接近开裂,其取值为0.55;滑移转角影响系数λ取0.15.
2.3.4屈服刚度及屈服位移
根据式(2),RC框架-HPFRC耗能墙结构在屈服荷载点的有效侧向刚度Ky为:
Ky=Kf,y+Kw,y
(15)
RC框架-HPFRC耗能墙结构的屈服位移Δy为:
(16)
式中:Fy表示RC框架-HPFRC耗能墙结构屈服点的水平荷载.
2.4 RC框架-HPFRC耗能墙结构在峰值荷载点的有效侧向刚度
2.4.1峰值荷载点RC框架与HPFRC耗能墙受力状态的确定
在峰值荷载点的前一级加载下,仅右柱外侧角部混凝土保护层开始有被压酥的迹象;试件加载至峰值荷载时,左、右两柱外侧面及左柱内侧面混凝土均被压碎,保护层脱落,表明柱底受压区边缘混凝土已达到其极限压应变,框架柱底截面已至最大承载力,此时HPFRC耗能墙有大量裂缝产生,但暗柱纵筋未屈服.故认为RC框架-HPFRC耗能墙结构加载至峰值荷载点时,RC框架刚好达到最大承载力,HPFRC耗能墙已超过开裂极限状态,但未达到屈服极限状态.
2.4.2峰值荷载点RC框架的有效侧向刚度
在RC框架-HPFRC耗能墙结构中,由于HPFRC耗能墙的存在,增加了RC框架在屈服后的延性,使结构中RC框架的峰值位移滞后于单层、单跨RC空框架的峰值位移,故考虑框架峰值位移滞后的影响,须引入位移延性影响系数η.通过对文献[5-16]中的数据分析,可得13榀单层、单跨RC空框架位移处性需求μ的平均值为2.77.本文试件中RC框架位移处性需求μ的平均值为3.83.由数据对比可得到,试件峰值荷载点割线刚度与单层、单跨RC空框架峰值点割线刚度的比值为0.72,故可将位移延性影响系数η取为0.7.

(17)
式中:Kf,p为单层、单跨RC空框架峰值点割线刚度;βf,p为单层、单跨RC空框架峰值点刚度退化系数,由图2可知,该值取0.25.
2.4.3峰值荷载点HPFRC耗能墙的有效侧向刚度
当RC框架-HPFRC耗能墙结构加载至峰值荷载点时,HPFRC耗能墙已超过开裂极限状态,未达到但接近屈服极限状态.试件加载至峰值荷载点时,HPFRC耗能墙的截面刚度折减系数为αw,p,则此时HPFRC耗能墙的有效侧向刚度Kw,p为:
(18)
式中:滑移转角影响系数λ取0.15;刚度折减系数αw,p取0.40.
2.4.4峰值荷载点的有效侧向刚度及位移
根据式(2),RC框架-HPFRC耗能墙结构在峰值荷载点的有效侧向刚度Kp为:
(19)
RC框架-HPFRC耗能墙结构峰值荷载点的位移Δp为:
(20)
式中:Fp表示RC框架-HPFRC耗能墙结构峰值点的水平荷载.
2.5 计算结果与试验结果的对比
试件特征荷载点所对应的RC框架与HPFRC耗能墙的受力状态如表1所示.在确定试件各特征点的受力状态后,采用侧向刚度和位移计算公式,根据文献[3]中表3的相关数据,计算得到试件在顶部水平荷载作用下开裂荷载点、屈服荷载点和峰值荷载点的位移,特征荷载点位移的计算值与试验值对比如表2所示.由表2可见:各特征荷载点位移计算值与试验值吻合较好,表明本文的刚度计算模型较为合理.

表1 试件特征荷载点对应的RC框架与HPFRC耗能墙的受力状态Table 1 Stress state of RC frame and HPFRC energy dissipation wall at characteristic load points

表2 特征荷载点位移计算值与试验值对比Table 2 Comparison between calculated value and experimental results of lateral displacement at characteristic load points
3 结论
(1)RC框架-HPFRC耗能墙结构中的RC框架与HPFRC耗能墙是由性能差异较大的材料制作,故在相同的特征荷载点(如开裂、屈服、峰值等荷载点)处,2种构件的损伤状态和刚度退化程度明显不同,HPFRC耗能墙比RC框架的刚度退化缓慢很多.计算这种结构的水平承载力和侧向刚度时,应考虑这种差异.
(2)RC框架-HPFRC耗能墙结构中RC框架的刚度退化规律,主要取决于结构的受力状态和材料性能退化;而HPFRC耗能墙的刚度退化规律除与结构的受力状态和材料性能退化有关外,尚与耗能墙上、下端和框架梁的连接构造有关.因此,本文提出的HPFRC耗能墙在各特征荷载点的刚度折减系数,仅适用于本文的连接构造情况.
(3)基于RC框架和HPFRC耗能墙的刚度退化规律建立的有效侧向刚度计算模型,基本上反映了这种结构的受力和变形特点,按此模型所得的结构位移计算值与试验值基本吻合.但由于试验数据较少,本文方法的可靠性有待进一步试验验证.

