一种液性塑料的薄壁类零件磨削夹具的设计

刘建刚，杜风娇

(1.武夷学院 机电工程学院，福建 南平 354300;2.浙江理工大学 机械与自动控制学院，浙江 杭州 310018)

0 引言

薄壁零件在磨削外圆加工过程中，因其刚度低，易产生变形，从而影响薄壁零件的加工精度.为了保证薄壁类零件的加工精度，一些研究者提出了使用夹具的方法.例如：黄华宾[1]针对异形腔薄壁壳体零件的加工特征,制作了一种工装夹具,该夹具可有效提高装卸工件的效率.张珂等[2]提出了一种用于线束接插件的自动化夹具的优化方法，该方法可将原加工中0.2 mm的变形量降低到0.1 mm以下.杜风娇等[3]利用蛇形弹簧设计了一套薄壁套筒类零件磨削夹具，但作者未对该方案开展动平衡实验，因此采用该方案加工的零件表面有可能产生振动波纹.杨志源等[4]通过设计多自由度夹具有效地解决了薄壁类零件加工时装夹定位困难的问题.目前为止，学者对液性塑料夹具方面的研究大多仅限于理论分析和辅助测量等[5-8]，而对其具体设计和可靠性研究得较少.如文献[9]设计了一款液性塑料夹具用于加工连杆零件，该夹具方案虽能够保证零件的位置尺寸，但当压力过大时会有少许液性塑料从活塞与芯轴的间隙中漏出.基于上述研究，本文以液压凿岩机套阀阀芯为例，利用液性塑料设计一种薄壁套筒类零件外圆磨削夹具，并通过仿真验证本文提出方法的可行性.

1 夹具设计

1.1 工艺要求

图1为套阀阀芯的设计图.由图1可知,Φ 36、Φ 40、Φ 42、Φ 44的外圆表面需要有较高的同轴度和较低的粗糙度.Φ 36、Φ 40、Φ 42、Φ 44表面的加工工艺图如图2所示.由图2可知，产品的设计要求为：以套阀阀芯内径(Φ 42)为定位基准A，Φ 40和Φ 44的外圆相对A基准的同轴度为Φ 0.01 mm，Φ 40、Φ 44 的外圆表面粗糙度为0.4 μm.

图1 套阀阀芯的设计图

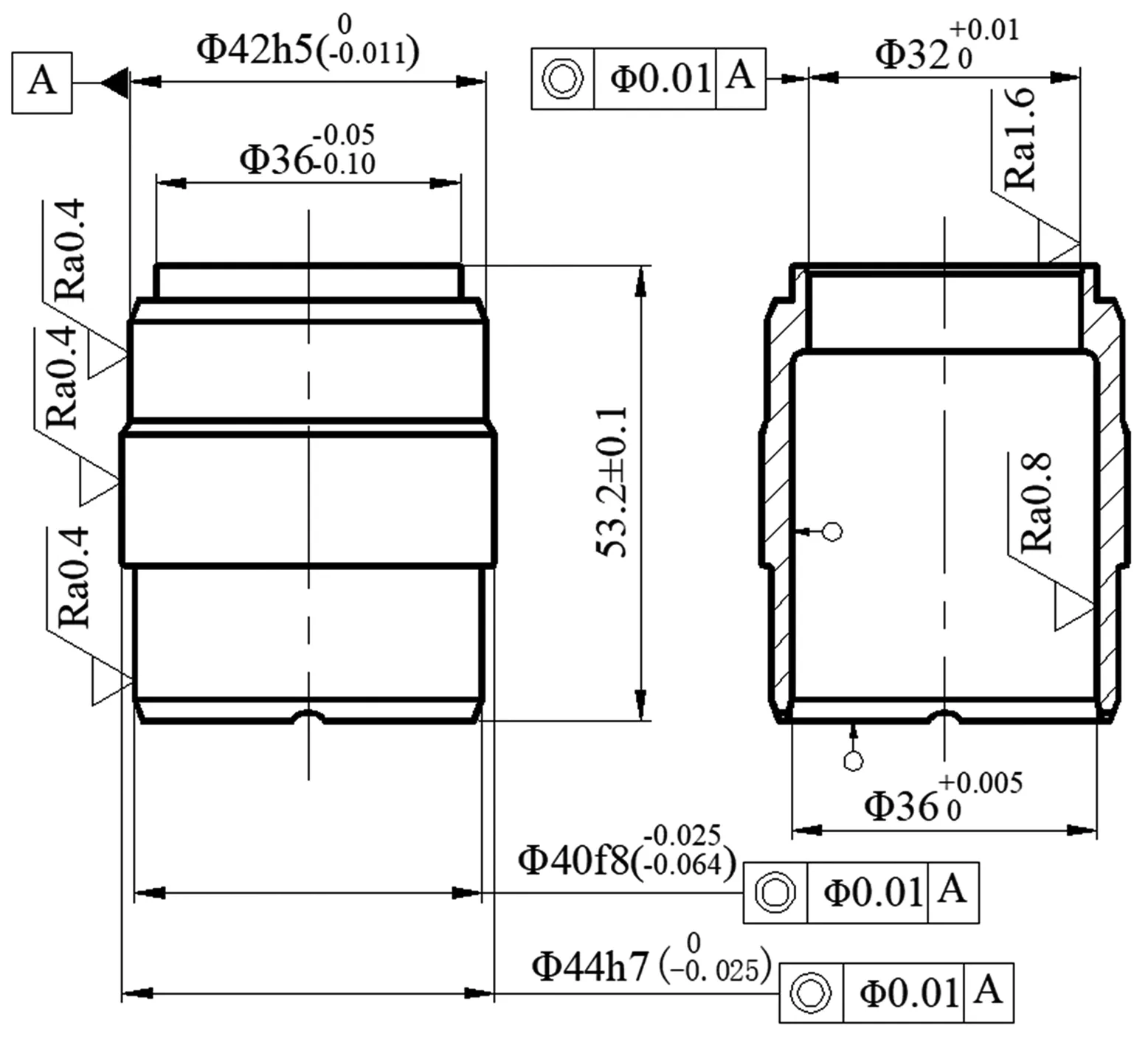
图2 套阀阀芯的加工工艺图

1.2 夹具的设计原理和组装

图3为本文设计的夹具装配示意图，其工作方式为：在薄壁套筒内，由芯轴、芯轴II、柱塞、薄壁套和加压螺钉形成一个密封腔；液性塑料将其在密封腔内受到的压强(由柱塞拧紧力压迫而产生的)均匀地传递给薄壁套，薄壁套受到挤压后产生径向变形并挤压套阀阀芯，从而达到限制套阀阀芯旋转的目的.

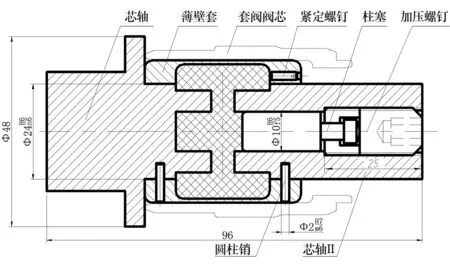
图3 夹具装配示意图

薄壁套(见图4)为夹具的关键零件，其最大外径尺寸为Φ 36.为保证夹具使用的稳定性，本文在设计薄壁套时，将其左、右端面的平行度和粗糙度设置为0.4 μm，内圆的粗糙度设置为0.4 μm，外圆Φ 36处的圆跳动值设置为0.02 mm.

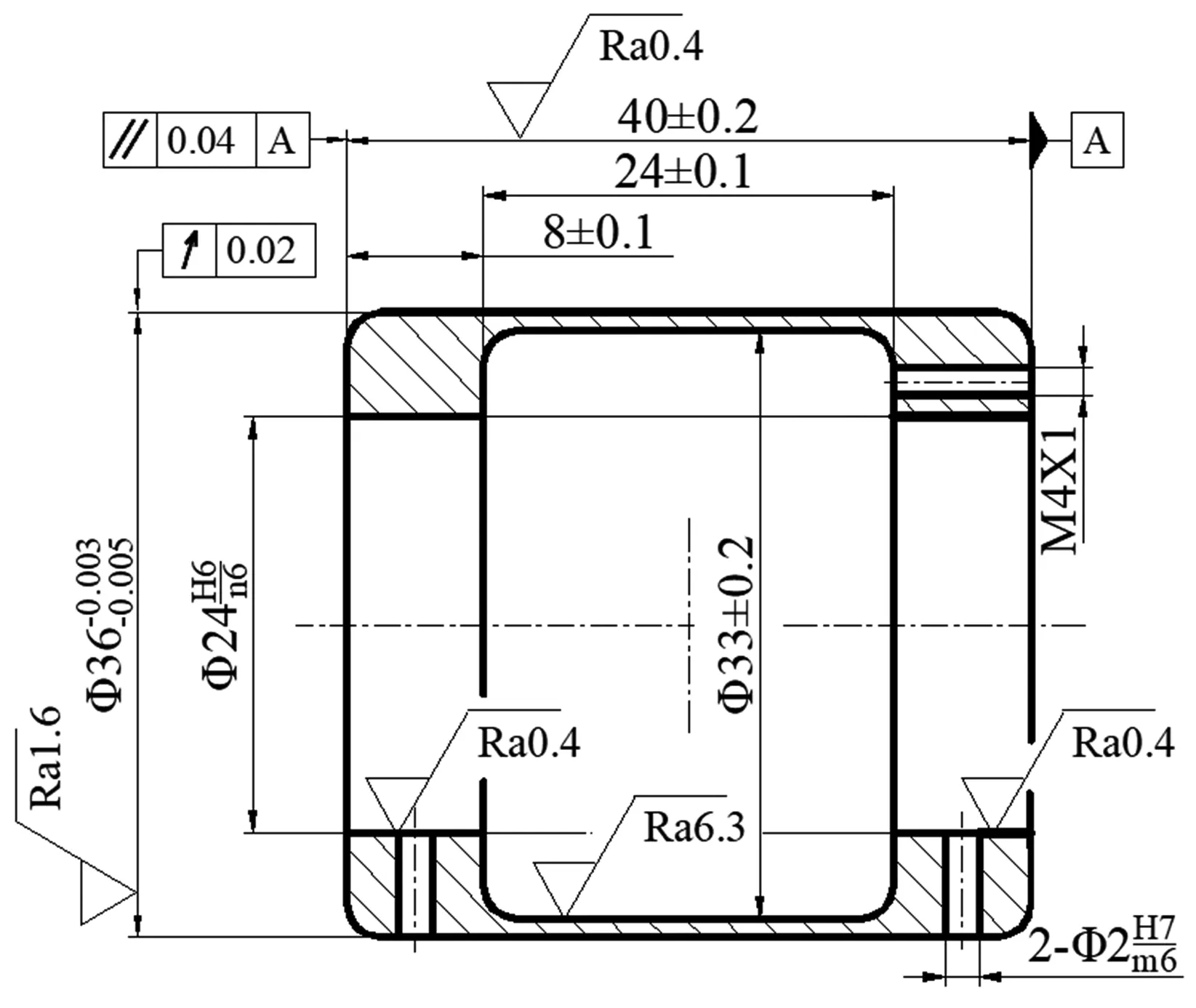
图4 薄壁套示意图

1.3 夹具使用步骤

夹具的使用步骤为：①通过圆柱销将薄壁套、芯轴及芯轴Ⅱ固定,并形成一个开放的容积腔；②通过芯轴Ⅱ内孔将液性塑料注入至开放的容积腔内；③通过加压螺钉和柱塞使液性塑料所在的容积腔变成一个密封腔；④通过拧紧加压螺钉使柱塞轴向移动，以此压紧液性塑料.

2 理论计算与仿真

2.1 理论计算

薄壁套选取65Mn，套阀阀芯选取40Cr，假设套阀阀芯外圆磨削产生的摩擦力为200 N(经验值)[3].通过对薄壁套进行有限元仿真(结果见图5 —图7)可知，当密封腔内的压强达到7.44 MPa时，薄壁套与套阀阀芯接触产生过盈配合，此时的薄壁套外表面最大应力值为101.78 MPa，套阀阀芯内的表面最大应力值为25.22 MPa.根据文献[11]，本文将套阀阀芯与薄壁套之间的摩察系数设置为0.2，由此可得薄壁套与套阀阀芯之间的摩擦力Ff=25.22×π×0.182×0.04=205.3 N>200 N，此时拧紧螺塞所需的轴向力为F=P×S=186 N.

螺栓拧紧力矩-轴向力关系的表达式[11]为

(1)

式中：M为螺栓拧紧力矩(N·m)；F为螺栓轴向力(N)；d2为M12粗牙螺纹中径，d2=10.86 mm；λ为螺纹升角(°)，λ=arctg(t/d2)，t为螺距(mm)，λ=60°；f为螺母与被连接件支撑面间的摩擦系数，f=0.2；ρ为螺旋副的当量摩擦角,ρ=24.8°;tgρ为螺旋副的当量摩擦系数，tgρ=f′/cosβ，其中β为三角型螺纹半角(β=30°),f′为螺旋副间的摩擦系数；R为M10粗牙螺纹大径，R=12 mm；r为M10粗牙螺纹小径，r=10.11 mm.由式(1)计算可得，芯轴Ⅱ右端面的加压螺钉的拧紧力矩M为2.58 N·m时，柱塞产生的轴向力为186 N，密封腔内液性塑料承受的压强为7.44 MPa.

2.2 仿真分析

对薄壁套进行仿真得到的应力图、变形图和应变图如图5 —图7所示.由图5 —图7可知：薄壁套的应力峰值为101.78 MPa，薄壁套的变形峰值为0.007 7 mm，薄壁套的应变值为0.000 51 mm.由薄壁套所用材料(65Mn)的屈服极限(430 MPa)可知，薄壁套不会发生塑性破坏，即材料满足设计要求.

图5 薄壁套的应力图

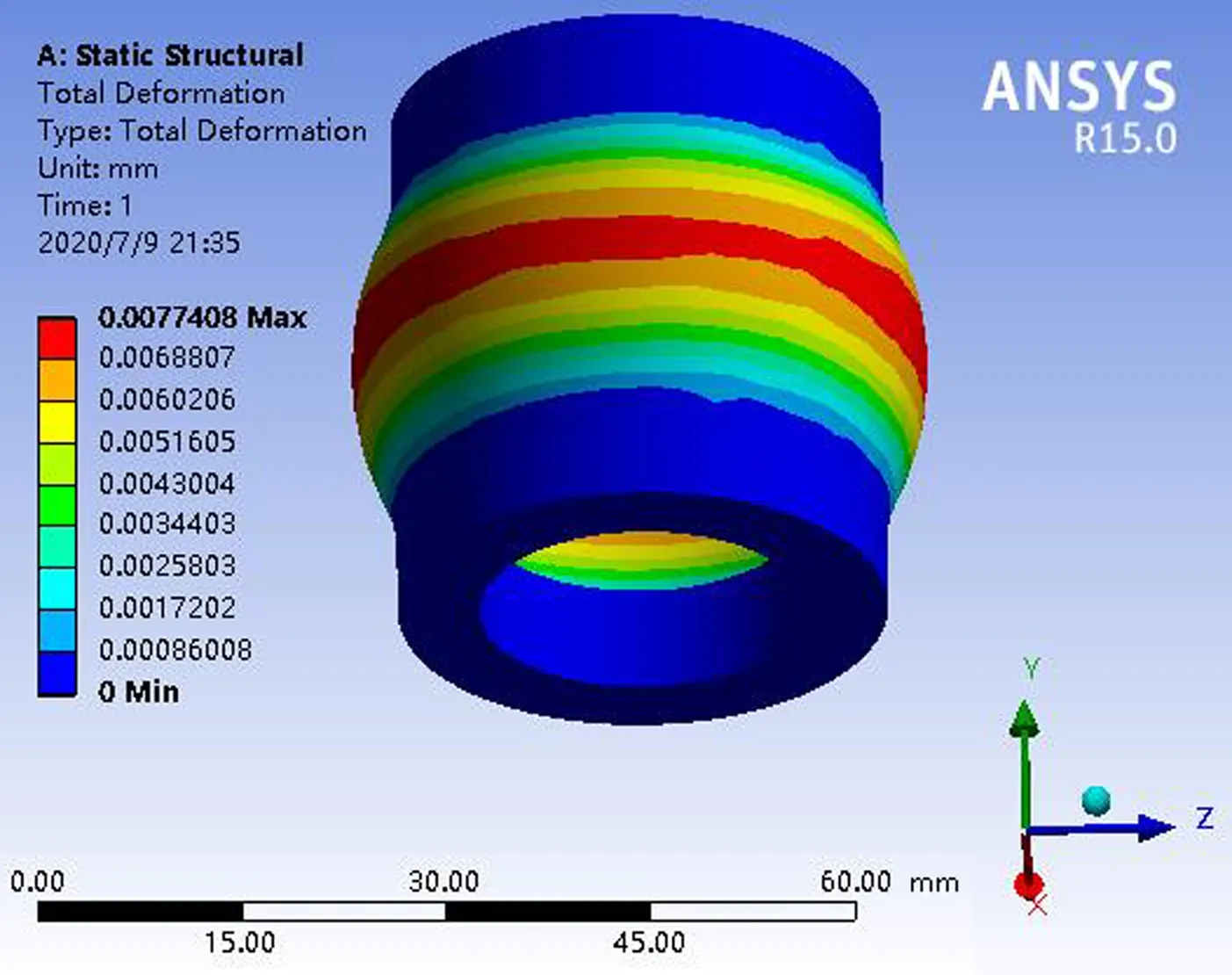
图6 薄壁套的总变形图

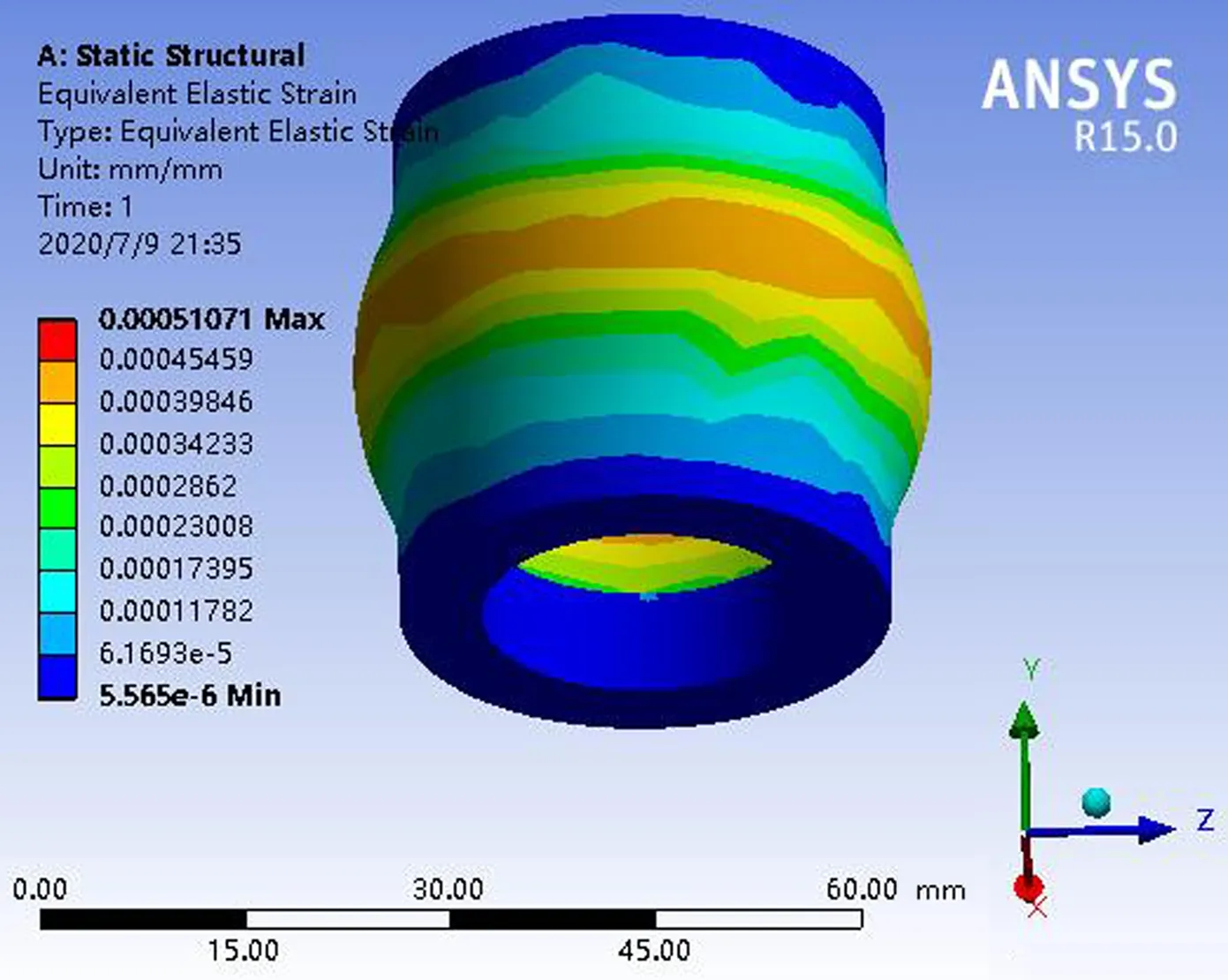
图7 薄壁套的应变图

对套阀阀芯进行仿真得到的应力图、变形图和应变图如图8 —图10所示.由图8 —图10可知：套阀阀芯的应力峰值出现在套阀阀芯与薄壁套(Φ 36)的配合处，为25.22 MPa；套阀阀芯的径向变形峰值为0.002 1 mm，套阀阀芯的径向应变峰值为0.000 13 mm.由套阀阀芯所用材料(40Cr)的屈服极限(785 MPa)可知，材料满足设计要求.

图8 套阀阀芯的应力图

图9 套阀阀芯的变形图

图10 套阀阀芯的应变图

3 夹具可靠性分析

3.1 套阀阀芯磨削的可靠性分析

根据2.1中的计算可知，套阀阀芯与薄壁套之间的摩擦力(205.3 N)大于外圆磨削时产生的摩擦力(经验值为200 N)，因此磨削过程不会产生打滑现象，即套阀阀芯磨削夹具的磨削力满足设计要求.

3.2 薄壁套应力的可靠性分析

薄壁套应力的标准正态分布的计算公式[12]为

(2)

式中：μF为材料的许用强度[14]，μF=430 MPa；μS为薄壁套所受应力值，μS=11.9～101.78 MPa；σS为应力分布标准差，为6.1 MPa(由文献[12]中的经验公式计算所得)；σF为强度标准差，σF=26.24.由式(2)计算得z=-12.2.根据正态分布表[14]可知，薄壁套的应力可靠度为100%，失效率为0.

4 结论

本文设计了一种基于液性塑料的薄壁类零件磨削夹具，对其进行理论计算显示，密封腔内的压强达到7.44 MPa时即可克服套阀阀芯外圆磨削所产生的摩擦力，此时加压螺钉所需的扭矩为2.58 N·m.对薄壁套及套阀阀芯的可靠度进行仿真验证表明，本文设计的薄壁套筒类零件磨削夹具的应力可靠度为100%，因此本文方法对提高薄壁类零件的制造精度具有很好的参考价值.本文在研究中因条件限制，未能对装配后的夹具进行动平衡实验，且未能考虑液性塑料的热膨胀对夹紧力的影响，因此今后我们将对本文方案开展动平衡实验，并对液性塑料的热膨胀进行研究，以提高本文方法的可靠性和适用性.