钢管混凝土格构式风电平面塔架的行为参数分析
闻 洋, 王洪泽
(内蒙古科技大学 土木工程学院, 内蒙古 包头 014010)
近年来,中国风电产业发展迅速,目前已位居世界第一位.但其核心技术和关键设备仍需依靠国外引进.虽然在空气动力学、控制理论等相关风能转化的机械设备领域已具备自主研发能力,但在同等重要的塔架结构形式、受力、可靠性等方面研究较少.现有塔架的结构形式、设计方法和标准全完照搬国外标准,缺乏符合中国实际风况和环境条件的标准.
实际工程中的风电机塔架形式主要有锥筒混凝土塔架和钢格构式塔架等.与锥筒混凝土塔架相比,钢格构式塔架具有强度高、刚度高、材料利用率高以及运输与安装方便等特点,已成为风电塔架的优先选择,具有广阔的应用前景[1].闻洋等[2]通过对格构式塔架管板节点进行静力加载,发现节点承载力随塔柱径厚比的增加而下降;刘香等[3]研究了格构式钢管混凝土结构用于风电塔架时,塔架钢管混凝土立柱的强度、刚度和稳定性,并给出了其计算公式.但塔架构件较多,受力较复杂,一个构件的破坏往往导致整个结构的失效,且塔架设计中构件参数的确定依据不明,控制参数对塔架在地震作用下的变化规律缺乏理论指导[4-5].基于此,闻洋等[6-8]提出了钢管混凝土格构式风电塔架,完成了钢管混凝土格构式风电塔架的性能研究与设计.为了研究钢管混凝土格构式风电平面塔架在地震作用下的破坏机理和受力性能,对平面塔架进行了低周反复试验,并对其滞回曲线、骨架曲线和刚度退化曲线进行了分析,采用Abaqus有限元软件进行验证并对参数管径比和壁厚比进行了拓展分析,进一步完善了钢管混凝土格构式风电平面塔架设计内容,可为该结构体系规范的制定提供参考依据.
1 试验概况
1.1 原材料及试件设计
塔架模型的塔柱及腹杆均采用20#热轧无缝钢管,塔柱钢管内填充普通C30混凝土,钢材及混凝土的力学性能指标见表1.取塔架原型顶部3层,根据相似理论[7]得到钢管混凝土格构式风电塔架平面模型.由于场地条件和加载装置的限制,对塔架平面模型进行1∶3.15[8]的缩尺,塔柱截面尺寸为φ108×4mm,柱脚与基础采用刚性连接[9].为研究腹杆截面尺寸对塔架受力性能的影响规律,以腹杆与塔柱直径的比值(管径比t)和壁厚比b为变化参数,确定腹杆尺寸为φ32×3、φ42×3、φ42×5mm.腹杆与腹杆、腹杆与塔柱的连接方式为相贯式[10],其中斜腹杆均为1根连续、1根在连接处中断,试件主要参数见表2.

表1 钢材及混凝土的力学性能指标Table 1 Mechanical properties of steel and concrete
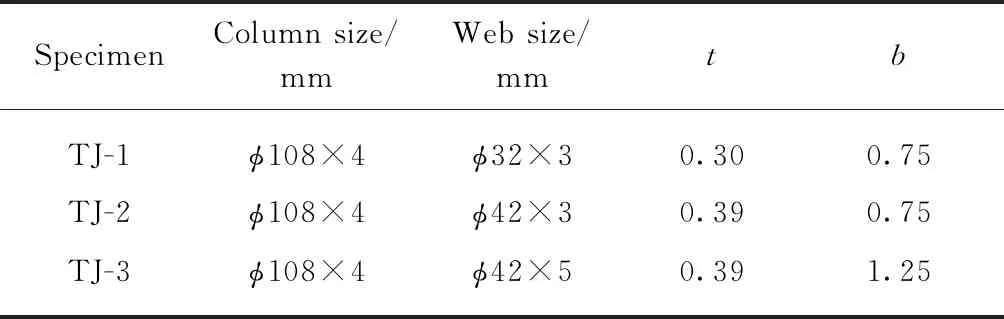
表2 试件主要参数Table 2 Main parameters of specimens
1.2 加载制度
塔架模型通过4根地脚螺栓固定,保证试件在加载过程中不发生滑移,并防止试件在加载过程中发生倾覆;安装水平侧向支撑,防止加载过程中产生平面外的变形;伺服作动器一边与加载板相连,另一边与反力墙相连,调整伺服作动器位置保证其作用力方向和顶层腹杆平行,通过固定在反力墙上的伺服作动器对顶层节点施加水平荷载,加载装置示意图见图1.
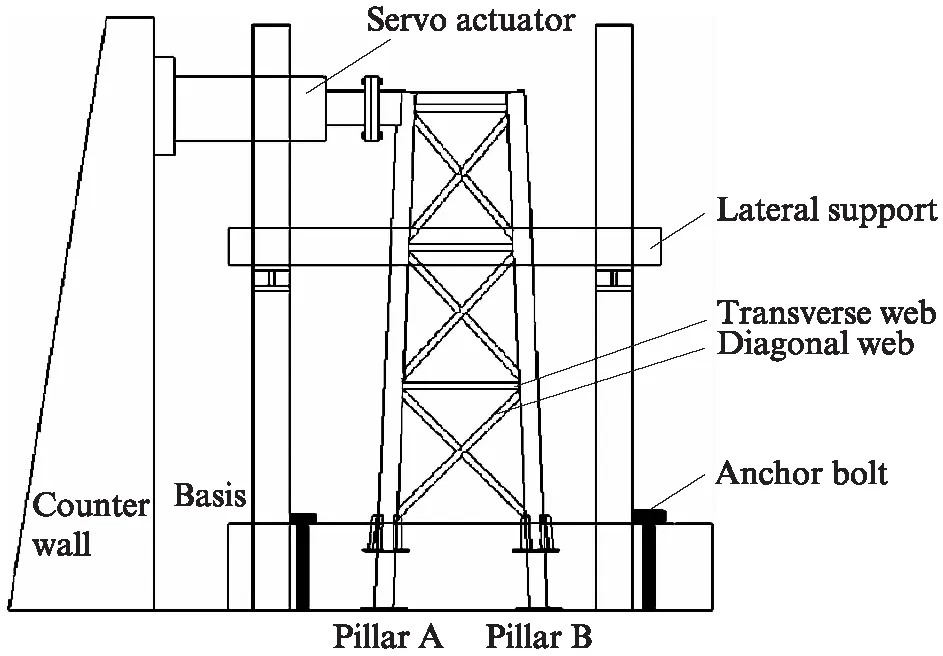
图1 加载装置示意图Fig.1 Schematic of loading device
对钢管混凝土格构式风电平面塔架施加无竖向力的低周反复水平荷载,试验采用力-位移混合控制加载制度[11].在结构屈服以前采用荷载控制,屈服之后采用位移控制,屈服前每级荷载增量为20kN,每级循环1次;在结构屈服以后,按照结构屈服位移(Δy)的0.25倍为级差进行分级加载,反复循环3次,直至某级加载的第1循环低于最大荷载值的85%时,停止试验.
2 破坏特征
试件的破坏形态见图2.由图2可见:TJ-1的破坏形态为横腹杆与塔架连接处断裂;TJ-2的破坏形态为连续斜腹杆屈曲破坏;TJ-3的破坏形态为塔柱的断裂.

图2 试件破坏形态Fig.2 Failure patterns of specimen
TJ-1试件在加载初期处于弹性工作阶段,随着循环荷载的不断增大,在低周反复荷载作用下试件出现了残余变形,此时认为顶层受拉斜腹杆已经纵向屈服,此时的屈服位移为12mm.之后试件进入塑性阶段,此时采用位移控制加载:当正向加载到18mm 时,听到有焊缝撕裂的声音,顶层受拉腹杆与受压腹杆连接处出现轻微裂纹;反向加载时,此前的受拉腹杆转变为受压腹杆,原先的焊缝裂纹逐渐闭合,此时顶层腹杆与塔柱连接处出现轻微裂缝,当反向加载到19mm时,中间层腹杆开始出现与顶层类似的裂缝,继续加载可以看到顶部腹杆与塔柱连接处焊缝逐渐扩大;当反向加载加载到24mm时,顶层腹杆与塔柱连接处突然断裂,构件刚度瞬间下降,塔架内力发生重分布,试件破坏.
TJ-2试件在加载初期阶段,变形和荷载呈正比例稳定增长,当正向加载中间层受压斜腹杆纵向应变(ε)达到1600×10-6时,卸载时已经存在残余变形,认为试件已经屈服,此时的屈服位移为13mm.之后试件进入塑性阶段,采用位移控制加载:当反向加载位移达到15mm时,顶层受拉斜腹杆在连接焊缝处开始出现轻微裂缝;当反向加载到21mm时,连续腹杆在腹杆连接处受到双向荷载的作用被压陷;当反向加载到33mm时,顶层非连续腹杆处焊缝完全断开,正向荷载下降到80kN,此时连续腹杆屈曲非常严重,试件完全破坏.
TJ-3在加载初期,试件处于弹性工作阶段,随着荷载的不断增大,底层塔柱纵向屈服,此时的位移为18mm.之后试件进入塑性阶段,采用位移控制加载:当反向加载到35mm时,中间层受拉斜腹杆连接处焊缝撕裂,导致荷载突然下降;当反向加载到40mm时,底层受拉斜腹杆连接处焊缝撕裂,底层水平腹杆与受压塔柱在节点处沿焊缝撕裂;继续加载,当正向加载到45mm时,底层塔柱在底层节点冠点处开始出现轻微裂缝并逐渐环向发展;随着循环荷载的增大,当正向加载到50mm时,底层塔柱节点裂缝已经基本贯通整个塔柱,表明试件已经破坏.
对比TJ-1和TJ-2的破坏特点:TJ-1顶层受拉斜腹杆最先屈服,屈服位移为12mm,TJ-2中间层受拉斜腹杆最先屈服,屈服位移为13mm,管径比对试件屈服位移的影响很小,只提高了8.3%;由于TJ-2管径比较大,在腹杆四周的焊缝长度可以得到保证,所以试件的破坏位置也不相同.对比TJ-2和TJ-3的破坏特点:TJ-3底层塔柱纵向屈服,屈服位移为18mm,说明壁厚比对试件的屈服位移影响较大,屈服位移提高了50.0%;从破坏位置来看较高的壁厚比对腹杆的受力有较为明显的改善.
3 试验结果分析
3.1 试验滞回曲线
图3中红色实线为试验得到的试件在反复荷载作用下形成的滞回曲线.由图3可见:3个试件的试验滞回曲线形状都不是理想的梭形;随着加载的进行,构件损伤逐渐增加,塑性位移逐渐增大,峰值荷载逐渐减小,试验滞回曲线所围面积越来越大,这表明试件随着刚度的退化,构件的耗能能力在逐渐增加;TJ-1试件在荷载控制阶段,试验滞回曲线所有点都通过原点,曲线近似重合成1条直线,此时试件的初始弹性刚度无变化,弹性工作阶段的峰值荷载达到85kN,进入屈服阶段后荷载由位移控制,正向加载时峰值荷载逐渐下降,塑性屈服位移逐渐增大,试件只在最后1个滞回环发生轻微捏缩现象,此时极限荷载为70kN,极限位移为27mm;TJ-1试件反向加载时峰值荷载在试件屈服前期没有明显变化,在顶层腹杆与塔柱连接处断裂时,荷载急剧减小,塑性位移急剧增大,这是由于试件焊缝的破坏导致试件传力机制发生变化,刚度急剧减小,塔柱侧移严重,此时的峰值荷载为55kN,极限位移为28mm,最终的滞回曲线形状类似半理想状态的“弓形”;TJ-2试件在荷载控制阶段,试验滞回曲线形状同TJ-1,但其峰值荷载达到了125kN,在进入塑性阶段以后,正向加载时极限位移可以达到33mm,反向加载过程中顶层非连续腹杆处焊缝完全断开时承载力瞬间降至60kN,塑性位移陡升至20mm,最终的试验滞回曲线形状呈“反S形”;TJ-3试件在荷载控制阶段和前2个试件一样,峰值荷载达到了170kN,在进入到塑性阶段以后,位移控制阶段时,正向加载下曲线的峰值荷载在位移达到45mm时仍然没有明显下降,反向加载后在屈服位移为35mm时,荷载和塑性位移发生突变,此时的峰值荷载为75kN,塑性位移为52mm,试件破坏时的曲线形状呈“反S形”.

图3 试件在反复荷载作用下的试验和Abaqus有限元分析模拟滞回曲线Fig.3 Experimental and Abaqus finite element analysis simulation hysteresis curves of specimens under repeated loads
对比TJ-1和TJ-2试件:TJ-1的试验滞回曲线形状更加饱满;正向加载时,TJ-2峰值荷载和极限位移更高,相比TJ-1分别提高了47.1%和22.2%;反向加载时,TJ-2的峰值荷载和极限位移分别提高了14.5%和22.2%.由此可见,高管径比试件虽然在滞回曲线形状上不如低管径比试件饱满,受试件滑移的影响也更大,但其具有更高的承载能力和塑性位移,使管径比较高的试件所围面积较大,具有更好的耗能能力.对比TJ-2和TJ-3试件:TJ-3在正向加载时峰值荷载和极限位移比TJ-2提高了30.8%和45.5%;反向加载时,TJ-3的峰值荷载和极限位移分别提高了42.9%和57.6%.壁厚比较高的试件表现出受滑移影响更严重,试验滞回曲线在“反S形”和“Z形”之间,曲线形状不够饱满,但是高壁厚比试件具有更高的承载能力和塑性位移,试验滞回曲线所围面积大于低壁厚比试件,说明高壁厚比试件具有更高的耗能能力.
3.2 骨架曲线
试件的骨架曲线见图4.由图4可见:所有试件的骨架曲线均较为完整,有明显的上升段、峰值段和下降段,在试件屈服以前3条曲线基本重合,这说明管径比和壁厚比的变化并没有对试件的初始刚度产生影响;在正向加载阶段,TJ-1在位移为11mm时率先达到屈服,并随着位移的增加很快达到峰值点,继续增加位移可以看到荷载立即下降,当极限位移为28mm时宣告试件破坏,TJ-2在达到屈服位移后随着位移的增加峰值荷载缓慢下降,TJ-3在达到屈服位移后荷载还能略有上升,当塑性位移在20mm到50mm之间可以一直保持在峰值,当塑性位移为56mm 时试件破坏;在反向加载阶段,试件TJ-1、TJ-2、TJ-3分别在塑性位移为24、25、29mm时曲线出现拐点,此时的荷载分别为117、121、185kN,这是由于塔架腹杆和塔柱的破坏造成了塔架内力重分布,此时塔架刚度急剧下降,塑性位移陡升.
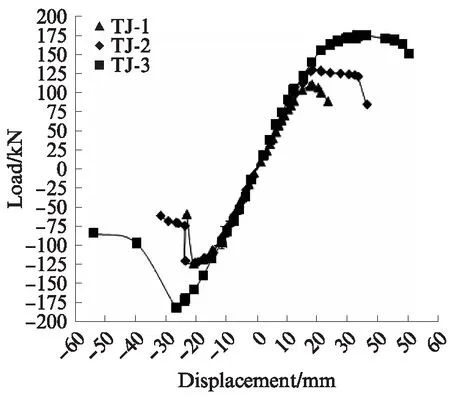
图4 试件的骨架曲线Fig.4 Skeleton curves of specimens
对比TJ-1和TJ-2试件:在正向加载阶段,TJ-2的峰值荷载和极限位移比TJ-1提高了18.2%和44.4%,并且随着位移的增加峰值荷载下降较为缓慢,说明TJ-1后期变形能力较差,这是因为达到峰值荷载后顶层与中间层腹杆失效,塔柱绕底层塔柱节点发生转动;在反向加载阶段,TJ-2的峰值荷载和极限位移比TJ-1提高了3.4%和33.3%.由此可见,低荷载情况下不同管径比的试件对初始弹性刚度影响很小,但是在高荷载情况下,管径比较大的试件具更好的延性,且对承载能力影响较小.对比TJ-2和TJ-3试件:在正向加载阶段,TJ-3的峰值荷载和极限位移比TJ-1分别提高了50.0%和47.4%,并且具有更长的塑性发展阶段;反向加载阶段TJ-3的峰值荷载和极限位移比TJ-1分别提高了50.0%和61.8%,主要是由于壁厚比的增大,塔柱外部钢管开始对核心混凝土发挥约束作用,使其处于三向受压状态,外部钢管与核心混凝土之间协同互补,共同工作提高了试件变形能力与稳定性.由此可见,壁厚比对试件的性能影响比较大,在高荷载情况下壁厚比较大的试件承载能力提高明显,延性也大幅度提高.
3.3 刚度退化曲线
图5为试件的刚度(K)退化曲线.由图5可知:3个试件在弹性阶段刚度退化平缓,并且曲线斜率近似相同;随着加载位移的增大,试件刚度开始加速退化,曲线斜率急剧下降;TJ-1初始刚度最低,为7.4kN/mm,曲线在塑性位移为14mm时出现了拐点,之后刚度退化速度明显加快,破坏时刚度为2.8kN/mm;TJ-2初始刚度为7.5kN/mm,曲线在塑性位移为22mm时出现拐点,破坏时的刚度为2.2kN/mm;TJ-3初始刚度为8.5kN/mm,曲线在30mm处出现拐点,破坏时刚度为2.1kN/mm.
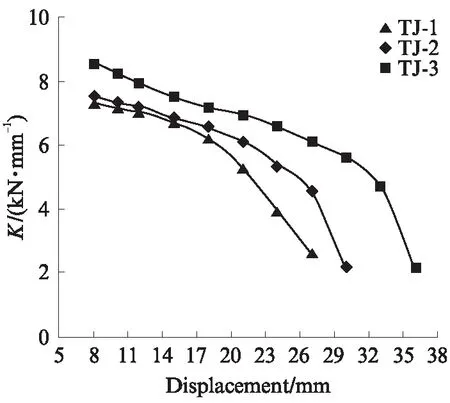
图5 试件的刚度退化曲线Fig.5 Stiffness degradation curves of specimens
对比试件TJ-1和TJ-2:TJ-2初始刚度比TJ-1提高了1.4%;在弹性阶段的刚度退化曲线两者基本吻合,拐点处塑性位移提高了57.1%;拐点后TJ-2的刚度退化曲线下降更快,TJ-2破坏时的刚度也比TJ-1降低了21.4%.这说明管径比较高的试件在试件屈服前期的刚度退化和低管径比试件基本相同,随着屈服位移的不断加大,管径比较高的试件刚度退化速度较慢,但是当塑性位移达到拐点时会急剧下降刚度退化速度甚至超过低管径比试件.对比TJ-2和TJ-3:TJ-3初始刚度比TJ-1提高了13.3%;在弹性阶段两者斜率近似相等,拐点处塑性位移提高了36.4%;在拐点之后两者斜率相等,破坏时刚度降低了4.5%.由此可见,壁厚比较高的试件具有更高的初始刚度,刚度曲线斜率和低管径比大体相同,在刚度急速下降的塑性位移点也较壁厚比低的试件更大.
4 有限元分析
为了与试验结果进行对比分析,并进一步深入探讨各参数指标对节点受力性能和破坏机理的影响规律,采用ABAQUS软件对平面塔架进行有限元分析.
4.1 材料本构关系及界面处理
试验中塔柱管壁、腹杆等构件的厚度与长度之比均小于1/15,属于壳单元类型中的薄壳问题,可以忽略沿厚度方向的应力.对于薄壳问题常规单元的性能要优于连续体壳单元,本文中塔柱管壁和腹杆选用四节点四边形有限薄膜减缩积分壳单元(S4R),沿厚度方向默认划分5个单元积分点,核心混凝土采用八节点六面体缩减积分实体单元(C3D8R)[12].
有限元分析中钢材本构模型采用韩林海提出的二次塑流本构模型,弹性模量和屈服强度以及泊松比取自材料性能试验,混凝土的本构模型选用塑性损伤模型来模拟混凝土的非弹性行为.钢材与混凝土的接触在切向采用“罚”摩擦,界面摩擦系数取0.4,在法向采用硬接触,使接触面间的压力大小不受限制.腹杆所有的焊缝连接均采用Tie约束[13-14].
4.2 有限元分析结果与试验结果对比
有限元模拟与试件破坏形态的应力云图见图6,其中Smises为米塞斯应力.由图6可见:试件实际的破坏形态为塔架中部腹杆连接部位,在低周反复荷载作用下发生的焊缝破坏,此时焊缝已经完全撕裂,腹杆在焊缝连接部位出现了明显的屈曲现象;而由Abaqus有限元软件所得到的应力云图中,高应力区在腹杆焊缝连接部位,腹杆在高应力区发生了严重的屈曲.

图6 有限元模拟与试验破坏形态的应力云图Fig.6 Finite element simulation and test stress nephogram of failure mode morphology
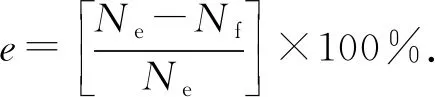
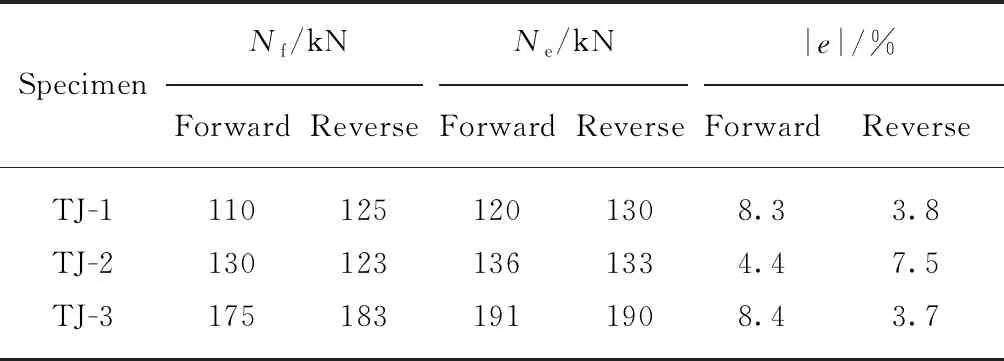
表3 峰值载荷试验值与Abaqus模拟值对比Table 3 Comparison of peak load test values and Abaqus simulation values
图3中蓝色虚线为Abaqus有限元分析模拟滞回曲线.由图3可见:3个试件的模拟滞回曲线都呈现理想的饱满“梭形”,比试验滞回曲线所围面积大,反映出试件的塑性变形能力比较强;模拟和试验滞回曲线存在较大差距,这主要是由于在进行模拟计算时,首先模拟本构输入的材料本构关系数据无法精确反映试件材料性能,尤其是混凝土这种离散性较大的材料,其次焊缝质量的影响,Abaqus在腹杆连接处所采用的连接为Tie约束,默认腹杆在此处焊缝不会发生破坏,但是实际过程中由于试件尺寸过小焊缝长度不够导致焊缝位置处焊接质量难以保证;TJ-1在正向加载阶段,峰值荷载的模拟值和试验值相差很小,在极限位移方面模拟值可以达到31mm,大于试验值,这是由于焊缝处腹杆发生屈曲失稳而失效;TJ-1在反向加载阶段,模拟极限荷载、极限位移也和试验值相差不大,但是卸载时模拟值具有更大的残余变形,这种残余变形随着循环次数的增加呈近似线性增大,而模拟值曲线是连续变化且没有突变点,这是因为模拟时焊缝并没有发生破坏,试件的传力途径也是连续变化的;TJ-2在正向加载阶段极限荷载和极限位移相差不大,但是在反向加载阶段,模拟曲线捏缩现象不明显;TJ-3和TJ-2模拟曲线大体相同但TJ-3曲线更加饱满,具有更好的耗能能力,在试件屈服位移达到40mm以上时,仍然具有良好的承载能力.
综上,在破坏形态方面试验现象和模拟结果基本吻合,在峰值荷载方面试验值和模拟值相差很小,在滞回曲线方面模拟曲线更加饱满.这是由于实际试件中的焊接残余应力会对构件的塑性变形产生影响,而对峰值荷载影响很小.因此,可以认为采用本文建立的有限元模型能较准确地模拟钢管混凝土格构式风电平面塔架的力学行为.
4.3 拓展参数分析
4.3.1管径比分析
设置塔柱尺寸为φ108×4mm,腹杆尺寸分别为φ32×4、φ38×4、φ45×4、φ50×4mm,得到的试件管径比b分别为0.30、0.35、0.42、0.46,试件壁厚比t=1.0.不同管径比下试件的荷载-位移模拟曲线见图7.由图7可见:4条曲线形状大体相同,都有明显的上升段、峰值段和下降段;弹性阶段,管径比为0.46的试件初始刚度最大,分别比管径比为0.30、0.35、0.42的试件高63.4%、24.1%、4.2%;进入屈服阶段后,与管径比为0.30、0.35、0.42的试件相比,管径比为0.46的试件的屈服位移分别高23.1%、23.1%、6.3%,峰值荷载分别高76.9%、53.3%、21.1%,极限位移分别高93.5%、46.3%、9.1%.随着管径比的增加,试件的屈服位移、峰值荷载和极限位移都会提高,但是提高幅度不同,在管径比b>0.42时提高幅度较小.综合考虑经济性与实用性,工程中建议管径比b的取值范围在0.42左右.
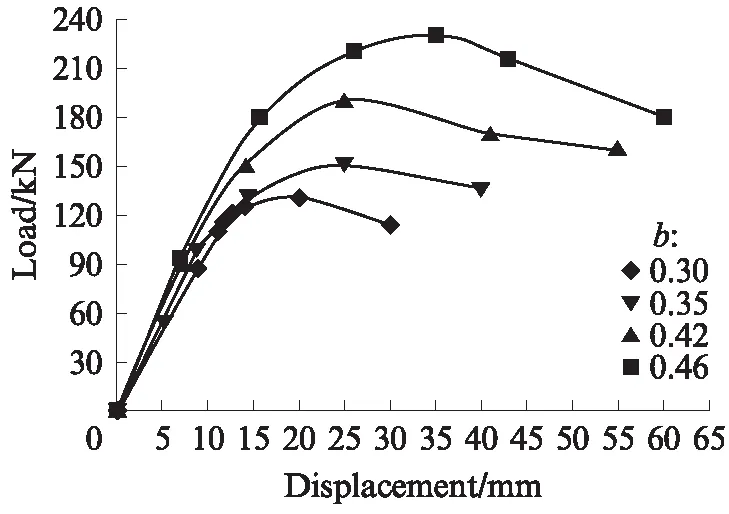
图7 不同管径比下试件的荷载-位移模拟曲线Fig.7 Load-displacement simulation curves of specimens with different tube diameter ratios
4.3.2壁厚比分析
设置塔柱尺寸为φ108×4mm,腹杆尺寸分别为φ32×2、φ32×3、φ32×5、φ32×6、φ32×7mm,得到的试件壁厚比分别为0.50、0.75、1.25、1.50、1.75,试件管径比b=0.3.
不同壁厚比试件的荷载-位移模拟曲线见图8.由图8可见:5条曲线形状大体相同,都有明显的上升段、峰值段和下降段;曲线随着壁厚比的增加荷载峰值点逐渐右移,屈服位移逐渐增大;在弹性阶段,壁厚比为1.75的试件初始刚度最大,分别比壁厚比为0.50、0.75、1.25、1.50的试件高51.7%、32.0%、9.1%、3.9%;在进入屈服阶段后,与壁厚比为0.50、0.75、1.25、1.50的试件相比,壁厚比为1.75的试件屈服位移分别高60.0%、33.3%、15.4%、15.4%,峰值荷载分别高136.6%、68.6%、27.2%、15.8%,极限位移分别高117.4%、61.3%、25.0%、11.1%.随着试件壁厚比的增大,试件的屈服位移、峰值荷载和极限位移都增大,但是增大幅度不同,在壁厚比t>1.25时增大的幅度较小.综合考虑经济性与实用性,工程中建议管径比t的取值范围在1.25左右.

图8 不同壁厚比试件的荷载-位移模拟曲线Fig.8 Load-displacement simulation curve of specimens with different wall thickness ratios
5 结论
(1)3组试件破坏模式分别为:TJ-1顶层腹杆与塔柱连接处发生强度破坏;TJ-2顶层交叉节点连接处非连续腹杆的弯曲失稳破坏;TJ-3底层塔柱节点冠点位置发生强度破坏.
(2)管径比对试件承载能力和极限位移影响不大,试件管径比较高的试件比管径比较低的试件滞回曲线所围面积更大,耗能能力更强;提高壁厚比可以有效提高承载能力和极限位移,壁厚比较高的试件比壁厚比较低的试件滞回曲线所围面积更大,耗能能力更强.
(3)由骨架曲线得出提高壁厚比要比提高管径比对极限承载力的提高更为有效,提高管径比和壁厚比都会提高试件的极限位移.由刚度退化曲线得出提高管径比对提高初始刚度和延缓刚度退化速度效果不明显,提高壁厚比可以显著提高初始刚度和减缓刚度退化速度.
(4)试件管径比b≤0.42或壁厚比t≤1.25时,试件的屈服位移、峰值荷载、极限位移增长速度较快;而在管径比b>0.42或壁厚比t>1.25时提高的幅度较小.综合考虑经济性与实用性,工程中建议管径比b的取值范围在0.42左右,管径比t的取值范围在1.25左右.

