基于ANUSPLIN的京津冀区域逐日气温格点数据集建立方法研究

刘焕莉，范增禄，韩明稚，田国强

(河北省气象信息中心，河北 石家庄 050021)

引言

空间插值是基于已知采样点的数据预测未知空间(点)数据值的过程[1]。目前，常用的空间插值方法有反距离加权法、趋势面法、克里金插值法、薄盘样条插值法等, 以及形式多样的多元线性回归方法等[2]，上述插值方法在本质上均基于一定的统计学模型，但在空间化模拟过程中各有不足，其差别主要表现在适用性、插值原理、空间分辨率等方面[3]。因此，通过比较而选择一个合适的、适用于数据空间分布特点的插值方法是空间插值的关键[4]。

20世纪90年代以来，以ANUSPLIN专用空间插值软件为代表的区域精细化插值方法在国内外得到广泛应用[5-14]。如钱永兰等[15]利用ANUSPLIN软件对中国境内667个基本、基准地面气象观测站1961—2006年逐日气温和降水数据进行插值，并将插值结果分别与反向距离权重法和克里金法插值结果进行对比，结果证明ANUSPLIN插值法对降水的插值误差较另外两种方法略大，而气温的插值效果则优于反向距离权重法和克里金法。刘志红等[16]选择黄土高原中北部多沙粗砂区为研究区，利用ANUSPLIN方法对研究区内52个气象站近21 a月平均多种气象要素进行插值，结果证明在所有气象要素中，温度的空间插值误差最小，风速、水汽压的误差中等，日照时数和降雨量的误差较大。空间内插的精度与台站分布密度息息相关，赵煜飞等[17]分析了不同台站密集度情况下插值的精度大小，得出台站密集程度越高，插值效果越好的结论。廖荣伟等[18]利用ANUSPLIN、SHERPAD和OI插值方法对中国地面气温数据进行了网格化并对插值精度进行了比较，得出了考虑高程的ANUSPLIN插值的综合评价较好。

以上研究多是基于长时间序列的国家级地面气象观测站气象要素进行插值，数据集空间分辨率多为0.5°×0.5°和0.1°×0.1°，高空间分辨率的格点数据具有规范的格式、易于分析、能更精细地表征空间分布特征等优点[19]。鉴于温度、降水等要素具有明显的局地小气候特征[20]，需要高空间密度的观测站点来捕获数据，本文选取京津冀区域以及临近省共3 974个国家级及区域气象观测站，利用ANUSPLIN插值软件对2018年汛期6—8月逐日气温资料进行插值，得到了京津冀区域逐日气温0.01°×0.01°格点数据集，并对数据集的质量进行检验评估。

1 研究区域及数据来源

1.1 研究区域

研究区域选择京津冀地区(图1)，京津冀地区位于华北平原北部，行政区域包括北京、天津、雄安新区及河北，地域面积21.6万km2，位于113.5°～120°E，36°～42.3°N。西倚太行山与山西省为邻；北部与内蒙古自治区接壤；南部与河南、山东两省毗邻；东与辽宁省相接。京津冀区域地貌类型多样，平原、丘陵、盆地、山地、高原等地貌类型尽在其中，整体地势呈现西北高东南低的地形特点。区域内海拔2 000 m以上的山峰有10座，第一高峰位于张家口小五台山东台，海拔2 882 m[21-22]。

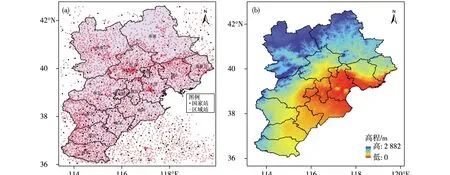
图1 研究区示意图(a.国家级和区域气象观测站分布；b.高程，填色，单位：m)

1.2 数据来源

本文研究所使用的数据为113.4°～120°E，36°～42.5°N范围内2018年6—8月京津冀区域2 402个站点的逐日气温数据，为减弱边界效应造成的插值误差，引入临近省区(内蒙古、山西、山东、河南、辽宁)1 572个站点数据。数据来源于河北省气象信息共享平台，数据内容包括台站经纬度、海拔高度和日平均气温。数据的准确性对插值结果影响显著，因此原始数据均经过格式检查、缺测检查、界限值检查、内部一致性检查、时变检查、持续性检查等质量控制。

由于气温的空间分布与地形特征紧密相连，采用ANUSPLIN软件对研究区2018年6—8月逐日气温进行空间插值，为提高空间插值精度，减弱地形条件对气温空间插值精度的影响，真实反映研究区域气温的时空分布规律，引入高程数据DEM[23]，分辨率为1 km，通过数字高程模型提取地形特征因子(如海拔高度、坡向、坡度、地形遮蔽度等)，利用ArcGIS将DEM数据转化成ASCII格式，作为协变量参与空间插值运算。

2 研究方法

2.1 空间插值方法

本文采用ANUSPLIN专用空间插值软件对京津冀区域气温站点资料进行空间插值，为评估ANUSPLIN软件的插值效果，以日平均气温为研究对象，综合比较基于多种插值方法的插值精度，确定最适合京津冀地区气温的插值方法。

2.1.1 ANUSPLIN插值

ANUSPLIN软件是基于普通薄盘和局部薄盘样条函数对多变量数据进行内插的工具，能同时进行多个表面的空间插值，适用于时间序列的气象数据。ANUSPLIN软件提供了完整的统计分析、数据诊断等功能，同时也支持多种数据输入和表面查询功能。

局部薄盘光滑样条(partial thin plate smoothing splines)是对薄盘光滑样条原型的扩展[24], 它除普通的样条自变量外允许引入线性协变量子模型, 如温度和海拔之间、降水和海岸线的关系等[25]。

局部薄盘光滑样条的理论统计模型为：

zi=f(xi)+bTyi+ei(i=1,…,N)

(1)

式中：zi是位于空间i点的因变量；xi是独立变量，f是要估算的关于xi的未知光滑函数；yi为独立协变量；b为yi的系数；ei为随机误差。

函数f和系数b通过公式(2)的值最小来获得，即由最小二乘法估计来确定：

(2)

其中Jm(f)是函数f(xi)的粗糙度测算函数，定义为f的m阶偏导，ρ为光滑参数，在数据保真度与曲面的粗糙度之间起平衡作用，在ANUSPLIN中通常用广义交叉验证GCV的最小化以及最大似然法GML的最小化来确定。

ANUSPLIN程序共分为8个程序模块(SPLINA，SPLINB，SELNOT，ADDNOT，DELNOT，GCVGML，LAPPNT，LAPGRD)。通过输入固定格式的数据文件，包含站号、经度、纬度、高程信息(DEM数据)，再执行ANUSPLIN中的内置模块函数，最终输出插值后的数据结果，同时包含光滑参数RHO、拟合数据误差列表文件(均值、标准差、方差等)、拟合表面系数的协方差矩阵、误差表面等。薄盘光滑样条总共有18种插值模型选择 (独立变量、协变量和样条次数多种组合) 见表1，根据不同气象要素选择合适插值模型。

ANUSPLIN最佳模型判断标准：GCV或GML最小；信噪比最小；信号自由度小于站点的一半，但不能过小以至于寻找不到最优光滑参数；模型成功率判断中无“*”。

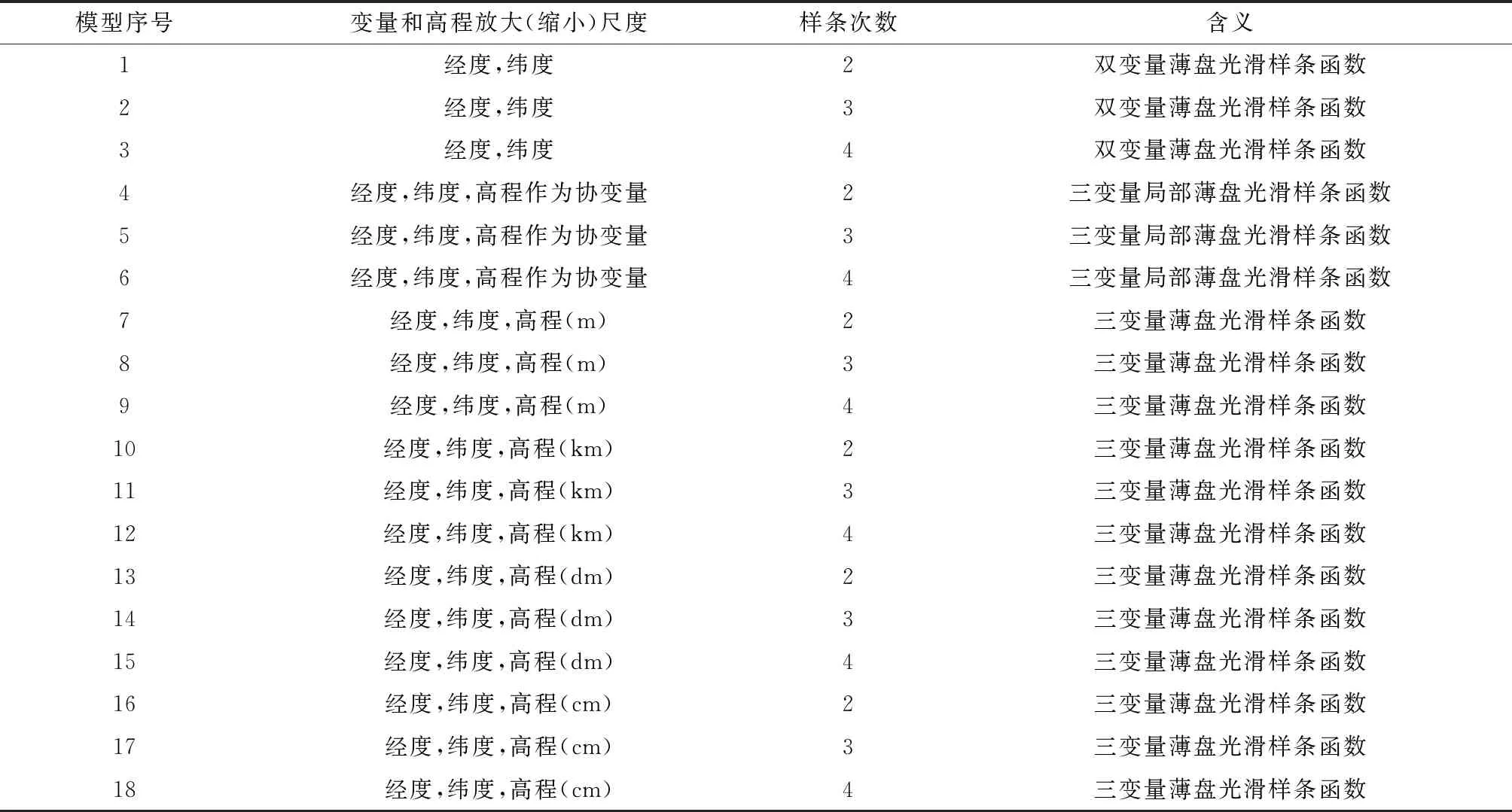
表1 薄盘光滑样条函数模型

2.1.2 反距离权重方法

反距离权重插值基于相似相近原理，即两个物体离得越近，它们的值越相似，反之，则相似性越小。反距离权重(inverse distance weighted，IDW)方法以插值点和样点的距离为权重进行加权平均[26]，算法如下：

(3)

式中：z为估算值；zi为第di个样点的观测值；di为插值点到第i个样点的距离；n为参与插值的样点数目；p为用于计算距离权重的幂指数,一般p=2。

IDW是根据点数据生成栅格图层的常用方法，但它易受样本点极值的影响，计算中常出现一种孤立点数据明显高于周围数据点的情况，即“牛眼”现象。

2.1.3 普通克里金法

普通克里金(ordinary kriging,OK)法是从地统计学的克里格法中演化出的一种插值方法，它以区域性变量理论为基础，半变异函数为分析工具，其实质是利用半变异函数对未知样点进行线性无偏、最优估计。它不仅考虑预测点位置与已知数据位置的相互关系，而且还考虑变量的空间相关性[8]。算法如下：

(4)

(5)

式中：z(x0)为x0点的预测值，z(xi)为xi点的测量值，λi为测量值对预测值的权重系数。

普通克里金法的优点是可估计测试参数的空间变异分布以及估计参数的方差分布，但计算步骤繁琐，计算量大，且变异函数需要根据经验人为选定。

2.1.4 样条函数法

样条函数(spline function， SPLINE)法主要通过估计方差，利用一些特征节点，用多项式拟合的方法来产生平滑的插值曲线[27]。算法如下：

(6)

样条函数插值法具有易操作，插值速度快的优点，但存在插值后误差不能直接估计，采样点稀少时效果不好的缺点。

2.2 评估指标

为评估ANUSPLIN的插值效果，选取空间分布均匀的15%站点作为检验站点(检验站点不参与插值)，剩余站点作为插值站点，检验站点分布见图2。分别使用IDW、OK、SPLINE和ANUSPLIN进行插值，使用最近距离法将插值的高分辨率资料匹配到京津冀区域各站点上，得到了逐日气温空间插值数据集及实测数据集，采用相关系数(Corr)、平均绝对误差(mean absolute error，MAE)、平均相对误差(mean relative error，MRE)等作为评估插值效果的指标，讨论不同方法对气温插值结果的影响。

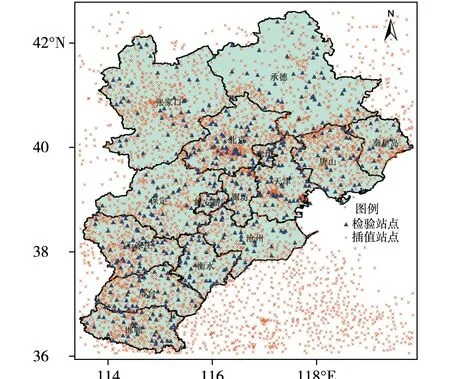
图2 插值站点与检验站点分布

3 结果与分析

3.1 插值结果与分析

依据ANUSPLIN最佳插值模型判断标准，筛选出模型7、模型8、模型9为最优待用模型，再分别用三个待用模型进行插值，分析其误差分布，确定气温的最优插值模型为模型8。

图3为采用4种空间插值方法构建的6、7、8月每月1日的京津冀区域气温空间分布图，通过比较可以发现，ANUSPLIN体现了引入DEM预测气温的优势，插值结果光滑，清晰反映出气温过渡变化的特点，而IDW、OK、SPLINE在曲线平滑程度以及局部地区的空间分布具有一定差异，其中IDW、SPLINE插值结果容易产生“牛眼”现象。因此，在选取插值方法时，应充分考虑空间特异性，引入适当的影响因子，充分分析数据，才能对特定环境下的气象要素进行精确、合理的插值[28]。

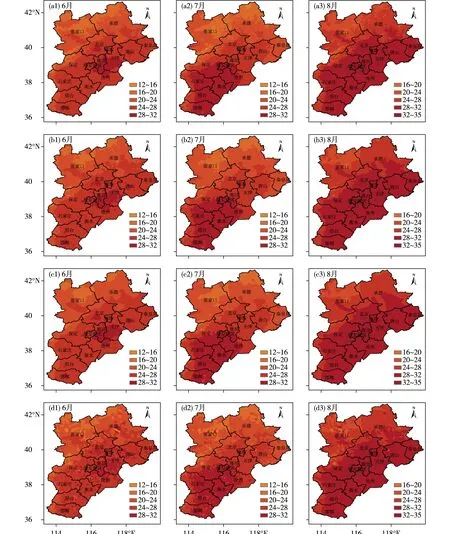
图3 日平均气温空间分布(a. ANUSPLIN, b. IDW, c. OK, d. SPLINE；单位：℃)

综上所述，4种插值方法获得的格点化气温数据均能直观体现京津冀区域气温由北向南递增的空间分布特征，气温分界线沿太行山脉、燕山山脉，分界线以北区域温度较以南平原地区气温低，日气温最大值均出现在低海拔平原地区，而最小值均出现在崇礼围场高海拔地区，日气温整体呈现东南高西北低的趋势。究其原因是在影响气温分布的诸多因素中，以海拔高度和地形影响最显著[29-30]。

3.2 评估结果与分析

相关系数(Corr)可以用来表征预测值与实测值之间的相似程度，用误差占比、MAE、MRE作为评估指标来检验插值精度。相关系数检验结果如下：由图4可以看出，4种插值方法得出的预测值与实测值相关性均较好，相关系数均大于0.86，ANUSPLIN相关系数高于其他3种插值法，相关系数平均达0.97，IDW、OK次之，相关系数平均达0.96，而SPLINE略低，相关系数平均达0.95。

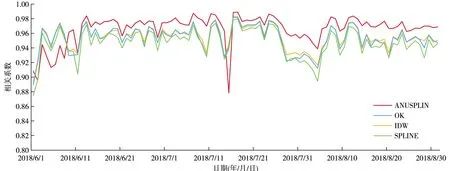
图4 基于不同插值方法的相关系数分布(红色线为ANUSPLIN，蓝色线为OK，黄色线为IDW，绿色线为SPLINE)

基于IDW、OK、SPLINE和ANUSPLIN软件插值的结果有一定差距，通过计算预测值与实测值的误差占比、MAE、MRE作为检验插值精度的标准，可以看出，不同插值方法的MAE、MRE、误差占比并不相同(图5、图6、表2)。由表2可见，4种插值方法中，基于ANUSPLIN软件的插值结果最优，其次为IDW、OK，基于SPLINE的气温插值结果最差。

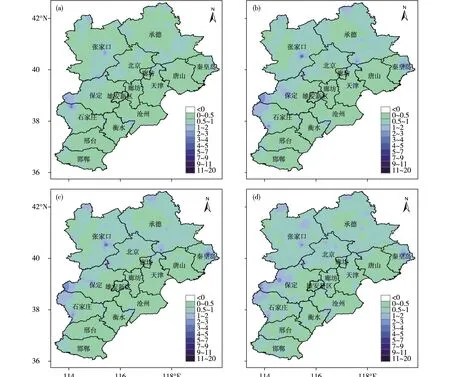
图5 平均绝对误差空间分布(a. ANUSPLIN, b. IDW, c. OK, d. SPLINE；单位：℃)

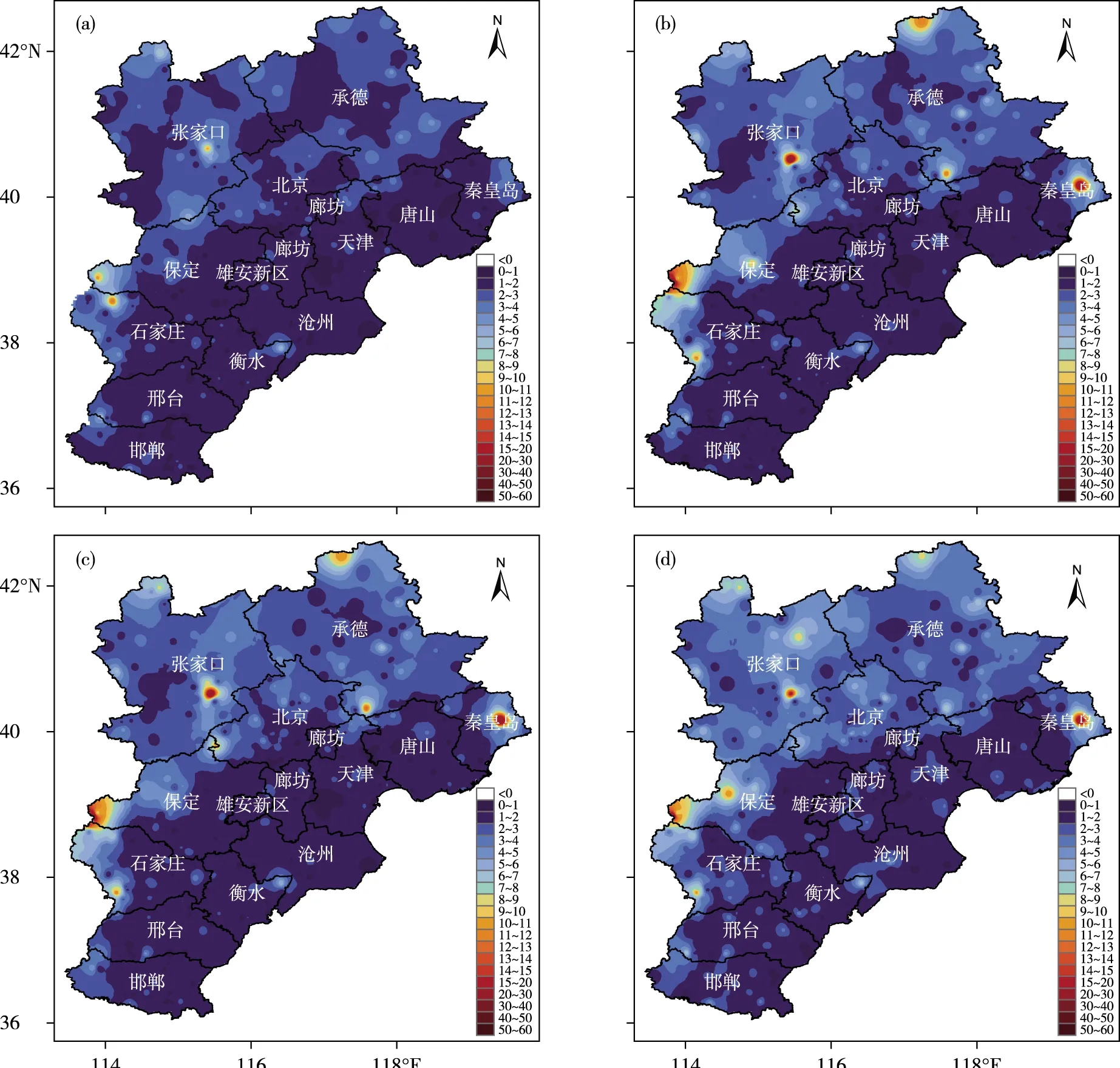
图6 平均相对误差空间分布(a. ANUSPLIN, b. IDW, c. OK, d. SPLINE；单位：%)

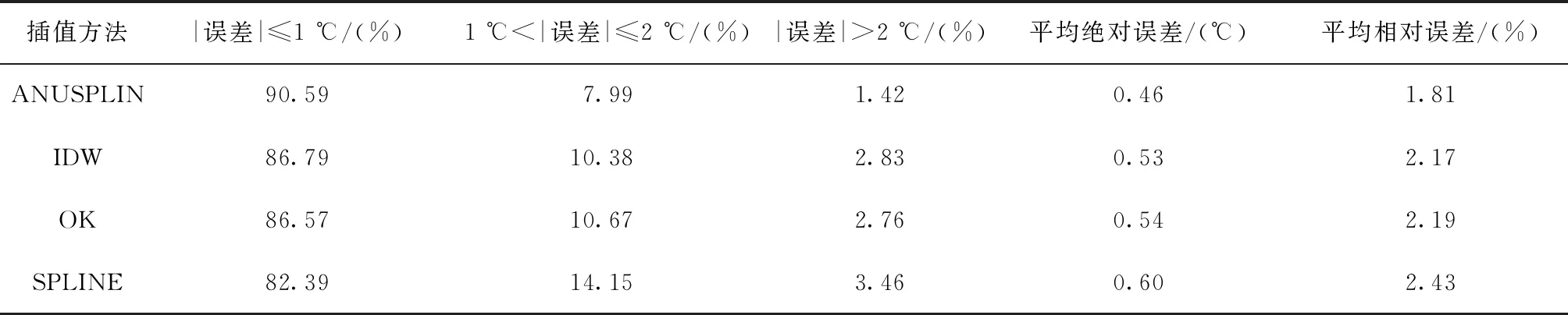
表2 误差参数分析

在气温插值误差空间分布方面，插值误差较大的站点分布在冀北高原燕山丘陵及太行山脉高海拔地区，而平原地区则误差较小，其原因可能是冀北高原燕山丘陵及太行山脉一带站点稀少且海拔较高，贾洋和崔鹏[11]的研究也证明ANUSPLIN插值精度主要受海拔影响，同时站点密度也是造成插值误差的原因之一[31]。

综上所述，4种插值方法在京津冀区域插值精度为ANUSPLIN>IDW>OK>SPLINE,基于ANUSPLIN软件的插值方法更加适合京津冀区域的逐日气温空间插值。

4 结论与讨论

本文使用京津冀区域以及临近省区2018年国家级及区域气象观测站日气温数据，采用ANUSPLIN研制京津冀区域逐日气温格点数据集，并与IDW、OK、SPLINE插值方法进行对比分析，得出以下结论：

1)基于4种插值方法对京津冀区域逐日气温数据进行插值的结果表明，ANUSPLIN插值结果与数字高程模型极为相似，插值效果优于IDW、OK、SPLINE，精度更高、光滑度更好。

2)通过计算预测值与实测值的相关系数(Corr)、MAE、MRE等作为检验插值精度的标准，4种插值方法得出的预测值与实测值相关性均较好，在站点密度足够高的前提下，各种插值方法用于同一组数据的插值结果差异不大，而插值误差则存在差异，综合评估，ANUSPLIN的插值结果最优，其次为IDW，再次为OK，基于SPLINE的气温插值结果最差，ANUSPLIN最适用于京津冀区域逐日气温插值。

3)京津冀区域逐日气温插值误差较大的站点分布在冀北高原、燕山丘陵及太行山脉一带，平原地区误差较小，海拔及站点密度是影响ANUSPLIN插值精度的因素之一。

综合分析，引入DEM的ANUSPLIN插值效果最优，但由于受模型本身的局限，本文只选择了经度、纬度和高程(m)三项作为自变量，没有考虑更多影响局地气温变化的因素，建议在后续的研究中，针对不同长度的时间序列、海拔、地形、DEM误差等因素开展更深入的研究。同时在验证插值精度时，仅采用了相关系数(Corr)、MAE、MRE几个误差指标进行简单验证，考虑到插值过程中会平滑掉一些极端值，在后续的研究中，应尽可能选取更多的误差指标及气温特征值进行验证，全面衡量插值精度。