超声检测方法研究HMX 及TATB 基PBX 的热循环性能

程 垄，徐 尧，李 丽，肖 盼，庞海燕，张伟斌

（1.中国工程物理研究院化工材料研究所，四川 绵阳621999；2.北京理工大学先进加工技术国防重点学科实验室，北京100081）

1 引言

高聚物黏结炸药（PBX）是由炸药晶体和高聚物黏结剂等组成的一种复合材料，反复变化的温度载荷作为热时效过程的工艺因素，以及贮存、运输和使用等过程的环境因素，将导致材料性能发生改变，直接影响到武器的使用性能和安全性能。

超声无损检测方法，具有非破坏、操作简单、效率高的优点，在国内外被广泛用于金属、复合材料、陶瓷等材料的性能表征，从不同角度来看，材料细观结构、形态以及相应的力学性能等很多方面能与超声时频参量、非线性参量等建立关系，使其成为材料性能表征的有效手段。在含能材料领域，田勇［1-4］、张伟斌［5-6］、韦兴文［7］、兰琼［8］、徐尧［9］等采用超声无损检测方法研究了压制成型、热处理、热循环、热冲击、机械载荷等过程对PBX 性能的影响，主要集中在利用分层、裂纹和疏松等内部缺陷的超声波信号进行内部质量的表征，利用超声波声速、增益和衰减量进行损伤破坏的表征，以及利用超声波声速进行应力状态的表征。在合金［10-11］、岩石［12-13］、混凝土［14-15］等材料领域，许多研究人员采用超声脉冲法测定了材料的声学参量、动弹性模量及泊松比，并开展其与力学性能、结构特征、微观机制的关系研究，但含能材料在环境温度反复变化下的性能及超声无损检测方法研究仍然有待开展探索性和适用性试验。

为了进一步探索超声无损检测方法在含能材料热循环性能研究中的适用性，对HMX 及TATB 基PBX 热循环试验过程中的超声纵、横波声速和动、静弹性模量等超声波特征参量变化规律进行了实验观察，并对这些超声波特性参量变化规律与热疲劳损伤和微裂隙、孔隙黏结剂流动等性能关系进行了分析讨论，为HMX及TATB 基PBX 热循环性能研究提供了新型超声无损检测方法支撑。

2 实验部分

2.1 试样

HMX 基PBX，中国工程物理研究院化工材料研究所；HMX 单质炸药晶体、F2311（氟树脂）黏结剂和部分钝感炸药TATB 组成的炸药造型粉经等静压压制大坯料，切取15 mm×102 mm 方哑铃平行试样（1#～10#），密度均为1.847 g·cm-3。

TATB 基PBX，中国工程物理研究院化工材料研究所；TATB单质炸药晶体和F2314（氟树脂）黏结剂组成的炸药造型粉经等静压压制大坯料，切取15 mm×102 mm方哑铃平行试样（11#～20#），密度均为1.893 g·cm-3。

2.2 仪器及试验条件

图1 动弹性模量测量系统Fig.1 Measurement system of dynamic elastic modulus

超声波传感器为2.25 MHz 横纵波一体化探头，中国工程物理研究院化工材料研究所自研；集合常规纵波直探头和常规横波直探头为一体，包括吸声材料、纵波压电晶片、横波压电晶片、阻尼块、电缆线以及外壳等，实现纵波和横波同时检测，保证纵波和横波垂直入射，耦合剂为Olympus 公司的SWC⁃2 横波耦合剂，如图2 所示。

利用ESPEC 公司生产的SETH⁃Z041U 调温调湿箱对HMX 及TATB 基PBX 试样进行热循环试验，在-40～75 ℃开展热循环试验。其中，室温—-40℃—75 ℃—室温为一个热循环试验周期，升降温速率为1 ℃·min-1，并 在-40 ℃和75 ℃恒 温2 h 使 试 样 温 度均匀稳定。HMX 基PBX 试样（1#～10#）和TATB 基PBX的10 个平行试样（11#～20#）分别经历3N 个（N=0，1，2，…，9）热循环试验周期。静弹性模量采用英国Instron 5582 万能材料试验机进行拉伸性能的测试，根据拉伸应力⁃应变曲线计算得到，测试参照GJB772A-1997 方法417.1 标准执行，横梁速度为0.5 mm·min-1，测试温度为（20±2）℃。

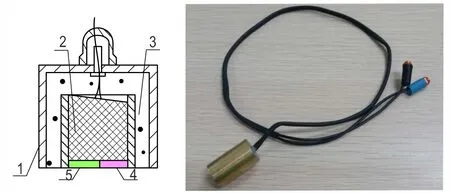
图2 横纵波一体化探头原理示意及实物图1—外壳，2—阻尼块，3—吸声材料，4—横波压电晶片，5—纵波压电晶片Fig.2 Schematic and physical diagram of integrated ultrason⁃ic longitudinal and transverse wave sensor1—shell，2—damping block，3—sound absorbing material，4—transverse wave piezoelectric wafer，5—longitudinal wave piezoelectric wafer

3 弹性模量和泊松比超声测量方法

动弹性模量（杨氏模量、剪切模量）和动泊松比采用超声声速法测量［17-18］。超声波在固体介质中的传播速度与介质的弹性模量和密度有关，通过测量介质中的纵、横波声速可计算得到其杨氏模量、剪切模量和泊松比。

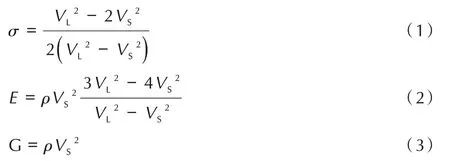
式中，E 为杨氏模量，GPa；G 为剪切模量，GPa；σ 为泊松 比；ρ 为 介 质 的 密 度，g·cm-3；VL为 纵 波 的 声 速，m·s-1；VS为横波的声速，m·s-1。

超声波纵波声速和横波声速通过厚度除以介质中传播声时的方法得到，计算公式为：

式中，h 为厚度，m；Δt 为声时，s；V 为声速，m·s-1。

4 试验结果与分析

4.1 超声声速-热疲劳损伤

HMX 及TATB 基PBX 经历不同热循环试验周期后的热循环试验周期⁃密度及超声参量关系见图3。

由图3a 可见，在试验过程中，随着热循环周期增加，HMX 基PBX 的密度降低且速率逐步平缓，TATB 基PBX 的密度呈先降低并速率放缓后略微回升的趋势。分析认为，热循环导致PBX 产生不可逆长大，密度降低，主要原因包括热膨胀系数不同导致黏结剂/炸药晶体界面脱粘引起塑性变形，内部微孔隙或微缺陷的扩张、炸药晶体的不可逆长大等。但随周期增加，密度降低速率放缓，甚至密度略微回升，这与热应力作用导致PBX 产生塑性形变的特性有关［7，19-20］。由图3b～图3f 可见，在试验过程中，随着热循环周期增加，HMX 及TATB 基PBX 的纵波声速、横波声速、动杨氏模量、动剪切模量的变化趋势与其密度变化趋势一致，动泊松比基本不变。

朱涛等[32]通过室内试验分析了宽级配砾质土的压实特性，结果表明，宽级配砾质土击实时干密度和含水率关系曲线呈上凸的抛物线型，具有一个最优含水率。击实后的最大干密度随着砾石含量的增加先迅速增大，后又开始逐渐减小。随着砾石含量的增加，其最优含水率先逐渐减小，后基本趋于稳定状态。

HMX 及TATB 基PBX 经历不同热循环试验周期后的纵波声速、横波声速⁃密度关系、线性拟合直线及拟合后线性关系表达式见图4。由图4 可见，在热循环试 验 过 程 中，HMX 和TATB 基PBX 的 纵、横 波 声 速 与密度具有正相关的线性关系。

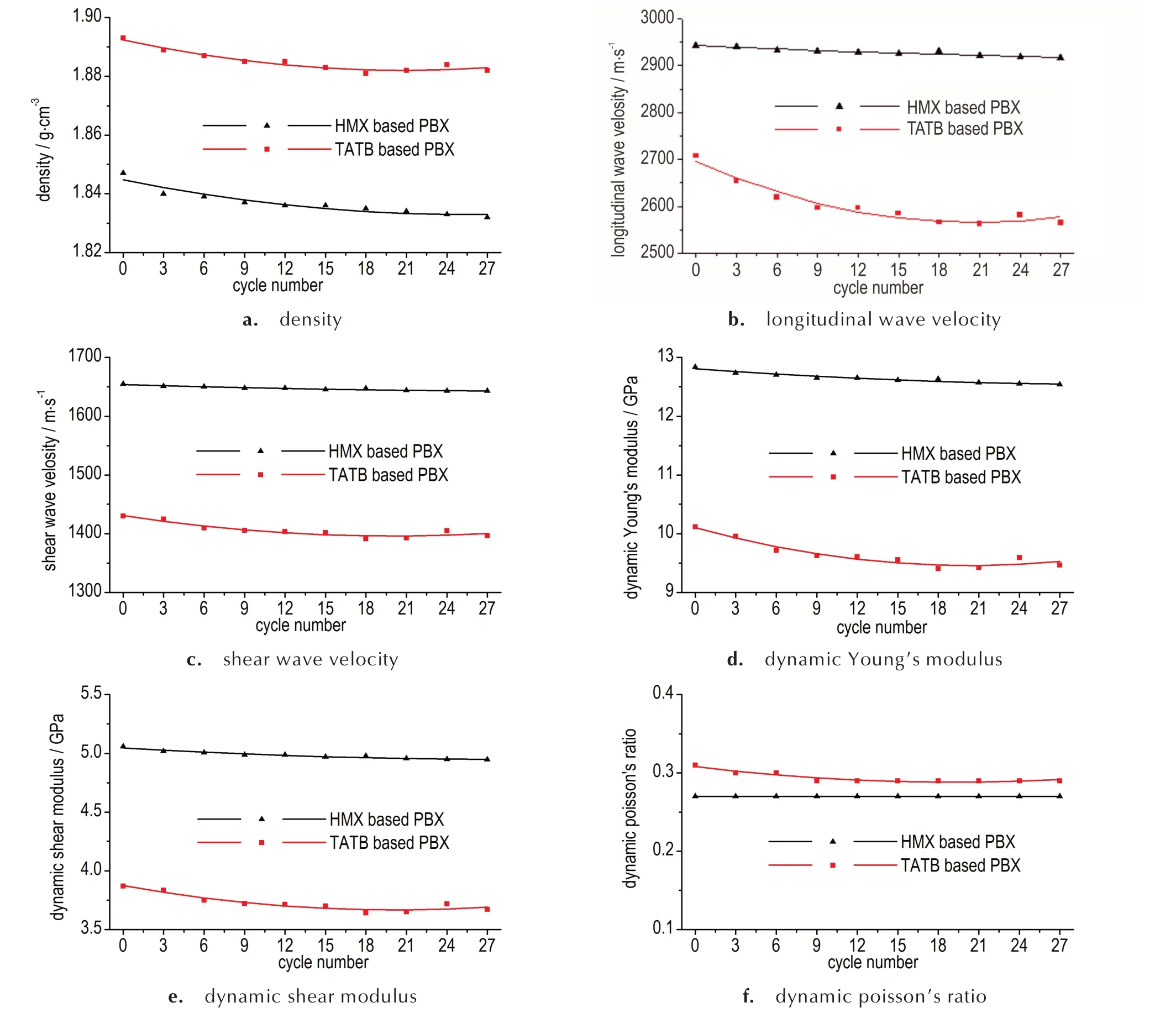
图3 HMX 及TATB 基PBX 的热循环试验周期⁃密度及超声参量关系Fig.3 The relationship between thermal cycle number and density and ultrasonic parameters of HMX⁃ and TATB⁃ based PBX

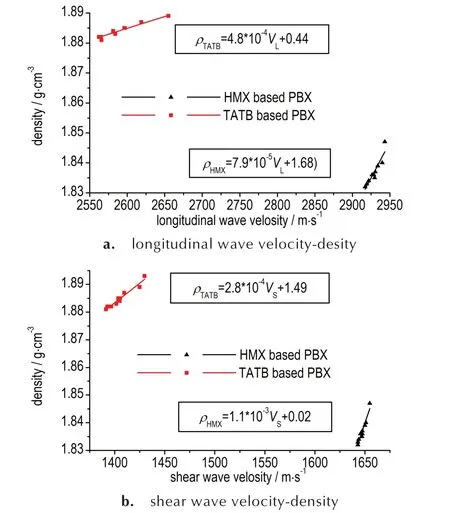
图4 热循环试验过程中HMX 及TATB 基PBX 纵波声速、横波声速⁃密度的线性关系Fig. 4 The linear relationship between longitudinal/shear wave velocity and density of HMX⁃ and TATB⁃ based PBX during thermal cycling

关联材料的整体微细观性能，热循环试验将使PBX 产生热疲劳损伤，基于Lemaitre［21］等效应变假设的损伤本构方程，损伤可通过损伤前后材料弹性模量的变化来定义或度量。

式 中，D 为PBX 的 损 伤 变 量；E 为 无 损PBX 弹 性 模 量，GPa；Ẽ 为受损PBX 弹性模量，GPa；ρ 为无损PBX 的密度，g·cm-3；ρ͂为受损PBX 的密度，g·cm-3；VL和VS分别为无损PBX 纵波声速，m·s-1；V͂L和V͂S分别为受损PBX纵波声速，m·s-1。

由式（2），（5），（6）和（7）可见，热循环试验过程中，PBX 热循环损伤量与密度变化和内部微损伤密切相关，可用密度和超声声速的表达式进行计算。如果PBX 密度已知，可利用式（2）和（5），通过超声纵、横波声速计算弹性模量，定量评价PBX 热循环试验中的热疲劳损伤；如果PBX 密度未知，可利用纵波声速或横波声速和密度的线性关系，将纵波声速或横波声速代入式（6）或式（7），直接通过纵波声速或横波声速定量评价PBX 热循环试验中的热疲劳损伤。

4.2 动静态模量⁃微裂隙、孔隙

HMX 及TATB 基PBX 经历不同热循环试验周期后的热循环试验周期⁃动弹性模量、静弹性模量和动静弹性模量比关系分别见图5 和图6。由图5 和图6 可见：（1）PBX 动弹性模量高于静弹性模量，动静弹性模量比大于1；（2）热循环试验过程中，HMX 及TATB 基PBX 都经历了静弹性模量先降低再升高，动静弹性模量比先升高再降低的两个阶段，前者拐点在第15 个热循环周期，后者拐点在第21 个热循环周期。

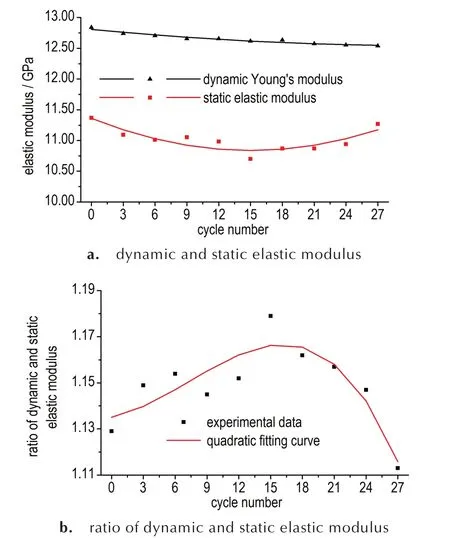
图5 HMX 基PBX 的热循环试验周期⁃动弹性模量、静弹性模量和动静弹性模量比关系Fig.5 The relationship between thermal cycle number and elastic modulus of HMX⁃based PBX

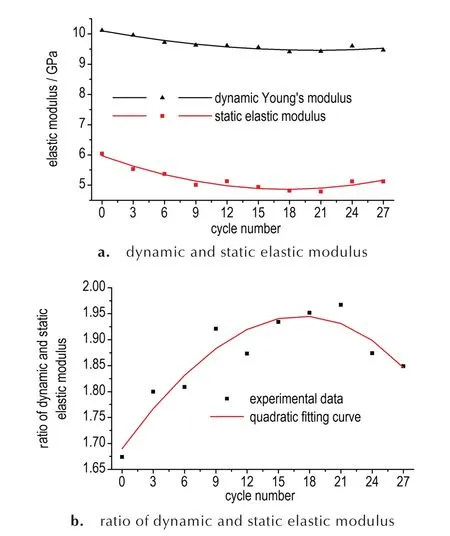
图6 TATB 基PBX 的热循环试验周期⁃动弹性模量、静弹性模量和动静弹性模量比关系Fig.6 The relationship between thermal cycle number and elastic modulus of TATB⁃based PBX

对其中微观作用机制进行分析讨论：

（1）动、静态载荷的应变幅值和载荷频率不同，静态属于无限低频率的大应变载荷，声波为小应变载荷。PBX 的动、静弹性模量之所以存在差异，是因为PBX 为多相不均匀介质，其内部和界面上通常存在较多的微孔隙、裂隙、裂纹等缺陷。在静态大应变条件下，PBX 将发生沿裂隙面或颗粒接触面的摩擦滑动，使PBX 静弹性模量降低。而声波引起的应变很小，不足以引起这种滑动，因而PBX 动弹性模量高于静弹性模量。

（2）PBX 是由炸药晶体和高分子黏结剂所组成的复合体系，热循环试验过程中有类似岩石弹性物理研究中的岩石骨架和孔隙流体的结构特性。参考Gassmann 方程理论［22］及其在岩石孔隙弹性特性［23］和动态与静态弹性参数差别中的应用研究［24］，从材料内部因素出发，可知静弹性模量受微裂隙（裂隙面或颗粒接触面）影响，微裂隙增加，静态大应变条件下更容易摩擦滑动，则静弹性模量降低；反之，则相反。而小应变声波加载对微裂隙不敏感，动弹性模量受微孔隙流体粘度，主要是高聚物黏结剂的粘弹态甚至流态变化的影响。

（3）对热循环试验中PBX 动、静弹性模量和动静弹性模量比变化的物理机理初步解释为：热循环试验第一个阶段是PBX 尺寸不可逆长大，加上黏结剂和炸药晶体热膨胀系数不一致，造成的颗粒边界微裂隙增加，微裂隙率增加，使PBX 静弹性模量降低；第二个阶段由于热循环试验，特别是高温段的反复作用下，PBX中玻璃化温度较低（30 ℃左右）的黏结剂以及少量低熔点助剂变成粘弹态甚至流态［4］，一方面，使得PBX 各组分之间特别是黏结剂与炸药晶体之间原本不太好的界面状态得到改善，静弹性模量升高；另一方面，微孔隙中粘弹态甚至流态黏结剂的存在为动态测试下的炸药提供了附加刚度使动弹性模量降低速率减缓。

5 结论

（1）在热循环试验过程中，随着热循环周期增加，HMX 基PBX 的密度降低且速率逐步平缓，TATB 基PBX 的密度呈先降低并速率放缓后略微回升的趋势。纵波声速、横波声速、动杨氏模量、动剪切模量的变化趋势与其密度变化趋势一致，动泊松比基本不变。

（2）热循环损伤量与密度变化和内部微损伤密切相关，可用密度和超声声速的表达式进行计算，且热循环试验过程中纵、横波声速与密度具有正相关的线性关系，因此超声纵波声速或横波声速可直接定量评价PBX 热循环试验中的热疲劳损伤。

（3）PBX 动弹性模量高于静弹性模量，动静弹性模量比大于1，差别是因为PBX 为多相不均匀介质，且其内部和界面上通常存在较多的微孔隙、裂隙、裂纹等缺陷的结构特征，导致动、静态载荷加载效果不同。

（4）在热循环试验过程中，随着周期增加，HMX及TATB 基PBX 的静弹性模量先降低再升高，动静弹性模量比先升高再降低，前者拐点在第15 个热循环周期，后者拐点在第21 个热循环周期，内在因素包括第一阶段的微裂隙率增加和第二阶段的微孔隙中粘弹态甚至流态黏结剂。