基于Dice系数的变步长自适应匹配追踪算法
张世强,马 可,张婷娟,黄 雷,宋人杰
(1.国网黑龙江省电力有限公司 伊春供电公司,黑龙江 伊春153000; 2.东北电力大学 计算机学院,吉林 吉林132012)
0 引 言
在信号处理领域中,传统的信号处理方法为奈奎斯特采样定理,即当采样频率为信号频率的2倍时,该信号可以进行无失真的采样。但是社会对于信号的带宽需求越来越大,如果继续利用奈奎斯特采样定理进行信号处理,对于信号处理的物理硬件的研究会变得昂贵且复杂,而压缩感知(Compressed Sensing,CS)[1]的出现很好地解决了这个问题。压缩感知理论可以使信号在远低于奈奎斯特采样定理要求的采样频率下对信号进行采样,并且几乎无失真地重构出原信号。因此压缩感知也成为当下的研究热点,用于电能信号[2-3]传输等研究。
压缩感知理论主要分为3部分:第1部分为信号的稀疏化,压缩感知要求信号必须具有稀疏性,所谓稀疏性是指信号中大部分成分为0或趋近于0,只有小部分含有信号信息。但是自然界中的信号大多不是稀疏信号,因此要对信号进行稀疏处理,信号的稀疏化是压缩感知理论的前提;第2部分为测量矩阵的设计,信号通过测量矩阵,就是对信号进行压缩和采样。测量矩阵的维度就是信号压缩后的维度,对测量矩阵的要求是在压缩矩阵的同时不能丢失信号的重要信息;第3部分为信号重构,目的是将压缩后的信号无失真地恢复出来,在信号传输的过程中,信号重构是最为重要的一部分,重构算法的好坏直接决定了压缩感知能否应用于实践。
在重构算法中,贪婪算法因其算法结构简单且重构性能较好的特点而广泛应用在实际中。其中正交匹配追踪(Orthogonal Match Pursuit,OMP)算法[4]是贪婪算法中最基础的算法,该算法利用每次迭代挑选测量矩阵与信号残差最相关的原子,用最小二乘法求出最优解,进而求出重构信号。在OMP的基础上,研究人员相继提出了正则化匹配追踪(Regularization OMP,ROMP)算法[5],广义正交匹配追踪(Generalized OMP,GOMP)算法[6]以及压缩采样匹配追踪(Compression Sample Match Pursuit,CoSaMP)算法[7]。此类算法均有较高的信号重构精度,但是都有相同的缺点,即算法必须要在已知信号稀疏度的条件下进行,但是在实际应用中,大多数信号的稀疏度都是未知的,因此此类算法并没有较高的应用能力。针对这个问题,T. Thong提出了稀疏度自适应匹配追踪(Sparsity Adaptative Match Pursuit,SAMP)算法[8],该算法设定1个估计稀疏度值和步长,然后通过步长使每次迭代中估计稀疏度都扩充步长大小,直至估计稀疏度与真实稀疏度相似或相等时,利用扩充集中的原子进行估计信号的计算。因此该算法可以在未知稀疏度的条件下对信号进行重构,拥有较为广泛的应用前景。
但是SAMP算法仍存在一定缺陷,因为该算法使用固定步长估计稀疏度,因此对固定步长比较依赖,当步长设定较大时,在迭代后期会出现稀疏度过估计的情况,进而影响算法的重构性能。当步长设定较小时,则会增加算法的迭代次数,增加算法的运行时间,降低了SAMP算法的应用能力。针对这个问题,提出利用残差控制步长的方式,将信号残差分为2个区间,当残差处在不同区间时,改变步长使估计稀疏度值可以逐步贴近真实稀疏度,减小稀疏度过估计的可能。同时,利用广义Dice系数代替SAMP算法中的内积法求取原子相关性,使求出的相关性更加准确。
1 压缩感知理论框架
压缩感知的本质是信号经过测量矩阵后实现信号维度降低的过程,如式(1)所示。
y=Φx
(1)
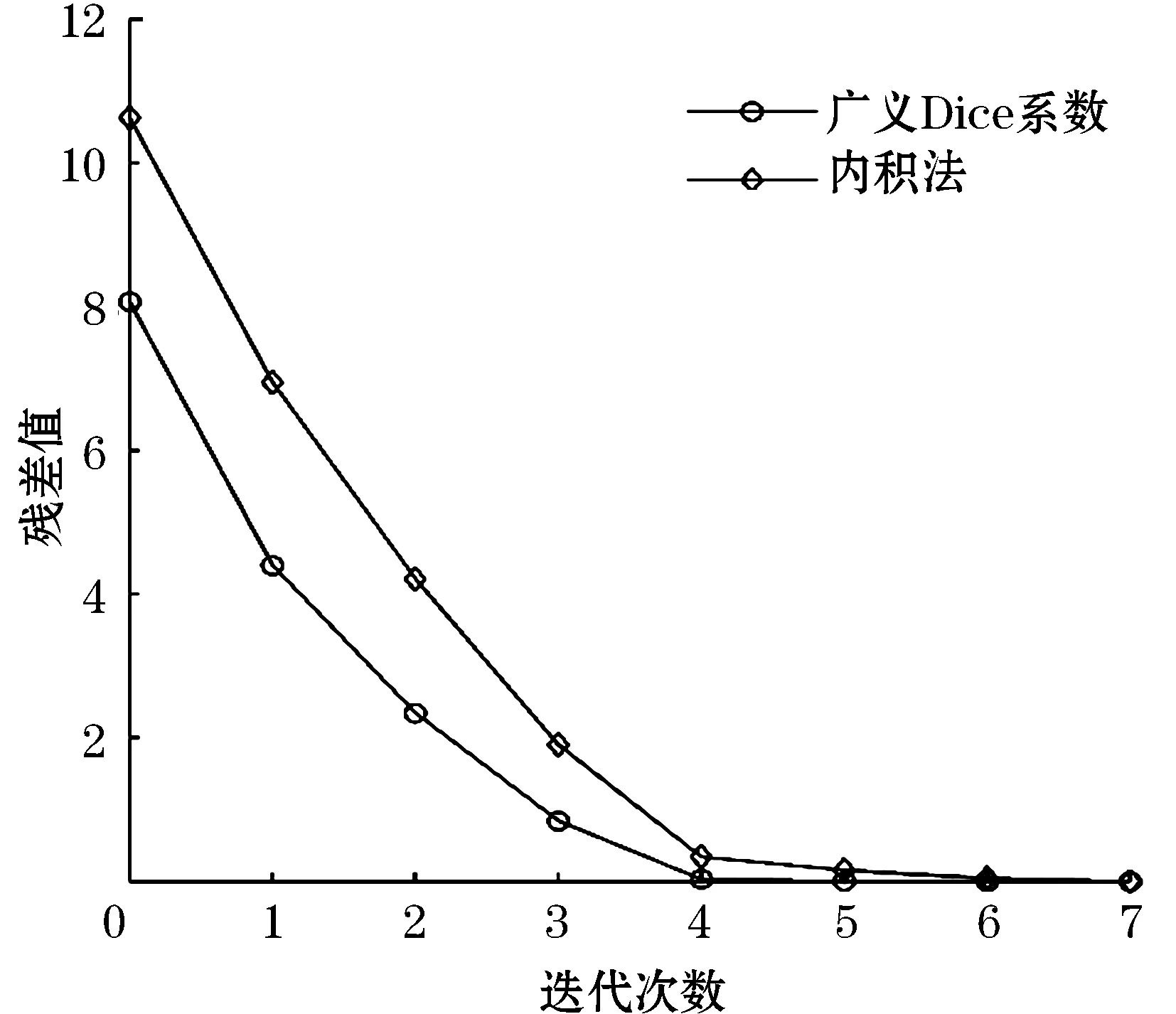
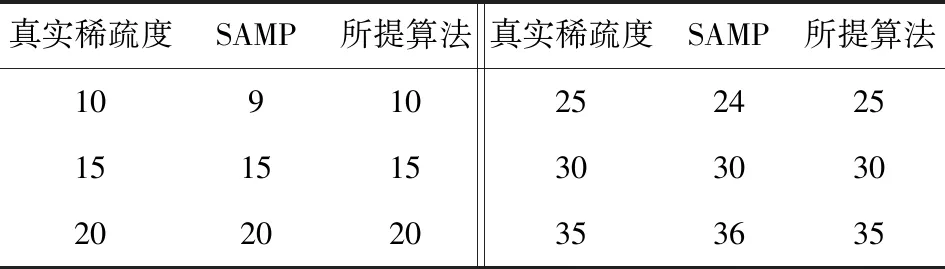
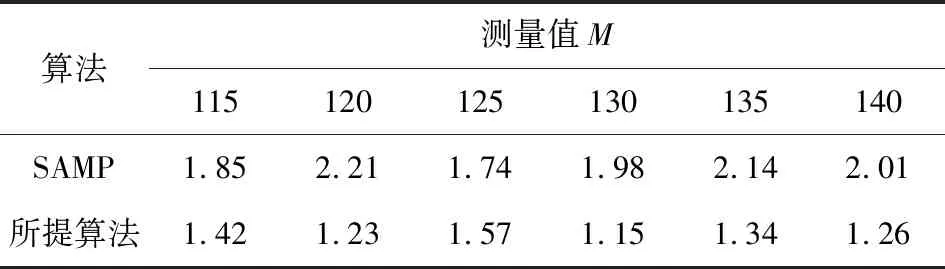
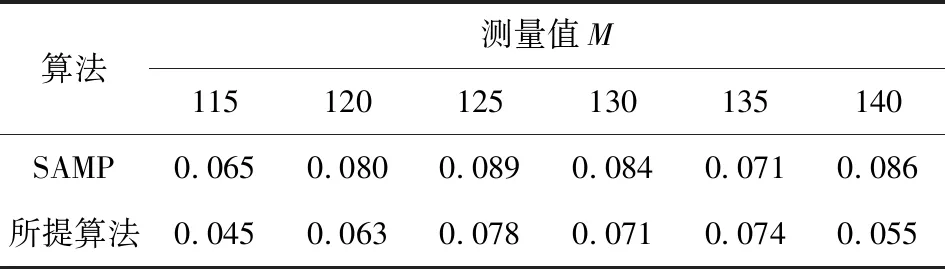
式中:x为N×1维的信号;Φ为M×N的测量矩阵。其中M 当原信号x不是稀疏信号时,需要将信号先进行稀疏化使其变为稀疏信号,如式(2)所示。 x=Ψα (2) 式中:α代表稀疏化的信号,如果α中包含K个非0元素(K=N),或者说α中包含K个数值较大的元素,剩下的元素趋近于0。就证明经过α信号是原信号x通过稀疏基Ψ变换而来的K稀疏信号。 结合式(1)与式(2),可以得出压缩感知理论的通用方法如式(3)所示。 y=Φx=ΦΨα=Aα (3) 式中:A=ΦΨ称为感知矩阵。 在得到了压缩后的信号y后,就可以利用信号重构算法,将y恢复成原信号x,如式(4)所示。 (4) 其中,x为N维且y为M维,因此有x个未知数求y个解,这本质上是一个NP-hard问题,针对这一问题,研究人员大多用基于l0范数的贪婪算法解决。 SAMP算法是重构算法中应用最广泛的算法,因为该算法可以在未知稀疏度的条件下进行对信号的重构。SAMP算法在迭代初始阶段设定1个阶段数Stage=1以及步长s,并在开始时将估计稀疏度值设定为1,每次迭代通过阶段数控制估计稀疏度值的增长,如式(5)、(6)所示。 Stagek=Stagek-1+1 (5) Lk=Stagek×s (6) 式中:Lk为估计稀疏度值;Stagek为迭代次数。 从式(5)和式(6)可以看出,在每次迭代中估计稀疏度值都增加一个步长大小,直到估计稀疏度值与真实稀疏度值相近时,将信号重构出来。SAMP具体步骤如图1所示。 由SAMP的算法步骤可以看出,该算法十分依赖步长的大小,如果步长选择过大,则会出现稀疏度过估计的情况,影响算法重构结果。为了使估计稀疏度更精确,可以让步长为1,逐步地增加稀疏度,但这样也会加大算法的迭代次数,导致算法运行时间加长,降低了SAMP算法的实际应用能力。 输入:M×N的感知矩阵A=ΦΨ,M×1的测量值y,初始步长s,停止阈值η,阶段数Stage0=1初始化:初始残差r0=y,支撑集∧0=Ø,候选集C0=Ø,初始稀疏度估计值L0=s,迭代次数k=11)计算原子相关度u=〈rk-1,A〉,并将前Lk个最大值的列序号加入集合Sk中2)得到支撑集∧k=∧k-1∪Sk3)利用最小二乘法求信号估计值^x∧k=A+∧k·y与残差 rk-1=y-A∧k·^x∧k4)回溯:在x∧k中选择Lk个最大值,将这些值对应的列序号记录下来并加入集合F中5)利用F中的原子信息再次求取信号估计值^xF=A+F·y与残差rnew=y-AF·^xF6)当rnew2≥rk-12时,Stagek=Stagek-1+1,Lk=Stagek×s,k=k+1返回步骤1),如果不满足条件,rnew=rk-1,∧k=F,k=k+1返回步骤4)。7)当触发rn2<η时,停止迭代,输出重构所得信号估计值^x∧k输出:信号x的近似估计值^x 针对SAMP算法出现的不足,在2个方面做出改进。在贪婪算法中,重构信号的质量在于每次迭代选择测量矩阵与信号残差中相关原子的准确性,挑选的原子相关性越高,重构效果越好。但是在SAMP算法中是由内积法进行相关性的计算的。内积法就是求2个向量的夹角余弦值,余弦值越大代表2个向量越相似。内积法本质如式(7)所示,可以看到内积法中分母采用的是几何平均数,根据平均值理论,几何平均值的重点在于表现样本总体变化趋势,无法突出样本中重要信息,因此在匹配过程中会有丢失部分原子信息的情况发生[9],导致相关性计算不准确,进而影响重构结果。 (7) 针对这一问题,提出利用广义Dice系数替换内积法来计算原子相关性。式(8)中展示了广义Dice系数的本质,可以看出分子部分与内积法相同,但在分母中广义Dice系数利用算术平均值代替几何平均值。在平均值理论中,算术平均值代表样本个体期望的无偏估计,因此能更好地保留原子信息。 (8) 图2为不同相关性计算方法的结果对比,将2种计算原子相关性的方法带入到基础的SAMP算法中,除了相关性计算方法不同,其他的条件完全一致。 图2 不同相关度所计算出的残差 由图2可以看出,使用广义Dice系数的重构算法的残差更快地趋近于0,证明广义Dice系数计算的相关性更加精确。因此,在改进算法中用广义Dice系数D〈x,y〉代替内积法进行原子相关性的计算。 sk=「0.5×sk-1⎤ (9) Lk=Lk-1+sk (10) 式中:s为步长;L为估计稀疏度值;「⎤为向上取整。 由式(9)可知,当残差值处于第二区间时,步长在每次迭代中减小一半,并按照向上取整处理。这样可以使步长迅速衰减为1,通过式(10)来计算估计稀疏度,可以看出步长越小,估计稀疏度增长越慢,因此在迭代后期步长减少至1时,可以逐步增加估计稀疏度值,减少稀疏度过估计的可能性。改进算法针对SAMP算法做出两步改进,具体步骤如图3所示。 输入:M×N的感知矩阵A=ΦΨ,M×1的测量值y,初始步长S0,残差阈值η1,η2,阶段数Stage0=1初始化:初始残差r0=y,支撑集∧0=Ø,候选集C0=Ø,初始稀疏度估计值L0=s,迭代次数k=11)计算原子相关度u=D〈rk-1,A〉,并将前Lk个最大值的列序号加入集合Sk中2)得到支撑集∧k=∧k-1∪Sk3)利用最小二乘法求信号估计值^x∧k=A+∧k·y与残差 rk-1=y-A∧k·^x∧k4)回溯:在x∧k中选择Lk个最大值,将这些值对应的列序号记录下来并加入集合F中5)利用F中的原子信息再次求取信号估计值^xF=A+F·y与残差rnew=y-AF·^xF6)当残差rnew2≥η1时,如果rnew2≥rk-12,Stagek=Stagek-1+1,Lk=Stagek×s,k=k+1返回步骤1),如果不满足条件,rnew=rk-1,∧k=F,k=k+1返回步骤4)。7)当η1>rnew2>η2时如果rnew2≥rk-1,sk=「0.5×sk-1⌉,Lk=Lk-1×sk,k=k+1返回步骤1),如果不满足条件,rnew=rk-1,∧k=F,k=k+1返回步骤4)。8)当rn2<η2时,停止迭代,输出重构所得信号估计值^x∧k输出:信号x的近似估计值^x 针对所提SAMP的改进算法进行仿真,来验证其重构性能。采用长度为256的高斯随机稀疏信号作为原始信号,测量矩阵为随机产生且服从高斯分布的矩阵。所得实验数据均是在4核Matlab2014b的条件下进行500次所取的平均值。 表1为2种算法估计稀疏度与真实稀疏度的差距,为了体现出固定步长的不足,仿真选取步长为3,测量数M=128。所提算法中残差阈值分别为η1=10-2,η2=-10-6,SAMP的停止阈值设为10-6。可以看出,SAMP算法中估计稀疏度值受限于步长,只能做到贴近真实稀疏度,会出现稀疏度过估计或估计不足的情况。但是所提算法由于迭代后期改变了步长,因此可以做到与真实稀疏度相等,具有较好的重构结果。 表1 估计稀疏度与真实稀疏度的比较Table 1 Comparison between real sparsity and estimated sparsity 表2记录了所提算法与SAMP算法的平均重构误差对比。仿真选取测量值M∈[115,140],K=30。其他实验条件与上一个实验条件相同。可以看出,由于使用了变步长的策略以及广义Dice系数,因此所提算法的重构误差要远小于SAMP算法。证明了所提算法在多频带信号重构上有着更高的重构精度。 表2 算法在不同测量值下误差的比较Table 2 Error comparison of two algorithms under different measured values (×10-14) 表3比较了2种算法的平均运行时间,虽然所提算法使用了变步长的策略,后期步长减小会增加迭代次数,但是由于使用了广义Dice系数计算原子相关度,因此在原子的选择上更加精确,可以使算法更快地收敛,因此所提算法的运行速度比SAMP算法高出10%~20%。基于表2和表3可以得出,在一维信号的重构表现上,所提算法拥有更好的重构性能。 表3 算法在不同测量值下运行时间的比较Table 3 Comparison of running time of algorithm under different measured values s 在验证了所提算法在一维信号中有较好的重构性能后,用二维图像信号验证所提算法的普适性,图4为所提算法与SAMP算法对二维图像的重构结果。 图像采用256×256的2张实际电厂图像[10-11]作为二维信号,稀疏基采用小波稀疏基,仿真中用峰值信噪比(Peak Signalto Noise Ratio,PSNR)来表示重构的精度,PSNR值越高代表重构效果越好。测量值M=128,所提算法与SAMP算法的步长均为3。图4表示所提算法与SAMP算法对图像信号的重构结果,可以看出所提算法的PSNR值相比SAMP算法要高2 dB左右,证明所提算法在图片的细节上重构得更加精细,重构效果更好。 针对SAMP算法中固定步长会影响估计稀疏度值计算的问题。采取了2种改进方案: 1)用广义Dice系数代替原有的内积法,使计算出的原子相关性更准确。 2)利用残差控制步长,当残差值处于一定区间时,逐步减小步长,减少稀疏度过估计的情况。 利用一维信号与二维信号的仿真实验证明所提算法具有良好的重构性能。2 SAMP算法

3 改进SAMP算法
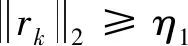

4 仿真实验
5 结 语

