椭圆(双曲线)焦点三角形中的一个不等式

广州市禺山高级中学(511483) 蓝贤光

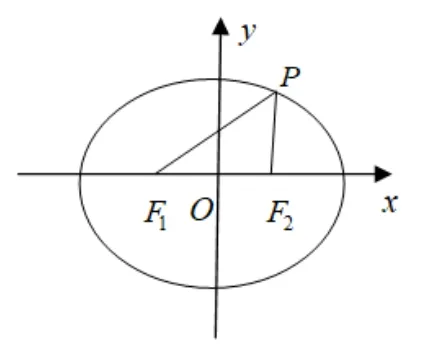
在高三的一次综合训练中有这样一道填空题:

题目1设P是椭圆+y2=1 上异于长轴端点的任意一点，F1，F2是该椭圆的两个焦点，∠F1PF2=60◦，R，r是ΔPF1F2的外接圆和内切圆半径，则=____.

解析显然a=2，b=1，c=在ΔPF1F2中由正弦定理得

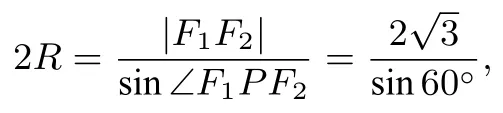
即R=2;又

且

经探究，我们有以下的

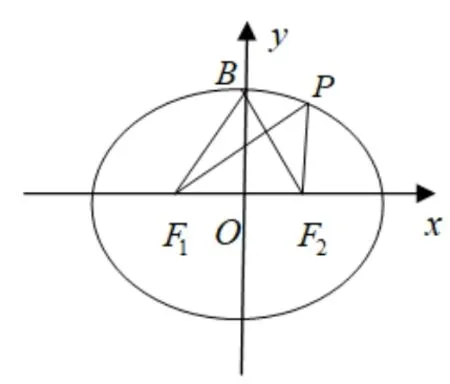
性质1设P是椭圆=1(a ＞b ＞0)上异于长轴端点的任意一点，F1，F2是该椭圆的两个焦点，e是该椭圆的离心率，∠F1PF2=2θ，R，r是ΔPF1F2的外接圆和内切圆半径，则

证明在 ΔPF1F2中由正弦定理得 2R=即又b2·tanθ，且

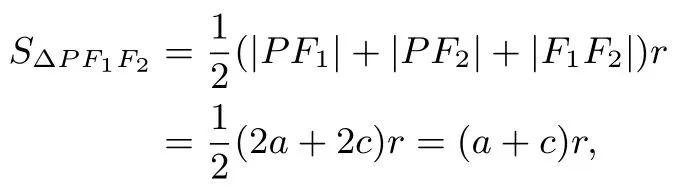
所以(a+c)r=b2tanθ，r==(a-c)tanθ，从而

设B是该椭 圆短轴的 一 个端点，∠OBF1=α，则0＜θ≤α ＜，sⅰnθ≤sⅰnα=，于是

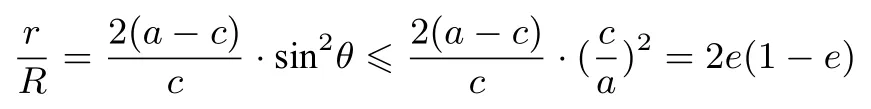
当且仅当sⅰnθ=sⅰnα=，即点P与点B重合时“=”成立，证毕!

将上述性质类比到双曲线上去，我们又有以下的

性质2设P是双曲线=1(a ＞0,b ＞0)上异于实轴端点的任意一点，F1，F2是 该双曲线的两个焦点，e是该双曲线的离心率，∠F1PF2=2θ，R，r是ΔPF1F2的外接圆和内切圆半径，则

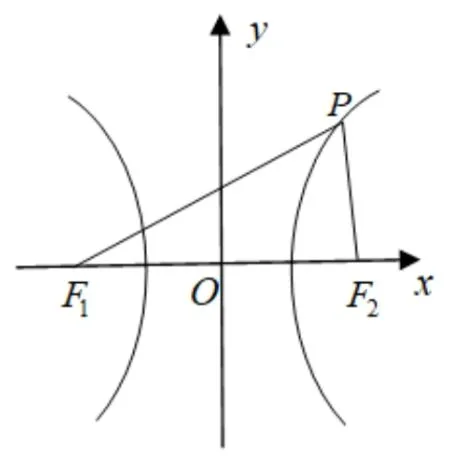
证明在 ΔPF1F2中由正弦定理得 2R=且

在ΔPF1F2中由余弦定理得:

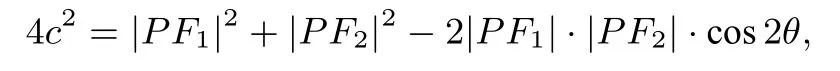
所以4c2=(|PF1|-|PF2|)2+2|PF1|·|PF2|·(1-cos 2θ)

或4c2=(|PF1|+|PF2|)2-2|PF1|·|PF2|·(1+cos 2θ),

于是，

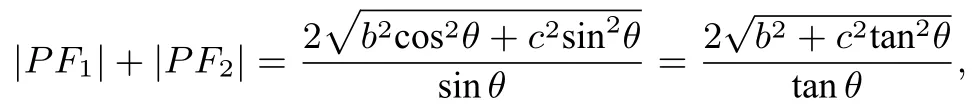
所以

从而

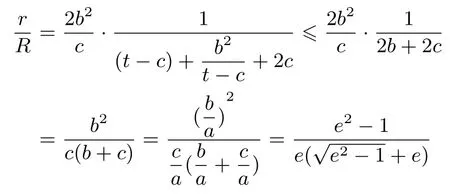
当且仅当tanθ=时等号成立，此时可求得点P的坐标为