利用记忆单元改进DQN的Web服务组合优化方法

杨 波 胡国兵

1(南京信息职业技术学院信息服务学院 江苏 南京 210023) 2(金陵科技学院电子信息工程学院 江苏 南京 211169)

0 引 言

随着网络技术的发展，面向复杂环境的服务组合在现实生活中的应用越来越多，而面向复杂环境的Web服务组合的进一步应用会面临难以优化的问题。面向服务计算(Service-Oriented Computing,SOC)的基本目标是实现在各种平台上运行的不同软件和数据应用程序之间的互操作性[1]。因此只有当存在众多服务提供商和服务消费者彼此协作时，才能发挥SOC的全部潜力[2]。由于面向服务的环境中固有的动态性和复杂性，良好的服务组合解决方案需要适应这些动态服务环境的变化和波动。此外，功能等同服务数量的爆炸性增长迫切需要能够处理此类任务的有效服务组合算法[3-4]。由于一个服务不能满足所有用户要求，因此需要将组件服务转换成组合服务。在这方面，服务组合成为实现面向服务的体系结构(System of Archtecture，SOA)的最有效技术。

为了对面向复杂环境的Web服务组合进行优化，学者进行了大量的研究，在复杂环境下，从大量的满足功能需求但是非功能需求的Web服务中，选择出满足用户需求的组合服务所采取的服务选择策略可以有多种，研究文献可主要分为三种：群智能算法、人工智能(Artificial Intelligence，AI)方法和其他混合方法。群智能算法如文献[5]提出的多目标服务组合优化推荐方法(Multi-Objective Service Combination Optimization Recommendation Method，MO-SCORM)，具有较好的可适应性和自组织性，通过将细粒度的Web服务粗粒化实现了面向个性化客户的体系结构，其协作性和健壮性较好，但效率较低；文献[6]从功能等同的具体服务集合中选择了满足消费者强加的服务质量(Quality of Service，QoS)，对最佳服务集合进行约束，提高了服务组合的服务质量，但在服务效率方面还需进一步提高。在大数据背景下为改善算法效率，智能算法得到了广泛应用：文献[7]提出了一种结合顺序决策过程的强化学习方法(Sequential Decision-Making Process-Reinforce Learning，SDMP-RL)并将其应用在Web服务组合的优化问题中，使代理与环境交互，通过反复实验提高了Web组合服务的学习最优解，但该方法在面对可扩展性的服务环境时表现较差；文献[8]采用深度Q学习(Deep Q-Learning，DQL)解决了Web服务组合效率低的问题，但是没能兼顾Web组合服务对复杂环境的适用性和可扩展性。现有的Web服务组合方法在面对复杂的服务环境时，难以同时在服务环境的适应性、可扩展性和动态性这几个指标上获得良好的综合性能。针对面向高可扩展性、复杂性和异构性服务环境的Web服务组合难以进行优化的问题，本文提出一种利用记忆单元改进DQN的Web服务组合优化方法。其创新点主要体现为以下两点：

(1) 引入LSTM-DQN方法进行优化，提升了DQN算法的全局寻优能力；

(2) 利用强化学习的组合优化模型简化组合优化过程，并将LSTM-DQN方法应用于Web服务组合优化问题，提升了Web服务组合的处理效率。

1 基于Markov的组合优化模型

组合优化模型采用马尔可夫决策过程MDP作为一般方案，以描述动态环境中的服务组合和适应过程。MDP是离散时间随机控制过程，用于对不确定域中的顺序决策进行建模。MDP的关键组成部分正式定义如下[9]：

定义1Markov 决策过程(MDP)。一个MDP可以定义为一个五元组MDP=，其中：S是一组有限状态；A(s)是一个有限的动作集合，取决于当前状态s∈S;P是一个概率值，也就是当动作a∈A被执行时，发生一个从当前状态s到结果状态s′的一个状态转移，其转移概率分布为P(s′|s,a)；R是奖励函数。类似地，当执行操作a时，从状态s转移到s′，将收到一个实际值的奖励r，其预期值为r=E(R(s′|s,a))；γ∈[0,1]是区分未来奖励和即时奖励重要性的折扣因素。

MDP的解决方案是一个决策策略，通常决策策略π是从状态到操作的概率分布的映射，定义为π:S→A如果MDP是偶发性的，即状态在长度t的每一场景后重置，则一个场景中的状态、行动和奖励序列构成策略的轨迹或推出[10]。策略的每个推出都会从环境中累积一个奖励，从而返回R。解决方案中算法的目标是找到一个最佳策略，该策略累积了所有状态的最大预期回报。

2 基于强化学习的组合优化模型

RL的目的是设计算法，通过这些算法，代理可以学习在某些环境中的自主操作，从他们与该环境的交互或从环境中收集的观测值中学习。此环境通常作为MDP制定。与传统的动态编程技术不同，强化学习算法不需要有关MDP的知识，它们针对的是精确方法变得不可行的大型MMDP。在此背景下，RL旨在根据它们与环境的交互来确定最佳控制策略[11]。此策略可以通过基于一组四元组(st,at,rt,st+1)近似所谓的Q函数来实现。其中：st表示t时刻的环境状态；at表示所执行的控制操作；rt表示所获得的瞬时奖励；st+1表示环境的后续状态，并通过Q函数决定控制策略。

最适合RL的问题类型是复杂的控制问题，其中似乎没有明显或易于编程的解决方案。因此，在开放和动态环境中使用RL进行自适应服务组合具有明显的优势。通过在组合模型中使用RL，它可以以自适应的方法学习最佳服务选择策略[11]。基于MDP的动态服务组合中使用的关键概念定义如下：

奖励值r可以使用操作值函数计算：

Qi(s,a)←Qi(s,a)+α[r+γmaxa′Qi(s′,a′)-

Qi(s,a)]

(1)

式中：s表示状态空间(即抽象服务)，表示代理i遍历所有可能的工作流时全部状态的集合；α是学习率，它控制收敛；当代理i选择一个Web服务ws时，代理i收到一个奖励，这是一个聚合值的QoS的ws属性。此奖励值可以根据下式计算：

(2)

在此模型中，采用ε-贪婪策略，使学习代理能够在选择过去尝试过的Web服务(即利用)和随机选择可能提供更好的结果的新Web服务之间进行权衡(即探索)。对于代理i，给定状态和一组可用的Web服务Ai(s)，代理i选择下一个 Web 服务j的概率为：

(3)

式中：ε是单个 Web 服务的概率分布,[·]表示对中括号内的内容进行记分。代理i根据ε-贪婪策略的概率(1-ε)选择最佳的Web服务，否则以概率ε选择一个统一随机的Web服务[12]。

3 LSTM-DQN的Web服务组合优化方法

3.1 深度Q神经网络算法

深度Q神经网络(Deep Q-Network，DQN)是基于深度学习和强化学习思想而提出的无监督学习方法。在高维度状态或动作空间中，深度强化学习存在难以估计每个大型状态和操作空间所对应的Q值问题。为了解决该问题，引入了深度Q神经网络，使深度强化学习代理的各个组成部分利用梯度下降对参数进行训练，以尽量减少一些不必要的损失函数[13]。DQN算法原理如图1所示。

图1 DQN算法原理

在深度学习计算Q值的过程中，DQN 算法通过权重为θ的神经网络近似器来估计Q值，该神经网络的输入为状态，经过卷积、池化、全连接等操作，输出该状态下每个动作的Q的估计值。智能体的目标是找到一种未来反馈值最大的动作选择方式，利用该动作选择方式与环境进行交互。因此定义最优动作选择函数为Q(s,a)，其算式为[14]：

(4)

式中：s为状态；a为该状态下执行的动作；π为动作和状态映射；st为t时间步时的状态；at为st状态下执行的动作；Rt为状态时s执行动作a得到的反馈值；T为总时间步；t′为求和过程变量；rt为第t个时间步的反馈值[15]。

综上所述，根据深度学习和强化学习计算的Q值，通过对损失函数Le(θe)使用梯度下降法更新权重θ，来优化 Q神经网络：

Le(θe)=Es,a～p(·)[(ye-Q(s,a;θe))2]ye=Es′[r+γmaxa′Qe(s′,a′;θe)|s,a]

(5)

式中：Q(s,a;θe)为Q(s,a)的估计值；e为迭代次数；s为当前状态；a为当前动作；s′为下一个状态；a′为下一个动作；p(s,a)为状态s和动作a的概率分布。

3.2 LSTM改进的深度Q神经网络算法

为了在大型服务环境中启用自适应服务组合，提出一种基于改进DQN的模型，该模型包括生成器φR和动作记分器φA，模型的整体架构如图2所示。

图2 改进DQN模型框架

为了更好地描述模型，采用长-短期记忆网络(Long Short-Term Memory Network，LSTM)表示生成器。LSTM是递归神经网络，能够连接和识别输入向量之间的长程模式，在一定程度上可捕捉潜在信息。所提模型中，LSTM网络将输入向量嵌入潜在因子wk，并在每个步骤生成输出向量xk。为了得到最终的状态vs，添加了一个平均池层，用于计算输出向量xk上的元素平均值[16]：

(6)

生成器的输出向量作为动作记分器的输入，即vs=φR(s),输出是所有动作的分数。同时预测所有动作的分数，这比分别对每个状态动作进行分数计算更有效。通过生成器和动作记分器，可得到Q函数的近似值Q(s,a)≈φA(φR(s))[a]。

由于计算上的限制，所提LSTM-DQN方法将命令视为由一个操作和一个参数对象组成[17]。考虑到所有可能的动作和对象，使用同一个网络对每个状态进行预测。该法使用随机梯度下降和RMSprop学习表示生成器的参数r和动作记分器的参数a，完整的训练过程如算法1所示。在每次迭代e中，更新参数以减少当前状态Q(st,at;θe)(θe=[θR;θA]e)的预测值与给定奖励rt的预期q值和下一状态maxaQ(st+1,a;θe-1)的值之间的差异[18]。

▽θeQ(s,a;θe)]

(7)

式中：▽θe表示对θe求导。

算法1LSTM-DQN训练程序

1. 输入经验记忆D

2. 初始化表示生成器φR和动作记分器φA的随机的初始化参数

3. forj=1; 最大迭代次数Mdo

4. 初始化游戏并获得开始状态描述s1

5. fort=1;Tdo

6. 用φR转换st以表示vst

7. if 随机数random()<迭代次数ethen

8. 选择随机一个动作at

9. else

10. 对所有动作，通过φA(vst)计算Q(st;a)

11. 选择at=argmaxQ(st;a)

12. 执行动作at并获得奖励rt和新状态st+1

13. ifrt>0，设置优先权pt=1,elsept=0

14. 存储转移量(st;at;rt;st+1;pt)到D中

15. 从D中随机采样小数量的转换(sj;aj;rj;sj+1;pj)

16. 设置

17. 对损失执行梯度下降步骤L(θ)=yi-Q(sj,aj;θ)2

18. 输出Web服务组合优化方案

4 实 验

4.1 实验设置

本文提出的方法在连续迭代循环中运行，直到达到收敛点。一旦学习代理收到了若干个连续时间的累积奖励的相同值，代理则将收敛到最优策略。这些累积奖励按节进行比较，差异根据阈值进行预测。所有模拟实验都在六核心Intel Xeon 3.2 GHz iMac Pro上进行，具有32 GB的RAM和8 MB的GPU；采用Windows系统运行MATLAB仿真软件，利用MATLAB语言进行程序编写，阈值设置为0.001，迭代次数设置为1 000。

在以下实验中，基于QWS数据集考虑了三个QoS属性，即可用性、可靠性和响应时间。通过使用表1聚合其成员Web服务的QoS向量，计算每个工作流的平均累积奖励r。

表1 聚合参数

在学习质量、选择策略和消耗时间性能方面，将本文方法与文献[5]提出的MO-SCORM方法、文献[7]提出的SDMP-RL方法和文献[8]提出的DQL方法进行比较。学习参数是根据文献[13]中的第一次经验模拟建立的，具体设置如表2所示。

表2 参数设置

4.2 学习质量

本节主要验证所提方法在大型环境中寻找高质量服务组合的能力。当解决方案收敛到最佳服务选择策略时，使用学习代理获得的平均累积奖励来衡量方法能力，此奖励值表示最佳工作流的聚合QoS。

测试分成两次。测试1中，测试环境抽象任务数量固定为150个和250个，其可用的具体Web服务的数量范围为600到900。在此环境下，运行四种方法并将结果统计于图3中。

图3 不同抽象服务任务数量下的积累奖励对比

可以看出，虽然环境规模较大，但本文提出的LSTM-DQN方法的运行结果优于文献[5]、文献[7]和文献[8]方法，LSTM-DQN方法显然在整个学习过程中获得更高的累积回报，并带来更高质量的解决方案。

测试2中，将具体服务的数量固定为700和900，并将抽象任务服务的数量范围设置为100到400，实验结果如图4所示。

图4 不同具体服务任务数量下的积累奖励对比

无论每个工作流的抽象任务的数量大小为多少，LSTM-DQN服务组合方法的结果均优于文献[5]、文献[7]及文献[8]方法。随着抽象任务服务数量的增加，方法性能差距会越来越大，由此验证了LSTM-DQN方法可以找到更好的服务组合、在大型环境中的可扩展性及其查找高质量服务的能力。

4.3 最佳服务选择策略

本节验证所提出的学习方法在动态服务环境中找到最佳服务选择策略的能力，该能力由获得的累积奖励来衡量的。服务环境中的动态更改取决于参与者具体服务的QoS值变化。QoS值动态变化会影响学习代理收到的奖励值r。本实验中用两个因素来衡量服务环境的动态变化，即更改的规模和变化的频率。

为验证变化规模这一因素的影响，考虑一个每个任务包含200个抽象任务服务和700个具体服务的工作流，改变参与者具体服务的QoS值，变化百分比分别为1%、5%和10%。实验结果如图5所示。其中：x轴表示参与者具体服务的QoS值的更改百分比；y轴表示学习代理在收敛到最佳值之前所获得的累积奖励。

图5 变化尺度对比1

可以看出，LSTM-DQN方法在服务环境中汇聚到最佳策略之前，分别累积了162和111个单位的奖励，而服务环境在其参与者的具体QoS值中经历1%和5%的周期性变化服务。与DQN和RL方法在同一环境下分别获得的85和77个单位的奖励，以及64和56个单位的奖励相比，在复杂动态的环境中学习最佳服务选择策略时，LSTM-DQN方法的效率不高。

为验证更改频率这一因素，本文考虑一个每个任务包含200个抽象任务服务和700个具体服务的工作流，参与者具体服务的5%的QoS值每1 000、500和250段落按顺序定期变化。结果如图6所示。其中：x轴表示段落数；y轴表示学习代理在收敛到最佳值之前所获得的累积奖励。

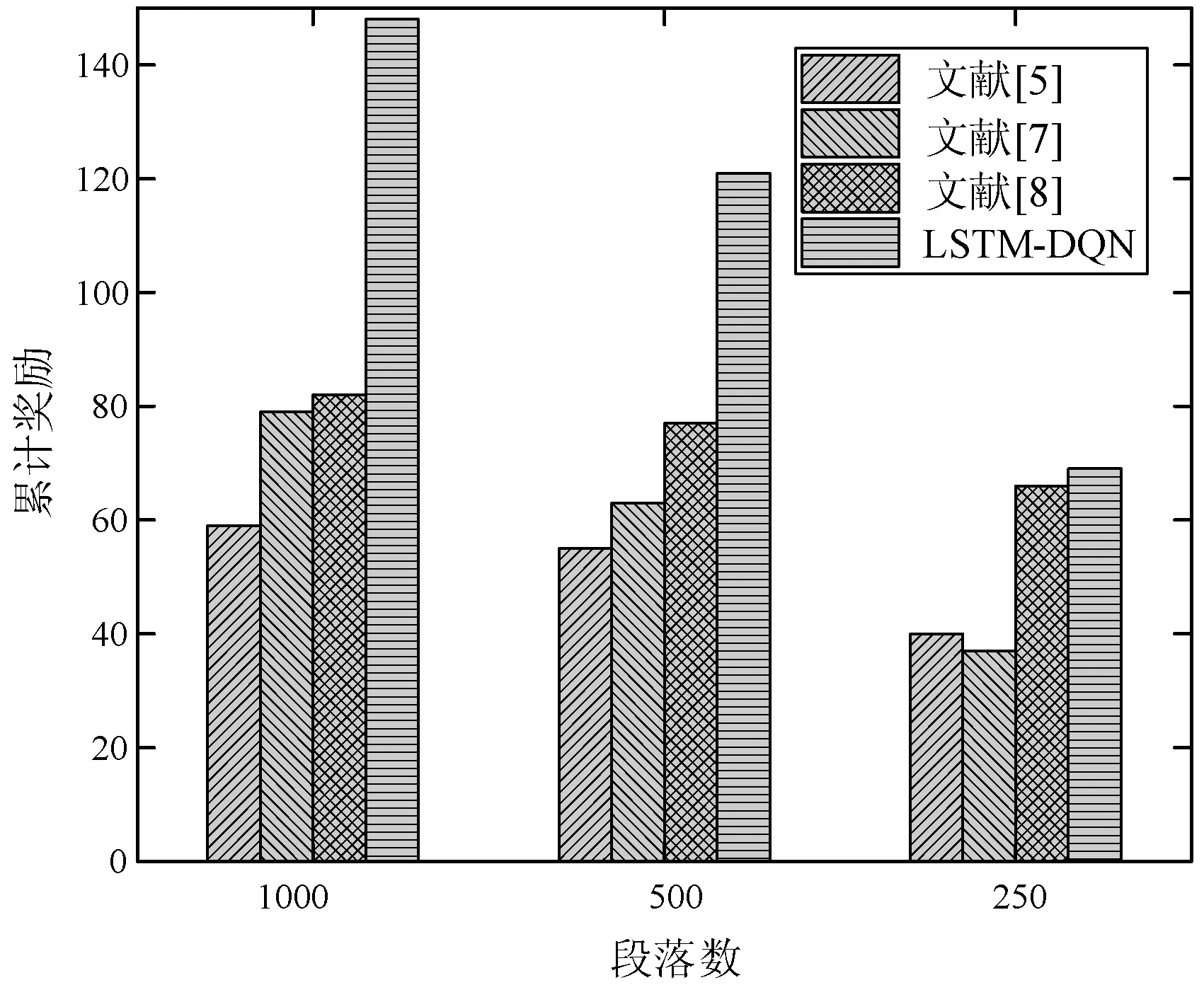
图6 变换频率对比

可以看出，LSTM-DQN方法在汇合到服务环境中的最佳策略，每个1 000段和500段的参与者服务的QoS值分别经历5%的周期性更改。这与DQN方法和RL方法在相同服务环境中分别获得的80和67个奖励单位以及57和53个单位的奖励相比更好。

4.4 服务组合成功率

本文方法在大规模服务数量下效果明显，为了验证这一点，采用不同的任务数对四种方法进行对比实验，实验结果如图7所示。

图7 变化尺度对比2

可以看出，使用LSTM-DQN方法能够得到相对高的服务组合成功率。并且服务组合时，组合成功率与任务数有关系，随着任务数的增加，组合成功率会降低，但使用LSTM-DQN方法组合成功率变化缓慢，说明候选服务数越多，系统的性能越稳定，但系统的代价也会增大，这与实际是相符合的。

4.5 消耗时间

对20个服务组合要求进行20次取样，将LSTM-DQN方法与文献[5]、文献[7]、文献[8]方法进行实验对比，服务组合消耗的时间如图8所示。

图8 服务组合消耗的时间对比

可以看出，随着参与组合服务数目的增加，在网络环境经常变动的情形下，服务组合所耗费时间明显都在增加，但是LSTM-DQN方法与其他两种方法相比，其消耗的时间相对较少，服务组合的数目越多，其优势越明显。

5 结 语

本文提出一种利用记忆单元和改进DQN的Web服务组合优化方法，该法利用Markov对Web服务组合优化问题进行建模，并引入了强化学习的组合优化模型，简化了组合优化过程。并且基于记忆单元对深 度Q网络算法进行优化，提出LSTM-DQN方法，极大地提升了DQN算法的全局寻优能力。为验证所提方法的性能，将其基于QWS数据集与DQN和RL方法进行对比分析，结果表明，本文方法相对于其他两种方法在大规模服务环境下对Web服务组合优化所消耗时间更短，服务组合成功率更高，具有更强的处理能力和处理效率。

本文方法只考虑一个代理的Web服务数量，在未来的工作中，可以考虑将LSTM-DQN方法扩展到多代理设置，并针对学习代理数量与服务环境规模之间的权衡问题作进一步的研究。