基于EGM2008模型处理DEM数据的应用研究

宋学山 柴志勇 王冰 冯迎旭 王雪娇

中水北方勘测设计研究有限责任公司，中国·天津 300222

EGM2008；DEM；高程拟合

1 引言

随着测绘技术的发展，尤其是合成孔径雷达干涉测量技术（简称INSAR）、卫星遥感技术、机载激光雷达（LiDAR）测量技术等成为新兴的空间测量技术，由此获得了数字高程模型（简称DEM）、数字表面模型（DSM）以及数字正摄影像（DOM）等大批量数据产品，具有精度高、信息丰富、直观逼真、现实性强等优点，可作为背景控制信息评价其他数据的精度、现实性和完整性；可从中提取自然信息和人文信息，并派生出新的信息和产品，为地形图的修测和更新提供良好的数据和更新手段；同时克服了传统测绘技术的人力投入大、通视等问题的影响，能够快速、高效地获得空间三维地理信息数据，引起了测绘等相关行业的浓厚兴趣并得到广泛应用。

实际工程项目中，特别是在没有勘测资料的工程区域，为了迅速而有效地实施规划设计，大批量的DEM 数据应运而生。但DEM 数据产品的坐标系统主要为WGS84 坐标系，高程基准为大地高，基于WGS84 椭球参考面，而在实际工程设计中采用的高程基准为正常高，基于似大地水准面。如何实现以WGS 椭球参考面为基准的大地高到以似大地水准面为基准的正常高的转换成为限制DEM 数据应用的常见问题。

本文提出利用最新的EGM2008 地球重力场模型，对已有的DEM 数据进行高程数据转换，以满足实际生产的需要，为以后在无人能到达的区域、面积较大区域、山区或密林区域，尤其是前期资料缺乏无法实施水准的海外项目奠定基础，以期达到快速获取高程，服务前期设计，减少成本，降低人力消耗的目标。

2 基于EGM2008 模型的移去-拟合-恢复法确定区域似大地水准面

2.1 地球重力场模型确定似大地水准面的基本原理

重力场模型可以通过多种表达式来表示，其中使用最多的是球谐展开式。地球重力场模型实则为调和函数，该函数能够不断逼近地球质体外部引力位，并且在无穷远处收敛，极值为零。一般情况下重力场模型可以展开成一个在理论上收敛的整阶次球谐函数的无穷级数形式，而由级数的系数所组成的集合定义了一个与之相对应的地球重力场模型。

使用现有的重力场模型可以很容易的获取大地水准面差距和重力异常值。利用全球重力场模型可以方便的求出任何一点的高程异常值，但这个值通常是含有很大的误差，和真实值之间有一个差值，假设一定数量点的真实高程异常值是已知的，通过真实值与模型值就可以得到这些差值。对这些差值进行数学拟合，用一个数学上的平面或者曲面去逼近这个值，在拟合出来的曲面上求得待求点的这部分差值，最后恢复模型计算出来的中长波部分的高程异常，就可以得到这些点的高程异常。这个过程被概括为移去拟合恢复法。基于此，本文提出了从已知点的高程异常值中去掉高程异常长波部分，对于剩余的短波部分的高程异常值与中波部分整体看作为残余高程异常值，对残余高程异常值采用数学模型进行拟合计算，得到整个测区的残余高程异常函数计算式，再输入任意一点的平面坐标，得到该点的残余高程异常值，再加上EGM2008 重力场模型计算的高程异常值的长波项，从而获取未知点的精确高程异常值，从而实现了大地高到正常高的精准转化[1]。

2.2 基于EGM2008 模型确定似大地水准面的基本原理

该思路综合利用EGM2008 模型及数学拟合方法，无须实测重力数据，只须联测测区少量水准点，尤其是在地形起伏较大、水准联测点较少的地区，能方便地进行GPS高程拟合。根据物理大地测量学理论，高程异常ζ 可以表示为：

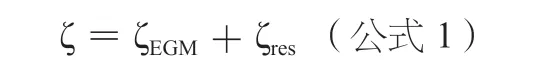
式中，ζEGM是由 EGM2008模型求得的高程异常长波部分；ζres是残余高程异常。

“移去-拟合-恢复”法思路为，从已知点的已知高程异常ζ 中移去ζEGM，获得ζres 进行模型拟合；基于拟合模型计算待求点的ζres，再加上ζEGM，就可得到待求点的高程异常ζ。

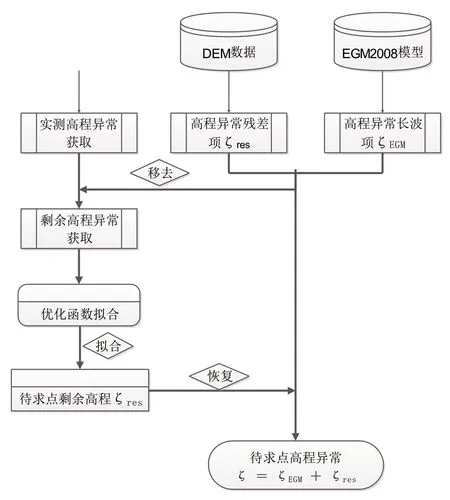
图1 “移去-拟合-恢复”法基本流程图

2.3 拟合优化函数模型

利用高精度EGM2008 重力场模型数据，可以迅速获得测区任意一点的重力高程异常。因此求取精准高程异常值最关键的一步就是残余高程异常值的求取。

任意一点的残余高程异常无法准确获取，只能通过现有的GPS/水准测量方式获取一定数量的区域控制点。通过已知控制点可以获取该区域的残余高程，然后选择合适的数学模型拟合该区域的优化函数模型[2]。

本文选择多项式曲面拟合法作为拟合优化函数模型，其原理是：根据区域中已知点的平面坐标X,Y(或大地坐标B、L)和高程异常值ς，用数学法拟合测区似大地水准面，再内插出待求点的高程异常，从而求得待求点的正常高。多项式曲面拟合的一般模型为：

式中a0、a1、a2、a3、a4、a5、a6、a7、a8、a9、为模型待求参数，ς为已知点高程异常值。

当已知控制点为n 时，其方程式可写成：

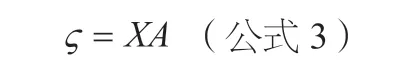
即：

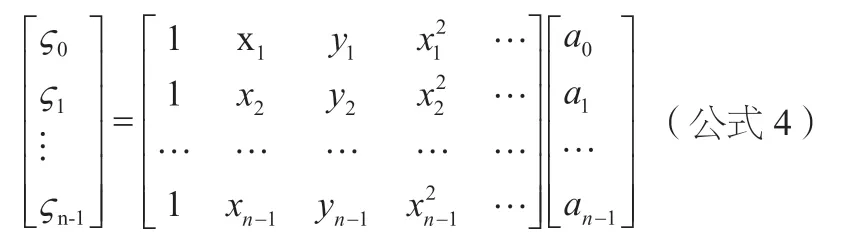
通过高斯消元求出模型参数A，然后代入待求点的平面坐标计算出高程异常值，进而计算出正常高Hr。

当已知控制点数目较多时，采用最小二乘法计算待求参数A，其高程异常值ς与已知控制点平面坐标x、y 关系式可写成：

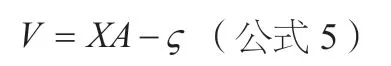
根据最小二乘法原理，可计算得A=(X TX)-1XTς，进而代入待求点平面坐标，计算其高程异常值，然后求出其正常高。

3 平台开发及案例分析

根据上面所述内容，结合本文提出的基于EGM2008 模型的移去-拟合-恢复法求取高程异常值的核心思想，进行了相关程序的编写与计算平台的开发，以人机相互的方式实现高程异常值的计算。开发的平台名称为“基于EGM2008模型处理DEM 数据的程序设计”[3]。

3.1 计算平台的功能

本程序计算平台，利用EGM2008 模型及优化函数拟合，可以实现任何一个区域内DEM 数据大地高到正常高的转换，在此基础上，在测区附近有一定数量已知点的前提下，可以求取区域内高程异常值数学模型，从而进一步精确求取DEM数据的正常高，进而满足实际工程项目需求。

图2 程序设计界面

3.2 案例分析

现以开发的“基于EGM2008 模型处理DEM 数据的程序设计”平台为计算手段，以中国福建省某岸线规划类项目为测试案例，将DEM 点云数据进行了大地高到正常高的转换，并将比对数据进行了分析与研究[4]。

本案例测区地处闽西南上古生代覆盖层低山丘陵地貌，本次选取了8 个已知控制点作为起算数据，控制点分布为面状分布，且基本能够均匀覆盖测区，控制点示意图如图3所示。控制点高程值采用的四等水准连测获取，控制点成果如表1所示。

本项目采用机载LiDAR 技术获取了测区地面基于WGS84 椭球大地高的点云数据，现进行如下计算：

图3 控制点位置示意图

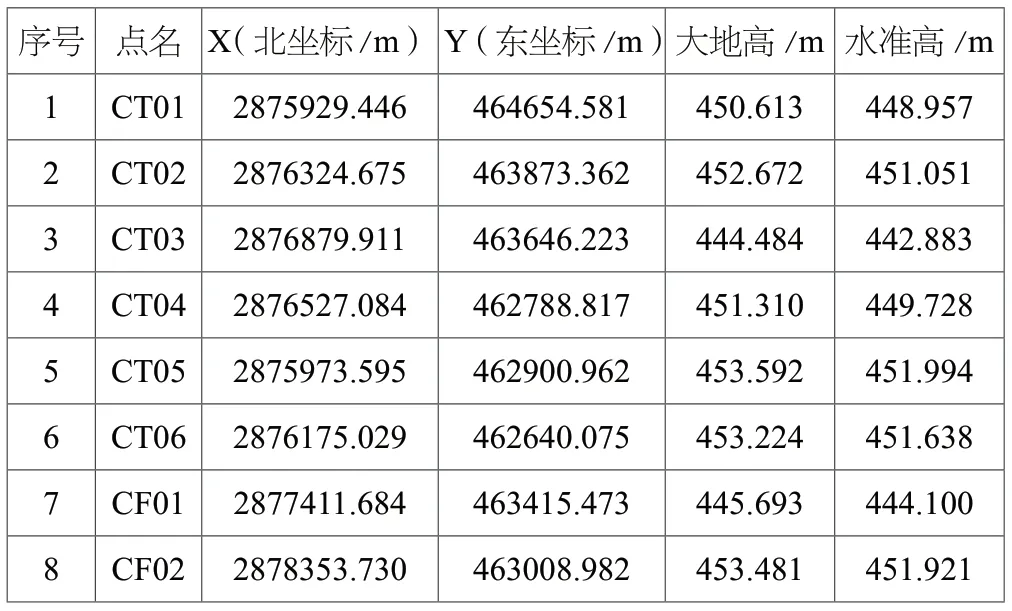
表1 控制点成果表

方案一：将DEM 数据直接通过EGM2008 模型计算器获取EGM2008 高程异常拟合正常高；

方案二：选取测区内所有控制点（8 个）作为已知点，将DEM 数据通过本科研项目开发的计算平台进行处理获取正常高；

方案三：选取测区中心一个控制点（CT03）作为已知点，基于EGM2008 地球重力模型进行单点校正，通过计算平台将DEM 点云数据由大地高转换成正常高；

将上述三种方案的计算后的DEM 数据与DEM 处理后的水准高程值进行对比，对比结果如下：

表2 各计算方案精度指标

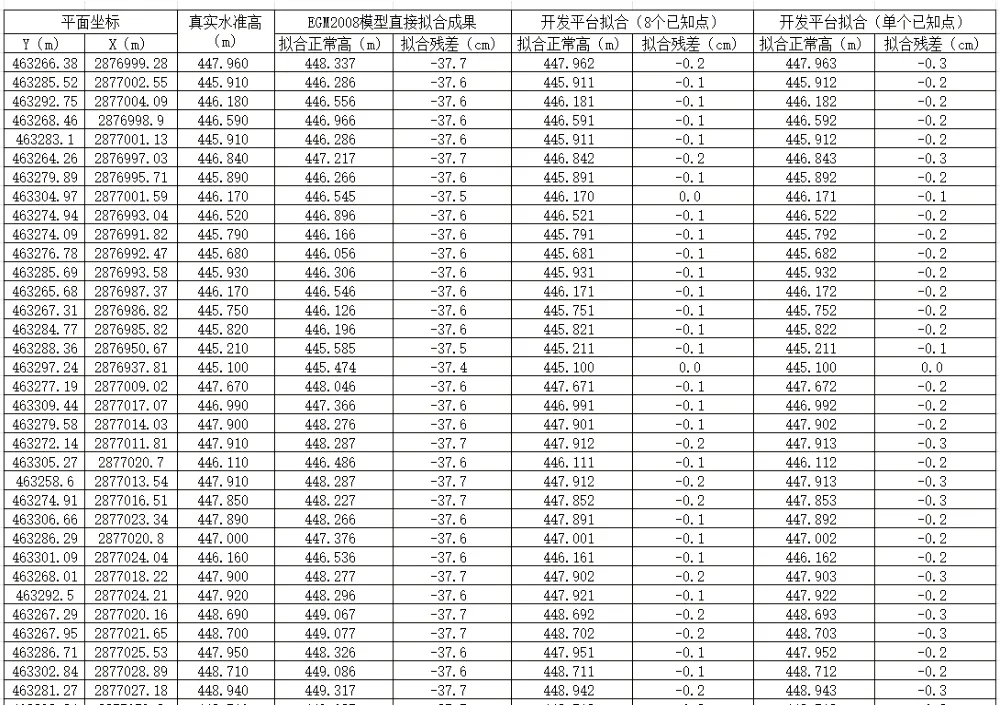
图4 拟合成果部分展示图

由计算成果可以看出，直接用EGM2008 模型拟合计算的DEM 点云数据的正常高误差值较大，拟合中误差为35.56cm；采用本次科研项目基于EGM2008 模型的移去-拟合-恢复法为核心思想而开发的计算平台拟合精度较高，采用测区全部8 个控制点时，拟合中误差为3.35cm，采用单个控制点拟合中误差为3.85cm。

4 结语

通过不同地域、不同地形条件下的案例测试，可以得出无论是在平原、丘陵还是高山区，基于EGM2008 模型的移去-拟合-恢复法的拟合计算方法可以实现DEM 数据的由大地高向正常高的高精度转换，且转换精度能够达到10cm 以内。

在一些由于自然环境恶劣而造成作业困难的项目地区，尤其是一些国际项目中，地处偏远的高山区，已知水准点极少，高程控制难以布设，加之工期非常紧张，而又亟待快速获取基础地形图资料。在无法获得足够的控制点来进行拟合或转换参数求取的情况下，可采用基于EGM2008 模型的移去-拟合-恢复法的拟合计算方法来快速实现测区DEM 数据的大地高向正常高的转换，从而提高项目生产效益。