多跨矮塔斜拉桥悬浇施工中应力监测研究
胡世翔,马文刚
(南京工程学院,江苏南京 211167)
0 引言
矮塔斜拉桥施工中受力复杂,尤其是悬臂现浇施工,结构应力随施工过程不断变化,需要对结构施工应力进行监测,通过对比采集的应力数据和结构理论分析结果,分析结构受力是否和理论分析一致,并监测应力是否超出材料限制[1]。应力监测可以很好地反映实际结构在施工中的应力变化,预警施工安全[2]。
实际应力监测中通过传感器采集数据,施工前需要根据结构受力特点和施工方案,确定布置传感器的位置和数量以及导线的走向方案,施工过程中在相应截面布置对应位置的传感器。一般埋设的传感器为振弦式传感器,直接测得数据为结构应变,需要结合理论计算排除掉非受力应变的影响,最终得到结构的应力值,并应用于结构施工监控[3-4]。
本文结合某四塔五跨矮塔斜拉桥为例,分析了应力监测原理、实测应变中非受力应变处理方法、应力测试误差来源分析,可为类似工程施工监控提供借鉴。
1 桥梁施工中应力测试原理
振弦式应变传感器是目前施工应力监测中最常用的传感器,其基本是一定长度的钢弦放置在钢圆筒内,钢弦两端固定于圆筒内,并处于一定的张拉力中。配套的检测设备连接传感器后,机器可以识读钢弦的频率,而钢弦的频率与长度有关,从而由钢弦频率变化可以计算其长度变化,最后得到应变变化数值。振弦式应变传感器有多种类型,考虑到施工环境和耐久性,钢筒需要密封并保证一定强度。混凝土中需要采用埋置式传感器,施工中牢固固定在钢筋上,并做好浇筑振捣过程中的保护,永久置于混凝土中。
振弦式应变传感器直接测试数据为应变,需要根据混凝土应力应变关系计算实际应力,一维状态下混凝土应力可按公式σe=E∙εe计算,式中:σe表示混凝土应力;E为弹性模量;εe表示弹性应变。但需要注意的是,直接采集到的应变并非弹性应变,而是结构总的应变,不仅包含受力产生的应变,还包含很多其他因素影响,例如温度变化导致的伸缩变形,混凝土收缩产生的收缩应变,混凝土受力后的徐变变形,结构截面存在温度梯度时,产生温度应力。因此在计算结构施工中应力时,需要在实测应变中排除上述因素的影响。
2 桥梁施工中应力测试误差来源分析
施工监控中,混凝土应力实测值和理论值存在一定差异,这一差异的影响因素较多[5],包括计算模型中材料参数和实际结构不一致的原因、施工环境影响、传感器安装影响以及环境因素导致的非受力应变等。这些因素和解决方法具体如下。
2.1 传感器的安装和保护
传感器埋设不仅要位置正确、方向正确,且扎丝等固定方式应符合要求,需要一定技巧和经验以使传感器安装牢固、位置正确,注意导线的走向和固定。由于传感器是在混凝土浇筑前埋设,因此需要注意施工中的保护。
2.2 材料参数修正
理论计算模型一般会采用规范数值[6],该数值和现场实际结构材料存在一定差异,需要根据现场实测结果进行一定模型修正。
2.3 日照和环境温度的影响
温度对应力测试影响包括环境温度和日照产生的温度梯度两部分,环境温度变化使结构整体升温或者降温,可以根据埋设的温度传感器来计算修正。为防止日照导致结构截面上的温度不均匀从而产生温度应力,且截面不均匀温度场精确计算较为复杂,因此要注意选取合理的应力采集时间点,如日出前,以避免影响。
2.4 混凝土收缩、徐变影响
收缩、徐变是混凝土材料的固有属性,需根据材料参数和受力情况,通过理论计算排除影响。
2.5 传感器数据采集影响
应变传感器采集过程也会影响最终实测结果,需要结合施工过程的开展,准确采集初始值和各阶段数据,尤其是初始值的采集会影响后续各阶段的结果。当结构受力状态改变时,例如张拉预应力筋或者浇筑混凝土,应变的采集需要考虑应变滞后的特点,应在受力状态改变后一定时间后采集,并观察数据的稳定性。
2.6 数据采集截面特点的影响
截面形式和截面配筋影响。混凝土截面中会配置相应的受力钢筋和构造钢筋,这些钢筋会影响混凝土局部应力分布,一般的混凝土应力计算过程中采用梁截面假设,并未对混凝土局部应力分布产生影响,对于配筋复杂、受力较大部分可以采用实体有限元进行精细化分析,从而精细分析混凝土的实际应力分布。
3 案例工程施工现场应力实测及分析
3.1 工程背景
某工程为矮塔斜拉桥,共5 跨,中间3 跨跨径150 m,两侧边跨95 m,采用变截面预应力混凝土主梁,根部梁高5.5 m,跨中3.0 m。
3.2 监测截面及测点布置
根据本桥的结构型式、施工程序和受力特点,全桥选择了9个应力状态监测截面,监测截面位置及测点布置分别如图1和图2所示。
3.3 实测应力结果及分析
如前文所述,在各截面埋设传感器并按工况采集应变。现以10 号墩主梁根部截面(见图1 中的截面A、B,各布置14个钢弦式应变传感器)为例,分析应变测试方法和结果。
3.3.1 混凝土收缩、徐变影响修正
混凝土徐变影响是应力监测必须考虑的重要因素,徐变产生的应变大小和受力有关,由于桥梁施工过程中混凝土的应力小于材料应力强度的一半,根据线性徐变假设,徐变应变和混凝土中荷载持续时间成线性正比关系,可采用徐变系数表示二者关系,见公式(1),其中徐变应变εc计算见公式(2)。

混凝土徐变系数φ和收缩量根据规范(JTG 3362—2018)的建议公式确定。混凝土的收缩应变可按公式(3)和(4)计算:
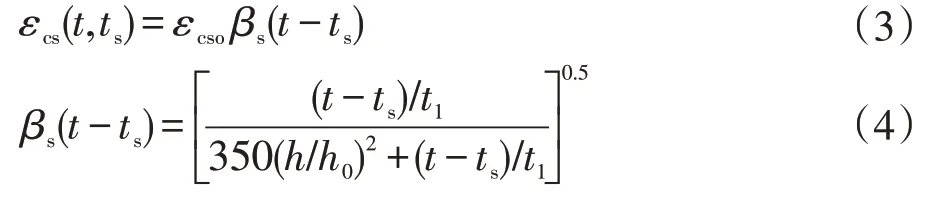

图1 全桥应力监测截面布置

图2 A、B截面应力监测截面测点布置
式中:εcs(t,ts)表示收缩开始时龄期为ts,计算时龄期为t的收缩应变;εcso为名义收缩系数;βs为收缩时间发展函数。
混凝土徐变系数可按公式(5)和(6)计算:

式中:φ(t,t0)表示加载龄期为t0,计算时龄期为t时的混凝土徐变系数;φ0为名义徐变系数;βc为徐变时间发展函数。
3.3.2 温度影响修正
由于混凝土的线膨胀系数与应变计中的钢弦不一致,因而温度变化可引起应变变化,需消除其影响。其修正应变为:

式中:ε0为测量应变;T、T0分别为测量温度、初始读数温度;α0为钢弦的线膨胀系数,取为1.22×10-5/℃;αc为混凝土的线膨胀系数,取为1.0×10-5/℃。
3.4 应力测试结果及分析
根据采集的实测应力结果,采用前述排除非受力应变的方法,经过计算得到截面A和B的混凝土应力分布情况如表1所示,表中数据以拉应力为正。
如图3—4 所示,表示了施工应力和施工过程的关系,应力分别为施工过程对应截面应力理论值和实测值,实测值为已经修正各影响因素后的结构实际受力,图中应力结果以拉应力为正。
由图3—4可知,本案例工程中实测应力和理论计算结果总体吻合良好,两者差异在1.7 MPa以下,而且实测、理论应力随施工过程的进展变化趋势一致,案例工程为悬臂施工浇筑,主梁应力最大发生在根部截面,压应力实测最大值小于材料的允许限值,数值为7.1 MPa。
4 结语
本文在总结分析大跨桥梁结构悬臂浇筑施工中应力监测方法的基础上,重点分析了常用应力传感器测试原理和现场实测应力影响因素,并给出各应力测试影响因素的分析和排除方法。
在此基础上,以某实际工程为例,验证了本文所提应力采集和分析方法,实测、理论应力对比结果可知,实测应力和理论计算结果总体吻合良好,且实测、理论应力随施工过程的进展变化趋势一致,施工中结构应力小于材料限值。论文方法可以为类似工程施工监控提供借鉴。

表1 截面A、B应力实测值

图3 10#墩主梁根部上缘应力随施工过程变化

图4 10#墩主梁根部下缘应力随施工过程变化

