直动式交流接触器结构参数设计与优化
齐 磊,宗 鸣,郝书一,王元军
(1.沈阳工业大学 电气工程学院,辽宁 沈阳 110870;2.辽宁省安全科学研究院,辽宁 沈阳 110004;3.国网辽宁省电力有限公司检修分公司,辽宁 沈阳 110003;4.辽宁电力能源发展集团有限公司,辽宁 沈阳 110017)
目前,直动式交流接触器广泛应用于工业和民用的供配电领域。直动式交流接触器以E 型电磁铁作为基本的电磁机构,通过给励磁线圈通电来实现触头闭合,而开断过程的反力则由弹簧提供。当前关于直动式交流接触器的一个重要关注点是如何实现闭合过程中的触头少弹跳和开断过程中的触头少电弧的目标。而实现这两个目标的关键途径之一就是完善接触器的结构设计,使接触器的吸力和反力能够实现优化配合。目前对接触器结构设计与优化取得了一些研究成果,主要集中在永磁接触器的优化设计上,并采用蚁群算法[1]、动态神经网络算法[2]、粒子群优化算法[3]、神经网络法[4]等对接触器结构予以优化。
本文以CJX1-63交流接触器为设计对象,介绍其电磁铁芯、线圈等各部分的设计因素,并给出定量表达式和设计方法。同时,以减小电磁机构体积为优化目标,基于人工鱼群优化算法的最优搜索功能,获得一组相对优化的接触器结构参数。经优化后,电磁机构体积得到明显减小,并且接触器动态性能依然能够符合实际要求。
1 结构参数初步设计
1.1 E型电磁铁机构
直动型接触器多采用E 型电磁铁,E 型电磁铁具有结构简单、装配便利等优点[5]。其基本结构如图1 所示,机构主要包括静铁芯、动铁芯、激磁线圈等部件。线圈缠绕在静铁芯周围,用于通电建立磁场,然后吸引动铁芯完成闭合过程。

图1 E型电磁铁机构
1.2 开距和超程设计
触头开距δk和触头超程δc一般是根据接触器额定工作电流Ie来选择,其经验公式为

1.3 铁芯截面设计
接触器电磁吸力为

式中,Fx为电磁吸力;B为磁感应强度;ζ为两端铁芯柱与中间柱的截面积比值;S为铁芯中间柱截面积;μ0为真空磁导率。
若选择接触器闭合状态为设计点,由式(2)得到

一般的E 型电磁铁为两端对称布置,中间铁芯柱横截面为正方形,两端铁芯柱横截面积为中间铁芯柱横截面积的一半,因此两端铁芯和中间铁芯的长度满足下式:

1.4 激磁线圈参数设计
激磁线圈参数设计是为了有效保证电磁机构的可靠合闸操作[6]。在触头启动闭合操作时,线圈电流急剧上升,到达触动电流Ic时,机构方能开始运动。因此,需要考虑触动电流安匝数。
在恒磁势条件下的电磁吸力表达式为
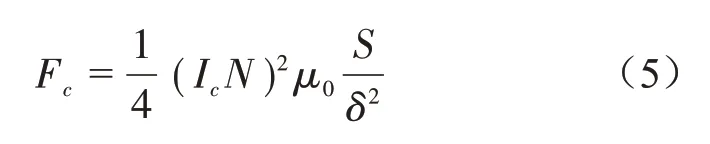
式中,Ic为触动电流;N为线圈匝数;Fc为触动力;δ为工作气隙。
由式(5)可得触动电磁机构的安匝数为

线圈触动电流可以估算,根据式(6)可以计算线圈匝数。线圈窗口面积为
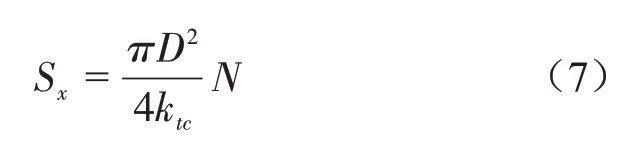
式中,D为导线直径;ktc为填充系数。
线圈宽度不能太宽,一般为铁芯中间柱长度的0.7倍,即

结合式(6)和式(7),线圈高度h4为

取动铁芯高度和静铁芯底柱高度相等,即h2=h3,且要求动铁芯与静铁芯闭合后不能与线圈发生碰撞,即h1>h4。
在实际加工过程中,线圈与铁芯之间应留有缝隙lf,因此动铁芯的总长度为

2 基于目标-约束的人工鱼群优化算法
2.1 目标-约束模型
基于目标-约束的优化属于决策问题,其优化数学模型主要包含3 个基本组成部分:决策变量、目标函数和系统约束。决策变量为关于接触器机构尺寸参数的求解变量,如铁芯长度、高度等。基于目标-约束的优化数学模型就是在满足系统约束条件的情况下,达到目标函数的最优值而确定决策变量的过程[7]。
根据以上描述,交流接触器结构参数的数学模型可表示为

式中,决策变量x∈R;目标函数y∈Rm;gi(x)≤0 为系统约束。
2.2 人工鱼群算法
李晓磊[8]在2002 年提出了模拟鱼群觅食的随机最优搜索算法,即人工鱼群算法。在水域中,鱼在觅食过程中会根据每处食物的多少、其他伙伴的位置等信息来追踪食物。例如,物质营养丰富的海域鱼群会不断聚集,同时鱼也会根据伙伴聚集在某处而判断该位置可能存在较多的食物。由于鱼个体具备的上述特性,在经过一段时间的觅食行为后,鱼群就会全部集中聚集在某一极点。人工鱼群算法就是模仿了这个过程,通过鱼群觅食、聚集等一系列运动,最终人工鱼群寻找到了全局最优值。
人工鱼群算法整体的程序流程如图2所示。
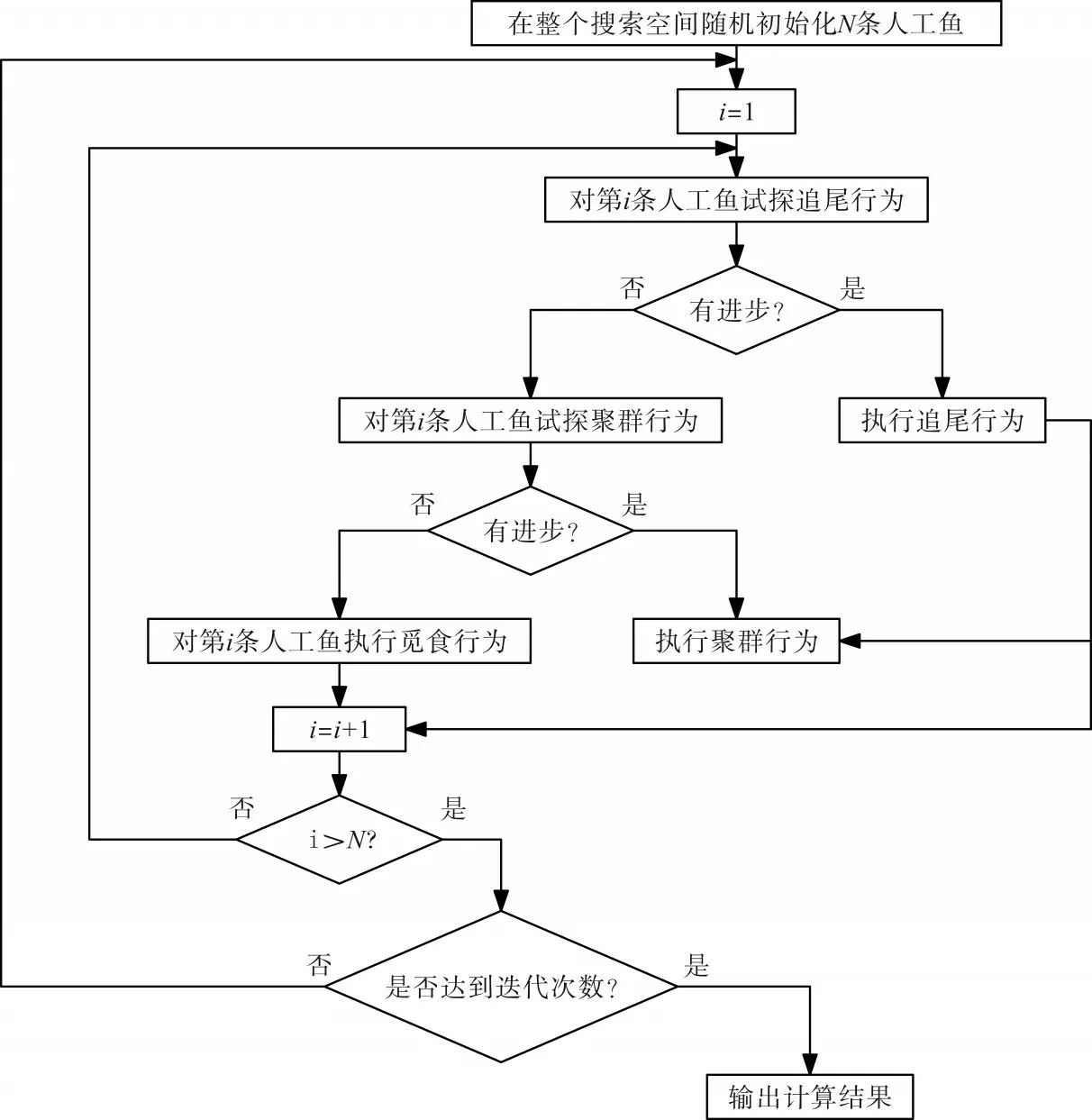
图2 人工鱼群算法整体流程
3 结构参数优化设计
3.1 目标函数
根据图1 所示参数,以电磁系统造价最低为目标,建立目标函数。铁芯体积VFe(x)和激磁线圈体积VCu(x)为

电磁机构的总体积为铁芯体积与激磁线圈体积之和,如式(13)所示:
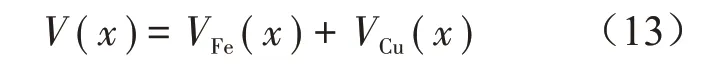
不考虑激磁线圈骨架的质量,电磁机构的总质量为

式中,M(x)为电磁机构总质量;MFe(x)为铁芯质量;MCu(x)为激磁线圈质量;ρFe为铁的密度,取7.8×103kg/m3;ρCu为铜的密度,取8.9×103kg/m3。
电磁机构的总造价P(x)为

式中,PFe为铁芯的成本单价;PCu为激磁线圈的成本单价。
3.2 约束条件
1)电磁吸力约束
为了保证交流接触器的可靠闭合,必须要求在关键位置的电磁吸力要大于反力,如图3 所示。选取的两个关键位置分别为闭合过程中动铁芯经过触动阶段而刚刚开始运动的位置和动静触头刚刚接触时的位置。选取这两个位置的原因,是因为当动铁芯刚刚开始运动时反力弹簧突然起作用而提供反力,而在动静触头接触时,触头弹簧突然起作用与反力弹簧共同使系统反力发生了突变。保证在这两个反力突变点的电磁吸力大于反力,即可基本保证接触器能够可靠闭合。

图3 约束电磁吸力的关键位置
电磁吸力表达式为

式中,Fx为电磁吸力;IN为激磁线圈的安匝数;Gδ为气隙磁导;δ为工作气隙。
忽略磁场的扩散效应,气隙磁导为

结合式(16)和(17),电磁吸力可表示为

激磁线圈电阻R可表示为
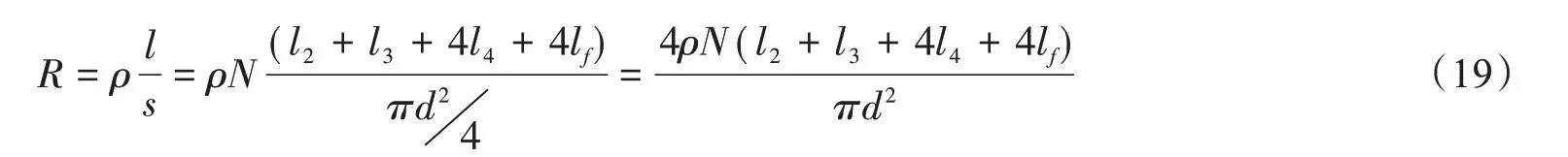
式中,ρ为铜的电阻率;d为激磁线圈铜导线直径。
设UR为最低可靠吸合电压,一般为激磁线圈额定电压的85%,那么

将式(19)代入到式(20)中,得到

将式(21)代入到式(18)中,得到

式(22)表明,电磁吸力Fx可以为电磁机构结构参数表述。
2)温升约束
激磁线圈散热面积A为

交流接触器温升计算公式为

式中,τ为激磁线圈温升;KT为散热系数,取13 W/(m2×℃);P为激磁线圈热功率。
激磁线圈热功率选取为最高运行电压时的发出的功率,交流接触器控制电源电压一般不超过1.1倍的额定值,激磁线圈热功率满足下式:

式中,UN为激磁线圈额定电压;R为激磁线圈电阻。
将式(19)、(23)、(25)代入到式(24)中,整理后得到

式(26)表明,接触器温升τ可以为电磁机构结构参数表述,实际计算时应保证接触器温升小于最大允许温升,即τ<τm。
3)磁感应强度约束
铁芯流过的磁通为

式(27)的比漏磁导为

式中,k为修正系数。
磁感应强度B为
结合式(17)、(21)、(27)、(28)、(29),得到

式(30)表明,接触器磁感应强度B可以为电磁机构结构参数表述,实际计算时应保证磁感应强度小于饱和磁感应强度,即B<Bm。
4 优化结果与实验验证
4.1 优化结果
采用人工鱼群算法对目标函数进行求解,在满足电磁吸力、运行温升、磁感应强度等约束条件下求解最优结构参数变量。计算结果如表1所示。

表1 电磁系统结构参数优化结果 mm
由表1 可知,经过优化,无论是铁芯还是线圈的结构参数均有所减小。通过对目标函数的计算,优化前电磁机构总体积为26.78 cm3,优化后的电磁机构总体积为17.31 cm3,节约体积约为35.4%,用铁量和用铜量均有所减少,降低了装置的总造价,节约了成本。
4.2 实验验证
为了验证交流接触器结构优化后的动态性能是否依然符合实际,分别对接触器结构优化前后的动态性能进行实验测试。接触器激磁线圈输入额定电压为220 V,采用PWM 技术对输入电压进行动态调节,在占空比设置为0.8的情况下,接触器动态性能实验结果如图4所示。

图4 结构优化前后的接触器动态性能实验
图4a和图4b分别为接触器优化前后的动态性能实验情况。从比较来看,结构优化前后的接触器动铁芯吸合时间均为35 ms;优化前后的激磁线圈电流波峰值分别2.75 A和2.9 A,变化率为5.5%;优化前后的电流波谷值分别为1.5 A和1.3 A,变化率为-13.3%。
根据图4,接触器在结构优化前后其动铁芯运动特性未发生改变,而电流虽然产生一定的变化,但变化率不高,且整体的电流波形是一致的。因此,在接触器结构参数改变的情况下,接触器的动态特性未发生实质变化,动态特性对结构参数变化未呈现出很强的灵敏效应。
5 结论
本文重点讨论了交流接触器铁芯和激磁线圈有关结构参数的设计及优化问题。给出了结构参数的基本计算方法,基于目标-约束数学模型,从节约装置成本角度,建立了电磁机构体积的目标函数,在电磁吸力、温升、磁感应强度等约束条件下,利用人工鱼群优化搜索算法,求解一套电磁机构优化参数,优化后的电磁机构体积明显减小。经验证,采用优化后的结构参数对接触器动态性能灵敏度尚不明显,优化后的接触器动态特性依然符合实际要求。

