基于Kaplan-Meier非参数法的海涂湿地生态修复支付意愿生存分析

■王显金

（宁波财经学院，浙江 宁波 315175）

沿海滩涂围垦在实现我国耕地总量动态平衡和为发展我国海洋经济做出巨大贡献的同时，也导致海涂湿地生态系统功能退化、近岸海域生物生境恶化和生物多样性降低等一系列问题。十九大报告中强调，要“强化湿地保护和修复”“建立市场化、多元化生态补偿机制”。研究民众对海涂围垦生态修复的支付意愿及其影响因素，对海涂生态服务价值的间接估算、海涂生态修复民众参与意识的唤醒和生态补偿资金来源的多元化具有重要意义。

一、相关研究文献评述

对海涂湿地生态价值的研究一般采用生态服务功能分类计算法，国内外有代表性的成果如Costanza等（1997）研究得出，全球潮水沼泽湿地生态系统服务功能单位价值为19580美元 /chm2·a，谢高地等（2008）研究得出，2007年中国1个生态服务价值当量因子的经济价值量为449.1元，中国湿地价值当量为54.77。由于分类计算法缺乏完善的理论和技术支持，通过条件价值评估法获取支付意愿（willingness topay，WTP）间接评估生态服务价值在湿地保护或修复中的研究已得到广泛应用。在CVM调查的基础上，于文金等（2011）采用支付能力ELES模型得出居民对太湖湿地生态功能恢复的平均支付意愿为户均支付19.19元/月，基于有序Probit模型得出支付能力是支付意愿的重要制约因素，支付能力与支付意愿之间存在正相关且关联复杂。焦杨等（2012）通过加权平均的方法得到三江平原湿地保护支付意愿为64.57元/(人·a)，综合采用卡方检验和Kendall系数检验方法得出，较之于对湿地的认识问题，受访者的社会情况对支付意愿有更强烈影响。高琴等（2017）利用多项Logit模型评估三江湿地生态系统服务支付意愿得出其范围在 46.06元 /(人·a)至 98.92元 /(人·a)之间，引入行为态度、主观规范等控制变量能更好地解释民众的选择行为。

综合而言，已有研究一般以河流、湖泊湿地而较少以海涂湿地为研究对象，支付意愿的计算方法一般采用函数模型，支付意愿的影响因素较多采用相关分析法、Logit回归和Probit回归等方法。由于实际获得的调查数据，往往难以确定相应的支付函数，所以参数方法往往不可行。故笔者以宁波杭州湾新区海涂生态修复支付意愿为例，基于CVM数据基础，采用生存分析中的Kaplan-Meier非参数法求解支付水平均值，并深入分析影响因素，最后提出海涂围垦生态修复资金筹集的对策建议。

二、基于Kaplan-Meier非参数法的海涂围垦生态修复支付意愿理论模型

（一）生存分析用于支付意愿数据分析的理论依据

生存分析（survival analysis）也称为风险模型或持续模型(hazard model/duration model)，是一种根据实验或调查数据对生物及具有类似于生存规律的其他事物的生存时间进行分析和推断的统计方法。目前生存分析已广泛应用于生物统计、交通、医学和金融等多个领域。广义的生存时间指生物体存活的时间，或所关心的某种现象的持续时间。生存分析用于支付意愿数据分析主要基于以下两点原因：第一，支付意愿是指从支付水平为零开始，一直到该支付水平的持续区间，属于广义生存时间范畴，可运用生存分析方法来对其进行研究。第二，CVM方法得到的支付意愿数据往往包含如支付意愿大于某值、小于某值或者在某一区间内等删失数据（censored Data），生存分析能综合删失数据的有用信息而不是简单的摒弃，因而有独特的优势。

生存分析用于CVM数据分析，需把支付意愿视为生存时间。如果支付意愿t服从指数分布、Weibull分布、对数正态分布等某一特定的分布，则可以采用参数法获得生存率的估计值；而实际情况往往是生存时间的分布不符合上述所指分布，则不宜用参数法进行分析，应当用非参数法，其优点为不论总体的分布形式和参数如何均可使用。生存分析非参数法包含寿命表法和Kaplan-Meier法，前者主要用以分析总体的生存规律，后者不仅可以分析总体的生存规律，而且可以分析寻找相关影响因素（张文彤，2013）。故本文采用Kaplan-Meier非参数法。

（二）基于生存分析的支付意愿生存函数和风险函数

设T为一个非负的随机变量，代表居民对海涂围垦生态修复的支付意愿。F(t)为T分布函数，f(t)为T相应的概率密度函数。T的生存函数为描述支付意愿统计特征的基本函数,也叫生存率(survival rate)，定义为：S(t)=P(T＞t)=1-F(t),0＜T＜∞)，它是一个非增函数。

（1）连续性支付意愿生存函数和风险函数

危险率函数定义为描述观察个体在某时刻存活条件下，在以后的单位时间内死亡的（条件）概率：

（2）离散型支付意愿生存函数和风险函数

离散型支付意愿生存函数是非增的阶梯函数，设T取值为 a1＜a2＜∧，则 f(ai)=P(T=ai),i=1,2,∧,ai处的危险率为累积危险率函数定义为

（三）支付意愿平均值的Kaplan-Meier法

Kaplan-Meier分析方法，又称PL法、乘积极限估计或最大似然估计法，是由Kaplan和Meier在1958年提出的一种求生存函数的非参数方法。乘积极限法（Kaplan-Meier）适用于离散数据，它用于建立时刻t上的生存函数。Kaplan-Meier法是根据t时刻及其之前各时间点上的条件生存率的乘积，来估计时刻t的生存函数S(t)和它的标准误SE[S(t)]。

假设共有n个支付意愿样本，这些样本的支付意愿共有t个不同的值，将它们从小到大排序为t1＜t2＜∧＜tk，令 dj为支付意愿落入[tj,dj+1]区间内的样本数，nj为支付意愿大于tj+1的样本数，生存函数的乘积极限估计表达式为：

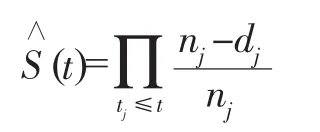
生存函数的标准误的估计公式为：

（四）支付意愿影响因素的非参数检验

一般而言，基于不同社会特征和对生态修复价值认知度有差异的个体的支付意愿往往存在差异。比较多个生存分布有许多非参数检验方法。本文以广泛应用的Cox-Mantel方法来检验多个生存分布的差异性。以比较两个生存分布的一致性为例，假设1和2表示不同的均为n1两类个体，x(1),x(2),∧,x(n1)是第一类个体的n1个支付意愿样本，y(1),y(2),∧,y(n1)是第二类个体的n1支付意愿样本。假设两类样本的观测值分别来自生存函数S1(t)和S2(t)，其原假设和备择假设分别是H0∶S（1t）=S（2t）;H0∶S（1t）=S（2t）。

设 t(1)＜t(2)＜∧＜t(k)是两类样本组合在一起后不同的支付意愿，m(i)表示支付意愿等于t(i)的个数也即t(i)的重复次数，所以

设R（t）是支付意愿t的风险集，即支付意愿至少是t的所有个体组成之集。设n1t和n2t分别是R（t）中对应于类别1和类别2的个体数。在R（t(i）)中的个体数是这里A(i)是R(t(i))中属于类别2的个体所占的比例，令可以证明近似服从标准正态分布。因此若Z＞Z1a/2，则拒绝原假设，两类别有显著差异，推断类别1和类别2的分布不一致。

三、实证研究

（一）数据来源

本研究选取杭州湾新区海涂湿地为研究区域。该区域位于江浙沪城市圈的几何中心，是国家打造湾区经济的重点对象，是国家改革开放的前沿阵地，当前该区域所处的杭州湾南北两岸海涂围垦如火如荼地在进行，同时也是影响东海污染的重灾区。

问卷分为两部分，第一部分为人口学信息，主要问题见表1。第二部分采用支付卡法作为引导技术，调查居民对杭州湾海涂生态修复未来五年的年支付意愿。

为了使假想市场尽可能接近真实市场，本次调查采用面对面形式，调查对象主要为杭州湾国家湿地公园游客、杭州湾新区及其周边各镇居民，调查时间为2019年9月1日至10月16日，采用随机发放问卷的方法，在发放的720份调查问卷中，由于采用面对面的调查方式，问卷反馈率很高，排除一些有明显错误(前后回答矛盾、错答漏答)的问卷后，回收有效问卷670份，有效率为93.1%。

表1 人口学信息

对调查所得的基础数据进行处理，得到670个支付意愿样本。样本的最小值即支付意愿为0元，共计81个样本，占12.1%；最大支付意愿为200元，共计19个样本，占比2.84%。

（二）支付意愿总体分布规律

运用前述介绍的生存函数Kaplan-Meier非参数估计方法，可求出支付意愿的生存函数和危险率函数。附表1所示为样本值在200元以内的支付意愿生存函数及危险率函数的估计值，图1所示为生存函数和危险率函数随着支付意愿的变化规律。

由图1和附表1可知，支付意愿在0-20元范围内，生存函数递减速度快，相应危险率函数递增速度快，约70%的居民支付意愿在20元以内。

图1 海涂修复支付意愿生存函数和危险率函数

附表2 给出了支付意愿的平均值为27.38元，其95%的置信区间为（24.39,30.37）元。而支付意愿的中位数（50%分位数）为7.50元，其95%的置信区间为（6.18,8.82）元。进一步得到25%、50%、75%分位数时的支付意愿为35.00元、7.50元、2.50元。

（三）支付意愿的影响因素

附表3 所示为支付意愿的影响因素显著性分析，图2为相应不同组别的生存函数。

由附表3可知，女性支付意愿均值为29.331元，高于男性支付意愿24.746元，但二者之间无显著性差异（P>0.05）。这一点与研究结论一致。

图2 不同影响因素下海涂修复支付意愿生存函数比较

年龄对支付意愿的影响具有显著性差异（P<0.01），由高到低依次为老年组（≥60岁）、青少年组（≤30岁）和中青年组（31-59岁），支付意愿均值分别为45.23元、26.03元和24.75元。究其原因，老年人支付能力较强，且往往有充裕的时间通过旅游等方式享受海涂湿地的生态价值，从而表现出较强的支付意愿。而中青年人虽然也具备一定的支付能力，但是该年龄段的人往往需要承担一定的家庭经济职责，从而支付意愿相对保守。

受教育程度和家庭月收入均对支付意愿有显著的正向影响（P<0.001）。研究生学历、本科学历和中小学学历的居民支付意愿分别为71.67元、25.56元、20.70元。

高收入（3万元以上）、中收入（1万—3万元）、低收入（1万以下）家庭居民支付意愿依次为48.38元、34.39元、23.87元。

对生态价值的认知程度的不同对支付意愿的影响无显著差异，但了解海涂湿地生态价值的居民支付意愿（34.84元）高于一般了解者（26.32元）和不了解者（25.98元）。

四、结论和建议

（一）结论

本文通过调查杭州湾新区海涂湿地围垦后生态恢复区域居民支付意愿，采用非参数分析中的Kaplan-Meier方法，建立了基于CVM数据的生存分析模型，Kaplan-Meier法直观地展现支付意愿生存函数变化的过程,可客观评价居民的支付意愿。主要得出如下两个结论:

（1）区域居民对海涂湿地修复的平均支付意愿为每人每年27.38元，支付意愿的25%、50%、75%分位数为35.00元、7.50元、2.50元。居民支付意愿主要集中于20元以内。

（2）性别对支付意愿无显著影响；对海涂湿地的生态价值的认知程度对支付意愿虽无显著影响，但了解程度越深，支付意愿越大；家庭月收入和受教育程度对支付意愿有显著的正向影响；年龄对支付意愿影响显著，老年人的支付意愿相对较强烈。

（二）建议

根据本文的研究结果，对海涂湿地的生态修复和保护提出如下建议，为政府制定海涂开发、保护和生态修复政策提供参考：

（1）要充分重视海涂湿地的生态修复和保护。这是当代中国蓝色海洋战略实施中解决海洋环境问题和海洋经济发展相互矛盾使之协调发展的重要手段。民众对海涂湿地修复的热情还不够，支付意愿总体偏低，需要通过旅游参观、宣传教育等手段唤醒民众的湿地环境保护意识。

（2）居民对湿地修复的支付意愿是海涂保护资金来源多元化的途径之一。目前杭州湾新区通过营造景观林、人工湖以及要求入住企事业单位的绿化面积不低于单位占用面积30%等规定卓有成效地部分修复了相应区域湿地的生态服务功能。随着对开发区环境保护的呼声日愈强烈，资金缺口是一个重要的问题，居民的支持为生态保护资金募集提供了一个重要的思路。

（3）湿地的生态价值是制定湿地生态补偿的重要决策依据，在当前直接测量湿地生态价值尚缺乏科学的理论和技术支持的情况下，居民对湿地生态保护的支付意愿间接地反映了湿地的生态价值。

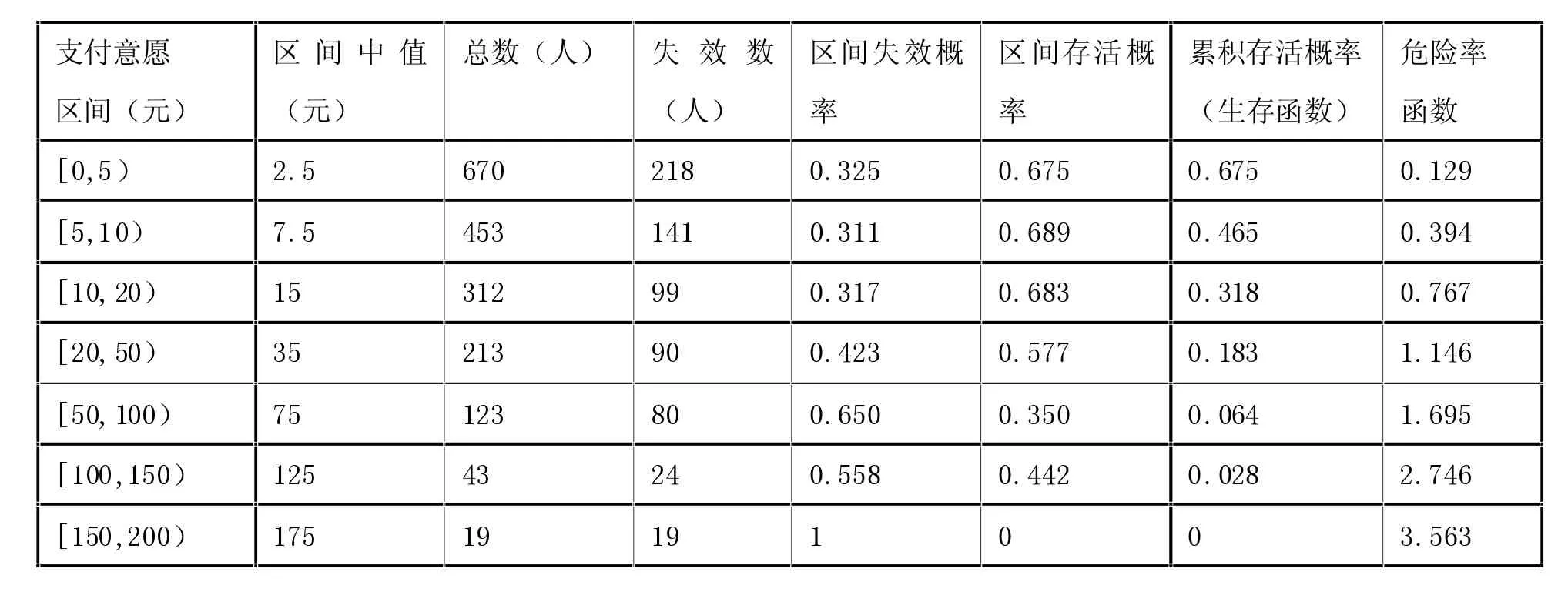
附表1 杭州湾新区海涂湿地生态修复支付意愿的生存函数

附表2 支付意愿的平均值和中位数

附表3 支付意愿的影响因素显著性分析