移动互联网环境下轻量级SM2两方协同签名
冯 琦 何德彪 罗 敏 李 莉
1(武汉大学国家网络安全学院 武汉 430072) 2(密码科学技术国家重点实验室 北京 100878)
根据GSMA移动智库(GSMA intelligence)实时数据[1],目前全球有超过51.3亿人拥有移动设备(即全球66.53%的人口拥有移动设备,如手机、平板电脑或支持蜂窝网络的物联网设备).通常情况下,移动设备通过无线通信与各种服务提供者(如数字货币交易所、DNS、网络购物等)进行通信.然而,开放的网络连接和简单的设备安全部署使得移动设备极易成为网络攻击的目标.因此,服务提供商在提供服务之前,往往需要移动设备向服务器做身份认证,以保证移动网络服务的安全性和可靠性.
数字签名伴随着网络安全的需求而出现,其作用类似于传统的手书签名或印章的电子标记,可以在网络世界中达到与手写签名类似的作用,在信息安全,包括身份鉴别、数据完整性、抗抵赖性等方面,特别是在大型网络安全通信中的密钥分配、身份鉴别及电子商务系统中具有重要作用.相较于其他公钥密码体制,椭圆曲线密码体制(elliptic curve cryptography, ECC)[2]的安全性可以归约到椭圆曲线群上的离散对数困难问题,同时具有密钥长度短、计算速度快等优点,适用于资源受限的移动设备.
在数字签名中,密钥是实施安全身份和消息认证的基础,而密钥泄露往往给网络攻击者可乘之机,例如当密钥泄露并且数字签名被应用于恶意软件时,它会欺骗扫描下载的浏览器过滤器和防病毒软件,让设备认为它来自可信媒介[3].在移动互联网环境中的移动设备,例如智能手机、平板电脑等终端设备自身也存在一些安全隐患:1)移动设备易丢失或被盗,导致内部包含的密钥易丢失或被窃取;2)移动设备搭载的操作系统及第三方程序可能存在漏洞,易被攻击者利用从而实现冷启动等攻击,导致用户密钥信息泄露;3)移动设备可能包含恶意软件,导致用户执行数字签名时数据被攻击者截获.
传统的密钥安全解决方案有2种:1)将密钥存储在外部硬件令牌(U盾、智能卡等),但存在携带不便且成本高的问题,难以应用到移动设备中;2)使用协同签名的思想[4],即存在2个及以上设备分别存储密钥的一部分,数字签名由参与方协同完成,任何参与方都无法掌握完整密钥,这种方法有效保证了在单个设备被恶意实体控制的情况下用户密钥的安全性.
SM2是中国基于椭圆曲线的公钥密码标准,由国家密码管理局于2010年发布,相关标准为“GMT0003—2012《SM2椭圆曲线公钥密码算法》”[5],目前是中国国家密码标准(GBT 32918—2016),其中数字签名算法同时还收录于国际标准ISOIEC 14888—3:2018《信息安全技术带附录的数字签名第3部分:基于离散对数的机制》中.中国二代身份证已全面使用SM2数字签名技术提供身份鉴别.此外,《中国人民共和国密码法》第二十七条明确了关键信息基础设施应当使用商用密码进行保护,网络产品及服务相关密码国产化成为大势所趋.因此,本文针对SM2签名算法设计协同签名协议,为SM2签名密钥的安全存储和使用提供一种高效的解决思路.
本文的主要贡献有3个方面:
1) 针对移动互联网环境下的特殊需求,设计一种轻量级的非平衡SM2协同签名方案,客户端在服务器的帮助下协同完成签名,且不暴露密钥信息.
2) 对设计的协同签名协议提供了完整的安全性证明,结果表明我们所提方案可以有效保护SM2签名密钥.
3) 相关功能、性能的测试结果表明提出的SM2两方协同签名以较小的性能代价提高了密钥的安全性,具有较好的应用价值.
1 国内外相关工作
基于门限秘密共享的分布式签名由Shamir教授于1979年提出[6],经过持续的研究已经有丰富的理论成果.最初的门限秘密共享指的是n个实体分别持有私钥的一部分,当且仅当超过阈值t个被分割密钥才可以恢复完整私钥,完成签名或解密操作.但是一旦私钥被恢复,持有完整私钥的那一方就可以在其他实体不知晓的情况下任意使用私钥,带来极大的安全隐患.
因此,MacKenzie和Reiter教授[7]首次提出针对DSAECDSA的两方签名协议,私钥同样是分割存放在2个实体中,但是签名操作无须私钥恢复,而是通过双方交互式协议的方式完成,同时保证了协议执行过程中没有泄露双方持有私钥碎片的信息.随后,经由Gennaro和Boneh等学者[8-9]的努力,DSAECDSA签名协议得到(t,n)门限框架上的扩展.但是他们使用的分布式Paillier密钥生成使得整体性能较差,Lindell教授[4]于2017年在密码学会议CRYPTO上发表了一个改进的两方ECDSA协同签名方案,仅依赖Paillier的同态加密功能,完成2个实体协同产生公钥和签名的过程,极大提高了协同签名的性能.
自此,门限签名以其优越的密钥保护特性受到学者们的广泛关注.Doerner等学者[10]提出了基于秘密共享和不经意传输协议的(2,n)门限ECDSA签名方案和(t,n)门限ECDSA签名方案.与以往使用同态加密的方案相比,Doerner等学者[10]使用基于Simplest Oblivious Transfer[11]和KOS[12]的隐私乘法协议,在计算性能方面做出了优化.同年,Gennaro等人[13]和Lindell等学者[14]分别发表了新的(t,n)门限ECDSA签名方案,并在基于模拟的模型下证明了协议的安全性.
此外,国内外学者还提出了针对其他密码算法的密钥安全解决方案.Frederiksen等学者[15]提出了一种相对高效的两方RSA密钥生成方案.但是,该方案需要多次使用Paillier同态加密算法,带来较高的通信和计算开销,而且无法扩展到多方框架.针对IEEE P1363标准中基于身份的数字签名,Zhang和He等学者[16-17]先后设计了2种两方协同签名方案,前者仍沿用基于同态加密的方法实现密钥的安全保护,而后者在此基础上取消了同态加密的协助,极大提升了协同签名的速度.随后,Feng等学者[18]利用加法秘密共享的思路,将IEEE P1363标准中基于身份的数字签名协议扩展到了多方.
针对中国数字签名标准SM2,Zhang等学者[19]提出了SM2数字签名算法的两方协同签名方案,但是签名过程中同样需要使用Paillier同态加密操作,方案的执行效率较低.尚铭等学者[20]设计的SM2门限密码算法,因其交互次数过多而导致计算和通信代价相对较大.综上所述,国内外学者在基于门限签名的密钥保护方面已经取得一定的研究成果,但这些成果难以适用于计算和存储资源受限的移动终端.
2 基础知识简介
本节我们主要介绍与论文设计方案相关的基础知识.
2.1 SM2数字签名
根据《SM2椭圆曲线公钥密码算法》规范,SM2数字签名的定义为:
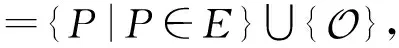
G是G上阶为n的基点(生成元).
H:{0,1}*→Zn是输出整数的Hash函数,H256:{0,1}*→{0,1}256是输出256 b比特串的Hash函数.
SM2私钥表示为随机数d←RZn,对应的公钥为Ppub=d×G.消息M∈{0,1}*的SM2数字签名σ=(r,s)的生成步骤如下:
1) 计算e=H(Z‖M),其中Z=H256(ENTL‖ID‖a‖b‖xG‖yG‖xpub‖ypub)是将用户字节长度为ENTL的身份标识符ID,椭圆曲线参数a,b,G的坐标xG,yG和公钥Ppub的坐标xpub,ypub使用Hash函数计算而来的256 b长的Hash值;
2) 生成随机数k←Zn;
3) 计算(x1,y1)=R=k×G;
4) 计算r=(e+x1) modn,s=(1+d)-1×(k-r×d) modn.若r=0,r+k=n或s=0则返回第2)步.
5) 签名结果为σ=(r,s).
2.2 安全两方计算
安全两方计算(secure two-party computation, 2PC)由姚期智教授于1986年提出[21-22],是指2个参与方在无须进行数据归集的情况下完成数据协同计算,同时保护数据所有方的原始数据隐私.协议双方在数据保留在各自本地的情况下,执行既定的计算逻辑并获得计算结果,其隐私性要求为:在计算完成后,计算双方除了自己的输入数据、自己输入数据相关的中间结果和输出结果外,无法获知任何额外的有效信息.针对签名算法的形式化描述为:计算双方分别持有私钥d1,d2,当确定待签名消息M后,共同计算签名逻辑fsign(M,d1,d2),得到正确的签名值σ=(r,s).
该过程要求2PC签名协议满足:
1) 数据隐私性.协议执行过程中的中间数据及结果都不会泄露关于d1,d2的相关信息.
2) 健壮性.诚实执行协议后,参与方输出正确的签名结果σ.
3) 兼容性.不改变签名结果的形式,使用原始验证算法可正确完成签名验证.
这3点可以保证数字签名过程中所需满足的密钥保护要求,以及2PC签名协议在工程化实现中所需达到的便捷性.
3 安全模型与设计目标
本节详细描述了安全性证明所基于的安全模型和本文方案的设计目标.
3.1 安全模型
本文协议的安全性证明框架是基于游戏的MPC安全证明模型[23-24],即通过构造模拟协议,利用与敌手的交互,将安全性归约到原始签名方案的安全假设.
1) 通信模型
假设系统参数(以及SM2的标准参数)可以通过高效、安全的方式传递给所有参与方.此外,还有一个连接着2个参与方的点对点通道来承载协议的交互.
2) 敌手能力


3) 安全目标


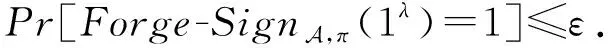
(1)
协同签名方案的定义为分布式签名生成方法,而输出的签名在原验证算法下也是有效的.由此同样可以定义协同签名方案的存在性不可伪造.

与EU-CMA定义不同的是,敌手可以看到腐化方的密钥生成和签名协议实例的视图.定义2遵循基于游戏的MPC安全证明模型.此外,基于现有框架[26],可以将本文设计的协议扩展到一个更强的基于模拟的安全性证明,但是复杂度也有相应地增加.
3.2 理想功能
本文将基于零知识证明理想功能,承诺-零知识证明理想功能完成SM2两方协同签名的构造以及安全性证明.
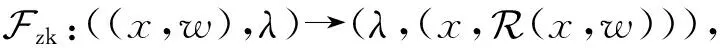
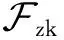
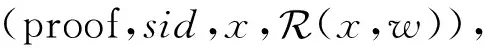
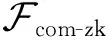
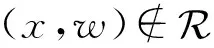
② 当接收到来自U(或S)的指令(decom-proof,sid).如果查询到(sid,U(或S),x)则向另一参与方S(或U)发送(decom-proof,sid,x).
DLOG={(G,G,n,P,w)|P=w×G},
其中,G是群G上阶为n的生成元.关于DLOG的证明可以使用经典的Sigma协议[27],同时利用Fiat-Shamir框架[28]实现非交互式的零知识证明.此外,任意一个通用可组合安全的承诺方案[29-30]均可以满足本文关于安全性的需求,例如在随机谕言机下,使用一个Hash函数H和随机数r即可定义关于x的承诺Com(x)=H(x,r).
4 两方SM2签名方案设计
在本文设计的协议中,生成SM2数字签名涉及2个参与方:客户端U和服务器S.协议内容包括密钥生成协议和协同签名协议,其中密钥生成协议执行一次,协同签名协议可以执行若干次.我们并未改变SM2签名方案的系统参数及椭圆曲线,关于SM2的系统初始化部分则可参考《SM2椭圆曲线公钥密码算法》规范.
4.1 密钥生成协议
SM2密钥生成算法由客户端U和服务器S共同参与完成.具体流程图如图1所示:
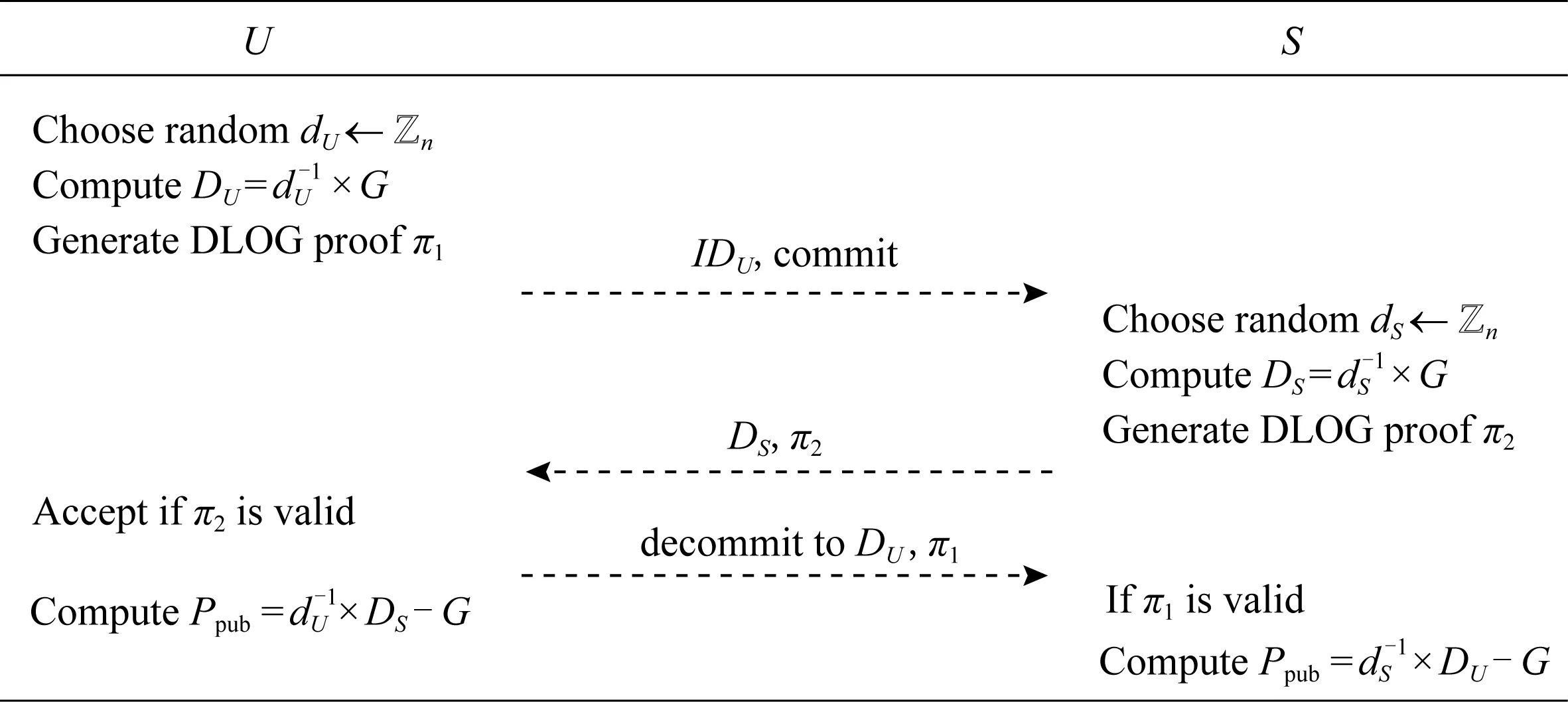
Fig. 1 The workflow of distributed key generation protocol图1 密钥生成协议流程图
1)U→S:{IDU,承诺}

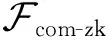
2)S→U:{DS,π2}
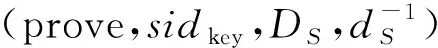
3)U→S:{DU,π1}
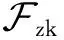
4)U和S输出公钥:
4.2 协同签名协议
客户端U和服务器S在本阶段利用密钥生成阶段的密钥信息,协同产生关于消息M的SM2签名,并由客户端U输出最终签名结果.具体流程图如图2所示.
1)U→S:{e,承诺}
①U计算e=H(Z‖M),生成随机数kU←Zn,计算KU=kU×G.
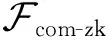
2)S→U:{KS,π4}
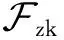
3)U→S:{KU,π3}
4)U→S:{r,s′}
②S向U发送{r,s′}.
5)U输出签名σ:
①U计算s=dU×(s′+kU)-rmodn,令σ(r,s).
② 使用SM2签名验证算法,验证σ是否为关于M的有效签名.若验证正确,那么U输出签名σ;否则U终止会话.
Fig. 2 The workflow of distributed signing protocol图2 协同签名协议流程图
注:一次协同密钥生成需要3次通信,协同签名协议需要4次通信.若是在半诚实模型下,即参与方仅分析获取的消息,但会诚实执行协议,那么就不需要承诺和零知识证明,此时一次协同密钥生成仅需2次通信,协同签名协议需要2次通信(步骤2和4可以合在一起,而KS也无需发送).
4.3 正确性分析
根据密钥生成协议,有:
根据协同签名协议,可得:
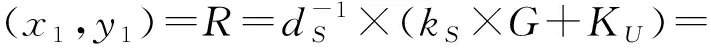
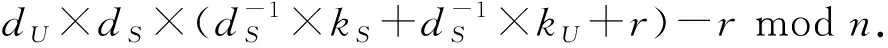
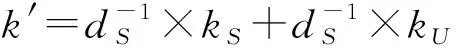
5 安全性证明
本文所设计的协同SM2签名方案的安全性是基于原始SM2签名方案的可证明安全性.
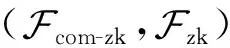

5.1 S腐化

1) 模拟密钥生成
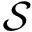
2) 模拟协同签名
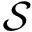
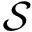
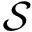
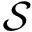
3) 不可区分性分析

4) 伪造

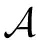
5.2 U腐化

1) 模拟密钥生成
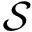
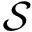
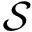
2) 模拟协同签名
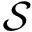
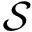
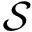

3) 不可区分性分析
4) 伪造

5.3 小 结
证毕.
6 实验与结果
本节针对第4节所设计的协同SM2签名方案进行性能评估,此外还与原始SM2签名方案做了比较.测试所基于的参数遵循《SM2椭圆曲线公钥密码算法》规范中关于素数域Fp上的椭圆曲线定义,椭圆曲线的阶n为长度32 B的大整数,椭圆曲线点的长度为64 B(通过对坐标的压缩可以简化为33 B),Hash函数采用SM3算法.本文测试程序的构建基于开源密码学库MIRACL[31],测试环境为一台配置有64位Window10操作系统,Intel®CoreTMi5-8265 CPU@1.60 GHz,8.00 GB RAM的惠普笔记本电脑.
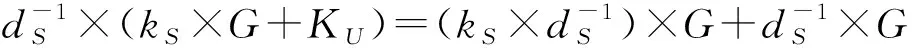
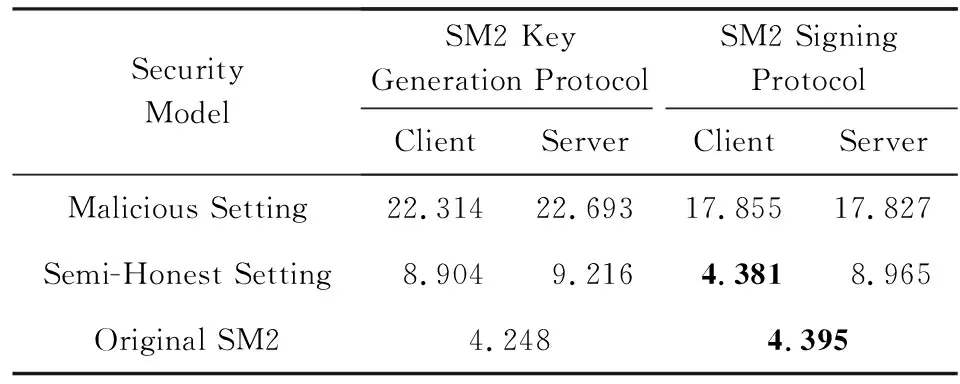
Table 1 Runtime of Our Proposed Protocol表1 本文协议计算性能的评估结果 ms
接着,我们统计分析了协议在恶意模型和半诚实模型下的计算复杂度,如表2所示.根据协议设定,恶意模型下的密钥生成过程中,客户端与服务器之间相互发送一个椭圆曲线点和关于它的零知识证明,此外还有客户端向服务器发送的承诺;而签名比密钥生成多了服务器向客户端返回的(r,s′).表2所示的恶意模型通信复杂度中,括号中表示的是将椭圆曲线点进行压缩以后的通信量.同样,当去掉零知识证明后,通信复杂度也可以减到100 B以内.

Table 2 Communication Overhead of Our Proposed
总体来看,由于把私钥求逆的步骤放在密钥生成阶段中,因此密钥生成阶段的计算复杂度相对较高.但是在实际生活中密钥的生成并不频繁.而本文签名协议在客户端的性能几乎接近于原始SM2签名,因此对于用户设备来说有着非常小的计算压力,由此可见本文设计的方案在非平衡的客户端服务器构架中有较好的应用前景.
7 总 结
为了保护移动互联网环境下用户存储于客户端的SM2密钥,本文基于协同签名的思想,设计了一个轻量级的SM2两方协同签名方案,它允许客户端和服务器在不泄露各自部分签名密钥的情况下共同完成SM2数字签名,产生签名的过程须由双方同时参与,生成签名的过程中也没有恢复过完整的签名密钥,充分保证签名密钥的安全性.此外,我们将协同签名的安全性归约到标准SM2签名,由此证明我们所提协议的安全性,即如果原始SM2是概率多项式时间不可伪造的,那么我们的协议也满足概率多项式时间不可伪造性.最后,本文针对协议的正确性和性能完成了测试与评估.实验结果表明,在半诚实模型下,客户端计算量为4.381 ms,接近相同环境下客户端执行一次原始SM2签名的时间.特别地,协同签名未改变签名结果的格式以及签名验证算法,与标准SM2数字签名算法具有很高的兼容性,因此在实际应用中具有广泛的应用前景.

