ACT:可审计的机密交易方案
姜轶涵 李 勇 朱 岩
1(北京交通大学电子信息工程学院 北京 100044) 2(北京科技大学计算机与通信工程学院 北京 100083)
比特币是中本聪在2009年提出的分布式密码货币,其经过共识将交易信息(发送方、接收方、交易金额)打包公开存储在区块链上,因此可以不需要第三方中介而确认交易[1].在现代电子支付系统当中,用户必须信任银行不会篡改系统、不会滥用用户的隐私,而比特币采用化名地址给用户提供了隐私保护.由于交易是公开存储的,任何人都可以查看交易路径,并可以向前追溯到该比特币的起源.若交易与真实世界有关,则可能会追踪到用户真实身份,因此更多、更复杂的密码学技术被应用在区块链中以增强其隐私性.Zerocoin方案[2]通过非交互式零知识证明(non-interactive zero knowledge, NIZK)提供了发送方和接收方的不可关联性,Zerocash方案[3]运用ZK-SNARKs提供了匿名性程度极高的密码货币隐私保护方案[4],Monero方案[5]基于Crypto Note协议[6]、环状机密交易Ring CT[7]来隐藏交易金额和交易双方地址.然而,隐私保护程度的加强会带来另一个问题:缺乏和难以审计,可能会让地下钱庄洗钱、敲诈勒索等非法行为更加泛滥.文献[8]中的机密交易方案,利用Pedersen承诺可隐藏交易金额,审计方无法确知区块链中的交易情况,将导致网络洗钱等违法交易行为难以控制.而若将交易数据直接对审计方公开,又与用户隐私保护需求相悖,从而失去区块链本身的意义.
本文针对机密交易中过度强调隐私保护所导致的对区块链中的交易难以审计的问题,在保证用户交易数据隐私的同时,授权审计方获知某时间段内所有用户的交易总额,提出可审计的机密交易方案.
1 相关工作
对于区块链中隐私数据进行审计的尝试目前主要有2类方法:1)在交易确认中加入中心方;2)利用密码学工具.2016年英国央行和伦敦大学学院共同开发了数字货币框架RSCoin,由央行控制法定货币的发行,商业银行存储各交易账本,最终再由央行确认放入链中[9].央行对交易享有最终确认权,以此达到监管审计的目的.2017年Cecchetti等人提出了Solidus协议,该协议由若干个银行控制所有账户并代表用户完成交易[10].通过引入可公开验证的不经意RAM机为交易提供机密性.审计方通过2种方式进行审计:1)银行能够证明链上数据的正确性,审计方可以按需获取交易日志并验证其正确性和完整性;2)银行共享其私有解密密钥,审计方可以直接并主动监控银行及其账户内的活动.
在链中引入中心方干预交易的确认很难兼容现有带隐私保护的区块链应用,研究人员逐渐引入密码学工具以达到链外审计的目标.2016年,Garman等人扩展了Zerocash协议,通过引入追踪密钥追溯币的交易历史[11],为去中心化匿名支付提供追责功能.随后,Naganuma等人提出可审计的Zerocoin方案,发送者在交易生成中嵌入审计信息,允许指定审计方获得交易中的关联信息[12].以上2类方案都是对逐条交易进行审计,需要较大的审计成本;同时方案更改了交易结构,使交易尺寸增大,导致区块的传输性能降低.2018年,Narula等人提出即支持隐私保护又可审计的分布式账本zkLedger[13].zkLedger采用多栏总分类账结构,将银行间所有交易保存在一个账本上,一行代表一个交易,一列代表一个银行的所有交易.由交易发送方产生交易(一行),使用Pedersen承诺隐藏金额,而对于未参与交易的银行,发送方产生对金额值0的承诺,则可使交易参与方不被第三方知道[14].审计方通过账本中的一列对银行进行查询,得到一个银行的某些交易统计信息如交易和、均值等.zkLedger通过Schnorr型[15]非交互式零知识证明提供审计功能.与Zerocash方案不同,zkLedger方案不依赖可信第三方进行参数设置.与zkLedger粗粒度监管方式不同,Wüst等人提出了既支持隐私保护又可监管的密码货币方案PRCash[16],其监管粒度较细,针对的是各节点之间的交易.PRCash改进Mimblewimble方案来产生交易[17],每个输出均需要范围证明和监管证明,监管方作为第三方验证监管证明.PRCash方案监管的是交易额度,若超过限额,则通过监管证明解密部分信息获得接收方身份;若未超出限额,可通过监管证明验证其交易额在额度之内[14].但其只能监管到交易额的范围,如何设置一个通用的阈值进行监管是一个难点,若频繁采用小额度交易进行洗钱,可能会监管不当.2019年Li等人提出了可追溯的Monero方案[18].付款人在产生收款人一次性密钥对时,同时产生标签用于在收款人充当恶意付款人时追溯收款人的长期公钥.审计方通过使用自己的私钥解密标签中密文即可获得付款人的长期公钥,而通过对交易中的密文进行解密则可找到相应的一次性公钥,由此导致该方案的隐私性较弱.同年,Chen等人提出可审计追责的机密交易方案PGC[19],其将承诺形式的交易转换成Elgamal加密的形式,无需对随机数与金额保持追踪来获取信息;利用零知识证明确保其有效正确性;采用签名证明账户所有权.对于有争议的交易,PGC通过用户对该交易金额的正确性进行零知识证明来达到审计问责的目的.但该方案的研究限于理论层面,在实际应用中的性能有待考究.
2 系统框架
本方案中交易的创建过程类似机密交易,输入、输出形式均为对金额的Pedersen承诺,同时输入需要附带发送方地址.以图1为例介绍一个区块的结构,该区块中有2个交易:交易1为两输入单输出,同时附带一个范围证明range proof(Out1);交易2为单输入两输出,同时附带2个输出的聚合范围证明range proof(Out2,Out3).通过Bulletproofs生成聚合的范围证明,其具体构建见文献[20].

Fig. 1 Block structure图1 区块结构
该系统由3种角色组成:审计方、区块验证者(Leader)、用户.
1) 审计方.区块链外具有审计功能的参与方,可以查看所有区块以及审计多个区块中所有交易的和.
2) 区块验证者.审计方、用户相交互的媒介,设置为前一个区块的记账者,由共识协议(如PBFT共识)选出.
3) 用户.产生交易发送至区块链网络的参与方,分为发送方与接收方.
图2为例阐述审计过程[14]:
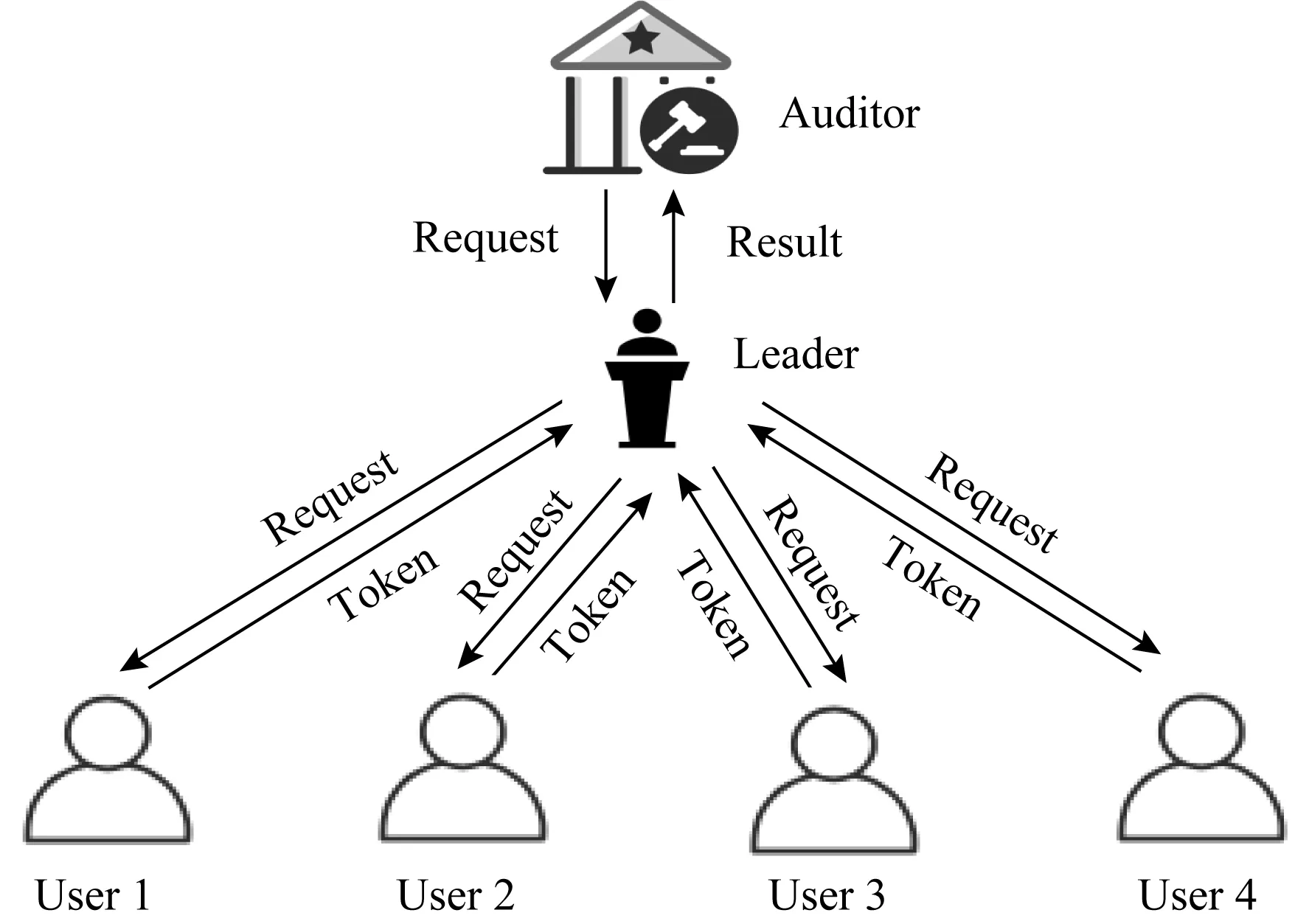
Fig. 2 Audit framework图2 审计框架
1) 审计方想审计区块链中多个区块中所有交易的和,先产生审计请求发送给上一个区块验证者;
2) 区块验证者收到请求后验证请求来源为审计方,则进行下一步与用户进行交互,否则为非法请求,丢弃该请求;
3) 区块验证者转发审计请求给各用户,每个用户验证收到的审计请求,验证通过后开始计算审计令牌;
4) 各用户将令牌发送给验证者,区块验证者根据令牌进行验证,将每个用户的结果计算、整合,得到最终结果发送给审计方;
5) 审计方将收到的结果解密得到所有交易的总和,并验证其正确性.
3 ACT方案和安全模型定义
3.1 可审计机密交易方案(ACT)定义
ACT(auditable confidential transaction)方案由(Setup,Request,Verify_Request,Response,LDec,Add,Audit,Verify)8个算法组成[14]:
1)Setup(1λ)→(pubpara,secpara).参数生成算法,输入安全参数λ,输出公共参数pubpara、私有参数secpara.
2)Request(pubpara,req,ssk)→(req,sig).请求算法,由审计方执行,输入公共参数pubpara、请求消息req与签名私钥ssk,输出审计请求req及签名sig.
3)Verify_Request(pubpara,req,sig)→{0,1}.验证请求算法,由验证者和用户执行,输入公共参数pubpara、审计请求req、签名sig,输出1代表审计请求验证通过,可以进行后续步骤,0表示审计请求非法,丢弃该请求.
4)Response(pubpara,si,sri)→(Tokeni).响应算法,由用户i执行,输入公共参数pubpara、用户i的交易和si、随机数之和sri,输出用户i的审计令牌Tokeni.
5)LDec(pubpara,secpara,Tokeni)→(ci,msri).解密算法,由验证者执行,输入公共参数pubpara、secpara、审计令牌Tokeni,输出每个用户的交易和的密文ci以及每个用户的随机数和msri.
6)Add(pubpara,ci,msri)→(audit_data).求和算法,验证者输入公共参数pubpara、每个用户交易和的密文ci、每个用户的随机数和msri,输出审计数据audit_data.
7)Audit(pubpara,ask,audit_data)→sum.审计算法,审计方输入公共参数pubpara、审计私钥ask、审计数据audit_data,输出交易和sum.
8)Verify(pubpara,sum,audit_data)→{0,1}.验证算法,审计方输入公共参数pubpara、上一步算法产生的交易和sum、审计数据audit_data,输出0或1.1表示审计结果正确,用户和验证者均诚实;0表示验证者不诚实.
3.2 安全模型定义
本节介绍ACT方案所满足的安全性质,分别为可审计性、审计可靠性以及交易金额隐私性[14].
定义1.可审计性.对于ACT方案,如果满足如下条件,则审计方可以审计到所有用户的交易总额.
Verify(pubpara,sum,audit_data)=1]≥1-v(λ),
其中,υ(λ)为可忽略函数.
即对于诚实按照操作进行交互的用户和验证者,审计方可以正确审计到一段时间内该网络总的交易额.
定义2.审计可靠性.对于ACT方案,如果满足条件,则该方案具有审计可靠性.
Verify(pubpara,sum,audit_data)=0]≥1-v(λ),
其中,RD指真实数据,∉RD表示伪造的数据,enc_sum表示所有用户交易总和的密文.即审计方可以检测到伪造数据,假数据无法通过审计验证.
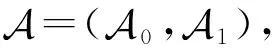

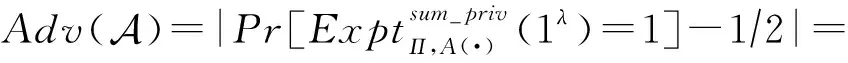
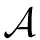
4 ACT方案设计
ACT方案基本设计思想如下:利用数字签名算法生成审计请求,确保只有审计方有权审计.用户对个人交易总额进行双重加密生成审计令牌:第1重加密采用同态加密,使得审计方和区块验证者无法获知各用户各自的交易和;第2重加密附带零知识证明,可检测不诚实用户伪造数据,同时保证交易数据隐私和审计数据准确性.审计令牌包含交易输入承诺中的随机数总和以及零知识证明.区块验证者根据令牌解密外层密文,验证零知识证明有效性;随后将各用户的内层密文相乘、以及将随机数的和相加,同时发给审计方.审计方解密得到所有用户的交易额总和,并利用Pedersen承诺的同态性可验证其正确性.
4.1 ACT方案具体构建
ACT方案具体构造为:
1)Setup(1λ)→(apk,ask,lpk,lsk,spk,ssk).输入安全参数λ,产生审计方公钥apk=(N,g1),私钥ask=μ;验证者私钥为lsk,公钥lpk=(f,g2),Elgamal加密体制模数k以及审计方签名私钥ssk,签名公钥spk.输出pubpara=(k,apk,lpk,spk),secpara=(ask,lsk,ssk).
2)Request(pubpara,req,ssk)→(req,sig).请求信息req=(h_first,h_end)表示审计区块高度从h_first到h_end的区块交易和;对req生成数字签名,签名记作sig=(Ω,s),输出审计请求req和签名sig.
3)Verify_Request(pubpara,req,(Ω,s))→{0,1}.验证签名sig,输出1代表审计请求验证通过,可以进行后续步骤,0表示审计请求非法,丢弃该请求.
4)Response(pubpara,si,sri)→(csumi,π1i,sri,csri,π2i).对于交易总额进行双重加密及证明,具体过程由3步组成:
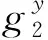
π1i=NIZK{Enc(lpk,hsri)明文是hsri∧公钥为lpk};

输出Token=(csumi,sri,csri,π1i,π2i).
5)LDec(pubpara,secpara,csumi,sri,csri,π1i,π2i)→(ci,msri).验证者验证π1i,π2i的有效性后,将csumi和csri进行解密.csumi的明文ci=cp2(cp1lsk)-1modk,csri的明文msri=ct2(ct1lsk)-1modk,计算hsri是否等于msri,相等则证明用户诚实,所发随机数之和数据正确.

7)Audit(pubpara,ask,enc_sum)→sum.审计方利用私钥ask=μ将验证者发来的密文enc_sum进行解密,得到交易和sum=Dec[enc_sum]=L(enc_sumμmodN2)L(gμmodN2) modN,其中L(x)=(x-1)N.
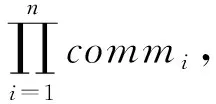
4.2 零知识证明的构建
以NIZK-π1i为例展示响应算法Response(pubpara,si,sri)→(csumi,π1i,sri,csri,π2i)中零知识证明的具体构建.NIZK-π1i=NIZK{Enc(lpk,hsri)中明文是hsri且公钥为lpk},即证明用户发给验证者的随机数之和sri正确,与承诺中对应随机数之和相匹配.设群G=f=g=h,公钥lpk=flsk,A,B,C∈G,用户(证明者)使得验证者相信他知道使得A=fx,B=
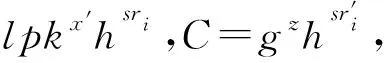
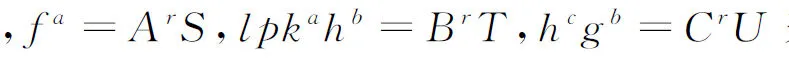
5 安全性分析
本节对ACT方案的安全性进行证明.
定理1.在用户和验证者都是诚实的前提下,审计方能够审计到一段时间内所有交易的总消费额.
证明. 假设用户和验证者均诚实,则审计方收到的数据信息是正确的.审计方收到enc_sum后,根据Pailliar加密同态性,
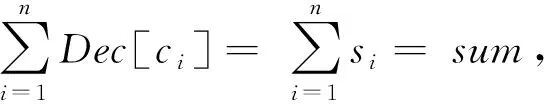
证毕.
定理2.如果零知识证明满足可靠性,且承诺方案满足绑定性,则ACT方案满足审计可靠性.
证明. 可靠性指若审计方收到虚假数据,则其通过验证算法的可能性极小.虚假数据来源于2方面:①用户;②验证者.
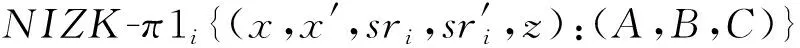
情况2.假设存在不诚实的验证者对审计方进行欺骗,即在Add(ci,msri)→(enc_sum,r_sum)算法产生输出后,编造假数据通过审计方验证的概率不可忽略,则存在enc_sum′≠enc_sum,r_sum≠r_sum′,使得Pr{Dec[enc_sum′]=sum′:gsum′hr_sum′=gsumhr_sum}≥1-v(λ),v(λ)为可忽略函数.与承诺方案的绑定性相矛盾,所以不诚实的验证者无法欺骗审计方.综上,该方案具有可靠性.
证毕.
定理3.如果零知识证明是零知识的,且判定复合剩余问题是困难的,则该方案满足交易金额隐私性.
证明. 通过游戏序列来证明本定理.
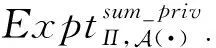
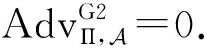
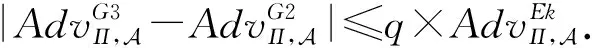
证毕.
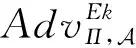
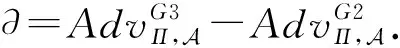
证毕.
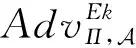
证明. 考虑图5所示的区分算法D:

c=(1+N)sb×rNmodN2.
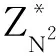
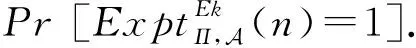
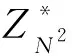
Pr[D(N,r)=1]=12.
因此,
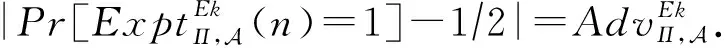
由判定复合剩余假设,可得:
|Pr[D(N,[rNmodN2])=1]-
Pr[D(N,r)=1]|≤v(λ).
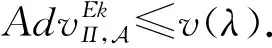
因此,如果零知识证明是计算零知识的,且判定复合剩余问题是困难的,则该方案满足交易金额隐私性.
证毕.
6 性能分析
本节通过仿真实验对交易中范围证明与审计中各算法进行性能评估.实验环境配置为Mac OS操作系统,8 GB RAM,CPU为Intel Core i5 2.3 GHz.实验程序采用C语言编写,调用pbc,libsecp256k1等密码学库进行双线性映射、点乘等运算.如图6、图7所示为PRCash与Bulletproofs范围证明的生成与验证时间对比,PRCash范围证明采用的是文献[23]中基为4的证明形式,由于其采用了效率较低的双线性映射,因此时间较长,随着范围的增加,使用Bulletproofs生成证明的效率可以提高3倍以上,而验证效率则可以提高8倍以上.
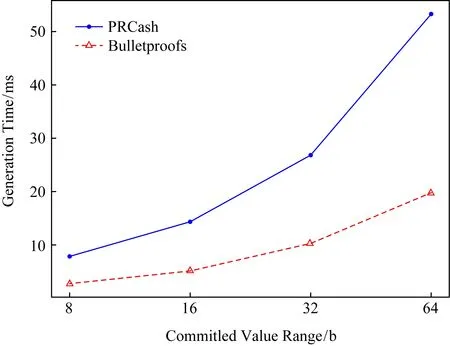
Fig. 6 Generation time for range proof图6 范围证明生成时间
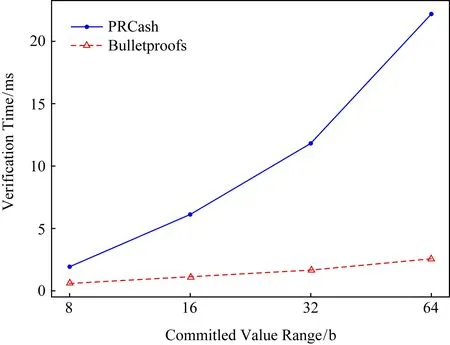
Fig. 7 Verification time for range proof图7 范围证明验证时间
图8所示为ACT方案中各算法在不同密钥长度下的执行时间折线图.实验中对Paillier密码体制中的N分别应用了4种长度:512 b,1 024 b,2 048 b,3 072 b,在4种长度下模拟得到了Response(分为encrypt与NIZK两步)、LDec(分为decrypt与NIZK两步)、Audit算法的执行时间.结果显示,算法中NIZK的生成时间约为加密的2倍,而验证者验证NIZK的时间则达到解密的10倍左右,占据了算法执行的大部分时间.在2 048 b下,用户生成审计令牌的时间大约需要0.66 s,验证者对于一个用户发来的一个响应执行LDec算法大约需要0.6×2=1.2 s,若用户数为100个,则每次审计时验证者需要大约2 min.
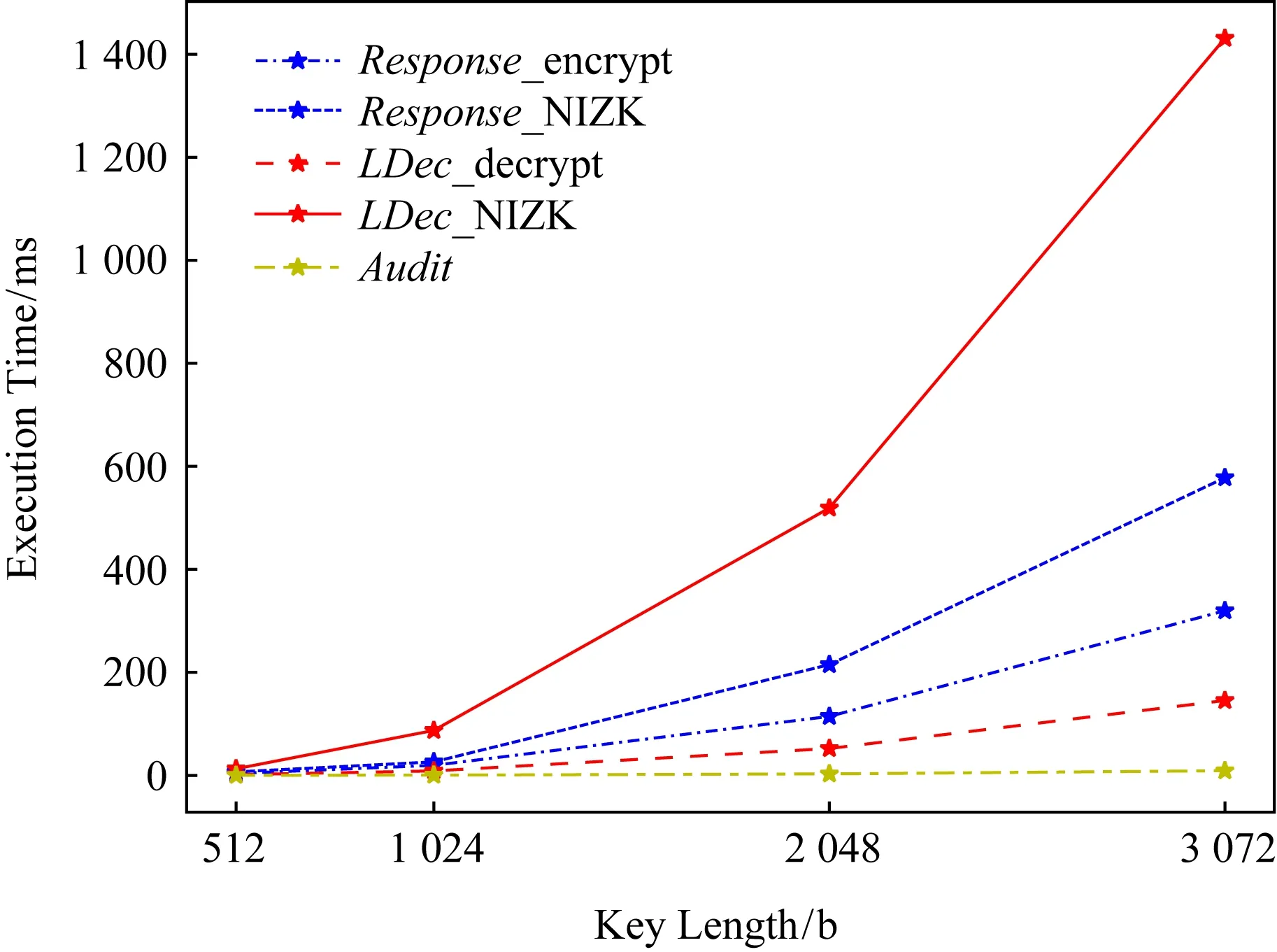
Fig. 8 Execution time for ACT algorithm图8 ACT算法的执行时间
图9所示为交易个数在10万~100万时审计方执行Verify算法的时间.实验中模拟单个交易金额均为100密码币,由于运行Verify算法需要将审计的区块内所有交易输入承诺相乘,因此图9中实线显示交易数越多,算法执行时间越长.若采取预先计算的形式,将交易乘积缓存,则审计时无需做大量的乘法运算,如图9中虚线所示,采用缓存形式的算法执行时间基本独立于交易个数,且时间很短,约为3 ms.
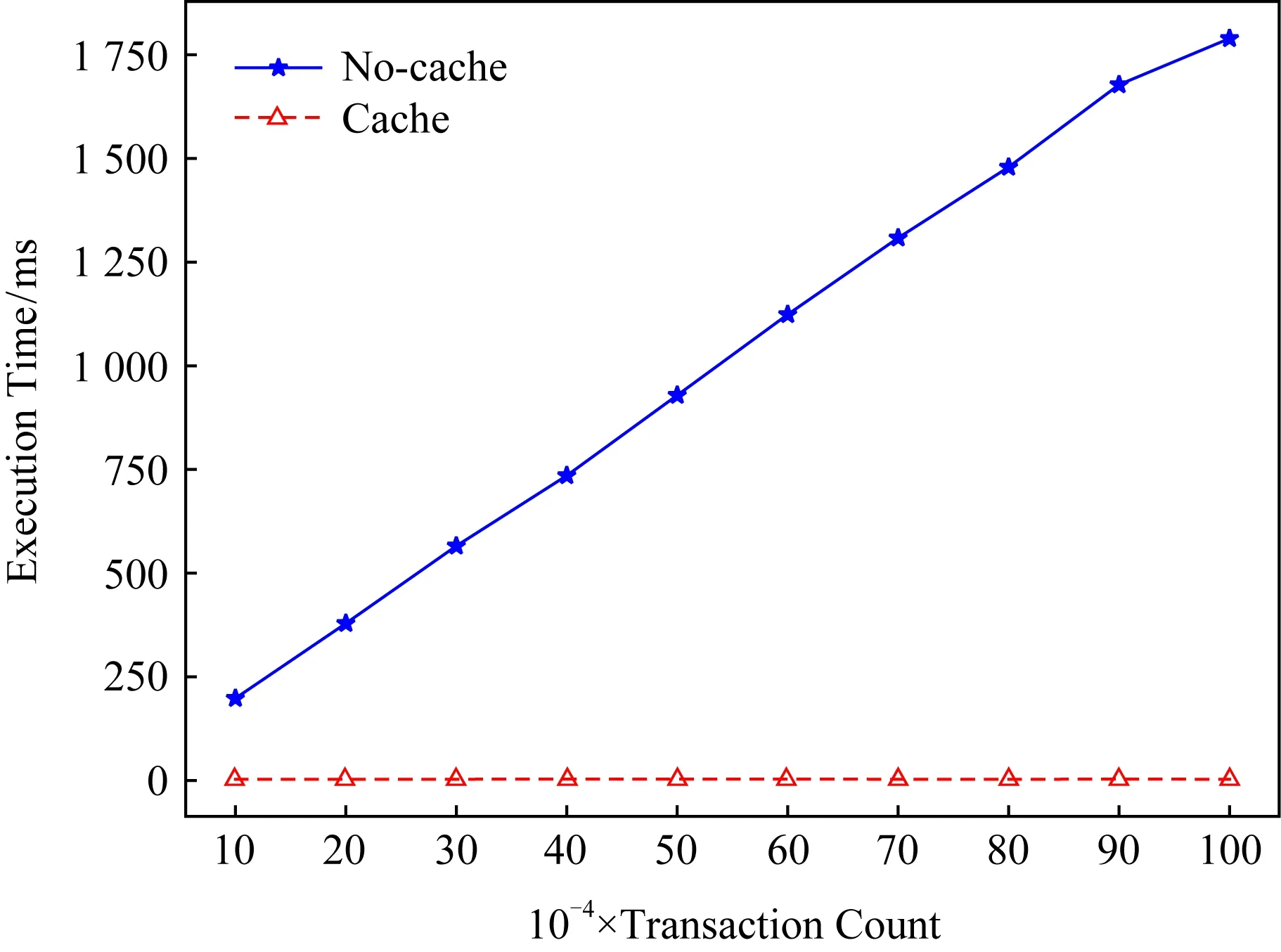
Fig. 9 Execution time for Verify algorithm图9 运行Verify算法的执行时间
7 总 结
针对机密交易金额隐私性强导致审计缺失和审计困难的问题,本文提出可审计交易总额的机密交易方案ACT,利用签名对审计请求来源进行身份认证,确保审计方的合法身份.该方案在审计中引入Paillier同态加密,可以保护单个交易以及单个用户的金额隐私,同时采用零知识证明在保证交易隐私性的同时可有效检测到不诚实用户伪造数据,从而保障审计数据的准确性.通过安全性分析及性能分析,该方案可以实现一段时间内区块链网络中交易总额的审计,同时可以有效保护交易金额隐私.且交易创建过程中利用Bulletproofs范围证明技术,使得交易创建与验证的效率提高.应指出:由于交易和范围有限,当交易和较小时,验证者有可能通过穷举获取到单个用户的交易和,可通过调整审计区块范围提高金额总和,从而增加验证者通过穷举获知用户交易和的时间成本.同时计算审计令牌时涉及的零知识证明占据了大部分时间,因此如何进一步优化审计策略、提高审计效率是下一步研究的方向.
致谢感谢审稿专家的宝贵意见让本文更完善,比如指出验证者可能穷举获得单个用户的交易和问题.

