循环安全的同态加密方案
赵秀凤 付 雨 宋巍涛
(信息工程大学密码工程学院 郑州 450001)
当今世界,大数据、云计算等蓬勃发展,使互联网时代迈上一个新台阶.然而,云计算和大数据所具有的数据集中、资源共享、高度互联、全面开放等特点,一方面打破了传统IT领域的信息孤岛,另一方面也带来了更严峻的安全问题.云计算模式的核心是数据,本质是服务,特点是“零信任”,因此,“数据在不可信环境下的安全计算(服务)”成为解决云计算安全的一个关键问题.2009年IBM实验室的Gentry首次给出了“全同态加密”(fully homomor-phic encryption, FHE)方案[1-2].全同态加密可以在不解密的情况下对密态数据进行各种运算,其结果在解密后与对明文进行相应运算的结果是一样的.全同态加密不仅能够对密文进行任意的盲操作,而且还能够对计算操作行为本身进行加密的密码算法,因此,全同态加密真正从根本上解决了将数据及操作委托给第三方时的保密问题,使人们既可以充分利用云计算强大的计算和存储能力为用户提供海量密文处理服务,又可以自己管理保证数据安全的密钥,实现了“数据在不可信环境下安全计算(服务)”.
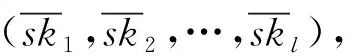
本文的主要贡献包括2个方面:
1) 给出了满足循环安全性的公钥同态加密方案,并给出了安全性证明和参数设置分析;
2) 通过引入拒绝采样技术,对上述满足循环安全性的同态加密方案进行了优化,将方案参数从超多项式级降低到多项式级,大大约减了参数规模,有效提升了方案的效率.
1 相关工作
关于循环安全的加密方案已有一些研究成果.Boneh等人基于无随机Oracle的DDH假设构造了一个循环安全的公钥加密方案[3].Applebaum等人根据基于错误学习(learning with error, LWE)问题的Regev加密方案[4],构造了循环安全的有效密码体制[5].在循环安全的同态加密方面,杨晓元等人[6]基于LWE问题的变形给出了一个对私钥的线性函数满足循环安全的FHE方案,但是这个困难假设并不是一个标准的困难假设.Zhao等人[7]给出了矩阵GSW方案[8]满足循环安全性的一个充分条件,但是缺乏必要性证明.2011年美国密码学年会,Brakerski和Vaikuntanathan[9]基于环LWE问题给出了一个循环安全的同态加密方案,称为BV方案.BV方案实现循环安全性的基本思路是利用“噪声淹没技术”(noise flooding technique),即在原加密方案的基础上,再引入一个“宽高斯”分布的噪声,从而使得对密钥加密的密文与对普通明文加密的密文不可区分.由高斯分布的叠加性和不可区分性,保证挑战者模拟私钥的密文.
本文给出的循环安全的公钥同态加密方案,通过引入拒绝采样技术有效约减了密文模的规模,提升了同态运算的效率.该研究成果可以为同态加密方案设计与实现提供理论参考.
2 基础知识
本节主要介绍本文用到的基本定义和重要的引理.
2.1 离散高斯分布
标准方差为σ、中心为c的高斯分布定义为
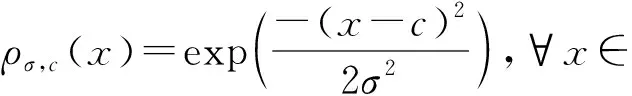
对于∀x,c∈Rn,离散高斯的分布概率密文函数定义为
Z和Zn上的离散高斯分别定义为


引理3[12].令n∈N,m=2n,f(x)=xn+1,令R=Z[x](f(x)).对于任意的s,t∈R,
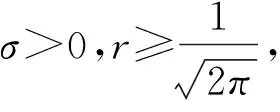
特别地,当n=1,r=6时,有:
引理5[14].令λ为安全参数.Φm(x)=xn+1是度为n=φ(m)=m2的m次分圆多项式.令σ≥为一个实数,q≡1(modm)为素数.令R=Z[x]Φm(x),则存在一个从2ω(log n)×(qσ)-近似R-SVP问题到RLWEΦm,q,χ的随机归约算法,其中,χ=DZn,σ为离散高斯分布.归约算法的运行时间为poly(n,q).
2.2 拒绝采样
拒绝采样技术由Neumann提出,给出了通过源概率分布采样得到目标概率分布采样的一个方法[15].PKC2008,Lyubashevsky利用拒绝采样构造了基于格的身份识别协议[16].Crypt2013,Ducas等人利用拒绝采样构造了基于格的BLISS数字签名算法[17].NIST征集的多数后量子数字签名候选算法也采用了拒绝采样技术.
引理6.拒绝采样.令V是任意一个集合,h:V→R和f:Zm→R为概率分布.若gv是以v为索引的一簇概率分布,并且存在一个M∈R,使得:
∀v∈V,∀z∈Zm,M.gv(z)≥f(z),
那么,2个算法输出的分布是相同的:
1)v←h,z←gv,以概率f(z)(M.gv(z))输出(z,v);
2)v←h,z←f,以概率1M输出(z,v).
2.3 同态加密的循环安全性定义
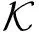
1) 挑战者计算(pk,sk,evk)←KeyGen(λ),并随机选择一位b←{0,1};



在基于LWE的FHE方案中,Evalevk(f+,Encpk(0),f(sk))可以视为加密f(sk)的密文.
3 循环安全的公钥同态加密方案
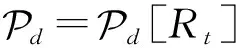
为了实现对私钥sk的多项式p(sk)的KDM安全性,我们利用对称版本的方法,将标准的同态加密的密文(c0,c1)扩展为(c0,c1,…,cd),其中d为多项式p(sk)的度.我们令d=2,即我们考虑对私钥sk的平方函数满足循环安全性的同态加密方案,记作KDM.PKHE.
3.1 方案描述
具体算法描述为:
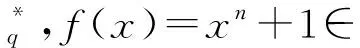
2) KDM.PKHE.Keygen(1λ).随机选择a0∈Rq,从离散高斯分布采样得到s,e0←DZn,σ,计算b0=a0s+te0,输出私钥sk=s和公钥pk=(a0,b0).
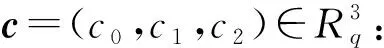
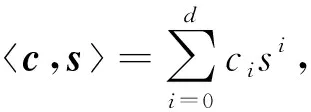
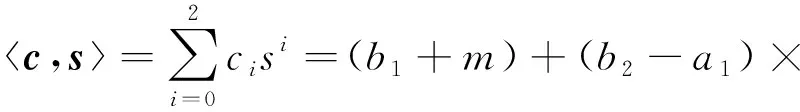
故上述无穷范数小于q2时,则可以解密成功.
3.2 循环安全性证明
为了给出KDM.PKHE方案的循环安全性证明,我们首先证明引理:
引理7.设ξ和η是Zq上2个独立的随机变量,且ξ在Zq上服从均匀分布,那么ξ+η在Zq上也服从均匀分布.
证明. 设ξ和η独立,则∀z∈Zq,有:
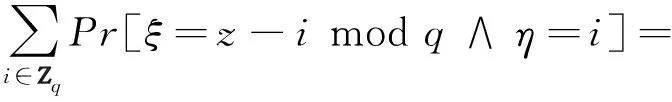
由ξ在Zq上服从均匀分布知:
因此有:
即ξ+η在Zq上服从均匀分布.
证毕.
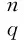
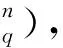
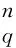
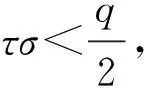
证毕.
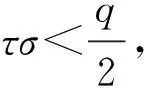
实验G0. 实验G0是真实的KDM-CPA安全实验,如2.3节定义中所述.在该实验中,挑战者按照加密算法生成挑战密文
实验G1. 除了挑战密文的生成方式不同之外,实验G1和G0相同.实验G1中,挑战者按照2种方式生成f(sk)的挑战密文:
当b=0时,设置挑战密文为
当b=1时,设置挑战密文为
(c0=b1+0,c1=b2-a1,c2=-a2).
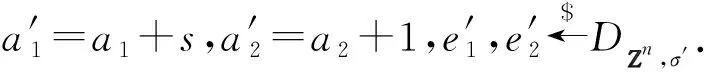
证毕.
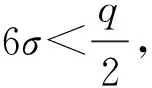

(1)
证明. 对于消息s2∈Rt,考察同态加密方案的密文c0:
(2)
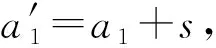

令Δ=2n1.5σ2,由σ′=2ω(log n)σ2,有:
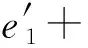
另外,考察同态加密方案的密文c1:
(3)
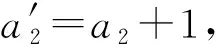

因此,敌手区分实验G1和G0的概率是忽略的,引理8成立.
实验G2:除了挑战密文的生成方式不同之外,实验G2和G2相同.实验G2中,挑战者按照2种方式生成f(sk)的挑战密文:
当b=0时,设置挑战密文为
当b=1时,设置挑战密文为
(c0=b1+0,c1=b2-a1,c2=-a2).
其中,ui(i=0,1,2)为环Rq中的随机元素.
证毕.
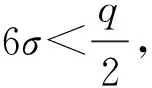
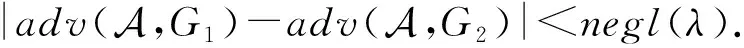
(4)
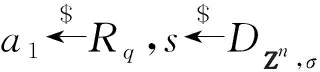
综上,有:
由于在实验G2中,挑战密文是与私钥s独立的均匀随机的环元素,因此敌手的优势是可忽略的,即:
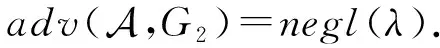
(5)
综合式(1)(4)(5),有:
至此,我们证明了敌手的KDM安全性实验中的优势是可忽略的.
证毕.
3.3 参数设置
KDM.PKHE方案中的参数并不是独立选择的,相互之间存在一些制约关系,下面给出详细分析.
1) 为了使得离散高斯分布DZn,σ′可以“淹没”DZn,σ上采样的2次多项式,要求σ′=2ω(log n)σ2.

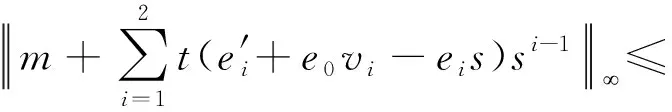
故密文模q满足q>t×2ω(log n)×σ2可保证解密正确性.
4 改进方案
为了利用噪声淹没技术实现循环安全性,离散高斯分布DZn,σ′的标准方差σ′需要满足σ′=2ω(log n)σ2,而解密正确性要求模数q>t×2ω(log n)×σ2,因此,模数q是n的超多项式函数,使得KDM.PKHE方案的效率极低.下面,我们以d=2这种情况为例,通过引入拒绝采样技术来约减σ′的规模,进而降低q的规模,并最终提高循环安全的KDM.PKHE方案效率.
4.1 方案描述
除了加密算法中噪声采样算法不同之外,改进方案同KDM.PKHE方案基本相同,记为RS.KDM.PKHE.
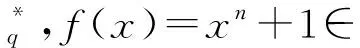
2) RS.KDM.PKHE.Keygen(1λ).随机选择a0∈Rq,从离散高斯分布采样得到s,e0←DZn,σ,计算b0=a0s+te0,输出私钥sk=s和钥pk=(a0,b0).

① 计算ai=a0vi+tei,其中vi,ei←DZn,σ.
③ 计算对m加密后的密文:
c0=b1+m;
c1=b2-a1;
c2=-a2.
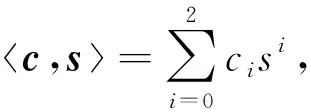
4.2 方案正确性分析
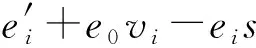
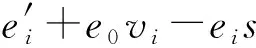
如图1所示(n=1的情形),我们令拒绝采样的目标概率分布是DZn,σ′,源概率分布是DZn,σ′,Ei.为了利用拒绝采样技术,我们需要找到实数M,使得对于所有的x∈Zn,有DZn,σ′(x)≤M×DZn,σ′,Ei(x).根据高斯分布的定义有:
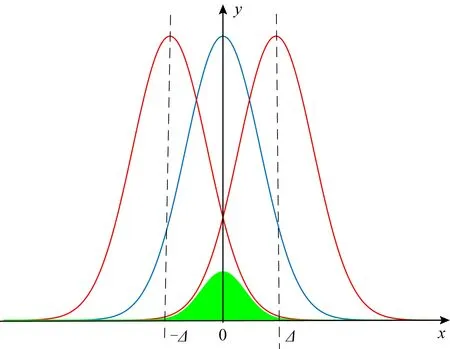
Fig. 1 Reject sampling technique图1 拒绝采样技术
4.3 方案性能分析
通过第2节分析可知,只要设置σ′=τ×Δ=2τn1.5σ2,即可以利用拒绝采样技术完成加密过程.如表1所示,RS.KDM.PKHE方案中σ′从BV的KDM.SKHE和KDM.PKHE方案中σ2的超多项式倍2ω(log n)×σ2降低为σ2的多项式倍poly(n)×σ2,大大约减了的σ′的规模.根据解密正确性要求,密文模数q的规模从2ω(log n)×σ2×t降低到poly(n)×σ2×t,有效约减了密文规模,提升了同态运算的效率.
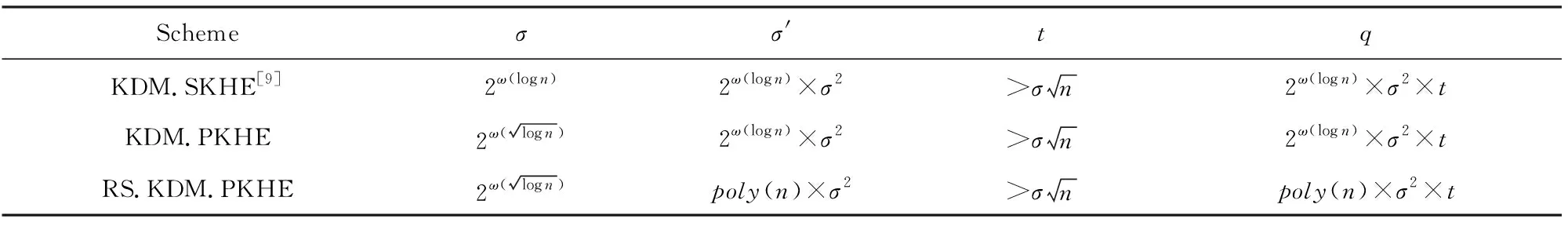
Table 1 Parameter Setting表1 参数设置
4.4 循环安全的公钥同态加密方案
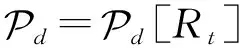
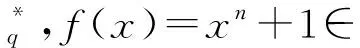
2) KDM.KeyGen(1λ).随机选择a0∈Rq,从离散高斯分布采样得到s,e0←DZn,σ,计算b0=a0s+te0,输出私钥sk=s和公钥pk=(a0,b0).
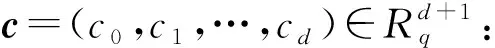
① 计算ai=a0vi+tei,其中vi,ei←DZn,σ.
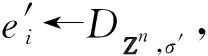
③ 计算对m加密后的密文:
c0=b1+m,
ci=bi+1-ai,i=1,2,…,d-1,
cd=-ad.
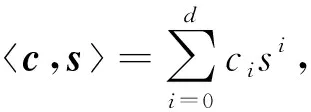
m=c,smodt.
5 结束语
本文基于噪声淹没技术给出了循环安全的公钥同态加密方案,并给出了安全性证明和参数设置.进一步,首次将拒绝采样技术引入到循环安全的同态加密方案构造方法中,给出了优化的循环安全公钥加密方案,使得系统参数从超多项式级降低到多项式级,有效约减了公钥规模和密文规模.
另一方面,由于拒绝采样技术的应用,导致加密算法的计算复杂性增加,但是考虑到同态加密方案的瓶颈在于密文运算,而不是新鲜密文的生成算法,而我们的方案将密文规模从超多项式级降低到多项式级,因此,可以有效降低密文运算的计算复杂性.总体而言,基于拒绝采样技术构造的循环安全性同态加密方案具有良好的性能.

