基于Matlab 的标枪形心位置研究
陈 瑞,苏小珂,肖人峰,田才艳,张 斌
(成都信息工程大学 通信工程学院,四川 成都610000)
1 引言
在标枪运动中,标枪投掷距离的大小分别受运动员能力、标枪的技术参数和比赛环境三方面因素的影响[1]。其中运动员能力包括出手速度、出手角、初始攻角、出手高度、出手时标枪的初始俯仰角速度等,标枪的参数有长度、质量、几何形状、重心的位置、形心的位置等,环境因素有空气的密度与粘度、风力、风向等[2]。在本问题中,为了简化讨论作出了如下假设:运动员出手高度为2 m,标枪质量为800 g,不考虑标枪在飞行过程中的进动影响,空气密度为1.184×10-3g/cm3,空气粘度为1.84×10-5Pa·s[3]。
2 模型1 的建立与求解
根据题目所提供的标枪基础数据,求出标枪沿标枪中轴线剖面面积、标枪表面积和标枪形心的位置。使用MATLAB、相关数学以及物理知识进行求解。步骤如下:根据标枪基础信息,使用MATLAB 将标枪外轮廓画出;将标枪进行分段拟合;使用一重积分求出标枪沿标枪中轴线剖面面积;使用旋转曲面求积分求出标枪的表面积;通过多边形形心公式求出形心位置。
2.1 标枪外轮廓图的绘制
通过MATLAB 的绘图功能将附件所给的标枪基础数据绘制成标枪的外轮廓。
2.2 标枪分段拟合
将标枪分为6 段,如表1 所示。
各段拟合函数f(x)如下所示:
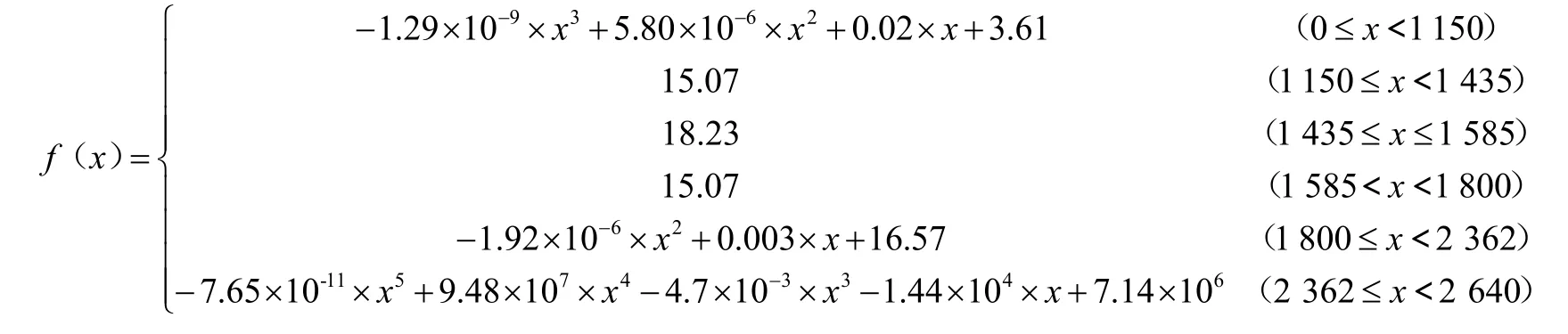

表1 标枪分段
2.3 求解沿标枪中轴线剖面面积
沿标枪中轴线剖面即为标枪外轮廓,所以通过计算一重积分的方法来计算外轮廓的面积,也就是沿标枪中轴线剖面面积。
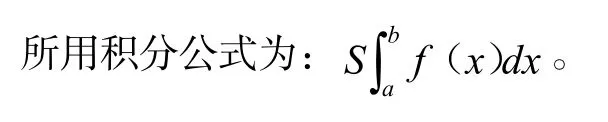
使用MATLAB求解公式求得剖面面积为S1=0.064 6 m2。
2.4 求解标枪表面积
若想求出标枪表面积可以通过高数中求解旋转面积分算法。
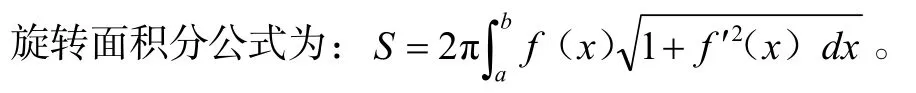
使用MATLAB求解公式所求标枪表面积S2=0.201 2 m2。
2.5 求解标枪形心的位置
使用多边形的形心公式可以较为简便地得出形心的位置剖面面积为:
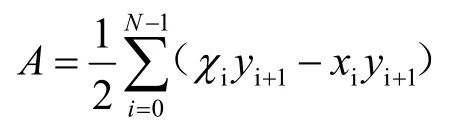
剖面的形心由下式给出:

本文使用MATLAB 软件将公式实现,最终得出标枪形心的位置。
3 模型2 的建立与求解
3.1 多元线性回归方程的假设
由于投掷距离受多个因素的影响,在剔除无效点后,假设投掷距离y与出手速度x1、出手角度x2、初始攻角x3具有如下关系:
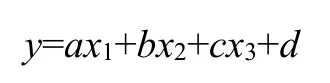
3.2 多元线性回归方程系数的计算

3.3 回归方程的检验
对此模型拟合的P值进行计算,此拟合结果为P=6.299×10-16,P<<0.000 1,说明本次拟合有效。
对此模型拟合的R相关系数进行计算,R=0.979 8≈1,接近1,置信度很高。
对此模型F值进行检验,F=307.803 1,F值越大,越能说明y与xi之间具有线性关系。
综合上述三点可证明,多元线性回归方程的假设成立。
3.4 偏回归平方和Qi的比较
由于利用偏回归平方和Qi可以衡量每个变量在回归中所起的作用大小(即影响程度),设S回是p个变量所引起的回归平方和,S回1是p-1 个变量所引起的回归平方和(即除 去xi),则偏回归平方 和Qi为Qi=S回-S回1=即去掉变量xi后,回归平方和减少的量。
最终得出出手速度x1对投掷距离y的影响最大,且影响效果很强,出手角度x2也对投掷距离y有影响,但影响效果相对较弱,初始攻角x3对投掷距离y的影响相对最弱。

